不同圍壓下花崗巖三軸壓縮疲勞特性試驗
黃正均, 趙星光, 張 磊
(1. 北京科技大學 土木與資源工程學院, 北京 100083; 2. 核工業北京地質研究院, 北京 100029)
0 引 言
巖石疲勞是指巖石在循環載荷反復作用下,其力學性能和變形行為的演化發展過程。在礦山、土木、交通等巖土工程中,通常會遇到巖石的“疲勞損傷”問題。然而,巖石在循環載荷作用下的性能明顯不同于靜態單調載荷。因此,研究巖石的疲勞特性與破壞機理,對巖體地下工程設計施工與長期穩定性評價等具有重要指導意義[1-2]。
目前,大家普遍認為巖石壓縮條件下的疲勞特性取決于所施加的應力水平、振幅、加載頻率、波形、圍壓等因素。文獻[3-5]中分析了巖石的疲勞損傷過程,研究了模量、變形、聲發射特征等發展規律及其關系。文獻[6-8]中分析了砂巖循環加載試驗,得出了疲勞壽命與應力幅值、軸向應變、加載波形等的關系。文獻[9-10]通過分析砂巖單、三軸下的疲勞特性,揭示了加載頻率、圍壓和振幅對巖石疲勞強度、軸向剛度等特性的影響。文獻[11-15]中從微細觀角度分析了花崗巖在疲勞階段的裂紋擴展特征,提出了一種“倒S型”損傷模型來描述巖石的非線性疲勞損傷過程。
上述研究成果大多主要針對砂巖、大理巖等硬脆性指數不高的巖石,而對花崗巖等結晶類巖石的研究較少,尤其是在圍壓條件下受動態循環載荷作用的疲勞特性研究更是鮮見。本文針對花崗巖進行了圍壓條件下動態三軸循環加卸載試驗,研究花崗巖等硬脆性指數較高的結晶類巖石的疲勞試驗方法及其演化特性,并分析不同圍壓條件對其疲勞損傷過程的影響。
1 試驗樣品與設備
1.1 巖石樣品
試驗采用花崗巖樣9件(BS18-1~BS18-9,見圖1),取自甘肅北山地區,被認為是中國高放廢物處置最適合的地區之一。巖樣被地質定名為細粒狀二長花崗巖,塊體密度為2.642 g/cm3,縱波波速約為4.2 km/s,尺寸規格均為φ50 mm×100 mm圓柱體。樣品垂直度和端面平整度公差均滿足ASTM、ISRM等建議和規定的試驗方法,以及國內《工程巖體試驗方法標準》等標準要求。

圖1 巖樣照片(BS18-1)
1.2 試驗設備及參數
試驗采用美國MTS公司制造的815系列巖石力學測試系統完成(見圖2)。主要功能參數包括:軸向最大可施加載荷2 700 kN;可提供最大圍壓140 MPa;振動頻率0.01~5 Hz;可產生三角波、正弦波、斜波、方波,組合波和隨機波等波形。同時,為記錄試驗過程中巖樣的變形曲線,采用了一對軸向和橫向引伸計進行變形測量,如圖3所示。其軸向最大量程為5 mm,環向量程為-2.5~8 mm。

圖2 MTS 815巖石力學測試系統

圖3 軸向和橫向變形測量引伸計
2 試驗方法與過程控制
2.1 試驗方案設計
本文目的在于通過動態三軸循環加載試驗,研究花崗巖在不同圍壓下的疲勞特性和演化規律。因此,試驗方案設計為固定頻率,但變化圍壓(0~15 MPa不等);同時,考慮圍壓對巖石壓縮強度的影響,加卸載振幅設置為動態值,即固定所有試樣加卸載下限荷載水平為20 kN,上限荷載水平隨圍壓變化而變化。
先通過手動控制方式,以0.1 MPa/s的加載速率施加圍壓至預設值。接著以軸向載荷的控制方式進行軸向靜態單調加載,速率為1 kN/s,并在加載過程中實時監測軸向應力-體積應變曲線。當體積應變曲線出現拐點,即載荷達到裂隙損傷應力點σcd時(裂隙損傷應力點,為巖石強度的一個臨界應力點),切換控制方式為橫向變形控制加載,速率為25 μm/min。繼續加載至巖樣達到預設目標體積應變量時,即開始進行動態循環加卸載。采用頻率1 Hz、正弦波形載荷控制方式進行,直到試樣破壞,加載路徑如圖4所示,圖中:σ1-σ3為軸向主應力差;σa、σb、σc為疲勞起始點軸向應力;σcd為裂隙初始點應力;εv為體積應變;t為時間。。
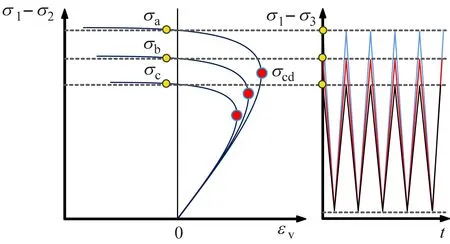
圖4 疲勞加卸載試驗方案設計
2.2 試驗過程及控制
所有巖樣在試驗前均用熱縮管進行密封處理,同時試樣兩端涂抹一層薄的潤滑劑以消除壓縮過程中的端部效應。整個試驗過程中通過一套軸向和橫向引伸計進行應變測量(見圖5),并將體積應變值作為外部參數設置進站臺程序,以便于實時監測應力-體積應變曲線。所有試驗均通過MPT程序控制進行,試驗前根據設計方案設置試驗步驟,然后自動運行試驗程序,并通過實時曲線監測窗口,觀察巖樣應力-應變曲線,防止意外情況發生,如圖6所示。

圖5 試樣安裝照片
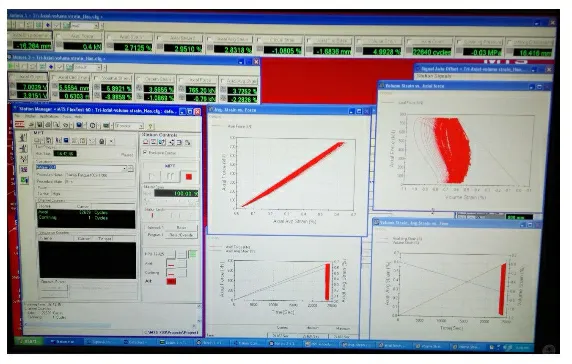
圖6 試驗過程控制和監測窗口
3 試驗結果及分析
3.1 試驗結果
根據前述試驗方案,共對9件巖樣進行了不同圍壓條件下的動態循環加卸載試驗,圖7為部分試樣的典型應力-應變曲線。全部巖樣的試驗結果如表1所示。從表1可知,圍壓值從1.5~12.5 MPa共7個應力水平,頻率均為1 Hz,疲勞初始點的體積應變也不盡相同(從-0.15%~-0.42%),致使巖樣的疲勞振幅和最終破壞時的循環次數也各不相同,振幅從477~725 kN,次數從845~22 640次。
3.2 疲勞損傷演化規律分析
從圖7可知,巖石動態循環加卸載過程的應力-應變曲線呈3種不同形式,即“疏-密-疏”,由此可將巖石疲勞變形過程對應劃分為3個階段,也即初始增長階段、穩定增長階段和快速增長階段。同時,軸向應變和橫向應變的規律雖然都呈現3個階段,但其變形速率卻完全不同,橫向應變的增長速率?軸向應變,表明在巖石動態循環加卸載的疲勞過程中,巖石受側向膨脹的影響遠大于軸向壓縮影響,也即側向膨脹對巖石疲勞變形過程起主導作用。此外,從軸向應變曲線可知,巖石的彈性模量隨循環加載次數的增加呈逐漸減小的趨勢,且減小的速率也可分為快速減小、勻速減小、加速減小3個階段,這與曲線呈現的“疏-密-疏”的形態一一對應,說明在疲勞損傷過程中,巖樣剛度呈逐漸劣化的趨勢,且劣化的速率呈“快速-穩定-加速”3個不同的特征階段。
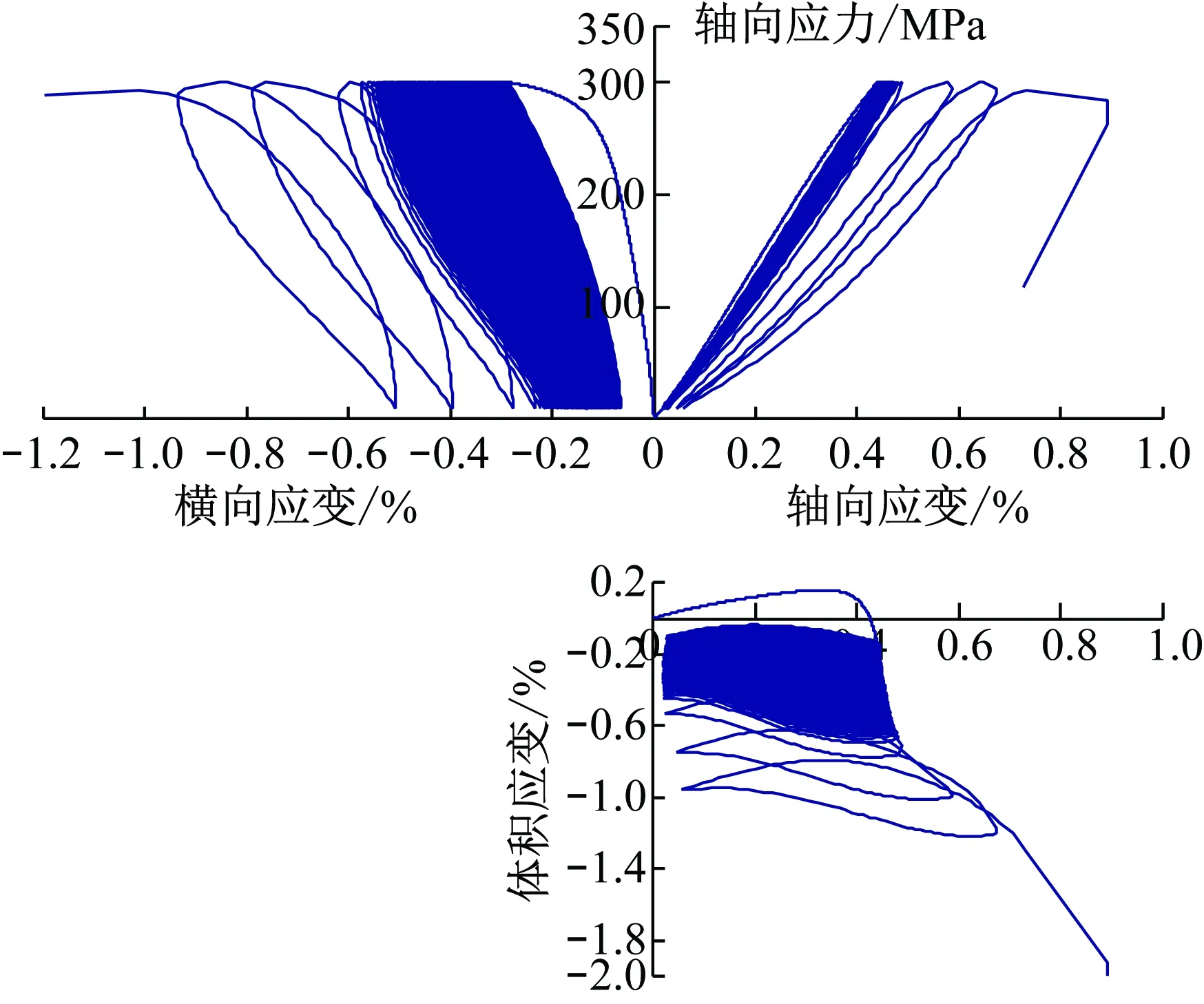
(a) 試樣BS18-1(5 MPa,1 Hz,-0.15%)

(b) 試樣BS18-2(12.5 MPa,1 Hz,-0.235%)
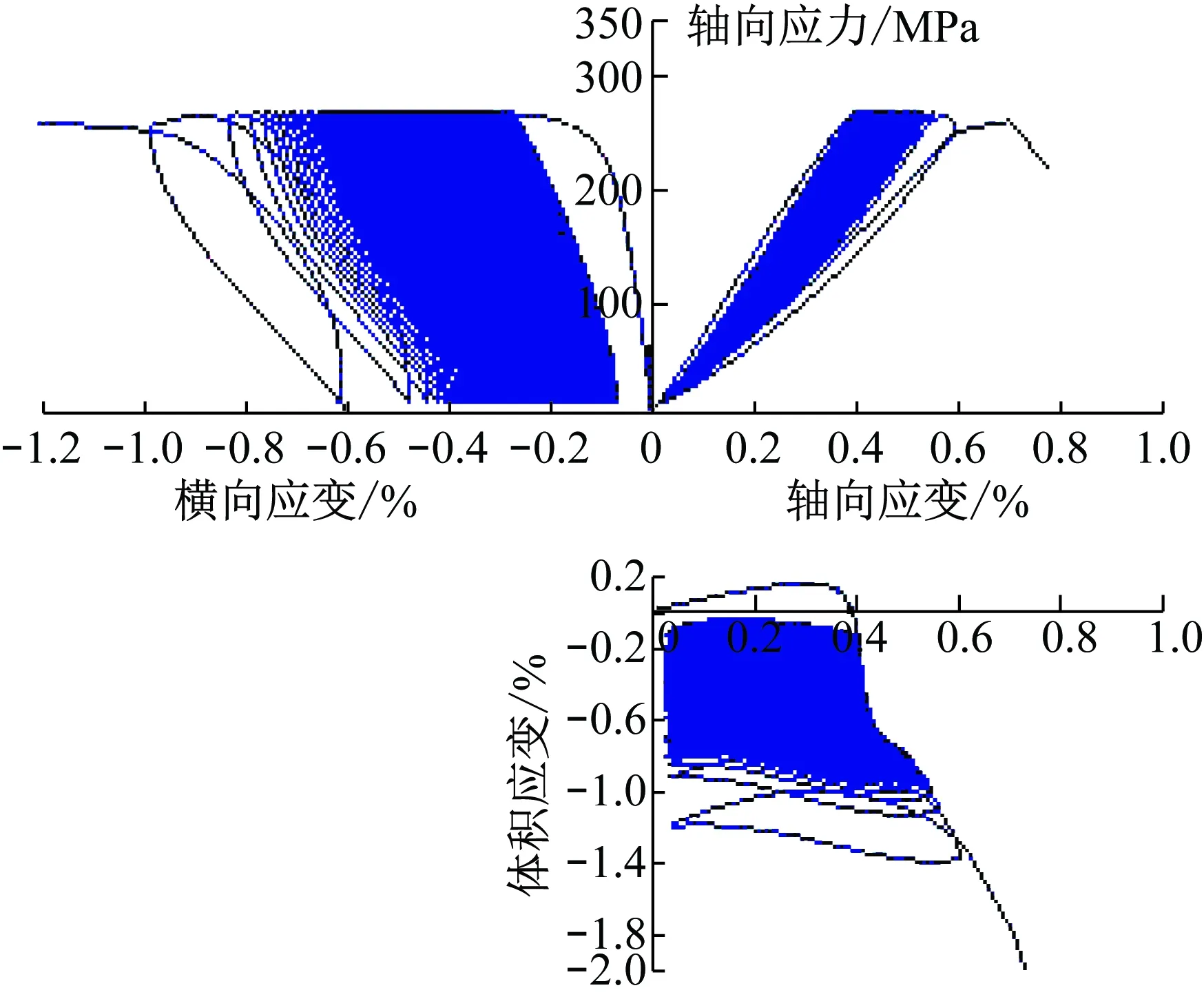
(c) 試樣BS18-3(2.5 MPa,1 Hz,-0.15%)
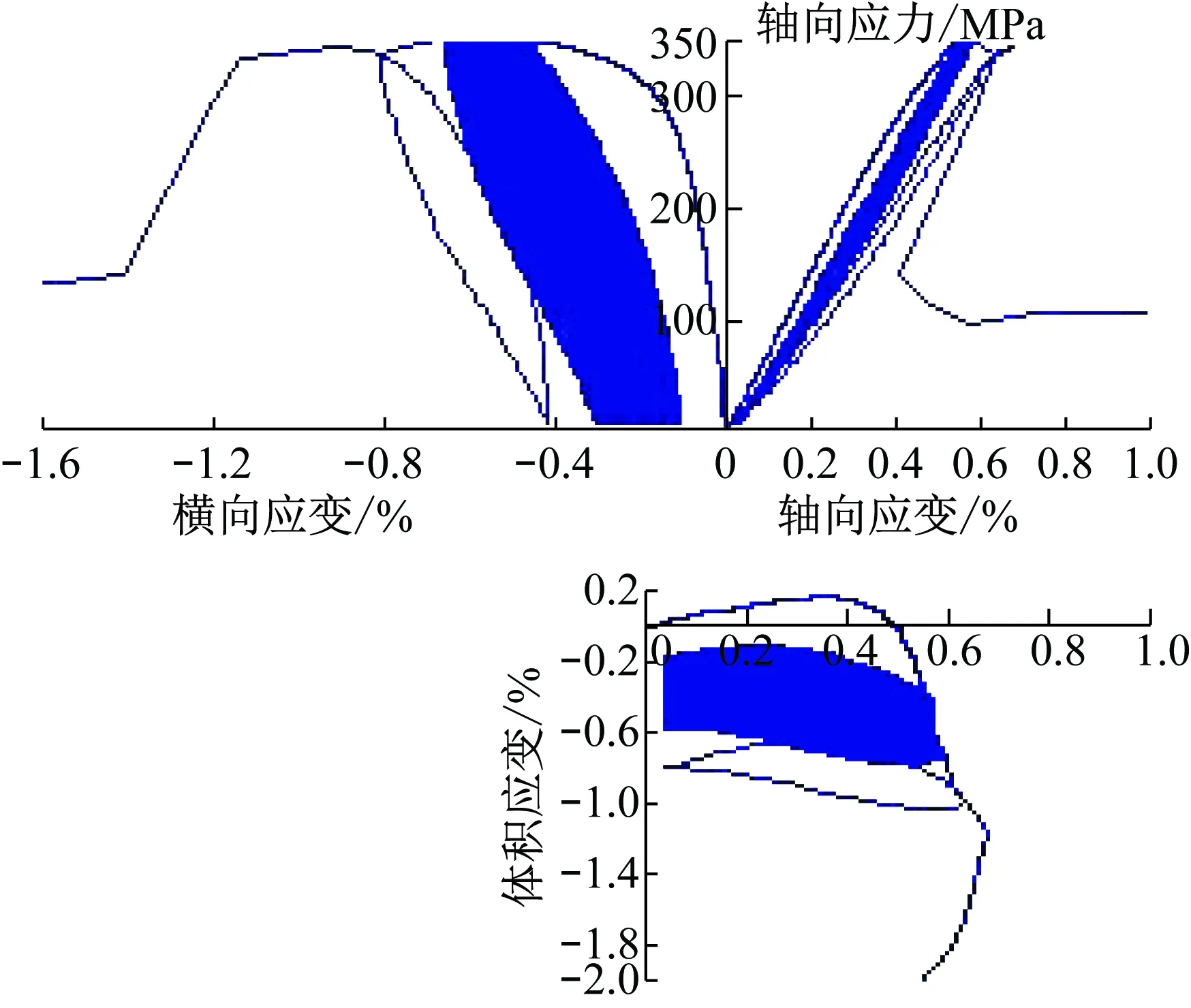
(d) 試樣BS18-5(10 MPa,1 Hz,-0.42%)
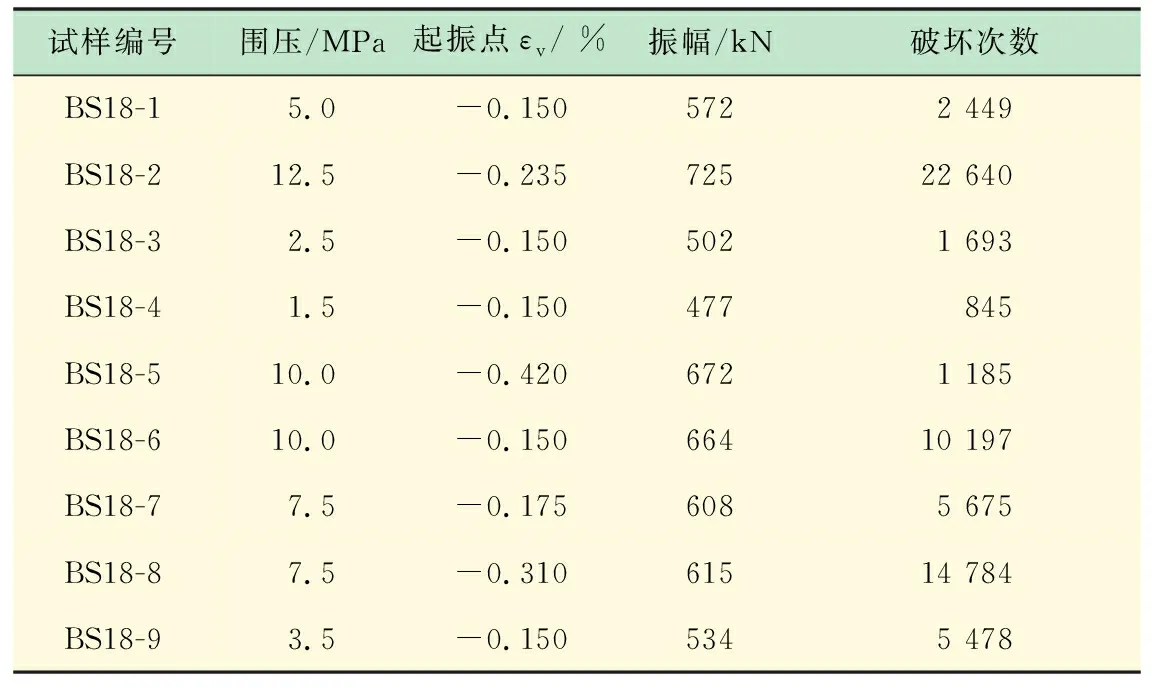
表1 不同圍壓下巖樣疲勞試驗結果
3.3 圍壓對疲勞損傷特性影響分析
巖石疲勞過程中每個加載段的彈性模量可按下式計算,另定義初始加載段彈模為ES,最后一次加載段彈模為Ef,
Ei=σi50%/εai50%
(1)
式中:σi50%為每個加載段50%峰值應力處應力值;εai50%為每個加載段50%峰值應力處處軸向應變值;i為動態加載次數。
表2為根據式(1)計算所得不同圍壓下巖樣疲勞過程中彈性模量和應變結果。圖8~10為不同圍壓對巖樣疲勞振幅、彈性模量和破壞瞬時應變的影響關系。從表1、表2和圖8~10可以看出,圍壓越大,巖樣的疲勞振幅越大,但其靜態加載階段的初始彈性模量呈輕微增大趨勢(64.88~71.65 GPa),最后一次循環加載階段的彈性模量無規律性變化,說明圍壓對巖樣的疲勞振幅影響顯著,但對其彈性模量無顯著影響。此外,巖樣疲勞破壞時的瞬時應變也呈現不同的規律變化,其軸向應變基本不隨圍壓變化而變化(基本在0.7%左右),而橫向應變變化明顯,呈現隨圍壓增大而減小的趨勢,說明圍壓越大,其側向膨脹越小,也進一步證實在巖石疲勞過程中,側向膨脹對其起主導作用。
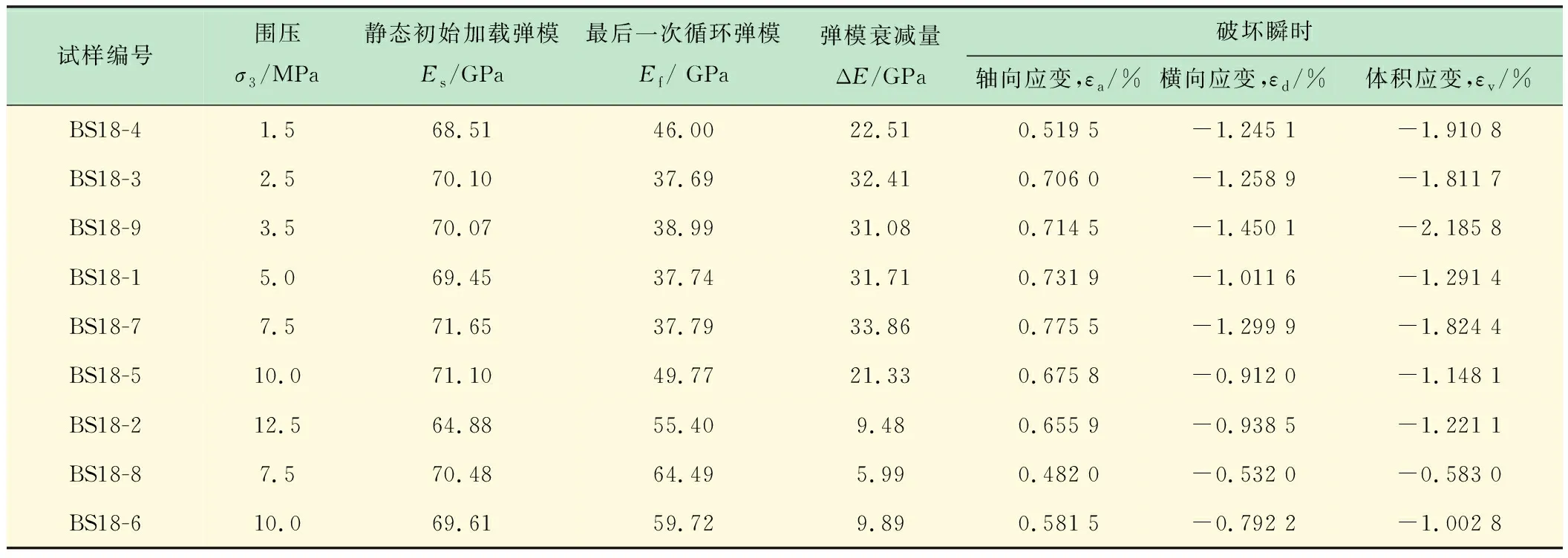
表2 不同圍壓下巖樣彈性模量與破壞時的瞬時應變結果
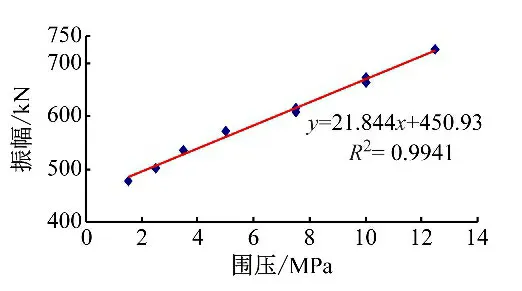
圖8 圍壓對巖樣疲勞振幅的影響
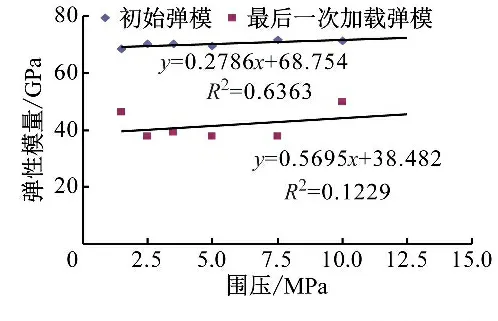
圖9 圍壓對巖樣彈性模量的影響
圖11為不同圍壓條件對巖石疲勞壽命的影響關系曲線,其中圖11(a)為振幅與疲勞起始點體積應變均隨圍壓變化;而圖11(b)的起始點體積應變固定,只有振幅隨圍壓變化而變化。從圖中可看出,若振幅與起始點損傷(即體積應變)均變化,巖石的疲勞壽命受圍壓影響不夠顯著;而當起始點損傷固定,只有振幅變化時,則巖石的疲勞壽命明顯依賴于圍壓條件且呈指數規律變化。
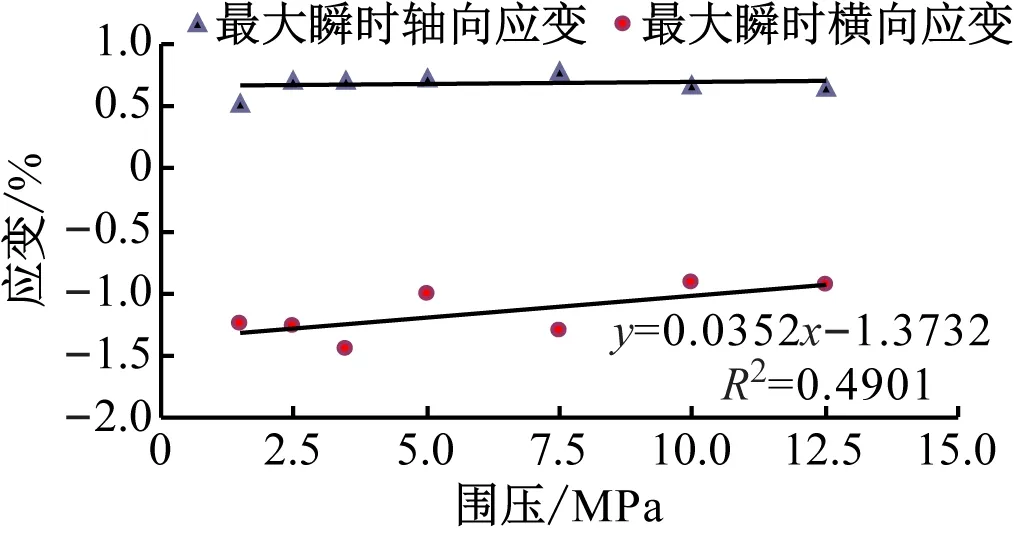
圖10 圍壓對巖樣破壞瞬時應變的影響
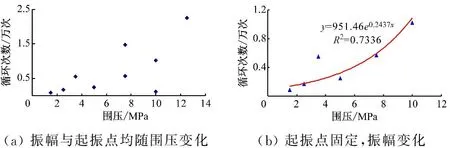
(a) 振幅與起振點均隨圍壓變化(b) 起振點固定,振幅變化
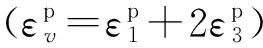
(2)
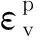
圖12為部分巖樣損傷變量與圍壓的關系曲線。由圖可知,圍壓對巖樣的損傷演化特征影響顯著,當巖樣的初始損傷值相同,巖樣破壞時所需的加、卸載循環次數隨圍壓增加而變多,即巖樣的疲勞壽命越長。然而,即使在高圍壓條件下,當巖樣的初始損傷超過一定值時,其疲勞壽命也會明顯縮短,如試樣BS18-5(圍壓10 MPa,次數1 185)。
圖12 不同圍壓下損傷變量Dvol隨循環次數的演化規律
4 結 語
通過本次試驗,以北山花崗巖為研究對象,針對其在不同圍壓、不同振幅、但固定頻率的條件下,研究了花崗巖在圍壓條件下的疲勞損傷演化規律,并分析了不同圍壓對疲勞損傷特性的影響,得出的主要結論如下:
(1) 圍壓條件下巖石疲勞損傷過程可分為初始、穩定、加速3個階段,其應力-應變曲線形態為“疏-密-疏”。巖石應變隨循環次數增加而逐漸增加,但橫向應變的變化速率?軸向應變,說明側向膨脹對巖樣的疲勞損傷演化過程起主導作用。
(2) 巖石的彈性模量隨循環加載次數的增加而逐漸減小,且同樣呈現“快速-勻速-加速”3個階段,反映了巖石的剛度隨疲勞損傷過程的發展而逐漸劣化的趨勢。
(3) 圍壓條件對巖石的疲勞振幅影響顯著,且隨圍壓增大而增加,但對彈性模量和破壞瞬時軸向應變無明顯影響,對橫向應變卻影響明顯,進一步反映了側向膨脹對疲勞損傷過程的主導作用。此外,巖石的疲勞壽命與圍壓和初始損傷息息相關,隨著圍壓的增加,巖樣在疲勞破壞時對應的最大塑性體積應變總體上表現出逐漸減小的趨勢。當巖樣的初始損傷值一定時,其疲勞破壞的循環次數隨著圍壓的增大而增加,即巖樣的疲勞壽命越長。

