基于帶符號滑動窗口的ECC抗功耗攻擊算法

王 超

(南陽理工學(xué)院 軟件學(xué)院，河南 南陽 473004)

0 引 言

橢圓曲線密碼(Ellipse Curve Cryptography, ECC)在安全性相同的情況下，由于與其他公鑰密碼算法相比具有密鑰長度短，處理速度快、存儲空間小等優(yōu)點(diǎn)，使得橢圓曲線密碼非常適用于系統(tǒng)級芯片(System on Chip, SoC)等資源受限但安全性需求高的各類系統(tǒng)中[1-2]。但是由Kocher[3]于1998年提出的功耗攻擊對基于ECC的SoC芯片帶來了極大安全威脅，功耗攻擊主要根據(jù)SoC芯片中密碼算法運(yùn)算泄露的功耗信息，通過統(tǒng)計(jì)分析出功耗和密鑰的相關(guān)性來獲取密鑰。在橢圓曲線密碼中實(shí)施抗功耗攻擊最關(guān)鍵的運(yùn)算是標(biāo)量乘運(yùn)算，然而采取抗功耗攻擊措施會降低運(yùn)算效率，但是可以通過對標(biāo)量采用不同的編碼方法來改進(jìn)運(yùn)算效率。其中，傳統(tǒng)的二進(jìn)制抗功耗攻擊算法是通過添加偽操作來掩蓋功耗差異，雖然該算法可以抵抗功耗攻擊，但會大幅降低標(biāo)量乘運(yùn)算效率。近年來，一些研究人員提出了各種改進(jìn)算法[4-6]。文獻(xiàn)[7]中提出通過將密鑰分解成長度相同的多組短密鑰，然后在最優(yōu)組合坐標(biāo)系下計(jì)算標(biāo)量乘算法，可以保證安全性的情況下有效提升運(yùn)算效率。文獻(xiàn)[8]中提出了一種基于帶符號雙基數(shù)系統(tǒng)的抗功耗攻擊方案，該方案主要是利用帶符號雙基數(shù)系統(tǒng)對標(biāo)量重新編碼，同時結(jié)合基點(diǎn)掩碼技術(shù)，以達(dá)到保證安全效率和提升運(yùn)算效率的雙重目標(biāo)。文獻(xiàn)[9]中提出了一種基于帶符號整數(shù)拆分形式的抗功耗攻擊方案，該方案通過將標(biāo)量進(jìn)行帶符號的整數(shù)拆分形式編碼，并采用基點(diǎn)掩碼和標(biāo)量分割方法實(shí)現(xiàn)抗功耗攻擊，同時運(yùn)算效率也有了一定提高。

為解決基于ECC的SoC芯片存在安全和效率之間的矛盾問題，給出了一種基于帶符號滑動窗口的ECC抗功耗攻擊算法(resisting power attacks algorithm based on Signed Sliding Window for elliptic curve cryptography，SSW)，所給算法主要是利用帶符號滑動窗口對ECC標(biāo)量乘法中的標(biāo)量進(jìn)行重新編碼，并利用預(yù)計(jì)算、基點(diǎn)掩碼和底層域2kR+S方法，實(shí)現(xiàn)了在抗功耗攻擊的同時提高標(biāo)量乘運(yùn)算的效率，可以很好地解決橢圓曲線密碼標(biāo)量乘算法存在安全與效率矛盾的問題，能夠較好地應(yīng)用在SoC芯片等各類資源受限的系統(tǒng)中。

1 帶符號滑動窗口標(biāo)量乘算法

標(biāo)量乘運(yùn)算是橢圓曲線密碼中的關(guān)鍵運(yùn)算，其計(jì)算式為：

(1)

式中:Q和P為橢圓曲線上的兩個點(diǎn);k為標(biāo)量。

經(jīng)典的標(biāo)量乘算法一般采用二進(jìn)制編碼的方式，將標(biāo)量乘運(yùn)算分解為點(diǎn)加運(yùn)算和倍點(diǎn)運(yùn)算。基于二進(jìn)制編碼形式的標(biāo)量乘運(yùn)算為：

(2)

式中:n為二進(jìn)制編碼長度，單位為bit;ki為二進(jìn)制編碼系數(shù)，且有ki∈{0,1}。下面給出橢圓曲線密碼基于二進(jìn)制編碼的標(biāo)量乘算法:

算法1二進(jìn)制編碼的標(biāo)量乘算法

輸入：k，P；

輸出：Q=kP。

(1) 令Q=O；//其中O無窮遠(yuǎn)點(diǎn)

(2) 對于變量i從n-1到0，則重復(fù)執(zhí)行：

Q=2Q；

如果ki=1，則有Q=Q+P；

(3) 返回Q。

帶符號的滑動窗口算法[10]主要是針對標(biāo)量k的二進(jìn)制編碼，用寬度為w+1的窗口對其進(jìn)行分組，如果窗口中的最高位是1時，則表示該窗口的值為負(fù)數(shù)，即此時窗口的值應(yīng)采用補(bǔ)碼表示(窗口中所有二進(jìn)制位取反，末位加1)，同時需要產(chǎn)生一個進(jìn)位。則標(biāo)量k的帶符號滑動窗口編碼系數(shù)是由{-2w+1,…,-3,-1,0,1,3,…,2w-1}中元素組成。文獻(xiàn)[11]中給出證明：采用帶符號滑動窗口編碼可將一個n比特二進(jìn)制序列轉(zhuǎn)化為具有最少非零個數(shù)的編碼形式，且其非零位平均個數(shù)是n/(w+2)。則有標(biāo)量k的帶符號滑動窗口編碼為：

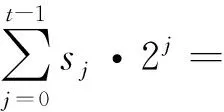
2(2…(2(2·st-1+st-2)+st-3)…+s1)+s0

(3)

式中:sj為標(biāo)量k的帶符號滑動窗口編碼;t為標(biāo)量k的帶符號滑動窗口編碼長度。其中j∈{0,1,…,t-1}，且有sj∈{-2w+1,…,-3,-1,0,1,3,…,2w+1}。下面給出標(biāo)量k的帶符號滑動窗口編碼算法:

輸入：正整數(shù)k；

輸出：(st-1,st-2,…,sj,…s1,s0)。

(1) 對于變量j從0到t-1，則重復(fù)執(zhí)行：

如果sj=0，則執(zhí)行j=j+1；

如果sj=1，則執(zhí)行：

如果sj+w=1，則執(zhí)行：

對于項(xiàng)目成本的控制，具體實(shí)施過程中不能只局限于紙上談兵，或是以犧牲施工質(zhì)量和安全為手段來達(dá)到降低項(xiàng)目成本的目的。在施工過程中，現(xiàn)場人員要進(jìn)行現(xiàn)場蹲守，多觀察，勤思考，多溝通，隨時進(jìn)行調(diào)整，達(dá)到創(chuàng)新的目的。應(yīng)該根據(jù)合同要求的工程項(xiàng)目、質(zhì)量、進(jìn)度等指標(biāo)，詳細(xì)地編制好施工組織設(shè)計(jì)，作為制定計(jì)劃成本的基礎(chǔ)。對合同中的暫定項(xiàng)目和存在變更的分項(xiàng)工程，要進(jìn)行嚴(yán)格審核，及時申報(bào)，避免返工、窩工以及浪費(fèi)。

kj+w+1=kj+w+1+1；

對于j從j+1到j(luò)+w+1，則有sj=0；

j=j+w+1；

(2) 返回(st-1,st-2,…,sj,…s1,s0)。

根據(jù)式(3)標(biāo)量k的帶符號滑動窗口編碼，則可得基于帶符號滑動窗口的標(biāo)量乘運(yùn)算為：

(4)

式中,Pj=sj·P需要通過預(yù)計(jì)算求出，也即構(gòu)造一個預(yù)計(jì)算表{(-2w+1)P,…,-3P,-P,3P,…,(2w-1)P}，可用于主運(yùn)算執(zhí)行時查詢調(diào)用。由此可知，基于帶符號滑動窗口的標(biāo)量乘算法主要分為3個步驟：一是標(biāo)量k的帶符號滑動窗口編碼；二是構(gòu)造預(yù)計(jì)算表Pj；三是執(zhí)行主循環(huán)運(yùn)算，求出Q=kP。下面給出基于帶符號滑動窗口標(biāo)量乘算法的具體描述:

算法3基于帶符號滑動窗口的標(biāo)量乘算法

輸入：k，P；

輸出：Q=kP。

(1) 計(jì)算(st-1,st-2,…,sj,…s1,s0)；

(2) 構(gòu)造預(yù)計(jì)算表Pj；

(3) 令Q=O；//其中O無窮遠(yuǎn)點(diǎn)

(4) 對于變量j從t-1到0，重復(fù)執(zhí)行：

Q=2Q；

如果sj>0，則有Q=Q+Pj；

(5) 返回Q。

式中，預(yù)計(jì)算表Pj的生成方法如算法4所示。

算法4預(yù)計(jì)算表Pj生成算法

輸入：w，P；

輸出：預(yù)計(jì)算表Pj。

(3) 對于j從1到2w-1-1，則執(zhí)行：

P2j+1=P2j-1+P2；

(4) 返回Pj。

2 功耗攻擊及其防御

功耗攻擊根據(jù)所采取的攻擊手段不同[12]，主要可以分為簡單功耗攻擊(Simple Power Attack, SPA)與差分功耗攻擊(Differential Power Attack, DPA)。其中，針對ECC的功耗攻擊主要有零值點(diǎn)功耗攻擊(Zero-value Power Attack, ZPA)與修正功耗攻擊(Refined Power Attack, RPA)。目前，抵抗功耗攻擊的防御措施主要有電路層級與算法層級兩類。電路層級的抗功耗攻擊措施[13]主要是功耗恒定和功耗互補(bǔ)技術(shù)，通過設(shè)計(jì)無功耗泄露的基本電路單元，或是增加一個互補(bǔ)的電路單元，來構(gòu)建高安全性的密碼模塊。算法層級的抗功耗攻擊措施包括添加偽操作、隨機(jī)化密鑰和基點(diǎn)掩碼等。其中，基點(diǎn)掩碼[14]是最為廣泛的抗功耗攻擊方法，其基本思想主要是通過引入一個或多個隨機(jī)數(shù)與密碼算法中生成的中間結(jié)果執(zhí)行一定的算術(shù)或邏輯運(yùn)算，以隨機(jī)化加密算法中的所有中間結(jié)果以及泄露相關(guān)的功耗能量信息，實(shí)現(xiàn)對SoC芯片內(nèi)部運(yùn)算數(shù)據(jù)的掩蓋，使得攻擊者無法從外部可探測功耗信息與內(nèi)部的中間運(yùn)算數(shù)據(jù)的相關(guān)性，以實(shí)現(xiàn)抵抗功耗攻擊的目標(biāo)。

簡單功耗攻擊是通過測量密碼算法的功耗信息來猜測在某時刻對應(yīng)的運(yùn)算過程及操作次數(shù)，以此判斷該時刻所對應(yīng)的密鑰信息。目前抵抗簡單功耗攻擊的措施主要包括添加偽操作、歸一化標(biāo)量乘法和統(tǒng)一的點(diǎn)加和倍點(diǎn)操作等。

差分功耗攻擊是通過測量密碼算法的多次功耗曲線，然后對其進(jìn)行統(tǒng)計(jì)分析來獲取密鑰，不需要考慮密碼算法的具體實(shí)現(xiàn)細(xì)節(jié)。目前抵抗差分功耗攻擊的措施主要包括隨機(jī)化密鑰、隨機(jī)化基點(diǎn)、隨機(jī)化曲線參數(shù)和隨機(jī)化投影坐標(biāo)等。

零值點(diǎn)功耗攻擊是通過測量寄存器為0時所獲得的有效功耗曲線，以此來區(qū)分標(biāo)量乘運(yùn)算中的點(diǎn)加和倍點(diǎn)運(yùn)算，進(jìn)而獲取密鑰信息。目前抵抗零值點(diǎn)功耗攻擊的措施主要包括基點(diǎn)掩碼和標(biāo)量分割等。

修正功耗攻擊是利用特殊點(diǎn)(x,0)或(0,y)使隨機(jī)化投影坐標(biāo)的方法無法起作用，進(jìn)而可以使攻擊者采用DPA攻擊以獲取密鑰。目前抵抗修正功耗攻擊的措施主要包括基點(diǎn)掩碼和標(biāo)量分割等。

3 基于SSW抗功耗攻擊算法

所給基于SSW抗功耗攻擊算法的基本思想是首先利用帶符號滑動窗口編碼算法對標(biāo)量進(jìn)行重新編碼，以使編碼形式的非零位個數(shù)最少；然后引入一個隨機(jī)點(diǎn)R，用以實(shí)現(xiàn)隨機(jī)盲化基點(diǎn)的目的，并將隨機(jī)點(diǎn)結(jié)合在預(yù)計(jì)算中生成新的預(yù)計(jì)算表；最后利用底層域直接計(jì)算2kR+S的方法[15]執(zhí)行標(biāo)量乘運(yùn)算，不僅可以歸一化點(diǎn)加和倍點(diǎn)操作，同時還可以提高運(yùn)算效率。下面給出基于SSW抗功耗攻擊算法的具體描述過程，主要可以分為如下3個步驟：

步驟1利用算法2求得標(biāo)量k的帶符號滑動窗口編碼形式，即:

sj∈{-2w+1,…,-3,-1,0,1,3,…,2w+1}

步驟2引入一個隨機(jī)點(diǎn)R，令P1=P-R，然后利用算法4求得基點(diǎn)隨機(jī)盲化后的預(yù)計(jì)算表Tj。

步驟3采用底層域直接計(jì)算2kR+S的方法來執(zhí)行標(biāo)量乘法運(yùn)算，一方面不僅可以提升運(yùn)算效率，另一方面也可以歸一化點(diǎn)加和倍點(diǎn)操作，使得執(zhí)行標(biāo)量乘法運(yùn)算時沒有功耗差異。同時值得注意的是，在主運(yùn)算中令Q=R，用以抵消在預(yù)計(jì)算中加入隨機(jī)點(diǎn)的影響，恢復(fù)出真實(shí)的返回值。

下面給出基于帶符號滑動窗口抗功耗攻擊算法的具體描述，如算法5所示。

算法5基于帶符號滑動窗口抗功耗攻擊算法

輸入：k，P；

輸出：Q=kP。

(1) 計(jì)算(st-1,st-2,…,sj,…s1,s0)；

(2) 隨機(jī)點(diǎn)R=random()；

(3) 構(gòu)造預(yù)計(jì)算表Tj；

(4) 令Q=R；

(5) 對于變量j從t-1到0，重復(fù)執(zhí)行：

如果sj>0，則有Q=2jQ+Tj；

(6) 返回Q。

其中，預(yù)計(jì)算表Tj生成算法的具體描述，如算法6所示。

算法6預(yù)計(jì)算表Tj生成算法

輸入：w，P；

輸出：預(yù)計(jì)算表Tj。

(1) 隨機(jī)點(diǎn)R=random()；

(4) 對于j從1到2w-1-1，則執(zhí)行：

T2j+1=T2j-1+T2；

(5) 返回Tj。

4 算法性能分析

4.1 安全性分析

在所給算法5的步驟5中，由于采用了底層域直接計(jì)算2kR+S，使得在主循環(huán)運(yùn)算中歸一化了點(diǎn)加操作和倍點(diǎn)操作，其功耗曲線不會出現(xiàn)明顯差異，因此所給基于SSW抗功耗攻擊算法可以抵抗簡單功耗攻擊SPA。

在所給算法5的步驟4中，由于令Q=R，使得在執(zhí)行主循環(huán)運(yùn)算時掩蓋了中間運(yùn)算結(jié)果和功耗之間的差異，使得攻擊者無法對所獲取的功耗曲線進(jìn)行統(tǒng)計(jì)分析，因此所給基于SSW抗功耗攻擊算法可以抵抗差分功耗攻擊DPA。

在所給算法5的步驟3中，預(yù)計(jì)算Tj時引入了一個隨機(jī)點(diǎn)R，實(shí)現(xiàn)了對原始基點(diǎn)進(jìn)行了盲化，使得在執(zhí)行步驟5的主循環(huán)運(yùn)算中無法找到特殊點(diǎn)(x,0)或(0,y)，同時也無法測量寄存器為0時的功耗曲線，攻擊者無法利用特殊點(diǎn)或零值寄存器來獲取有用的功耗曲線，因此所給基于SSW抗功耗攻擊算法可以抵抗零值點(diǎn)功耗攻擊ZPA和修正功耗攻擊RPA。

4.2 運(yùn)算效率分析

算法5的步驟1中，計(jì)算標(biāo)量k帶符號滑動窗口編碼的運(yùn)算量與標(biāo)量乘的運(yùn)算量相比可以忽略不計(jì)。算法5的步驟3中，構(gòu)造預(yù)計(jì)算表Tj需要執(zhí)行一次倍點(diǎn)運(yùn)算和2w-1次點(diǎn)加運(yùn)算，則構(gòu)造預(yù)計(jì)算表Tj所需的運(yùn)算量為DA+2w-1·AA(下標(biāo)A表示是在仿射坐標(biāo)下計(jì)算)。算法5的步驟5中，主循環(huán)運(yùn)算需要執(zhí)行n/(w+2)次底層域直接計(jì)算2kR+S，則主循環(huán)運(yùn)算所需的運(yùn)算量為n/(w+2)·DDAJA(下標(biāo)JA是在雅克比坐標(biāo)系+仿射坐標(biāo)系下計(jì)算)。其中，A表示點(diǎn)加運(yùn)算，D表示倍點(diǎn)運(yùn)算，DDA表示底層域直接計(jì)算2kR+S。表1給出了算法5與二進(jìn)制抗功耗攻擊算法和基于密鑰分解抗功耗算法的運(yùn)算量比較。

表1 算法5與其他經(jīng)典抗功耗攻擊算法的運(yùn)算量比較

通常認(rèn)為橢圓曲線密碼中512bit的密鑰是安全的，即n=512。令采用的窗口寬度為4，則有w=3。其中，d表示密鑰分段的個數(shù)，且取d=4。在仿射坐標(biāo)系下，AA的計(jì)算量為S+2M+I，DA的計(jì)算量為2S+2M+I；在雅克比坐標(biāo)系下，AJ的計(jì)算量為4S+12M，DJ的計(jì)算量為6S+4M；在仿射坐標(biāo)系+雅克比坐標(biāo)系下，AJA的計(jì)算量為3S+8M，DDAJA的計(jì)算量為(4w+3)S+(4w+9)M[16]，tJ→A的計(jì)算量為44M。其中，M表示模乘運(yùn)算，S表示平方運(yùn)算，I表示模擬運(yùn)算，且有I=20M和S≈M。表2給出了算法5與二進(jìn)制抗功耗攻擊算法和基于密鑰分解抗功耗算法的運(yùn)算效率比較。

表2 算法5與其他經(jīng)典抗功耗攻擊算法的運(yùn)算效率比較

從表2可以看出，所給算法5的總運(yùn)算效率比二進(jìn)制抗功耗攻擊算法提升了71.47%，比基于密鑰分解的抗功耗攻擊算法提升了45.46%。同時可以看出，所給算法5所需的預(yù)計(jì)算運(yùn)算效率比基于密鑰分解抗功耗攻擊算法的預(yù)計(jì)算運(yùn)算效率提升了97.29%，這表明所給算法5在SoC芯片中占用的存儲資源也較少。所以對于SoC芯片等資源受限的各類應(yīng)用系統(tǒng)，所給算法5更加便捷高效。綜上可知，所給基于帶符號滑動窗口抗功耗攻擊算法不僅可以抵抗SPA、DPA、RPA和ZPA等多種功耗攻擊，而且運(yùn)算效率也得到大幅提升，同時占用存儲空間也較小。因此，所給算法5能夠同時兼顧安全和效率兩方面，可以較好地應(yīng)用在各類資源受限的系統(tǒng)中。

5 結(jié) 語

功耗攻擊由于其實(shí)現(xiàn)簡單和成功率高等優(yōu)點(diǎn)，使得橢圓曲線密碼在抵抗功耗攻擊的過程中面臨著安全和效率矛盾的問題。標(biāo)量乘法是橢圓曲線密碼中的關(guān)鍵運(yùn)算，通過進(jìn)一步對標(biāo)量進(jìn)行帶符號滑動窗口編碼，大大減少了編碼中的非零位個數(shù)，同時結(jié)合預(yù)計(jì)算、基點(diǎn)掩碼和底層域直接計(jì)算，從而實(shí)現(xiàn)抵抗功耗攻擊的目的。與二進(jìn)制抗功耗攻擊算法和基于密鑰分解的抗功耗算法相比，所給基于帶符號滑動窗口抗功耗攻擊算法可以在確保相同的安全性情況下，進(jìn)一步提升橢圓曲線密碼標(biāo)量乘法運(yùn)算的效率，可以較好地應(yīng)用在各類資源受限的系統(tǒng)中，具有較好的理論研究和實(shí)際應(yīng)用價值。