不同條件下兩種方法計算雨水設計流量的比較
肖君健
(武漢市規劃設計有限公司,湖北 武漢 430014)
0 引言
雨水設計流量是確定城市雨水管渠規模的重要指標,其計算方法及取值的合理性直接關系到工程的經濟性和安全性。在城市雨水管網設計時,通常采用推理公式法來計算最大設計流量。隨著計算機技術的發展和產匯流理論的逐漸完善,數學模型如 SW M M 、Di gi t al W at er、Inf oW orks CS、M IKE URBAN等被應用于計算雨水管網的設計流量。2016年版《室外排水設計規范》(以下簡稱新版規范)中,補充規定了推理公式法的適用范圍:“當匯水面積超過2 km2時,宜考慮降雨在時空分布的不均勻性和管網匯流過程,采用數學模型法計算雨水設計流量。”根據新版規范,城市雨水管渠雨水設計流量的計算存在推理公式法和數學模型法兩種并列方法[1-2],并指出當匯水區面積較大時,推理公式法具有一定的局限性。推理公式法的計算結果相對數學模型法是偏大或是偏小,除了受匯水區面積大小影響外,兩種方法計算結果是否還受匯水區水文形狀、地面集水時間t1取值等因素的影響,還有待研究。因此有必要開展數學模型法和推理公式法在不同匯水區面積、匯水區形狀系數等條件下的比較分析,以期為城市雨水管渠設計流量的計算方法選擇及其合理取值提供參考。
1 數學模型的選取
隨著新版規范的發布及全國城市排水防澇規劃編制的開展,數學模型如EPASW M M、Di gi t al W at er、Inf oW orks CS、DH I M IKE 等被廣泛應用于模擬城市暴雨徑流過程。其中,EPA SW M M模型是由美國環境保護署推出的基于水文水動力學的一維分布式城市暴雨徑流管理數學模型,可用于模擬降雨地表產流、地表匯流、管網水動力學傳輸過程,其產匯流理論和計算引擎被Di gi t al W at er、M IKE SW M M、XP SW M M、PC SW M M 等模擬軟件廣泛借鑒。在廣州、武漢、黃岡等地已開展的城市水系規劃及排水規劃中對EPA SW M M、Inf oW orks CS、DH I M IKE 進行了應用[3-4],相對于 EPA SW M M這一開源軟件,后期的商業模擬軟件增加了數據預處理、結果分析、動態展示等功能。本文從模型的產匯流原理出發,選取EPA SW M M作為數學模型研究工具。
2 兩種方法的理論基礎
2.1 推理公式法
2.1.1 公式形式
目前廣泛應用于城市雨水管渠設計流量的推理公式,英、美稱為“合理化公式”,蘇聯稱為“穩定情勢公式”,由愛爾蘭人摩爾凡尼于1851年提出[5]。原始形式見式(1):

式中:Q為雨水設計流量,L/s;q為暴雨強度,L/(s·hm2);ψ為徑流系數;F為匯水面積,hm2。
推理公式法需結合暴雨強度公式使用,我國常用的暴雨強度公式形式見式(2):
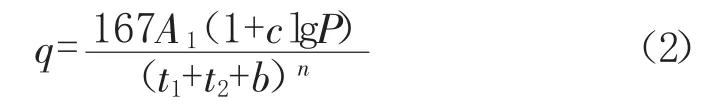
式中:A1、c、b、n 為地方參數,根據統計方法計算確定;t1為地面集水時間,m i n;t2為管內雨水流行時間,m i n;P為設計重現期,年。
2.1.2 公式基本假定
(1)降雨在整個匯水面積上的分布是均勻的。
(2)降雨強度在選定的降雨時段內均勻不變。
(3)匯水面積隨集流時間增長的速度為常數。
2.2 數學模型法
該方法包括地表產流計算模型、地表匯流計算模型和管網匯流計算模型。
2.2.1 地表產流計算模型
將城市下墊面概化為三種不同分區,包括透水區域、有滯蓄量的不透水區域、無滯蓄量的不透水區域。對于有滯蓄量的不透水區域,產流量為降雨量減去洼地的填充量。對于透水區域,產流量為降雨量減去透水區域的滯蓄量和下滲量之和。對于透水區域的下滲計算,SW M M模型中有霍頓(H ort on)下滲模型、格林安普特(Green-Am pt)下滲模型和CN(Curve Num ber)模型可供選擇。本文采用霍頓下滲模型,該模型假定下滲率在最初降雨時為最大值,隨著降雨的持續,下滲率逐漸減小,最后達到穩定,此時的下滲率為穩定下滲率。城市雨水管渠集水區域面積較小,集水時間短,采用短歷時設計暴雨,降雨過程中的蒸發量小,故產流計算時不考慮蒸發損失。
2.2.2 地表匯流計算模型
SW M M模型中,將子匯水區的三個不同分區近似概化為矩形的非線性水庫,采用非線性水庫法計算每個子匯水區出流量。
2.2.3 管網匯流計算
SW M M模型提供了兩種求解非恒定流方法,包括運動波法、動力波法。運動波法假定水面坡度等于導管坡度,運用連續的動量方程求解,不能模擬回水、逆流、有壓流的情況;動力波法是通過求解完整圣維南方程組來進行匯流演算。
2.3 輸入與輸出對比
相對于推理公式法,數學模型法在產匯流理論基礎上進行細化,兩者輸入的參數和輸出的結果不同。將輸入參數分為確定性參數和經驗性參數,確定性參數可根據現狀資料得到,經驗性參數需根據長期實測降雨流量資料率定后確定或參考同類地區確定。兩種方法輸入與輸出對比見表1。

表1 兩種方法輸入與輸出對比分析表
3 對比方案設計
3.1 變量選擇
新版規范在建議采用數學模型法時是以匯水面積為主要指標,由表1可以看出,推理公式法和數學模型法在參數輸入與結果輸出時存在不同,綜合考慮后確定以下設計變量:
(1)匯水面積。新版規范中提出,“當匯水面積超過2 km2時,宜考慮降雨在時空分布的不均勻性和管網匯流過程,采用數學模型法計算雨水設計流量”,已表明匯水面積是設計流量計算方法選擇時的重要參考因素。因此將匯水區面積作為對比方案的自變量進行分析。
(2)匯水區形狀系數。為匯水區平均寬度與匯水區長度之比,而匯水區平均寬度為匯水區面積與匯水區長度之比。匯水區形狀系數可表示為f=F/L2(F為匯水區面積,L為匯水區長度)。扇形匯水區的形狀系數較大,狹長形匯水區的形狀系數則較小。中國各地區包括湖北、廣東等省編制《暴雨徑流查算圖表》時,將匯水區形狀系數作為匯流參數取值的依據。城市雨水管網一般呈樹枝狀形態,匯水區面積一定時,匯水區形狀的不同將會影響支管峰值徑流到達干管的時間,從而影響峰值徑流遭遇過程,最終影響排水干管峰值流量。因此將匯水區形狀系數作為對比方案的自變量進行分析。
(3)因變量。徑流量峰值。
3.2 基本假定
3.2.1 匯水區模型
將匯水區概化為若干子匯水區,子匯水區均設為面積0.1 km2(400 m×250 m)的矩形區域,子匯水區的不透水率設為60%,子匯水區的平均坡度為0.5%。雨水干管(橫向)長度設為400 m,雨水干管(縱向)長度設為250 m,雨水管坡度設為0.3%。為比較推理公式法和數學模型法在不同匯水區形狀系數下的計算結果,子匯水區的排列概化為以下三種基本形式,如圖1~圖3所示。

圖1 排列形式一
圖2 排列形式二
圖3 排列形式三
不同排列形式的匯水區形狀系數f計算:

3.2.2 設計暴雨
采用武漢暴雨強度公式計算兩年一遇設計暴雨總量,芝加哥過程線模擬暴雨過程,雨峰系數取為0.4。
3.2.3 管道平接方式
不同的管道平接方式會導致水力坡度不同,對徑流峰值流量會有一定影響。管頂平接的水力坡度大于管底平接,按照一般性設計原則,采用管頂平接方式搭建管道模型。搭建管道數學模型時,雨水管徑需要通過試算確定,以保證排水處于臨近滿流狀態,而不出現溢流。雨水管道糙率取為0.013。
3.2.4 出流狀態
采用自由出流設計,即下游排水口無頂托。
3.3 模型參數校準
由表1可以看出,數學模型法中需要確定的經驗性參數較多,經驗性參數需要長期的實測降雨及流量資料進行參數率定,而我國大部分城市已建排區尚未建立完善的排水防澇監測系統,新建排區在規劃設計之初也無實測數據。模型參數若不進行校準,隨意定量,模擬結果將不具備可靠性。因此在參考SW M M模型手冊和同類文獻[3-4]基礎上,確定數學模型參數的初始值,再基于綜合徑流系數對數學模型中的經驗性參數進行校準,以保證模型參數的可靠性。
4 結果分析
4.1 兩種方法對匯水面積的響應分析
匯水區模型采用排列形式一(見圖1),其中匯水區個數n為30,即總的匯水區面積為3.0 km2。采用SW M M數學模型法模擬排區的暴雨徑流過程,即可得到不同匯水區面積(0.1~3.0 km2)的峰值流量。同時采用推理公式法計算不同匯水區面積的峰值流量,集水時間t1取10 m i n。兩種方法對匯水面積的響應分析見表2。
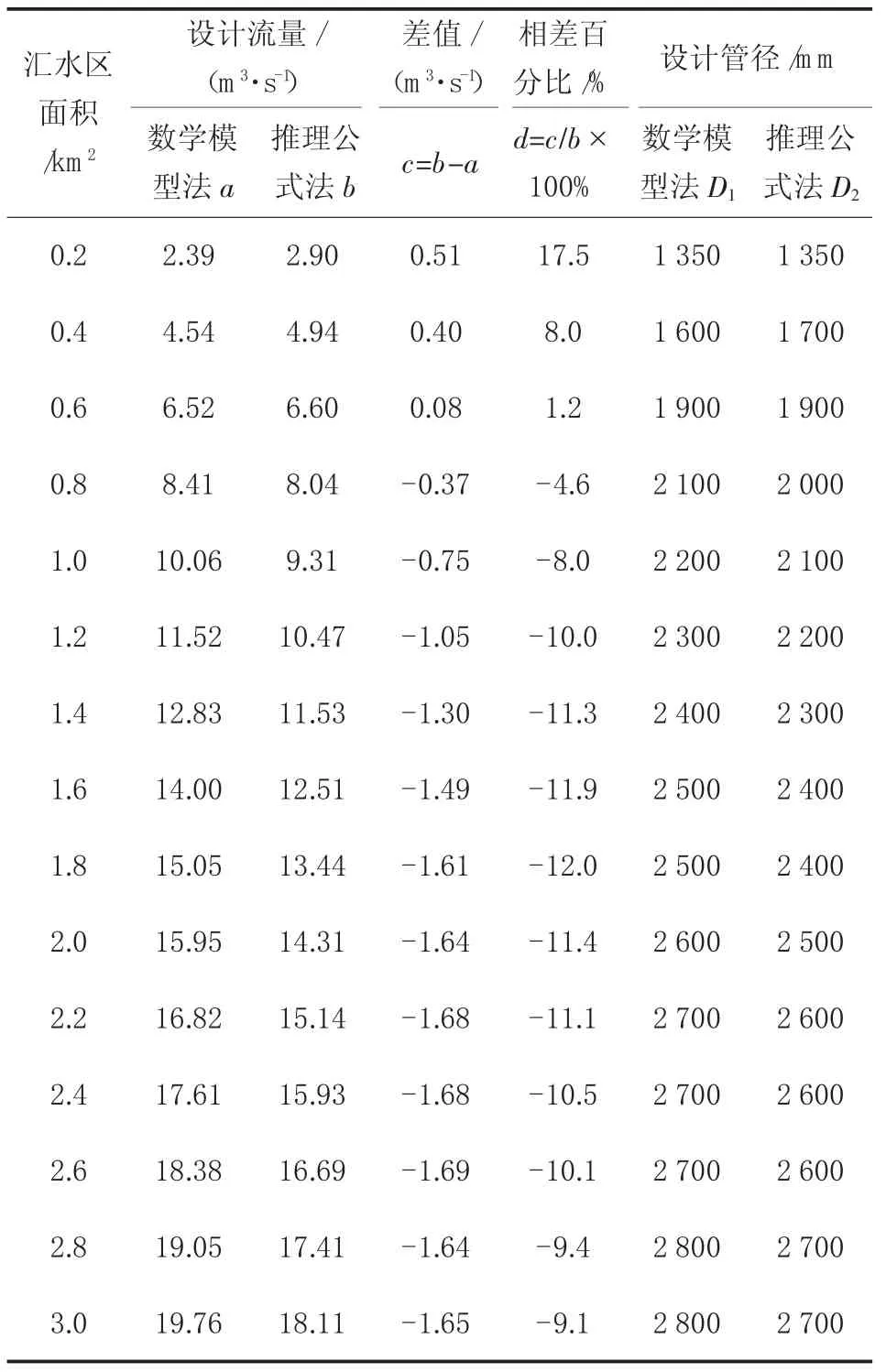
表2 兩種方法對匯水面積的響應分析對比
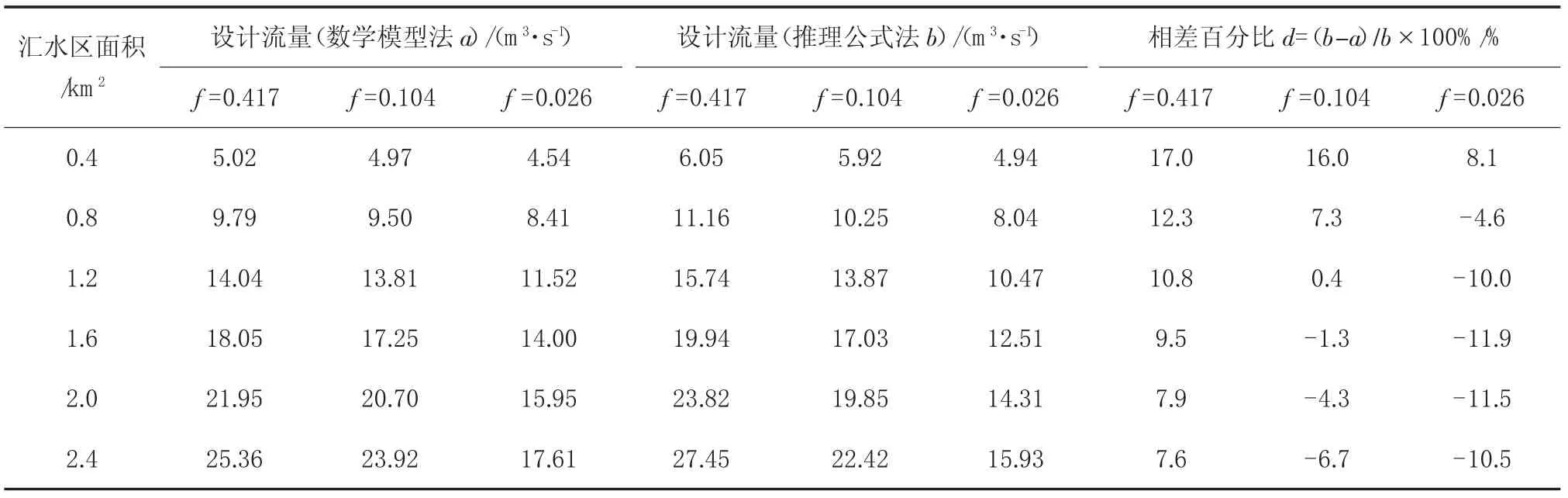
表3 兩種方法對匯水區形狀系數的響應分析對比
由表2可知:
(1)當匯水區面積小于0.6 km2時,數學模型法計算的設計流量小于推理公式法,隨著匯水區面積的增大,相差百分比逐漸縮小;當匯水區面積為0.6 km2時,兩者結果相當;當匯水區面積大于0.6 km2時,隨著匯水區面積的增大,相差百分比先增大后縮小,且不大于12%。
(2)兩種方法的設計管徑隨著設計流量增大而增大,且兩種方法在同一匯水區面積時的設計管徑相差不超過100 m m。
4.2 兩種方法對匯水區形狀系數的響應分析
匯水區模型分別采用圖1~圖3的三種排列形式,其中匯水區個數n為24,即總的匯水區面積為2.4 km2。經計算,三種排列形式的匯水區形狀系數 f分別為 0.417、0.104、0.026。
采用SW M M數學模型法模擬匯水區的暴雨徑流過程,即可得到同一面積下不同形狀系數時的峰值流量。同時采用推理公式法計算同一面積下不同形狀系數時的峰值流量,集水時間t1取10 m i n。兩種方法對匯水區形狀系數的響應分析見表3。
由表3可知:
(1)同一匯水面積時,設計流量與匯水區形狀系數f相關,f值越大,即匯水區形狀越偏于扁平,設計流量越大。
(2)不同匯水面積時,匯水區形狀系數越大,推理公式法計算結果偏于安全;匯水區形狀系數越小,數學模型法偏于安全。
5 結語
通過對匯水區下墊面和管網進行概化,研究了數學模型法和推理公式法的輸入參數與輸出結果的不同,在以綜合徑流系數校準數學模型基本參數的基礎上,比較了兩種方法在不同的匯水面積、匯水區形狀系數等不同設計條件下的雨水流量計算結果,可以得出以下結論:
(1)對于匯水區面積小于3 km2或雨水管徑小于d3 000 m m的雨水管網設計,兩種方法計算結果相當,采用推理公式法簡易且較為可靠;匯水區形狀系數越大,推理公式法計算結果偏于安全。
(2)對于匯水區面積大于3 km2的城市排水干渠,匯水面積較大,匯流時間長,以短歷時暴雨強度公式為基礎的推理公式法不宜使用,往往采用1~3 d長歷時設計暴雨,建議參考水利部門所采用的排澇計算方法[3-4],根據匯水區內是否有存在較大蓄水容積、有無客水流經、自排或是抽排等情況,確定排水設施的適宜規模。

