無限大帶電體產生的電場及其零電勢點的選取
陳龍法
(石獅市第一中學 福建 泉州 362700)
無限大的帶電體實際上并不存在,它只是一種模型.然而,這是一個有事實基礎的模型.對于均勻帶電的有限長的棒和有限大的板,在其附近的地方,只要不太靠近端點或邊緣,滿足適當條件后,就可被視為無限長帶電棒和無限大的帶電板.在電磁學中,常見的有無限長帶電直線、無限長帶電圓柱或圓筒、無限大帶電平面等.這類帶電體因電荷分布不在有限區域,不宜簡單地規定無窮遠處電勢為零,而應根據具體問題中的電場強度空間分布特點,靈活選取合適的零電勢點.
1 無限大(長)均勻帶電體的電場強度
1.1 無限長均勻帶電直線所產生的電場強度
【例1】如圖1所示,一無限長均勻帶電直線,電荷的線密度為λ(設λ為正).離帶電直線為r處的任一點P的場強大小為
寫成矢量形式為

圖1 例1題圖
1.2 無限長均勻帶電圓柱面所產生的電場強度
【例2】一無限長均勻帶電圓柱面,半徑為R,電荷面密度為σ.求其產生的場強分布.
設場點P到軸線的距離為r.
當r>R時,即場點P在圓柱面外,如圖2所示,根據高斯定理,有
由此得出

圖2 點P在圓柱面外的示意圖
如果令λ=2πRσ為圓柱面上單位長度的電荷量,則上式可化為
可見無限長均勻帶電圓柱面外的場強,與將所帶電荷全部集中在軸線上的均勻帶電直線所產生的場強一樣.
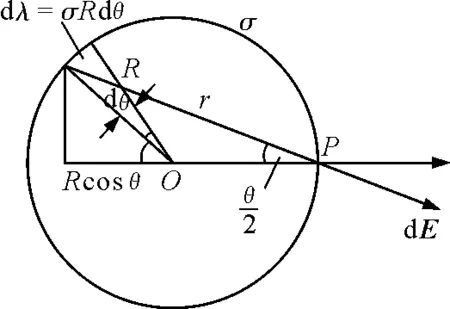
當r 為了求出無限長均勻帶電圓柱面所在處的場強,可將這個圓柱面看成是無數多個帶電直線構成,計算這些直線電荷在圓柱面上某一點P產生的電場強度.這個圓柱面的橫截面是一個圓,如圖3所示.圖中θ角度處的線電荷dλ=σRdθ在P點產生的場強為 圖3 圓柱面的橫截面示意圖 dE在圓柱面法線方向上的分量為 積分后得到 因此,無限長均勻帶電圓柱面產生的場強分布,寫成矢量式為 無限長均勻帶電圓柱面產生的場強分布,用圖像表示,則如圖4所示. 圖4 無限長均勻帶電圓柱面產生的場強分布圖 【例3】設有一無限大均勻帶電平面,電荷面密度為σ,求場強分布. 如圖5所示,根據電場分布的對稱性特點,取柱體表面為高斯面,其軸線與帶電平面垂直,兩底與帶電面平行,并對帶電平面對稱.設底面面積都等于S,根據高斯定理,有 即 圖5 取柱體表面為高斯面 上式表明,無限大均勻帶電平面的場強E的大小與場點到帶電平面的距離x無關. 寫成矢量形式為 在無限大均勻帶電平面的面電荷所在處,有 在帶電平面的另一面,面電荷所在處,有 【例4】兩個相同的無限大均勻帶電平行平面,相距為d,帶等量異號電荷,電荷的面密度分別為σ和-σ.求其場強分布. 根據前面的分析和電場強度疊加原理,如果以兩面中間為原點,沿單位矢量n的方向取x軸,n為從σ到-σ的法線方向,則兩個相同的無限大均勻帶電平行平面產生的電場,在各處的場強分布如下: 作出的E-x圖像,如圖6所示. 圖6 兩個帶等量異號電荷的無限大均勻帶電平行平面產生的場強 點電荷的庫侖定律是一個可靠的以實驗為基礎的定律,是靜電場的一切概念和規律的出發點.點電荷q在距離為r處產生的電場強度為 電荷所產生的靜電場是保守場,因此,可以用電勢來描述靜電場,即對于靜電場中的每一點,都可以定義一個電勢φ.靜電場中A,B兩點的電勢差通常定義為:單位正電荷從A移到B靜電場力做的功,即 在點電荷q的電場中,A和B兩點的電勢差為 因而 φr-φ 或 式中φr,φ分別是離點電荷q為r和無窮遠處的電勢. 正如物體的高度、溫度等必須有參考點(零點)一樣,靜電場中某一點的電勢也必須有一個參考點(零點).在靜電場中,通常規定無窮遠處的電勢為零,即規定φ=0. 在這個規定下,靜電場中任一點P的電勢為 點電荷q在距離為r處產生的電勢為 可見,電場中某一點的電勢等于該點與零電勢點的電勢差,而且這個零電勢點是人為主觀規定的,并非由自然規律得出的客觀結論.處理某個問題時必須采用同一個零電勢點,但在不同的問題里可以選用不同的零電勢點.例如,在靜電學里,通常規定無窮遠處的電勢為零,而在電路的問題里,常規定地球的電勢為零. 無限大帶電體的電勢問題,關鍵是如何規定零電勢點的問題. 當電荷分布在有限區域時,可以規定離這些電荷為無窮遠處的電勢為零.這樣做最方便,也不會引起任何矛盾.但當帶電體為無限大時,這樣做就會出問題了. 【例5】如圖7所示,設有一個無限大的均勻帶電平面,電荷的面密度為σ.若選取無窮遠處的電勢為零,求距離帶電平面為r處的電勢. 圖7 例5題圖 在距離帶電平面為r處,電場強度為 距離帶電平面為rA和rB的兩點之間的電勢差為 這表明在有限范圍內,任意兩點的電勢差都具有確定的值. 圖8 點P電勢分析圖 這里是不是積分路徑移動方向出現問題所帶來的錯誤呢?上面講的A趨于無窮遠是相對于P點的,但相對于電荷來說并不是趨于無窮遠,而是仍在有限的距離內. 因而只要規定無窮遠處電勢為零,無論沿著什么路徑方向積分,都會出現問題. 【例6】設電荷均勻分布在兩個無限大的平行平面上,面電荷密度分別為σ和-σ,相距為d,如圖9所示.若選取無窮遠處的電勢為零,求在離帶電平面為r處的電勢. 圖9 例6題圖 由此可得這兩個面電荷所在處的電勢差為 那么,在無限大帶電體的電場中,如何解決零電勢點的選取問題呢? 當電荷分布在有限區域,規定離電荷無窮遠處的電勢為零對于解決問題很方便.但在處理與無限大帶電體的電勢有關問題時,就不宜選擇無窮遠處的電勢為零.由于零電勢點是人為規定的,因而可以根據具體情況,按照使計算盡可能簡單的原則來選擇電勢零點. 一個無限大(長)的帶電體,常見的有以下幾種: (1)一個無限大的均勻帶電平面 對于一個無限大的均勻帶電平面,電荷的面密度為σ.可以規定平面上(即電荷所在處)的電勢為零,這時,離帶電平面為r處的電勢為 (2)一條無限長的均勻帶電直線 對于一條無限長的均勻帶電直線,電荷線密度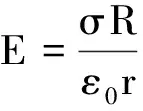

1.3 無限大均勻帶電平面所產生的電場強度


1.4 兩個帶等量異號電荷的無限大平行平面所產生的電場強度

2 電勢差及零電勢點
2.1 電勢差與電勢

2.2 零電勢點

3 帶電體為無限大時 選取無窮遠處為零電勢點所帶來的問題
3.1 帶電體為一個無限大的均勻帶電平面



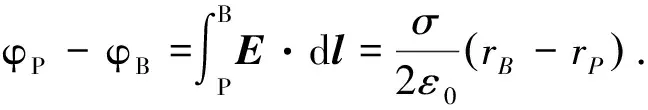
3.2 帶電體為相距一定距離的兩個無限大均勻帶電平面

4 帶電體為無限大時應該根據具體問題選取零電勢點
4.1 一個無限大(長)的帶電體其零電勢點的選取問題

