軌跡圓與磁場圓等大時帶電粒子運動模型分析
陳璽君
(丹陽市呂叔湘中學 江蘇 鎮江 212300; 廣西師范大學物理科學與技術學院 廣西 桂林 541004)
1 引言
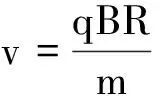
2 問題場景
在磁場教學中教師經常讓學生解決這樣一個問題:
【典例】如圖1(a)所示,x軸正方向水平向右,y軸正方向豎直向上.在xOy平面內有與y軸平行的勻強電場,在半徑為R的圓形區域內加有與xOy平面垂直的勻強磁場.在坐標原點O處放置一帶電微粒發射裝置,它可以連續不斷地發射具有相同質量m,電荷量q(q>0)和初速度為v0的帶電粒子.已知重力加速度大小為g.
(1)當帶電微粒發射裝置連續不斷地沿y軸正方向發射這種帶電微粒時,這些帶電微粒將沿圓形磁場區域的水平直徑方向離開磁場,并繼續沿x軸正方向運動.求電場強度和磁感應強度的大小和方向.
(2)調節坐標原點O處的帶電微粒發射裝置,使其在xOy平面內不斷地以相同速率v0沿不同方向將這種帶電微粒射入第Ⅰ象限,如圖1(b)所示.現要求這些帶電微粒最終都能平行于x軸正方向運動,則在保證勻強電場、勻強磁場的強度及方向不變的條件下,應如何改變勻強磁場的分布區域?并求出符合條件的磁場區域的最小面積.
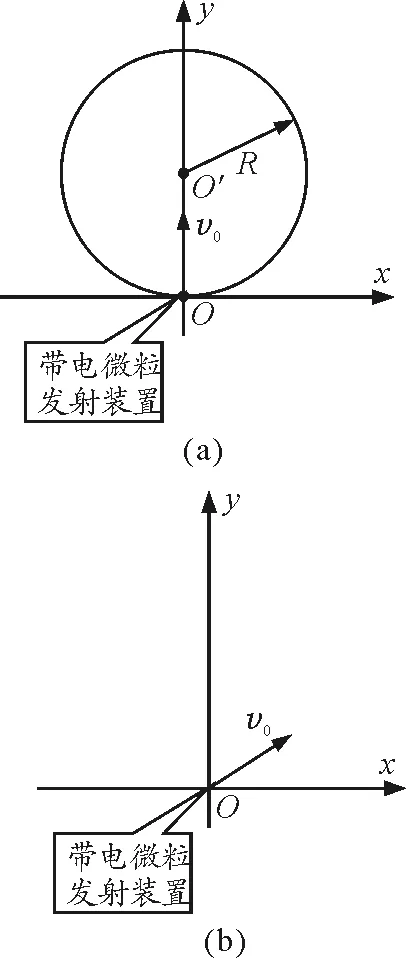
圖1 題圖
筆者發現,在教學過程中,對于典例中第(2)問的求解過程,學生感覺難度很大,如果在解決該問題之前,能夠先熟悉掌握以下運動模型,可以使教學變得從容,從而讓學生求解以上問題變得更加輕松.
3 模型概述
設圓形磁場方向垂直紙面向外,磁感應強度大小為B,一帶正電的微粒從圓形磁場圓形邊界A點入射.為方便討論,本文中帶電粒子的速率v不做特別說明均認為
其中q為帶電粒子的電荷量,B為圓形勻強磁場的磁感應強度,R為帶電粒子在勻強磁場中的圓軌跡半徑,亦為磁場圓的半徑,m為帶電粒子的質量,粒子的重力不計.
4 模型結論
結論1:帶電粒子以速率v從圓形勻強磁場邊界任意位置沿半徑射入磁場,必沿半徑方向射出磁場.
證明:如圖2所示,AO=BO=AO′=BO′,且AO⊥AO′,BO′⊥BO,故四邊形AOBO′為正方形,BO⊥BO′,因此vB與BO在一條直線上,沿半徑方向射出磁場.
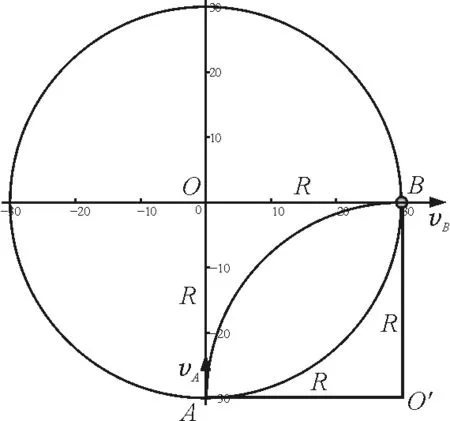
圖2 結論1分析圖
結論2:帶電粒子以速率v從圓形勻強磁場邊界任意位置以任意方向進入磁場,則粒子出磁場時的速度方向必垂直于粒子進磁場位置所在的圓直徑且平行于入射點磁場圓的切線.
證明:如圖3所示,過A點作直線AC與磁場圓相切,過B點作vB的反向延長線BD,O和O′為磁場圓與軌跡圓的圓心,AO=BO=BO′=AO′=R,故四邊形AOBO′為菱形,BD⊥AO,vB⊥AO,即vB⊥AE(直徑),而AC⊥AO,vB∥AC.
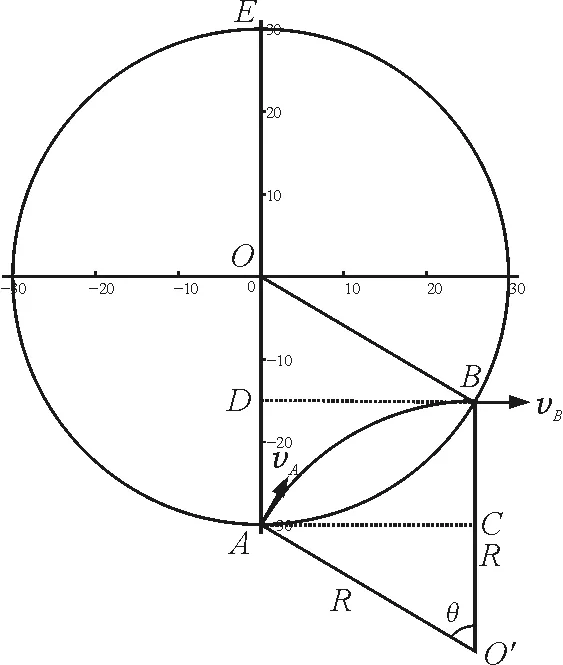
圖3 結論2情形1分析圖
證明:如圖4所示,過B點作vB的反向延長線BC,O和O′為磁場圓與軌跡圓的圓心,AO=BO=BO′=AO′=R,四邊形AOBO′為菱形,BO′∥AO,即BO′∥AD,而vB⊥BO′,故vB⊥AD(直徑),另AE⊥AD(直徑),vB∥AE.
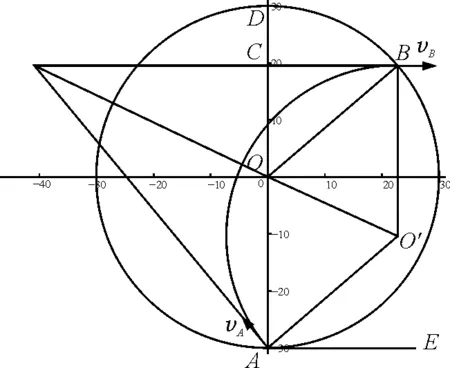
圖4 結論2情形2分析圖
結論3:大量相同的帶電粒子以速率v從圓形勻強磁場邊界任意位置以任意方向進入磁場,則所有帶電粒子離開磁場時速度方向必相同(平行).
證明:如圖5所示,由結論2的證明可知,從相同點入射的速率相同方向不同的帶電粒子出射方向均與同一直徑垂直或與入射點的同一切線平行,故帶電粒子出磁場的出射速度方向必互相平行.
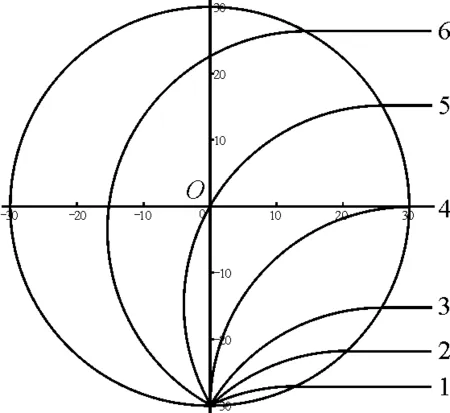
圖5 結論3分析圖
結論4:帶電粒子以速率v從圓形勻強磁場邊界任意位置以任意方向進入磁場,離開磁場時的速度方向與進入磁場時位置的垂直高度距離y最大值不超過2R,且滿足下列關系.
y=R(1-cosθ)
或
y=R[1+cos (π-θ)]
或
證明:以入射點A作為坐標原點,A點磁場圓切線為x軸,直徑為y軸,建立平面直角坐標系,設入射速度vA與x軸的夾角為θ.
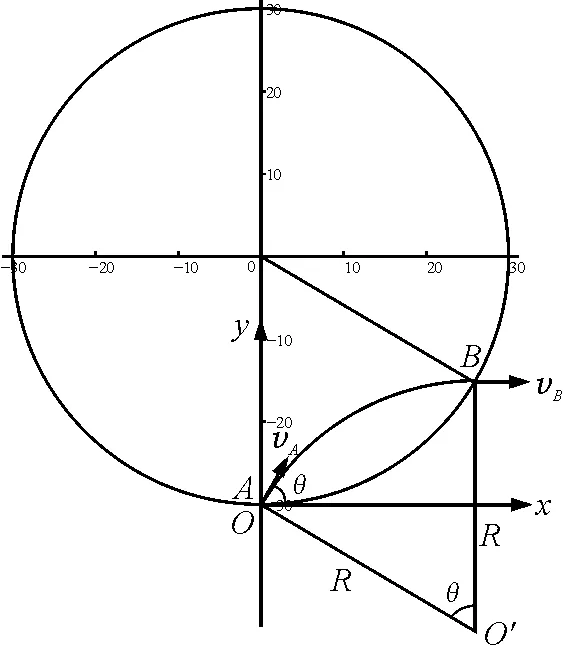
圖6 結論4當時的分析圖

圖7 結論4當時的分析圖
從圖7易知:就算入射角θ=π,即假如粒子能沿著磁場邊界做圓周運動,則y=2R,因此,帶電粒子離開磁場時的速度方向與進入磁場時位置的垂直高度距離y最大值不超過2R.
結論5:從圓形勻強磁場邊界任意位置以任意方向速度v進入磁場的帶電粒子1運動軌跡與以該粒子出磁場時的速度v反方向且速度等大進入圓形勻強磁場區域中帶電粒子2軌跡之和為定值s1+s2=πR,且帶電粒子1的入射點和帶電粒子2的出射點分別在磁場圓直徑的兩端點.
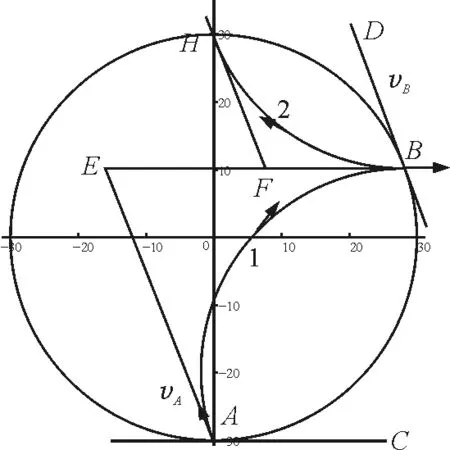
圖8 結論5證明分析圖
仿真實驗檢驗如圖9,圖10,圖11所示.
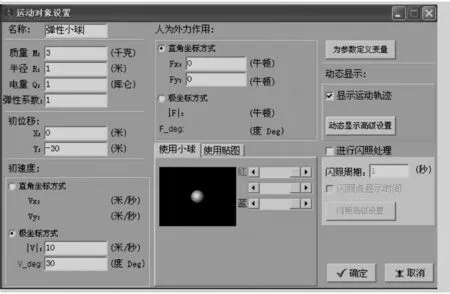
圖9 運動對象設置
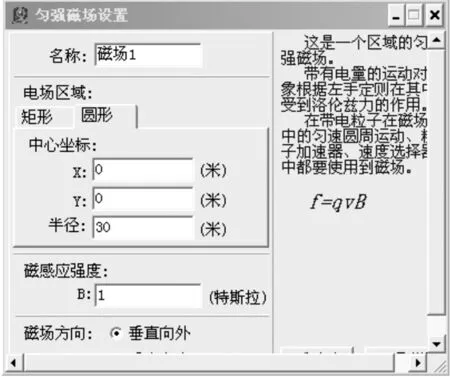
圖10 勻強磁場設置
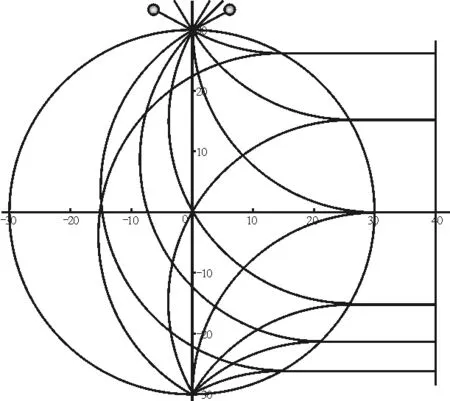
圖11 模擬結果
取磁場磁感應強度大小B=1 T,磁場半徑R=30 m,帶電小球質量M=3 kg,Q=1 C,彈性系數為1,在磁場右邊設置一塊豎直的彈性擋板,分別讓多個相同屬性的帶電小球(不設重力場)以相同大小的速率v=10 m/s,從A點以不同的入射角θ同時進入磁場,實驗發現所有的小球經過與入射點所在的直徑平行的彈性擋板反彈之后在直徑的另一端同時相遇,與理論預期一致.
5 問題解答
有了以上模型分析得出的結論,下面來解決文中一開始出現的典例.
5.1 分析
第(1)問由題目中“帶電粒子從坐標原點O處沿y軸正方向進入磁場后,最終沿圓形磁場區域的水平直徑離開磁場并繼續沿x軸正方向運動”可知:
其一,帶電微粒所受重力必與電場力平衡,洛倫茲力作向心力使得帶電微粒做勻速圓周運動.
其二,帶電微粒在磁場中做勻速圓周運動的軌跡圓半徑與磁場圓半徑必相等.
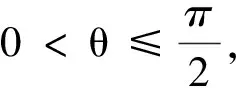
5.2 詳細解答
解:(1)由題目中“帶電粒子從坐標原點O處沿y軸正方向進入磁場后,最終沿圓形磁場區域的水平直徑離開磁場并繼續沿x軸正方向運動”可知,帶電微粒所受重力與電場力平衡.設電場強度大小為E,由平衡條件得
mg=qE
故
電場方向沿y軸正方向,帶電微粒進入磁場后,做勻速圓周運動,且圓運動半徑r=R.設勻強磁場的磁感應強度大小為B.由牛頓第二定律得
故
磁場方向垂直于紙面向外.
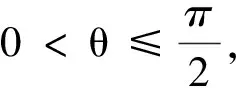
這樣磁場邊界上P點的坐標P(x,y)應滿足方程:
x=Rsinθy=R(1-cosθ)
所以磁場邊界的方程為
x2+(y-R)2=R2
(x-R)2+y2=R2
即為所求磁場的另一側的邊,因此,符合題目要求的最小磁場的范圍應是圓x2+(y-R)2=R2與圓(x-R)2+y2=R2的交集部分(圖12中陰影部分).由幾何關系,可以求得符合條件的磁場的最小面積為
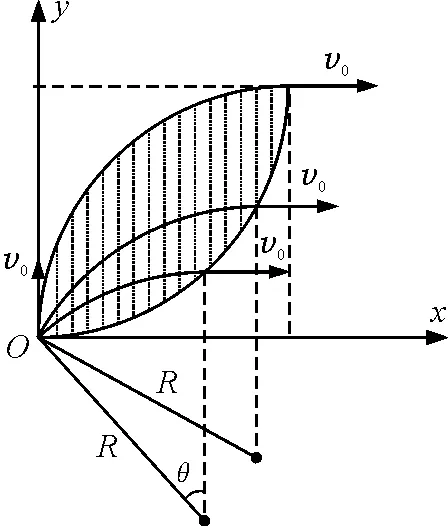
圖12 最小磁場范圍

