基于Keystone變換的弱目標積累檢測及工程實現方法

帥曉飛 朱玉軍 詹 旭

(1.中國兵器裝備集團成都火控技術中心 成都 611731; 2.四川理工學院自動化與電子信息學院 四川自貢 643000; 3.西南科技大學信息工程學院 四川綿陽 621000)

0 引言

當雷達檢測微弱目標時，常常需要目標積累時間遠大于常規處理，然而運動目標在長的積累時間內可能跨越多個雷達距離分辨單元，會大大減弱積累后目標信噪比。通過Keystone變換[1-7]校正PD雷達的距離走動，然后進行相參積累，達到提高信噪比的目標。

但是Keystone變換使原來的矩形信號采樣點變成了楔石(Keystone)形格式，需要對該楔石形格式的樣本點插值成為矩形格式才能采用FFT進行后續的相干積累。這個插值過程就是Keystone變換的實現過程，若直接用插值方法從楔石形格式的數據得到所需的矩形格式數據，雖然只是一維變換，但運算量巨大。為了工程實際應用，必須探索運算量較少的實現方法。而主要常用的工程實際應用的Keystone變換實現方法：DFT+IFFT算法、Chirp-Z變換法、sinc函數內插法和三階Lagrange內插法[1-7]。

本文在詳細分析Keystone變換校正PD雷達回波中目標距離走動的原理基礎上，介紹了四種常用的具體實現方法：DFT+IFFT的快速算法、Chirp-Z變換、sinc內插和三階Lagrange插值；通過詳細的理論推導證明了DFT+IFFT算法和Chirp-Z變換法的具體實現過程是相同的，并給出了上述三種不同實現方法具體運算量以及各算法的特點；最后，通過計算機仿真結果驗證了這四種算法的性能。

1 PD雷達回波模型與Keystone變換原理

設PD雷達載波中心頻率為fc，發射信號為：s(t)=p(t)exp(j2πfct)，其中p(t)表示基帶信號。

考慮速度為v的勻速運動目標，其雷達回波信號下變頻后：

(1)

對式(1)沿快時間維作傅里葉變換得：

(2)

(3)

將式(3)所示的Keystone變換代入式(2)，得到：

(4)

至此，距離走動得到了有效補償。

2 Keystone變換實現方法

對于式(3)所表示的Keystone變換中的距離頻率及慢時間都是以連續變量表示的，而在實際數字信號處理中是需要離散化處理的。為了便于工程實現，國內外許多學者給出四種實現算法[1-4]，本文經過仔細地推導比較發現其中兩種實現算法是相同的，只是推導的物理過程不同而已。

2.1 DFT+IFFT算法[2]

由(2)式到(4)式變換中，主要涉及到五個變量及其離散采樣，分別是快時間t(k)、快時間(距離)頻率f(l)和慢時間τm(m)、虛擬慢時間τn(n)及虛擬慢時間頻率fτ(n′)。并設快時間和快時間頻率的采樣點數目都為L，慢時間和虛擬慢時間及其頻率的采樣點數都為N。為了完成Keystone變換，對離散化的式(2)作二次離散傅里葉變換，具體地可以表示成

(5)

式(5)中，U′(l,n)并不一定精確等于式(4)所示的U(f,τ)的采樣值，因此用另一個符號表示。在上述步驟中，第一次DFT由于是變尺度的只能采用DFT，因為需要對所有距離頻率逐個計算M點DFT，其運算量比較大。為此，通過代換可用一種快速算法代替這個DFT運算。式(5)中括號內的式子又可以表示為：

(6)

上式后面求和部分可作如下變換：

(7)

經過式(6)和(7)的換算，式(5)表示的Keystone變換實現方法就可避開DFT而以FFT和點乘代替，大大提高運算效率。

2.2 Chirp-Z變換算法[1,3]

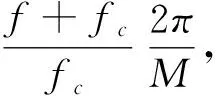
(8)

計算時沿z平面上的一段螺線做等分角的抽樣，記為：

zk=AW-k，k=0,1,…,M-1

(9)

上式中，M為所要分析的復頻譜的點數；A=A0exp(jθ0)，A0,θ0分別表示起始抽樣點的矢量半徑長度和相角；W=W0exp(jφ0)，W0,φ0表示螺線的伸展率和兩相鄰抽樣點之間的角度差。當M=N,A=1,W=exp(-j2π/N)時，式(9)就是DFT了。

(10)

事實上，式(10)正是式(5)中DFT部分，因此，Chirp-Z變換與DFT+IFFT變換兩種Keystone實現方法是完全相同的，即這兩種方法等效，本文將這兩種實現方法都稱為變尺度變換法。

2.3 sinc函數內插法[4]

另一種常用的Keystone變換實現方法為內插法，即每一個變換后的U′(l,n)值借助鄰近幾個慢時間離散取值點U(l,m)插值得到。內插方法很多，本文選用兩種較常用、效果也較好的：sinc內插法和三階Lagrange插值法。

插值就是待插值的樣本與內插核函數加權求和的一個過程。sinc內插法的公式可以表示為：

(11)

2.4 三階Lagrange內插法[5]

(12)

(13)

Lagrange插值方法具有整潔的結構，在理論研究和分析中很方便。事實上，常用的線性插值、二次插值都屬于Lagrange插值。然而，高階的Lagrange插值運算量很大，也存在嚴重的Runge現象，不利于實際運用。所以本文考慮三階Lagrange插值即取待插值處周圍的四個點對該處的值近似。

具體到公式(4)，令

ym=U(l,m)，xm=tm=mTr，I=4則可得對應的插值公式。對于n=0,1,…,M-1，找出滿足τm≤tn≤τm+1的序號m，并記τm-1,τm,τm+1,τm+2分別對應公式(12)中的x0,x1,x2,x3，此時，U′(l,n)可以表示為

U′(l,n)=U(l,m-1)l0(τn)+U(l,m)l1(τn)

+U(l,m+1)l2(τn)+U(l,m+2)l3(τn)

(14)

(15)

(16)

(17)

(18)

由以上推導結果不難得出，當樣本個數較少時，由于邊沿效應，插值后再相參積累的效果不理想。因此，三階Lagrange插值不適合樣本數較少的情況。

2.5 計算量分析[5]

設距離頻率域采樣點數為L，一個CPI內的脈沖數為M，M′為大于等于2M-1且為2的整數冪的最小正整數，通常為了后續相參積累的方便，M為2的整數冪，因此M′=2M。則對于以上三種Keystone變換實現方法：Chirp-Z變換、sinc內插法、三階Lagrange插值法在每一個距離頻率點上的運算量分別如下：

1)Chirp-Z變換：(2M+M′)點復數乘+3次M′點FFT+M點FFT。

2)sinc內插：M2點復數乘。

3)三階Lagrange插值法：20M點實數乘+4M點復數乘。

由上述分析可見，當M較大時，Chirp-Z變換和三階Lagrange在實際工程中實現起來比較容易些，而sinc內插法運算量稍大，實現起來相對困難些。

3 仿真結果

仿真參數：雷達發射線性調頻信號，信號帶寬為10MHz，時寬為10μs，雷達載頻為10GHz脈沖重復頻率為1kHz，目標徑向速度為1000m/s，回波脈壓前信噪比為-10dB，目標初始距離1.2km，CPI積累脈沖個數為256個。未進行Keystone變換時一個CPI內回波在脈沖間跨越了17個距離分辨單元。其數據對應的MTD積累結果如圖2所示，目標能量就分散在了相鄰多個距離單元內。

將圖1所示的數據分別進行第2節所述的三種Keystone變換實現方法得到的仿真結果分別如圖2、3、4所示：

圖2、圖3和圖4的結果表明，sinc內插、Lagrange插值和chirp-Z變換都能有效實現Keystone變換，能校正目標回波間的距離走動使MTD積累結果獲得更高的信噪比，有利于弱目標的檢測。

特別需要說明的是，在這一小節的仿真過程中，積累脈沖個數是256，可是當積累脈沖個數低于32，比如16時，Keystone變換后積累增益并不明顯，獲得的性能增益有限。

4 結束語

本文主要針對脈沖多普勒體制雷達中高速目標造成目標在回波中距離走動而使目標的相參積累效果嚴重下降的現象，研究了一種有效的校正距離走動的Keystone變換，主要對Keystone變換的實現方法進行了詳細討論，給出了每種實現方法的理論推導、具體實現步驟及計算量。仿真結果進一步驗證了每種實現方法的有效性。

鑒于Chirp-Z變換實現方法可以利用FFT實現，而FFT在DSP開發軟件中有標準、高效的庫函數，因此，Chirp-Z變換方法實現Keystone變換最易于工程實現。