積分在求和中的應用
(丹東市中醫藥學校 遼寧丹東 118000)
一、問題研究的背景
數學是一門應用性極強的學科, 積分學及其應用作為高等數學的一個分支, 在現實應用中的意義就更為顯著。它不僅是一門重要的數學分支, 而且在物理學, 生物學, 經濟學等領域及各種工程學科中有著極其重要的應用。
微積分是世界近代數學的重要內容, 也是近代數學進一步發展和拓展的重要基礎。微積分思想的萌芽出現得比較早, 中國戰國時代的《 莊子? 天下》 篇中的" 一尺之棰, 日取其半, 萬事不竭" , 就蘊涵了無窮小的思想。古希臘數學家阿基米德在公元前三世紀運用杠桿原理推導出了球體的體積公式, 就包含了定積分的基本原理。之后, 帕斯卡在求曲邊圖形的面積時, 用到了“無窮小矩形”的思想并把無窮小概念引入數學, 為后來萊布尼茨的微積分的產生奠定了基礎。
積分求和是伴隨著微積分學一起發展起來的學科。 1686年, 萊布尼茨又發表了他的第一篇積分學論文《深奧的幾何與不可分量及無限的分析》, 初步論述積分或求積問題與微分或切線問題的互逆關系。在這篇論文中, 積分號第一次出現在出版物上。積分求和有著深刻而生動的實際背景, 它從生產實踐與科學技術中產生, 又成為現代科學技術中分析問題與解決問題的一個強有力的工具。積分求和成為了有自己的目標和方法的新的數學分支。
近年來, 國內外學者對積分求和做了許多研究, 無論是在深度還是廣度方面都取得了重大發展。 積分求和在理論和實踐過程中起著非常重要的作用。
二、本文的主要工作
第一部分給出積分的一些相關性質, 這些性質將為我們對積分在求和問題中的研究奠定基礎。
第二部分利用積分的一般理論來找尋積分在求和應用中的例子。
第三部分利用積分性質, 逐步延深到積分在求和中的應用。
三、預備知識
首先引入了一些性質, 并再借助這些性質簡要介紹了本研究領域的發展現狀及相關結論。
主要性質
(1)性質,設f是定義在[a,b]上的函數,a<c<b, 則f在[a,b]上可積的充分必要條件是f在[a,c]和[c,b]上都可積, 此時
它表示曲線y=f(x)與直線x=a,x=b和y=0圍成的圖形面積的代數和。
(2)性質設f在[a,b]上連續, 則至少存在一點∈[a,b], 使得
四、主要結果
本文主要論證的是積分在數列求和中的應用, 下面通過舉例闡述應用。
1.積分在數列求和中的應用


通過上述例子說明, 利用積分直接計算數列的和的問題, 是一種較好的解題方法, 同時, 也使我們認識到初等數學與高等數學之間的內在聯系。
2.積分在幾何, 經濟中的應用
解 利用參數方程
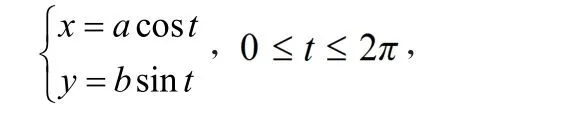
與對稱性得

例2 某公司投資2000萬元建成一條生產線投產后, 在時刻t的追加成本和追加收益分別為(百萬元/年)和=1 7(百萬元/年), 試確定該生產線在何時停產便可獲得最大利潤?最大利潤是多少?
解t時刻的利潤

由極值存在的必要條件可知取得最大利潤的時刻即最大停產時刻, 應滿足L′(t)=0,得,
故生產在投產8年時可獲最大利潤, 其毛利潤為

考慮到固定成本是2000萬元, 可得最大凈利潤
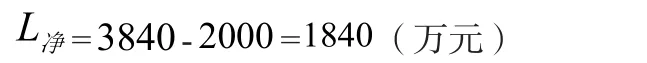
通過上述三例說明, 積分在不同學科內的應用, 是一種較好的解題方法, 同時, 也使我們認識到積分與其他學科之間的內在聯系。

