一種有效的基于GraphX的分布式結構化圖聚類算法*
時生樂,趙宇海,李 源,印 瑩,王國仁
東北大學 計算機科學與工程學院,沈陽 110819
1 引言
圖模型強大的表達能力,使其在社交、化學、生物等領域有著廣泛的應用,例如在社交領域,使用圖模型進行建模,將數據用一個圖來表示,圖中的頂點表示個體,邊表示個體與個體之間的關系。隨著圖應用的不斷增長,人們對圖數據分析和管理中的基本問題進行了大量研究,其中發現聚類或社區結構是圖數據分析中最重要的任務之一,通過發現數據中潛在的結構,人們可以從海量數據中提煉出有價值的信息。例如在社交網絡中,通過對社交網絡進行聚類分析,可以找到網絡中的社區,進而可以分析社區中人們的行為并向對該社區感興趣的人推薦社區。
在當前文獻中,已經提出各種各樣的圖聚類算法,例如基于模塊性的圖聚類算法[1]、k-core算法[2]、kedge算法[3]、k-truss算法[4]、譜聚類算法[5]和局部密集子圖發現算法[6]等。然而上面這些算法都不能區分一個圖中頂點的不同角色,而對圖中頂點的角色進行區分在現實中有重要應用。為了能夠區分圖中頂點的不同角色,Xu等人第一次提出結構化圖聚類算法[7]。該算法使用圖中頂點之間公共鄰居作為聚類條件對圖進行聚類,并且同時將圖中的頂點分為聚類中的點、中心點、離群點3類。其中,聚類中的點指算法找出的每個簇中的頂點,中心點指橫跨兩個及兩個以上聚類的頂點,離群點指除聚類中的頂點和中心點之外的其他頂點。例如在圖1中,通過結構化圖聚類算法找到圖中的兩個聚類:由頂點v1~v8組成的聚類1,頂點v10~v15組成的聚類2(分別用虛線圈出);同時也找到了連接聚類1和聚類2的中心點v9和離群點v16、v17、v18。
結構化圖聚類在實際生活中有重要應用。例如,如果將圖1看作用于傳染疾病防控的圖數據,圖中的每個頂點表示一個人,頂點之間的連線代表人與人之間的接觸關系。在傳染疾病爆發時,如果能夠找到連接群體之間的關鍵人物(例如頂點v9),并對其隔離,就能夠有效阻止傳染疾病在群體之間進行傳播,對疾病的防控具有重要意義。

Fig.1 Structural graph clustering圖1 結構化圖聚類
本文通過對結構化圖聚類中頂點間相似性定義和基于Hadoop[8]的MapReduce分布式結構化圖聚類算法進行分析,提出一種基于GraphX[9]的分布式結構化圖聚類算法。
本文主要貢獻如下:
(1)通過對結構化相似性定義的分析,找到一種減少圖中頂點之間結構化相似性計算數量的削減策略;
(2)通過對結構化相似性計算過程的分析,提出一種通過非精確計算頂點之間相似性來確定頂點之間是否相似的方法;
(3)通過發現現有分布式結構化圖聚類算法在計算過程中需要大量磁盤I/O開銷的不足,提出一種基于GraphX的結構化圖聚類算法消除計算過程中的磁盤I/O開銷。
本文剩余部分組織如下:第2章闡述和分析了分布式圖聚類的相關工作;第3章對分布式結構化圖聚類問題和相關概念進行定義;第4章詳細闡述本文提出的基于GraphX的結構化圖聚類算法;第5章通過對比實驗分析算法的效率和可擴展性;第6章對全文進行總結。
2 相關工作
近年來,隨著社交網絡、生物、醫學等領域的快速發展,產生大量大規模圖數據集,由于內存限制,使得傳統基于單機的圖聚類算法[1,7,10]已經不能夠處理這些大規模圖數據集,因此基于分布式的圖聚類算法不斷出現。
分布式的圖聚類算法[11-12]主要思想是將圖數據集按照一定規則分布到集群的各個結點上,然后在各個結點處理一部分數據集,在計算過程中只涉及結點間的網絡通信,不需要磁盤I/O開銷,且可以根據數據集的規模任意添加機器,可擴展性好,理論上可以處理任意規模的數據集。因此開發分布式的圖聚類算法是圖挖掘研究的重點之一。
由于結構化圖聚類算法能夠識別出頂點的不同角色,因此在圖分析中扮演著重要角色,文獻[13]是目前最具代表性的圖聚類算法之一,但是該算法存在大量磁盤I/O開銷和大量精確計算頂點之間結構化相似性等問題。
隨著分布式計算技術的快速發展,目前已經出現了以Hadoop[8]和Spark[14]為代表的分布式系統,并在商業和研究中得到廣泛應用。Hadoop具有高可靠、高擴展、高容錯等優點,是目前商業領域使用最多的分布式系統之一。但Hadoop也有磁盤I/O開銷大、對圖計算和迭代計算支持不好等缺點。Spark是一個開源的分布式內存計算框架,GraphX是Spark上的一個專門用來進行圖計算的彈性分布式圖系統。GraphX通過Spark將數據并行和圖并行有效結合起來,極大提高了圖計算的存儲和執行效率,且GraphX中內置許多對圖進行計算的原子操作,極大地方便圖計算應用程序的開發。和Hadoop相比,Spark對迭代計算和圖計算的支持更加好,而在圖計算中像kcore、PageRank[15]等許多算法都需要迭代計算,這使得基于GraphX實現的圖算法執行效率將會得到極大提升。
3 問題描述
3.1 相關定義
本研究主要聚焦于無向無權重圖G=(V,E),其中V表示圖G中所有頂點的集合,E表示圖G中所有邊的集合,用|V|=n表示圖中頂點個數,|E|=m表示圖中邊的條數,(v,w)∈E表示兩個端點為v和w的邊,Nv、Nw分別表示頂點v和w鄰居頂點的集合。
定義1(結構化鄰居)對于圖G中任意一個頂點v∈V,頂點v的結構化鄰居定義為:H[v]={w|(v,w)∈E}?{v}。
例如,在圖2中頂點v6的結構化鄰居為H[v6]={v4,v5,v6,v7,v8,v11},頂點v7的結構化鄰居為H[v7]={v6,v7,v8,v9,v10,v11}。

Fig.2 Simple example圖2 一個簡單示例
定義2(結構化相似性)對于圖G中任意兩個頂點v,w∈V,頂點v、w的結構化相似性定義為:

其中,|H[v]|、|H[w]|分別表示頂點v和w的結構化鄰居的個數。
例如在圖2中,頂點v6和頂點v7的結構化相似性為:

給定一個相似性閾值ε(0<ε≤1),如果頂點v和頂點w的相似性閾值δ(v,w)≥ε,則稱頂點v和頂點w是相似的。例如在圖2中,設定相似性閾值為ε=0.8,頂點v6和v7相似性為δ(v6,v7)=2/3=0.667<0.8,因此頂點v5和v6不相似;頂點v4和v5相似性為δ(v4,,因此頂點v4和v5相似。
3.2 基于MapReduce的算法
現有分布式結構化圖聚類算法[13](parallel structural clustering algorithm for big networks,PSCAN)的主要思想是給定一個用鄰接列表表示的無向、無權重圖和一個相似性閾值ε(0<ε≤1),返回圖中所有的聚類;該算法首先根據頂點的鄰接列表計算圖中所有鄰接頂點對之間的結構化相似性,然后去掉圖中相似性小于給定閾值ε的頂點對之間的邊,最后找到圖中所有的連通分量,每個連通分量就是所要找的聚類,具體算法如算法1所示。
算法1PSCAN算法
輸入:一個由鄰接列表表示的圖G(V,E),一個相似性閾值ε(0<ε≤ 1)。
輸出:圖G中所有聚類的集合。
1.Mapper階段:
2.for圖中每個頂點v∈Vdo
3.for頂點v的每個鄰居頂點vido
4. ifID(v) 5. 取(ID(v),ID(vi))作為key; 6. else 7. 取(ID(vi),ID(v))作為key; 8. end if; 9. 取頂點v的鄰居Nv作為value; 10. 發送鍵值對(key,value); 11.end for; 12.end for; 13.Reducer階段: 14.得到從Mapper階段發送的鍵值對; 15.for每一個key相同的兩個鍵值對do 16.計算這兩個頂點的相似性e; 17.end for; 18.for圖中的每條邊(v,w)do 19.if頂點v、w的相似性e<εthen 20. 移除邊(v,w); 21.end if; 22.end for; 23.計算連通分量; PSCAN算法偽代碼如算法1所示,在Mapper階段(行1~12),計算每個頂點和它們的每個鄰居組成的鍵值對,使用ID(v)、ID(vi)的升序作為key(行4~8),使用頂點v的鄰居作為value;在Reducer階段(行13~22),計算每條邊(v,w)兩個端點的相似性e,如果e<ε(說明兩個頂點不相似),移除邊(v,w)(行19~21),最后計算圖中的連通分量(行23)。算法使用標記傳播算法來求連通分量,求得連通分量的集合就是最終的聚類結果。 上面算法產生大量的磁盤I/O開銷,且算法需要精確計算圖中所有鄰接頂點對之間的相似性,降低了算法的執行效率。該算法除了執行效率較低外,存在的另一個問題是算法不能夠去掉只有少量頂點組成的聚類(例如有少量頂點組成的clique[16]),因為只有少量頂點組成的聚類在圖分析中沒有什么意義,所以這樣的聚類不應包含在最終結果中。例如在圖1中,使用該算法將找到聚類1、聚類2和由頂點v17和頂點v18組成的聚類,因為根據相似性定義可知,只有兩個頂點組成的聚類頂點之間的相似性恒為1,所以無論ε值為多大,只有兩個頂點組成的聚類始終包含在最終結果中,降低了算法的準確性。 針對第3章PSCAN算法存在產生大量I/O開銷等不足,本文提出一種基于GraphX的分布式結構化圖聚類算法GXDSGC(GraphX-based distributed structural graph clustering algorithm),該算法能夠很好解決上述問題。給定一個無向無權重圖、一個相似性閾值ε(0<ε≤1)和聚類中頂點的最小個數minNum,GXDSGC算法找到圖中所有聚類和由中心點和離群點組成的頂點的集合。下面介紹算法中用到的兩個削減規則。 在現有的PSCAN算法中是計算圖中所有邊所關聯的頂點之間的相似性,頂點之間相似性的計算在整個算法中是一個比較耗時的操作,如果能夠減少圖中頂點之間相似性的計算量就會大大增加算法的執行效率。通過對頂點之間相似性定義進行分析后,得到下面的削減規則。 引理1對于一個給定的相似性閾值ε(0<ε≤1)和兩個頂點v和w,如果|Η[v]|<|Η[w]|×ε2或|Η[w]|<|Η[v]|×ε2,那么頂點v和w不相似。 證明因為|Η[v]|<|Η[w]|×ε2,所以 即δ(v,w)<ε,所以頂點v和w不相似;同理當|Η[w]|<|Η[v]|×ε2時,δ(v,w)<ε。 因此當 |Η[v]|<|Η[w]|×ε2或|Η[w]|<|Η[v]|×ε2時,頂點v和w不相似。 □ 利用上面的削減規則,得到下面判斷兩個頂點不相似的算法。 算法2disSimWithPrune算法 輸入:頂點v和w的結構化鄰居Η[v]和Η[w],一個相似性閾值ε(0<ε≤1)。 輸出:如果不相似輸出true,否則輸出false。 1.if(|Η[v]|<|Η[w]|×ε2or|Η[w]|<|Η[v]|×ε2) 2.returntrue 3.else 4.returnfalse 該算法使用引理1來判斷兩個頂點不相似,如果兩個頂點v和w滿足引理1中的條件,則頂點v和w一定不相似,輸出true,否則不能確定這兩個頂點是否相似輸出false。 計算圖中頂點之間相似性的目的是判斷這兩個頂點是否相似,根據定義需要計算這兩個頂點公共鄰居的個數,在給定相似性閾值ε(0<ε≤1)時,如果能夠找到使得這兩個頂點相似的最小公共鄰居的數目,這樣在求公共鄰居數目時,一旦公共鄰居的個數大于使得頂點之間相似的最小公共鄰居的數目,就不需要再往下計算其他的公共鄰居。為了實現上述思想,本文給出下面的引理。 引理2對于一個給定的相似性閾值ε(0<ε≤1)和頂點v和w的結構化鄰居Η[v]和Η[w],設mincount(v,w)為大于等于的最小整數,即那么頂點v和w相似的充要條件是|Η[v]∩Η[w]|≥(v,w)。 利用引理2,算法3給出在不精確計算兩個頂點相似性的情況下,確定兩個頂點是否相似的算法。 算法3isSim算法 輸入:頂點v和w的鄰居Nv和Nw,用Nv[i]表示頂點v的第i+1個鄰居(其中Nv和Nw中的頂點按照頂點標號的升序排列),一個相似性閾值ε(0<ε≤1)。 輸出:如果頂點v和w相似,輸出true,否則輸出false。 3.counter=2;/*記錄已求公共鄰居的個數*/ 4.i=0;j=0;/*指示數組下標*/ 5.dv=Nv.length;dw=Nw.length; 6.whilecounter 7.if(Nv[i] 8.dv=dv-1;i=i+1; 9.else if(Nv[i]>Nw[j])then 10.dw=dw-1; 11.j=j+1; 12.else 13.counter=counter+1; 14.i=i+1; 15.j=j+1; 16.end if 17.end while 18.if(counter 19.returnfalse; 20.else 21.returntrue; 22.end if; 算法3中,首先求出使得頂點v和w相似的最小結構化公共鄰居的個數(行1~2);然后定義記錄已求結構化公共鄰居個數的變量counter,因為算法傳入的是頂點v和w的鄰居頂點,算法后面只是求頂點間公共鄰居的個數,并沒包含頂點v和w本身,而算法是求結構化鄰居的公共頂點個數,因此初始化為2(行3);接著初始化指示數組的下標i=0,j=0(行4);定義兩個鄰接列表中除已比較的不相等的鄰接頂點后剩余的頂點的個數,初始化為對應兩個鄰接列表中元素的個數(行5);在while循環中求結構化公共鄰居的個數(行6~17),當求得的結構化公共鄰居的個數大于等于mincount或者除已比較的不相等的鄰接頂點后剩余的頂點的個數du,dv的最小值小于使得兩個頂點結構化相似的最小結構化公共鄰居的最小個數時,沒有必要再求后面的公共鄰居,直接跳出while循環;最后,判斷已求的結構化公共鄰居數counter是否小于mincount,如果小于說明兩個頂點不相似,返回false,否則兩個頂點相似,返回true(行19~22)。 在計算圖中的每個連通分量時,本文使用Pregel框架[17]來分布式計算圖中所有的連通分量。Pregel將計算過程分為一個個超步,計算開始時標記所有頂點為活動狀態。在每個超步中,每個頂點接受上一個超步發送給它的消息后進行處理并更新當前頂點的狀態,更新后當前頂點仍為活動狀態則將處理后的結果發送給下一個超步,否則該頂點什么也不做,當前超步中每個頂點都處理完成后進入下一個超步,當所有頂點都處于非活動狀態時算法結束。下面通過一個簡單的例子來介紹使用Pregel計算連通分量的過程。 如圖3所示,例如,要求值為1、2、3、4的4個頂點組成的連通分量,白色頂點表示該頂點處于活動狀態,灰色頂點表示該頂點處于非活動狀態,實線表示頂點之間的邊,虛線表示向下一個超步中的頂點發送的消息。初始時4個頂點都處于活躍狀態,因此在超步0中,每個頂點都向它的鄰居發送自己的當前值,在超步1中,每個頂點接受超步0發送過來的值,如果接收到的值的最大值比當前頂點值大,則更新當前值為接收的最大值,然后將該頂點標記為活躍狀態并向鄰居頂點發送更新后的值,如果接收到的最大值比當前頂點值小,則將該頂點標記為非活躍狀態。例如,第一頂點收到的值為{2,3},其中收到的最大值3大于當前頂點,因此更新當前頂點值為3,將該頂點標記為活動狀態并向下一個超步發送該頂點的當前值,第4個頂點收到的值為3,小于當前頂點的值4,標記該頂點為非活動狀態,超步2和超步1處理類似,最后在超步3中,由于所有頂點都成為非活動狀態,因此算法結束,值相等的頂點在同一個連通分量中。 Fig.3 Computing connected component圖3 計算連通分量 基于算法2、算法3、連通分量算法,下面給出基于GraphX的分布式結構化圖聚類算法(GXDSGC)。 算法4GXDSGC算法 輸入:一個無向無權重圖G(V,E),一個相似性閾值ε(0<ε≤1),聚類中頂點的最小個數minNum。 輸出:圖G中所有的聚類的集合。 1.求出每個頂點的鄰居頂點; 2.將每個頂點的鄰居頂點作為該頂點的屬性值; 3.for在圖中的每個鄰接頂點對v,wdo 4.if(disSimWithPrune(Nv,Nw))then 5. (v,w).isSim=false; 6.else 7. (v,w).isSim=isSim(Nv,Nw); 8. end if; 9.end for; 10.for(v,w)∈Edo 11.if((v,w).isSim=false)do 12.移除邊(v,w); 13.end if; 14.end for; 15.計算圖G的連通分量; 16.for每個連通分量CCdo 17.ifCC.num 18. 移除CC; 19.end if; 20.end for; 基于GraphX的分布式結構化圖聚類算法(GXDSGC)如算法4所示,算法首先使用GraphX中的兩個函數aggregateMessages和outerJoinVertices求出圖中每個頂點的鄰居頂點并將鄰居頂點作為該頂點的屬性值(行1~2);然后對圖中的每個鄰接頂點對v,w求相似性(行3~9),在求相似性時,首先使用削減規則(算法2)判斷當前頂點v,w是否不相似,如果不相似設置這兩個頂點間的相似性為false(行4~5),否則使用算法3來求這兩個頂點之間的相似性(行7);接著移除圖中所有不相似的鄰接頂點對之間的邊,使用4.3節“連通分量算法”求得圖中所有的連通分量(行15);然后刪除頂點個數小于指定閾值minNum的連通分量;最后求得的連通分量就是所要求的聚類。 本實驗所用的軟硬件環境如下:集群由5臺服務器組成,每臺服務器的配置為:Red Hat 64位操作系統,16核CPU,主頻1.9 GHz,16 GB內存,2 TB硬盤;Hadoop版本為2.6.0,Spark版本為1.6.0,Java版本為1.8.0,Scala版本為2.10.4。 開發環境配置:操作系統為Windows 732位旗艦版,主頻3.10 GHz,4 GB內存,500 GB硬盤;開發工具IntelliJ IDEA Community Edition 15.0.2,Java版本為1.8.0,Scala版本為2.10.4。 實驗數據集:本文使用DBLP、Youtube、LiveJournal 3個真實數據集和人工數據集進行實驗。其中,DBLP是一個作者協作網絡;Youtube是一個用戶到用戶鏈接網絡;LiveJournal是一個在線社交網絡。人工數據集使用文獻[18]中的算法生成。數據集統計信息如表1、表2所示。 Table 1 Real datasets表1 真實數據集 Table 2 Synthetic datasets表2 合成數據集 下面將本文中提出的GXDSGC算法和Zhao等人提出的PSCAN算法[13]進行對比實驗。實驗從運行時間、削減策略和可擴展性三方面來進行比較。PSCAN算法和GXDSGC算法在相同配置的集群上運行,因為PSCAN算法并沒有指定聚類的最小尺寸,所以在實驗中將GXDSGC算法的最小聚類尺寸設置為2,使得兩種算法的結果相同。下面分別從這三方面對GXDSGC算法進行分析。 (1)運行時間 在該實驗中,對于不同數據集,在相似性閾值分別取0.6、0.7、0.8、0.9的情況下,分別運行GXDSGC算法和PSCAN算法。算法在表1中數據集上的運行時間如圖4所示。 從圖4中實驗結果可以看出,在相似性閾值不斷增大情況下,兩個算法的運行時間都逐漸減小,并且GXDSGC算法在4個數據集上的運行時間比PSCAN算法快30多倍,說明該算法和PSCAN算法相比是非常有效的。 GXDSGC算法速度比較快的原因主要有兩個:第一個是GXDSGC算法是基于GraphX的算法,當集群的內存足夠大時,數據在處理過程中整個數據都在內存當中,中間結果也是存儲在內存的,避免了大量的磁盤I/O,節省了大量時間,而PSCAN在Hadoop集群中運行時需要經歷多個Mapper和Reducer階段,即使集群的內存有足夠的空間,在每個階段都需要將中間結果存儲在磁盤中,在下一個階段從磁盤讀取中間結果,極大增加了磁盤I/O開銷,進而增加了程序的運行時間。第二個原因是GXDSGC算法在計算鄰接頂點之間相似性時,通過兩種削減策略來計算頂點之間的相似性,在不精確計算頂點間相似性的情況下,判斷出兩個頂點是否相似,進一步減少了程序的運行時間。 (2)削減策略 為了比較算法中兩個削減規則的有效性,在實驗時,只記錄圖中頂點間相似性計算消耗的時間,對于每個數據集運行5次算法,然后對消耗的時間求平均值,得到結果如圖5所示。 Fig.4 Running time圖4 運行時間 從圖5中可以看出,對于每個數據集,使用削減規則和不使用削減規則相比,使用削減規則計算相似性所花費時間明顯減少,說明算法中削減規則確實減少了相似性計算消耗的時間。從圖5中還可以看出,對于每個數據集,隨著相似性閾值不斷增大,使用削減的算法運行時間不斷減少,這是因為隨著相似性閾值不斷增大,更多的相似性計算通過削減規則計算出來,說明相似閾值越大,削減規則越有效。 為了進一步比較算法中削減規則的有效性,下面實驗使用表2中的合成數據集進行實驗。實驗結果如圖6所示。 Fig.5 Pruning strategy圖5 削減策略 Fig.6 Pruning strategy on synthetic datasets圖6 合成數據集上的削減策略 首先,保持圖中邊條數不變,改變頂點個數,使用削減和不使用削減消耗時間如圖6(a)所示。然后,保持圖中頂點個數不變,改變邊的條數,使用削減和不使用削減消耗時間如圖6(b)所示。從圖6可以看出,無論是改變頂點個數還是改變邊條數,使用削減策略能夠明顯減少相似性計算所消耗的時間。從圖6(a)可以看出,隨著頂點個數增加,兩種算法消耗時間都不斷增大,但使用削減算法增幅較小,因為使用削減策略的算法能夠通過削減策略減少計算時間。從圖6(b)可以看出,在圖中頂點個數不變的情況下,隨著邊條數的增加,沒有使用削減策略計算相似性所消耗時間增加,而使用削減策略算法所消耗時間也增加但增幅較小,因為在頂點個數不變的情況下,隨著邊數的增加,有更多相似性需要計算,所以增加了整個相似性計算時間;對于使用削減的算法,雖然有更多相似性需要計算,但是隨著邊數的增加,頂點鄰居個數會變大,就會有更多之前不能使用削減規則計算相似性的鄰接頂點能夠通過削減策略判斷其相似性,所以隨著邊條數的增加,計算相似性的時間雖然增加但增幅較小。從圖6還可以發現,一個圖越稠密,將會有更多的鄰接頂點能夠通過削減策略判斷其相似性,這樣削減策略就越有效,就能夠明顯減少算法在計算相似性時所消耗的時間,加快計算速度。 (3)可擴展性 在該實驗中,為了比較GXDSGC算法的可擴展性,對于3個真實數據集,GXDSGC算法的相似性閾值設置為0.6,最小聚類尺寸設置為2,實驗結果如圖7所示。圖7(a)表示在改變集群中機器數的情況下GXDSGC算法在各個數據集上的加速比。圖7(b)表示在改變集群中機器數的情況下GXDSGC算法在各個數據集上運行時間的相對加速比。在該實驗中,相對加速比的計算公式為: 從圖7中可以看出,GXDSGC算法具有良好的可擴展性,且隨著數據集規模的增加,算法的加速性能更好,因為隨著圖尺寸的增加,減少集群中機器間的通信開銷在整個運行時間中所占的百分比。從圖7(b)中可以看出,算法并沒有達到理想的相對加速比,因為集群中機器之間需要進行通信和數據交換,增加了運行時間,使得相對加速比比理想加速比要小。 Fig.7 GXDSGC speedup圖7 GXDSGC加速比 SCAN算法利用頂點之間的結構信息不僅能夠對圖進行聚類,還能識別出圖中頂點的不同角色,為用戶提供豐富的信息;而PSCAN算法是SCAN算法在分布式集群上的擴展。本文提出的GXDSGC算法是對PSCAN算法的進一步優化,GXDSGC算法在執行過程中能夠極大減少I/O開銷,并能夠通過使用兩個削減策略減少相似性計算時間,通過實驗表明GXDSGC算法處理數據更加高效,但GXDSGC算法在求連通分量時需要多次迭代,花費大量時間且通信開銷也比較大,如何進一步優化算法,降低求連通分量的時間和通信開銷仍需進一步研究。4GXDSGC算法
4.1 削減規則1
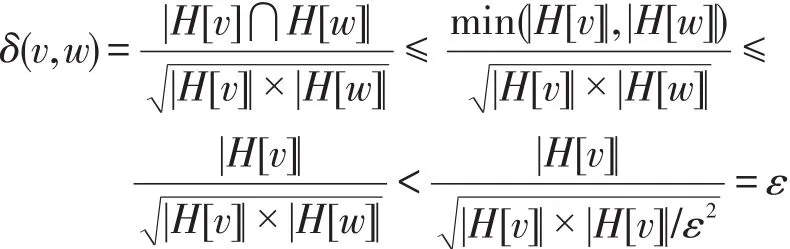
4.2 削減規則2

4.3 連通分量計算

4.4 完整算法描述
5 實驗與分析
5.1 實驗環境配置
5.2 實驗所用數據集


5.3 實驗結果及分析




6 結束語

