彈道導彈發射點位置的彈道重構尋優估計
劉新建,胡佳鑫,楊樂平
(國防科技大學空天科學學院,長沙410073)
0 引言
彈道落點預報是彈道導彈預警和反導中的重要任務,但彈道導彈發射陣地的位置估計在彈道導彈防御中也具有重要作用。對于戰略彈道導彈,要準確判定是哪個敵對國家進行的攻擊,何時何地發射的,以便迅速進行反擊;對于戰術彈道導彈,由于發射也需要調平和方位瞄準,一般是事先安排了有陣地依托的發射,也要盡可能準確知道敵方是何時何地發射的,以便告知偵察衛星對該區域掃描拍照,通過衛星圖像進一步精確鎖定坐標,以便轟炸發射陣地或彈道導彈貯存基地。
Danish[1]較早研究了天基測量戰術彈道導彈(TBM)主動段彈道的發射點參數估計問題;Isaacson等[2]研究了戰術彈道導彈的狀態估計和軌跡預報。國內李盾等[3]基于同步軌道預警衛星對助推段彈道導彈的測量信息,利用改進的高斯-牛頓法探討了發射點參數的最大似然估計,但必須利用主動段目標彈道曲線的先驗信息;宋偉等[4]、陽曙光等[5]研究了雙星交匯測量戰術彈道導彈主動段的彈道參數,并利用多項式擬合進行彈道外推估計發射點參數;王瑞等[6]研究了天基紅外低軌衛星系統對自由段空間目標定位的最小二乘、卡爾曼跟蹤濾波及自適應濾波的方法。但鮮見基于對大氣層外被動段彈道的短弧測量對發射點位置進行估計的研究,而且這種多項式彈道擬合外推發射點的方法較為簡單,對TBM主動段可能有效,但對中遠程、洲際彈道導彈的被動段測量信息反推發射點未必有效。
發射點的位置確定比彈道的落點預報更難,前者是逆問題;后者是正問題,相對要簡單。
本文基于天基或地基設備的被動段短弧測量數據,假設在WGS84系中,得到了來襲彈道導彈大氣層外的部分彈道,提出發射陣地位置估計方法。
1 濾波定軌
(1)坐標參數轉換
假設ti∶xi,yi,zi,vxi,vyi,vzi(i=1,2,…,n)為彈道導彈在真空中的一段短弧軌跡測量數據,分別從WGS84系轉換到某一地心慣性系,如J2000 系,得到ti∶Xi,Yi,Zi,Vxi,Vyi,Vzi。
其中,ti為飛行時刻,Xi、Yi、Zi為彈道導彈在該時刻的3個直角坐標位置分量,Vxi、Vyi、Vzi為該時刻的3個速度分量。
(2)均值濾波去噪
由于每個測量值含有噪聲,并非是彈道導彈的真實狀態,因此需要去噪濾波。工程上有多種數字濾波方法,如卡爾曼濾波、最小二乘濾波、自適應濾波、平均值濾波。特別對于地基雷達,由于地球曲率的影響,可見弧段極短,而彈道導彈飛行速度極快,獲得的測量數據不會很多,因此可采用單點均值濾波。均值濾波最簡單,沒有延遲,對少量的短弧測量數據魯棒可靠。
所謂均值濾波,就是依次利用測量數據ti:Xi,Yi,Zi,Vxi,Vyi,Vzi(i=1,2,…,n),根據真空段自由飛行動力學模型式 (2),進行數值積分,獲得測量數據段之后任選的定軌時刻tf的n個狀態數據。如果測量弧段的數據沒有噪聲,那么依次積分,預報tf時刻的六分量狀態應該是完全相同的;但正因為存在測量噪聲,所以依次積分獲得該時刻的狀態也存在噪聲,那么求平均值。

可是tf時刻的彈道導彈真實狀態只有一個,如果測量數據的噪聲遵循白噪聲分布,而且采樣點足夠多,則平均值逼近真值,就得到了彈道導彈真實狀態tf:Xf,Yf,Zf,Vxf,Vyf,Vzf。
(3)根據如下地慣系中空間飛行器的動力學
微分方程組[7]
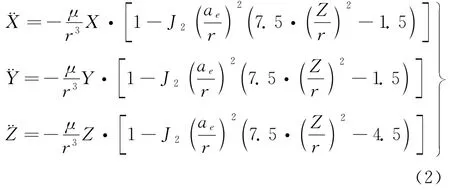
其中,地球扁率J2=1.08263×10-3, 地球引力常數μ =3.986005×1014m3/s2, 地球長半軸=6378140m,地心矢徑再由上述定軌點的真實狀態,進行彈道積分預報再入落點e的直角坐標位置和速度Xe、Ye、Ze、Vxe、Vye、Vze。
2 發射點初始解析估計
為獲得初始估計,不考慮彈道導彈助推段彈道及再入段大氣阻力的影響,假設導彈在地面瞬間獲得足夠能量,滿足測量彈道所預報落點的位置和速度要求,不妨稱為脈沖發射點。脈沖發射點的位置估計是發射陣地位置的近似估計,是彈道重構尋優估計的基礎。
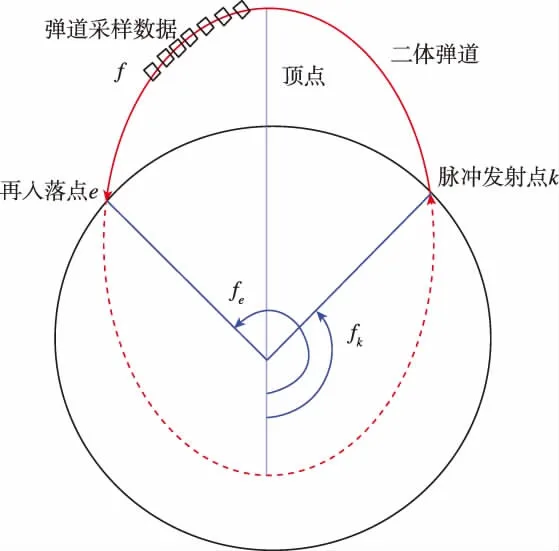
圖1 二體脈沖彈道示意圖Fig.1 Impulse ballistic sketch of two-body problem
1)如圖1所示,根據再入點e的直角坐標和速度Xe、Ye、Ze、Vxe、Vye、Vze, 計算經典軌道根數a、e、i、Ω、ω、M,并求其真近點角fe[8]。
2)求二體脈沖發射點的真近點角fk
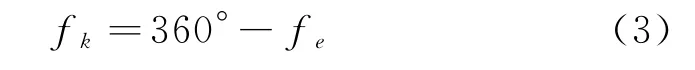
于是不難求得其對應的平近點角Mk和偏近點角Ek。
3)求二體飛行時間
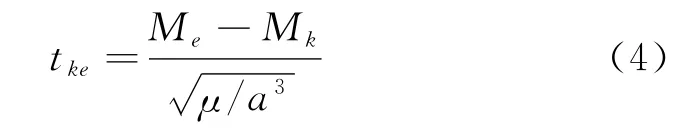
其中,a是定軌得到的彈道長半軸,平近點角Me=M。
4)求脈沖發射點的經緯度
理論上,這是一個已知再入終點位置和飛行時間,反求初始點位置的逆向動力學問題。這里提出利用二體運動軌道的封閉性特點,避開逆向積分問題。
根據二體運動理論,二體脈沖發射點的直角坐標有如下解析公式[9]
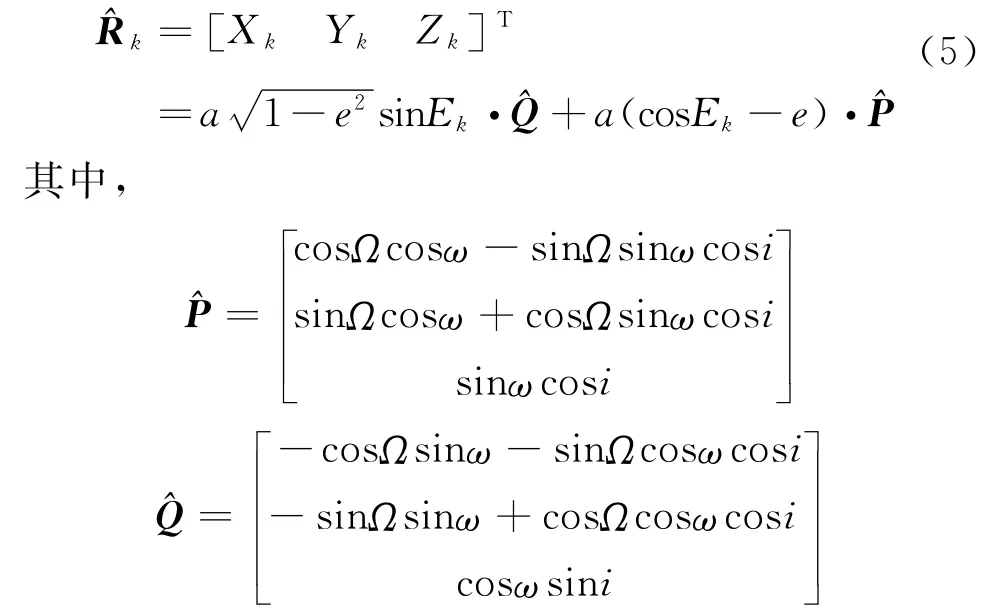
再將其從地慣系轉換到WGS84系的xk、yk、zk,由此計算脈沖發射點的經緯度λk、фk,就是發射點的初步估計,誤差與主動段的彈道設計程序及參數有關,對于射程超過10000km的洲際彈道導彈,數值仿真表明本方法求得發射點最大誤差為200km。
初始解析估計的計算量很小,適合于彈道導彈防御系統實時快速預報,至少能準確告知彈道導彈來自哪個敵對國家。
3 彈道重構尋優估計
由于脈沖點的估計與發射陣地的真實位置存在誤差,需要進一步修正。策略是在脈沖發射點附近進行系列彈道重構,仿真模擬彈道導彈從發射點垂直起飛、主動段程序轉彎、末級瞄準與閉路控制關機,優選出滿足定軌預報再入點約束的重構彈道,輸出所對應的發射點經緯度。
3.1 尋優方法
1)以脈沖發射點及對應的自由段飛行時間為中心,設定經緯度誤差邊界范圍,如±2°(對應440km邊長的正方形),自由段時間偏差,如±100s,劃分三維網格如圖2所示,遍歷搜索可行解與最優解,發射點位置精度與網格大小有關,顯然網格越細,搜索的時間越長。
2)根據脈沖點與再入落點的經緯度,由球面三角公式估計彈道射程。
3)按照射程大小 (洲際、遠程、中程、近程和短程),參考對應的國內外典型彈道導彈的參數,虛擬來襲彈道導彈的動力學仿真參數,如級數、各級的推力、質量、秒流量、燃燒時間以及氣動阻力、升力系數。
4)按照彈道導彈主動段的彈道設計方法,設計轉彎程序如攻角函數、各級轉彎角速率[8]。
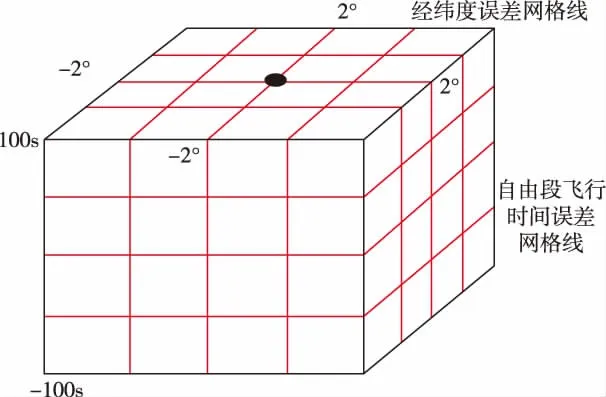
圖2 脈沖發射位置點附近的三維網格Fig.2 Three dimensional grid near impulse launch location
5)為確保再入位置約束,導彈末級采用Lambert制導方法[7],根據末級當前位置矢量,再入落點位置矢量和飛行時間要求,求取需要速度,利用速度增益制導構成閉路關機控制,求得導彈末級飛行的俯仰角、偏航角和關機時間。
3.2 約束條件
以上給出了主要搜索變量的邊界約束和方法,但要模擬真實彈道,還需加入彈道重構約束條件,即仿真彈道的再入點位置和速度六分量應與彈道測量后的定軌值相同或逼近。
再入點位置誤差約束:Δλ≤ελ,Δφ≤εφ,ΔH ≤εH。
即經度、緯度和高程三分量仿真值與定軌值的誤差小于設定值,因為末級采用了Lambert制導方法需要速度閉路制導,仿真會自動滿足,簡化了位置約束的求解。
再入角度誤差約束:ΔΘ≤εΘ,Δσ≤εσ,即速度的傾角和偏角誤差小于設定值
3.3 目標函數
取再入速度模的誤差ΔVe為目標函數,應取最小。
4 仿真驗證
這里以某三級彈道導彈A為例,給出數學仿真予以說明。
(1)導彈A的主要參數[10]
一級起飛質量為34.5t、推力為912kN、工作時間為61s、推進劑秒流量為360kg/s;
二級起飛質量為12t、推力為270kN、工作時間為65s、推進劑秒流量為108kg/s;
三級起飛質量為5t、推力為155kN、工作時間為59s、推進劑秒流量為62kg/s。
末修級工作時間由閉路關機控制指令決定。但彈道數值仿真時,為簡化起見,可不設末修級,第三級工作時間不固定,由閉路關機仿真時間決定,只要滿足自由段飛行時間約束和落點位置約束就可以。其他中短程的戰術彈道導彈類似,也可不設末修級。
(2)發射點和目標點參數假設
發射點:經度-118°,緯度30°;
目標點:經度112°,緯度34°;
兩點之間的射程為11643km。
(3)仿真過程
1)在脈沖估計的基礎上,編寫3自由度仿真優化搜索程序。
2)設計一條從發射點到目標點的標稱攻擊彈道,獲得中段N個短弧采樣數據,例如50個軌跡點,每隔1秒一個采樣數據,適當加入白噪聲,基于這N個數據,完成定軌計算。
3)基于以上方法,完成發射點的二體脈沖估計和彈道重構尋優估計。
(4)仿真結果
二體脈沖估計:
發射點位置誤差
經度差:-0.127°(對應14km)
緯度差:1.0015°(對應110km)彈道重構尋優估計:
發射點位置誤差
經度差:0.125°(對應14km)
緯度差:0.0015° (對應0.2km)
(5)約束條件逼近度
速度誤差:0.047m/s
當地速度傾角誤差:0.85°
速度偏角誤差:0.027°
經度差:0.0045° (對應0.5km誤差)
緯度差:0.0044° (對應0.5km誤差)
圖3給出了上述數值仿真算例的尋優估計重構彈道。
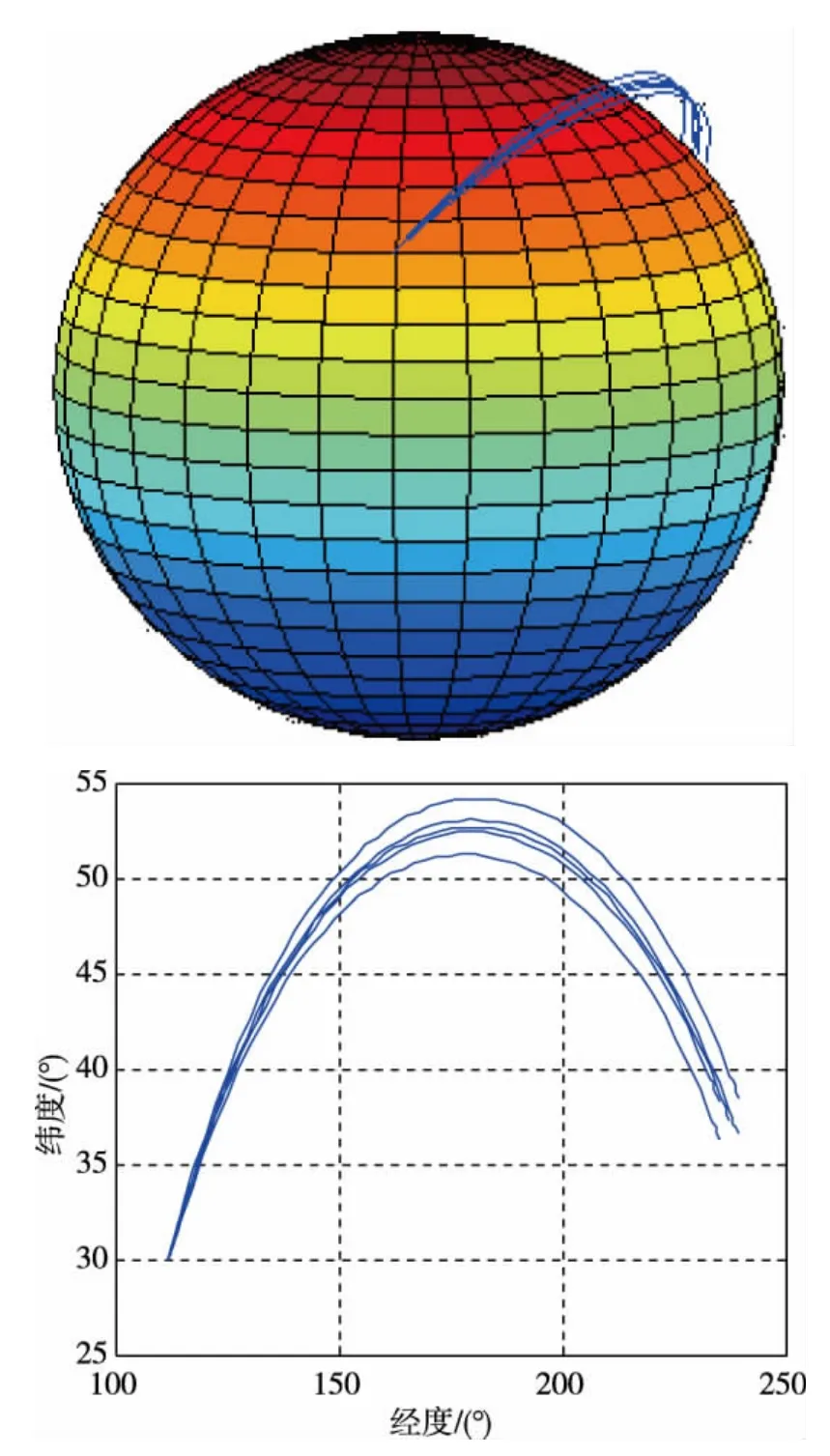
圖3 彈道重構尋優估計數值仿真軌跡示意圖Fig.3 Numerical simulation sketch of optimal estimation with trajectory regeneration
可見,對于本算例的二體快速脈沖估計,發射點的位置誤差為120km,這對于判斷來襲彈道導彈的敵對國家是夠用的。而經過彈道重構的尋優估計,發射點位置誤差估計降到了15km左右,提高了可觀的估計精度,如果發射點尋優網格進一步細分,誤差還可能降低。
5 結論
提出的彈道導彈發射參數估計方法包括脈沖初始估計和彈道重構仿真兩部分,前者實時性好,也是后者的基礎。后者以脈沖點為估計中心,對于戰略彈道導彈,以經緯度±2°誤差為位置邊界,以二體飛行時間tke為中心,±100s為自由段的飛行時間邊界,劃分三維網格,并以再入點的位置三分量、當地速度傾角、速度偏角共5個彈道重構約束條件,以速度誤差為目標函數,進行三自由度彈道控制仿真與優化搜索,求取發射陣地坐標,這樣來減小發射點位置估計誤差。對于戰術彈道導彈,網格邊界可通過仿真進一步縮小,方法類似。
這種彈道重構方法,不需要完全一致的彈道導彈參數,只要大致接近就可,因為是按照彈道導彈攻擊目標所采用的典型彈道規劃方法,基于動力學與控制仿真,并通過優化搜索參數和Lambert末制導來滿足再入邊界條件的,使得數學仿真彈道能夠逼近實際飛行軌跡。
只要獲得了來襲彈道測量參數,本方法可以獲得較高置信度的估計,在彈道導彈預警和防御中有一定參考價值。

