基于Delaunay圖的人工蜂群算法在WSN覆蓋策略中的優化研究

王 軍， 趙子君， 李國強

(沈陽化工大學 計算機科學與技術學院， 遼寧 沈陽 110142)

隨著科學技術的發展和無線傳感器網絡的普及應用，無線傳感器網絡在生活中扮演著越來越重要的角色，特別是在海上監測、森林火災等自然災害方面，災情信息的及時獲取都給我們帶來巨大便利[1].通過在監測區域內投放大量的無線傳感器節點來獲取實時信息，但是由于節點投放的隨機性導致監測區域的覆蓋不均勻，節點分布稀疏的區域就會產生覆蓋漏洞，節點分布過于密集又會產生覆蓋冗余.因此設計一種移動節點調度優化方案來提高覆蓋質量至關重要[2].

目前，傳統的無線傳感器網絡覆蓋問題已經進行了很多研究.Penny等[3]使用改進的粒子群算法指導無線傳感器網絡的部署，在一定程度上提高了網絡覆蓋率，但算法容易陷入局部最優解.文獻[4-5]使用人工蜂群(artificial bee colony，ABC)算法指導網絡布局，但算法收斂速度慢，容易陷入局部最優.Lee 等[6]提出了基于泰森多邊形形心的部署策略(Centroid-Based scheme，CBS)，一定程度上降低了算法復雜度，但網絡覆蓋效果不夠理想.

由固定節點和移動節點共同組成的混合無線傳感器網絡隨機部署在二維目標監測區域可以通過移動節點的位置調整，實現目標區域的優質覆蓋[7].因此，對于傳統人工蜂群算法的缺點，首先利用Delaunay圖尋找覆蓋漏洞，再把改進的人工蜂群算法(Delaunay artificial bee colony，D-ABC)對無線傳感器網絡(wireless sensor networks,WSNs)覆蓋策略進行優化，提高了WSN的整體性能.

1 相關問題

1.1 人工蜂群算法

人工蜂群算法(ABC)是由D.Karaboga[8]于2005年提出的一種人工模擬蜜蜂覓食行為的啟發式智能算法，其優點在于優化過程簡單，控制參數少，易操作.但ABC算法也有啟發式智能算法都有的缺點即過度的隨機性：蜜源初始位置是隨機的；偵查蜂隨機探索新蜜源的位置.以上原因導致蜂群算法后期收斂速度慢，容易陷入局部極值和早熟[9].

1.2 Delaunay圖

1.2.1 Delaunay圖

Delaunay圖即對于一組無線傳感器固定節點，可以得到很多種不用的三角剖分，其中最優三角剖分就是Delaunay三角網[10].體現在其最重要的兩個性質：唯一性，一組點無論如何構造都能得到同一個delaunay三角網；不相交性，delaunay三角網內各邊都不相交.在此根據Delaunay三角網內每個三角形外接圓圓心的位置得到引領蜂的初始位置和個數.還要根據每個delaunay三角形的面積計算每個三角形內部需要部署的偵察蜂個數.

1.2.2 覆蓋漏洞的估算方法

想要確定引領蜂和偵查蜂的位置和個數，首先需要找到Delaunay三角形的外接圓圓心，三角形的外接圓圓心到三角形三個頂點的距離相等，通過比較外接圓圓心到節點的距離與傳感器節點通信半徑的大小關系來判斷三角形內是否存在覆蓋漏洞.

本文研究的是由靜態節點和移動節點組成的混合網絡，由靜態節點在每個三角形內計算覆蓋空洞面積以及計算出移動節點的位置，然后命令移動節點修復覆蓋漏洞.現在需要解決的問題是在每個三角型內判斷是否存在覆蓋空洞，計算覆蓋空洞的面積和移動節點位置信息.

1.3 網絡覆蓋率

網絡覆蓋率指全部傳感器節點覆蓋的總面積占監測區域總面積的百分比[11].在此令So為傳感器節點所覆蓋的總面積，a×b為監測區域總面積，覆蓋率為：

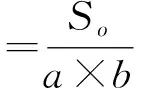
(1)

1.4 感知模型

1.4.1 二元感知模型

二元感知模型也稱布爾感知模型，如果監測節點的感知范圍覆蓋了目標節點，監測概率為1；反之，監測節點的感知范圍沒有覆蓋目標節點，監測概率則為0.這就是所謂的0-1感知模型，又稱之為二元感知模型，最典型的例子當屬圓盤感知模型[12]，如圖1所示.節點o(xo,yo)的感知區域定義為節點o為圓心、以ro為半徑的圓形區域Ro(o,ro)，則位于Ro(o,ro)內的任意點都能被o監測到.其中，ro也被稱作o的感知半徑，且節點的物理特性決定了ro的大小.設平面上任一目標點P(xp,yp)，節點o監測到點p處發生事件的概率表示為：

(2)

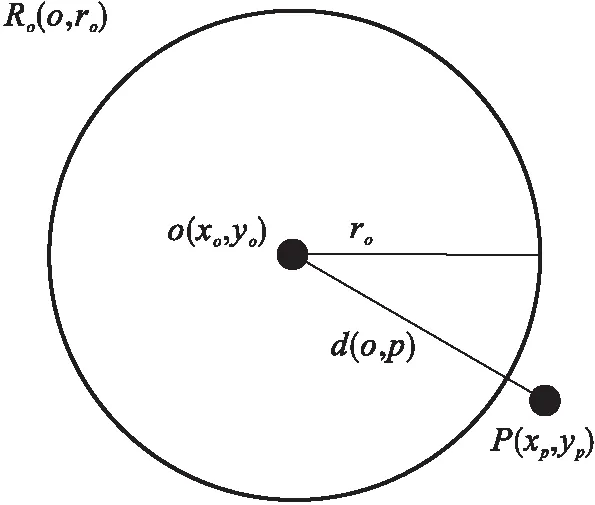
圖1 二元感知模型

1.4.2 概率感知模型

概率感知模型是一種離散的理想模型，符合無線傳感器網絡的真實覆蓋效果，即假定目標點是否被傳感器節點監測到的情況是確定的，也就是監測到設為1，確定不覆蓋設為0.概率感知模型存在一個“中間區域”，即在確定不覆蓋和確定覆蓋中間，如圖2所示.而在實際應用場景中，節點的無線信號由于受到如障礙物、噪聲等外界環境的干擾，概率感知模型反映出節點感知能力隨著距離變化而變化的特征[13].

目標區域內任一目標點p被傳感器節點o監測到的概率表示為:

(3)

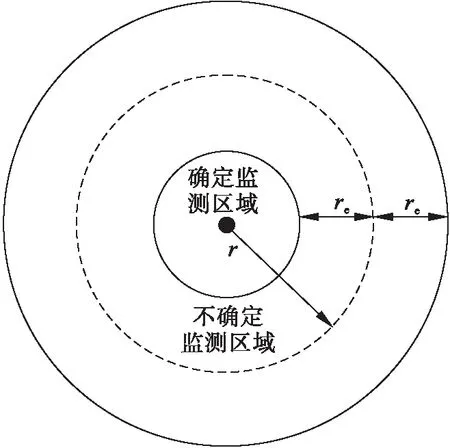
圖2 概率感知模型

2 基于D-ABC的覆蓋優化策略

從蜂群算法的基本原理可知：算法中每個食物源與引領蜂的位置和數量一一對應，偵查蜂圍繞引領蜂進行局部搜索.移動節點的個數等于引領蜂的個數與偵查蜂的個數之和.

2.1 Delaunay三角網覆蓋漏洞的估算

根據討論三角形外接圓圓心到節點距離與節點通信半徑的大小關系來判斷三角形內是否存在覆蓋漏洞.首先求出外接圓圓心So=(Xo,Yo).

(4) 如果三角形的外接圓圓心So(Xo,Yo)到三角形任意一點的距離都小于節點的通信半徑，那么三角形內不存在覆蓋漏洞，反之一定存在覆蓋漏洞.分為以下情況進行討論：

1) 一定不存在覆蓋漏洞

當d(Oi,So)≤Ro時，3個節點的通信半徑覆蓋的面積會兩兩相交，并且一定不存在覆蓋漏洞，如圖3所示.

圖3 不存在覆蓋漏洞

2) 存在覆蓋漏洞情況

A：如果d(Oi,So)>Ro，即O1、O2、O3這3個節點每兩個都不相交而且3個節點到外接圓圓心的距離都大于節點的通信半徑，那么delaunay三角形內一定存在覆蓋漏洞，如圖4所示.可計算出覆蓋漏洞的面積為三角形的面積減去3個扇形的面積之和：

(5)

圖4 情況A:存在覆蓋漏洞

B：如果d(Oi,So)>Ro，并且其中一個節點和另兩個節點相交時，delaunay三角形將會形成鈍角三角形，如圖5所示.由圖5可知：

(6)

那么若想求出S1需先求出兩圓相交面積的一半，用扇形面積SO1C1C2減去三角形面積SΔO1C1C2，計算出d(O1,c)和三角形面積SΔO1C1C2：

(7)

兩圓相交的面積SC1C2C2C1和S1為：

(8)

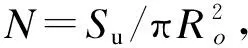
圖5 情況B:存在覆蓋漏洞

2.2 引領蜂的產生

在傳統ABC算法中，蜜源初始位置是隨機的，引領蜂的搜索過程也是隨機的[14].D-ABC算法是根據固定節點的隨機部署情況，生成固定節點對應的 Delaunay三角網，利用 Delaunay三角網找出固定節點覆蓋漏洞，根據三角形面積確定是否生成蜜源，從而確定是否生成引領蜂；三角形的外接圓圓心的位置即蜜源位置，得到引領蜂的位置.

2.3 偵查蜂的改進

在傳統ABC算法中，偵查蜂隨機尋找蜜源，尋找蜜源的過程對應最優解的過程[15].D-ABC算法蜜源位置即引領蜂的位置，通過判斷覆蓋漏洞的大小，分配偵查蜂的數量.

2.4 矩形內創建delaunay三角網

由于delaunay三角網是一個凸多邊形，不能完整覆蓋整個監測區域，這里在矩形內建立delaunay三角網.如圖6所示.

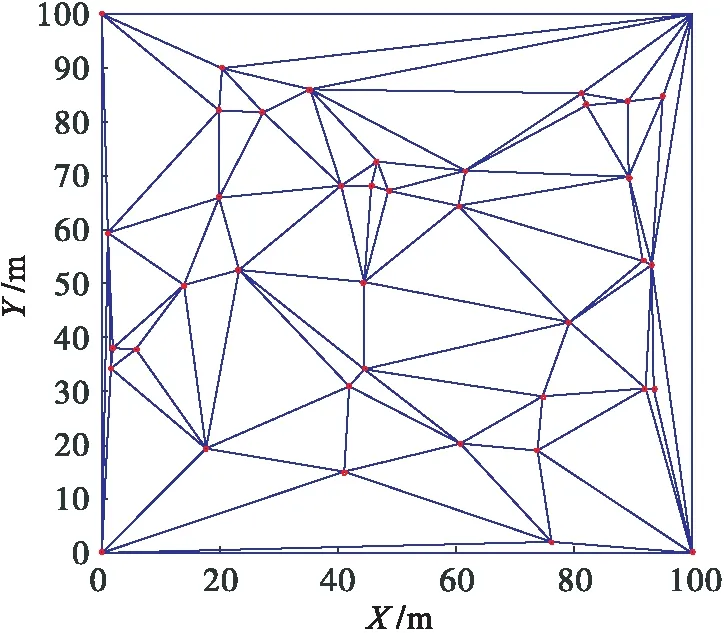
圖6 矩形內的delaunay三角網

2.5 算法執行過程

算法具體步驟如下：

(1) 隨機部署固定節點，并且根據固定節點部署情況生成對應的delaunay三角網.

(2) 通過計算每個delaunay三角形的覆蓋漏洞面積，確定需要填充覆蓋漏洞的delaunay三角形.

(3) 根據delaunay三角形外接圓圓心的數量，初始化引領蜂的數量.

(4) 根據delaunay三角形的面積，確定偵查蜂的數量.

(5) 根據引領蜂和偵察蜂的數量隨機部署移動節點，計算無線傳感器網絡的初始覆蓋率.

(6) 根據delaunay三角形外接圓圓心的位置，初始化引領蜂的位置.

(7) 偵查蜂進行delaunay三角形內部的局部搜索，計算有限次后，停止局部搜索.

(8) 記錄移動節點的最終位置并且生成最終的網絡覆蓋圖并計算網絡覆蓋率.

3 仿 真

建立100 m×100 m的正方形仿真區域，初始條件下隨機放置40個固定節點.由固定節點構成的delaunay三角網計算得到需要的31個移動節點(20個引領蜂和11個偵查蜂).得到初始情況的隨機部署，如圖7所示.網絡覆蓋率為73.63 %.使用D-ABC算法后，網絡覆蓋率為95.71 %.如圖8所示.

圖7 初始部署狀態

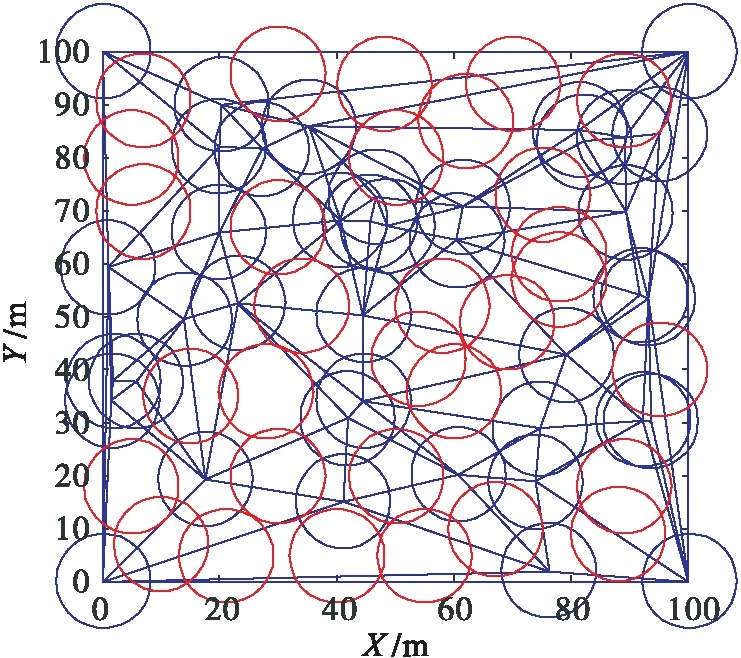
圖8 優化后部署狀態

為更好地體現D-ABC算法的性能，與其他的群智能算法進行對比.在Matlab中對蜂群算法(ABC)、混沌蜂群算法(CABC)、和D-ABC算法的網絡覆蓋率進行了對比，3種算法的迭代次數與網絡覆蓋率的折線圖如圖9所示，可以直觀看出：ABC算法最終可達到的網絡覆蓋率為90.11 %，CABC算法可達到93.48 %，CABC算法相較于ABC算法收斂速度更快，網絡覆蓋率有明顯提高[16]，D-ABC算法相較于CABC收斂速度更快并且網絡覆蓋率可達到95.71 %.

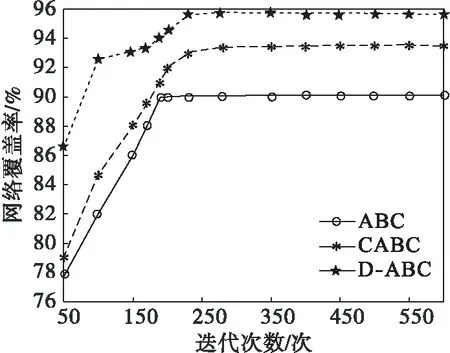
圖9 ABC、CABC、D-ABC算法對比

4 結束語

覆蓋問題是無線傳感器網絡中的基本問題.本文在傳統的人工蜂群算法的基礎上結合delaunay三角網算法提出D-ABC算法，用于解決無線傳感器網絡的節點覆蓋不均勻，覆蓋率低等問題.D-ABC算法能夠快速估算覆蓋漏洞的大小，并且提高網絡覆蓋效率，實現無線傳感器網絡的覆蓋優化.本文目前解決了混合無線傳感器網絡覆蓋中的區域覆蓋問題，需要進一步研究柵欄覆蓋問題，以及在此過程中的移動路徑和節點能量消耗等問題，完成完整的無線傳感器網絡部署.