基于拉普拉斯中心性和密度峰值的無參數聚類算法

邱保志，程 欒

(鄭州大學 信息工程學院，鄭州 450001)

0 引言

聚類是將相似的數據對象聚集在一起，而相異的數據對象盡可能地分離[1]。聚類技術在數據挖掘、模式識別、圖像處理、信息檢索等領域有著廣泛的應用，是數據分析的基礎。在現有的聚類算法中，基于聚類中心的聚類算法由于其應用廣泛而備受人們的關注，例如K-means[2]、具有噪聲的基于密度的聚類方法(Density-Based Spatial Clustering of Applications with Noise, DBSCAN)[3]、密度峰值聚類(Clustering by fast search and find of Density Peaks, DPC)算法[4]等，這些算法都是以選擇初始聚類中心作為聚類的起始點，通過迭代或擴展進行聚類。選擇聚類中心的準確性對聚類的迭代效率、聚類個數的確定和聚類精度有著重要的影響，如何準確地選擇聚類中心、提高聚類精度成為聚類技術研究的關鍵問題。

以K-means為代表的基于劃分的聚類首先初始化聚類中心，然后通過聚類中心的反復迭代的方式進行聚類，這類算法由于初始聚類中心選擇的任意性，導致聚類結果精度不高；以DBSCAN為代表的基于密度聚類的算法是以任一個核心點作為聚類的起始點，將密度可達的對象集合看作一個聚類[5]，由于其中心點選擇的隨意性和密度定義的全局性，造成該類聚類算法不能對多密度數據集和高維數據集進行有效的聚類；基于密度峰值的聚類算法DPC以局部密度峰值為聚類中心，將包圍密度峰值的低密度區域看成一個聚類[6-7]，雖然能準確地確定聚類的中心，但在確定密度峰值時需人工選取相應的參數，在沒有先驗知識的情況下，很難確定聚類的中心[8-9]。為了解決DPC算法存在的問題，拉普拉斯中心峰聚類(Laplace centrality Peaks Clustering, LPC)算法[10]將數據集轉換為加權完全圖，通過計算節點拉普拉斯中心性評估每個節點在加權圖中的重要性，并計算一個節點到更高拉普拉斯中心性的節點的相對距離，將擁有較大拉普拉斯中心性且較大相對距離的對象確定為聚類中心，以此來進行聚類，但這一過程需要建立決策圖人工選擇聚類中心。

針對上述問題，本文通過引入圖的拉普拉斯能量，綜合考量每個節點的拉普拉斯中心性和該節點到具有更高拉普拉斯中心性的節點的相對距離，將數據集映射到由數據對象的拉普拉斯中心性和該對象的相對距離組成的二維特征空間中；進而構造決策圖，依據正態分布的“3σ”準則提取聚類中心，從而自動確定聚類中心；最后將非聚類中心點指派到距離最近的數據對象所屬聚類中，完成整個數據集的聚類。

1 相關定義

設數據集D={x1,x2,…,xn}，其中xi=(xi1,xi2,…,xim),i=1,2,…,n，m為數據對象的維度。用wi, j表示數據對象xi和xj之間的歐幾里得距離，首先把數據集轉換為加權完全圖，數據集中每個數據對象作為圖G中的一個節點，數據對象xi和xj之間的歐幾里得距離作為圖G中節點xi和xj之間邊的權值。

定義1 相異度矩陣[10]。設加權完全圖G是由數據集D轉換得到的，則圖G的相異度矩陣記為W(G)，定義如下：

(1)

其中，wi, j為節點xi和xj之間的歐幾里得距離，對任意的1≤i，j≤n都有：wi, j≥0，wi, j=wj,i,wi,i=0。

Z(G)=diag(Z1,Z2,…,Zn)

(2)

定義3 拉普拉斯矩陣[10]。給定加權完全圖G，它的拉普拉斯矩陣定義為:L(G)=Z(G)-W(G)。其中：Z(G)為圖的和對角矩陣，W(G)為圖的相異度矩陣。

定義4 拉普拉斯能量[11]。對于給定數據集D轉換的加權完全圖G，圖G的拉普拉斯能量LEL(G)定義為其拉普拉斯矩陣的特征值的平方和，即：

(3)

其中,λ1,λ2,…,λn是圖G的拉普拉斯矩陣L(G)的特征值。

定義5 拉普拉斯中心性[11]。給定加權完全圖G，刪除節點xi及其所有相連的邊之后的圖記為圖Gi，給定xi∈G，節點xi的拉普拉斯中心性ci定義為：

ci=(LEL(G)-LEL(Gi))/LEL(G)

(4)

LEL(Gi)是刪除節點xi之后圖Gi的拉普拉斯能量。節點的重要性往往體現在該節點被移除之后對圖的拉普拉斯能量的影響，因此可以用圖中刪除某節點后拉普拉斯能量的相對下降來度量一個節點的重要性(中心性)，拉普拉斯中心性越高，則該節點越重要。

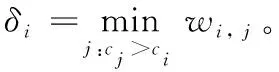
當數據對象xi為聚類中心時，ci和δi具有較大的值，令γi=ci*δi，這時，γi具有較大的值。為了從數據對象中分離出聚類中心，采用式(5)對γi進行放大[12]，加大聚類中心與其他數據對象的差別，從而便于識別真正的聚類中心。

(5)

定義7 正態分布[13]。若隨機變量X服從一個數學期望為μ、標準差為σ的概率分布，且其概率密度函數為:

則這個隨機變量X就稱為正態隨機變量，正態隨機變量服從的分布就稱為正態分布。

在正態分布中，隨機變量X落在(μ-3σ，μ+3σ)以外的概率僅為0.002 7，基本上可以把區間(μ-3σ，μ+3σ)看作是隨機變量X實際可能的取值區間，這稱之為正態分布的“3σ”準則。

當數據對象xi為聚類中心時，該對象具有較高的拉普拉斯中心性ci和較大的相對距離δi兩個特征。潛在聚類中心點所對應的E值遠遠大于非聚類中心點所對應的E值。由于聚類中心點擁有較大的E值，而非聚類中心點的E值較小這一特點，依據正態分布“3σ”準則篩選出那些E值大于μ+3σ的數據對象，將其設為聚類中心。圖1是Sprial數據集所對應的分布直方圖及其正態分布曲線。從圖1中可以看出，Sprial數據集中有3個數據對象的E值大于μ+3σ，這3個數據對象就是數據集Sprial的3個類中心。

圖1 數據集Sprial的分布直方圖和正態分布曲線

2 ALPC描述

基于拉普拉斯中心性和密度峰值的無參數聚類算法(Parameter-free Clustering Algorithm based on Laplace centrality and density peaks, ALPC)首先把數據集轉換為無向完全圖G，得到圖的拉普拉斯矩陣L(G)；然后根據刪除某個數據對象后所引起的拉普拉斯能量變化，來得到數據對象的拉普拉斯中心性ci，并計算得到該數據對象的相對距離δi，接著通過式(5)擴大γ值之間的差別，通過正態分布，選取E值大于μ+3σ的數據對象為聚類中心,然后按照最近鄰分類完成對整個數據集的聚類。ALPC算法描述如算法1所示。

算法1 ALPC。

輸入 數據集D;

輸出 聚類結果。

步驟1 將數據集D轉換為帶權完全圖根據定義1～3計算W(G)、Z(G)和L(G)。

步驟2 根據式(3)、式(4)計算各數據對象的拉普拉斯中心性。

步驟3 提取數據集聚類中心：

a)根據定義6計算各數據對象的相對距離δi；

b)根據式(5)計算各數據對象的E值；

c)運用正態分布的3σ準則，將E值大于μ+3σ的數據對象作為聚類中心。

步驟4 按照最近鄰分類完成對整個數據集的聚類。

在ALPC中，首先需要將待聚類的數據集轉換為帶權的無向完全圖，圖中的每個節點代表數據集中每個對象，利用拉普拉斯中心性來度量對象的重要性。拉普拉斯中心性基本思想是：通過刪除某個節點后所引起的圖的拉普拉斯能量的相對下降來度量該節點的中心性。然后計算該對象到具有更高拉普拉斯中心性的對象的相對距離，在聚類中心選取時，ALPC不再手動選取那些具有較大拉普拉斯中心性和較大相對距離的數據對象作為聚類中心，而是采用概率統計中正態分布理論選取聚類中心，避免了手動選取聚類中心時因視覺誤差所帶來的聚類結果的不準確問題。ALPC綜合考慮對象的拉普拉斯中心性和該對象到更高拉普拉斯中心性的對象的相對距離，通過式(5)加大潛在聚類中心與待聚類數據集中其他對象的差別，利用概率統計中的正態分布理論選取具有較大E值，即E值大于μ+3σ的數據對象為聚類中心,然后按照最近鄰分類原則將其余的點分配到相應的聚類中心，從而完成聚類并輸出聚類結果。

3 實驗結果與分析

該算法的實驗環境為：CPU為AMD 3.4 GHz，4 GB內存，操作系統為Windows 7(64 bit)，算法的編寫使用Matlab R2014a軟件。

3.1 實驗數據集及評價指標

實驗選用 10個數據集，其中 4個人工數據集分別用于驗證ALPC識別橋接簇、螺旋形、球形簇和非球形簇的能力；6個真實數據集來源于 UCI機器學習數據庫，用于驗證ALPC對高維數據處理的有效性。表1詳細描述了實驗數據集的基本信息。

表1 實驗數據集基本信息

實驗的評價指標采用準確率(ACCuracy, ACC)[10]、調整蘭德系數(Adjusted Rand Index，ARI)[5]和歸一化互信息(Normalized Mutual Information, NMI)[5]度量ALPC聚類的有效性。準確率衡量聚類結果與實際結果的符合程度，其取值范圍為[0,1],當算法的聚類結果與真實情況完全一致時準確率為1，兩者越不一致，準確率越低；調整蘭德系數的計算需要待聚類數據集的真實分類結果，其取值范圍為[-1,1]，調整蘭德系數越高意味著算法的聚類結果與數據集的實際分類情況越吻合，從廣義的角度看，調整蘭德系數衡量的是算法聚類結果與數據集實際分類情況的吻合程度；歸一化互信息是衡量聚類結果與數據集實際分類情況的相近程度，同樣需要待聚類數據集的真實分類結果，歸一化互信息的取值范圍為[0,1]，值越大意味著聚類結果與真實情況越相近，聚類效果越好。

3.2 聚類結果分析

首先在二維數值屬性數據集上與DBSCAN、DPC和LPC算法進行聚類有效性的比較，然后在高維數據集上與DBSCAN、DPC和LPC算法進行聚類有效性的比較。

圖2依次是DBSCAN、DPC、LPC和ALPC在4k2_far、Aggregation、Spiral和Ring數據集上的聚類結果，不同的灰度值代表不同的聚類。

圖2(a)是DBSCAN算法的聚類結果，它在Aggregation和Ring數據集上的聚類結果不正確，說明DBSCAN算法不能識別橋接簇和非球形簇，這是因為DBSCAN算法的半徑閾值和密度閾值定義的全局性，當待聚類數據集的密度不均勻、聚類間距差很大時，參數選取困難，半徑閾值和密度閾值選取不合適會造成聚類結果的不準確；圖2(b)是DPC算法在4個人工數據集上的聚類結果，它在Ring數據集上的聚類結果不正確，這是因為DPC算法需要人工輸入截斷距離和手動選取聚類中心，截斷距離定義的全局性和視覺誤差造成的聚類中心選取不準確，就會影響聚類結果的準確性；圖2(c)是LPC算法的聚類結果，它在4k2_far數據集上聚類結果不正確，這是因為LPC算法人為分析決策圖，手動選取聚類中心時視覺誤差造成的聚類中心選取不準確，使聚類結果不準確；圖2(d)是算法ALPC的聚類結果，表明ALPC可以準確識別出數據集中的球形簇、橋接簇、螺旋形和非球形簇。上述四個二維數據集上的聚類結果驗證了ALPC的有效性。

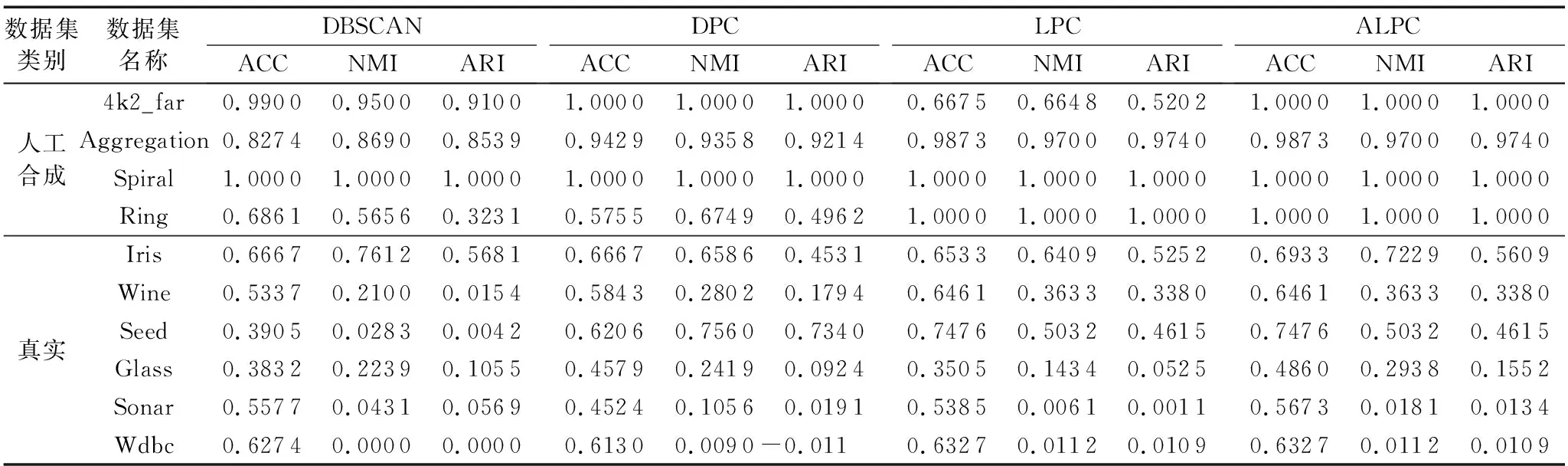
表2給出了4種算法在人工數據集和真實數據集上的實驗結果。從表2中可以看出：與其他三個算法相比，ALPC的ACC值有10項為最高，NMI值有7項為最高，ARI值有7項為最高;雖然ALPC在Iris、Seed和Sonar這三個數據集上的歸一化互信息和調整蘭德系數不是最高值，但與評價指標最高值接近。

ALPC對于Spiral、Ring和4k2_far這三個數據集的執行能力最好，其聚類結果完全正確；與LPC算法相比較，ALPC在不需要人為干預的情況下對于Spiral、Aggregation、Ring、Wine、Seed和Wdbc這六個數據集自動劃分的效果與人為劃分效果一致，實現了自動聚類的目標；ALPC對4k2_far、Iris、Glass和Sonar這四個數據集自動劃分的聚類結果的精度比LPC算法人為劃分的聚類結果的精度要高，說明ALPC在應對一些數據集時，具有更優秀的性能，能得到較好的聚類效果。綜上所述，ALPC對人工數據集和真實數據集均有良好的聚類結果。

3.3 時間復雜度分析

對于對象數量為n的數據集D:1)DPC算法的時間復雜度主要來自于距離矩陣、局部密度和相對距離的計算過程，其中計算距離矩陣和相對距離的時間復雜度為O(n2)，計算局部密度需要依次尋找與該對象相對距離小于截斷距離的對象的時間復雜度最壞為O(n2)，所以DPC算法的時間復雜度為O(n2)。2)DBSCAN算法的時間復雜度為O(n2)；LPC算法的時間復雜度主要來自于距離矩陣、拉普拉斯中心性和相對距離的計算過程，其中計算距離矩陣和相對距離的時間復雜度為O(n2)，計算對象拉普拉斯中心性需要依次刪除該對象并計算拉普拉斯能量的相對下降，時間復雜度最壞為O(n3)，所以LPC算法的時間復雜度為O(n3)。3)ALPC與LPC算法類似，所以ALPC算法的時間復雜度同樣為O(n3)。

LPC算法不需要人工輸入參數，但仍然需要人工選取聚類中心，雖然ALPC和LPC算法的時間復雜度相同，但ALPC可以自動選取聚類中心，避免了人工選取聚類中心的不準確問題。

圖2 4種算法在人工數據集上聚類結果比較

數據集類別數據集名稱DBSCANACCNMIARIDPCACCNMIARILPCACCNMIARIALPCACCNMIARI人工合成真實4k2_far0.99000.95000.91001.00001.00001.00000.66750.66480.52021.00001.00001.0000Aggregation0.82740.86900.85390.94290.93580.92140.98730.97000.97400.98730.97000.9740Spiral 1.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.0000Ring0.68610.56560.32310.57550.67490.49621.00001.00001.00001.00001.00001.0000Iris0.66670.76120.56810.66670.65860.45310.65330.64090.52520.69330.72290.5609Wine0.53370.21000.01540.58430.28020.17940.64610.36330.33800.64610.36330.3380Seed0.39050.02830.00420.62060.75600.73400.74760.50320.46150.74760.50320.4615Glass0.38320.22390.10550.45790.24190.09240.35050.14340.05250.48600.29380.1552Sonar0.55770.04310.05690.45240.10560.01910.53850.00610.00110.56730.01810.0134Wdbc0.62740.00000.00000.61300.0090-0.0110.63270.01120.01090.63270.01120.0109

4 結語

本文應用拉普拉斯理論和正態分布的“3σ”準則，提出了一種無參數聚類算法，實現了聚類中心的自動選擇和無參數聚類，解決了LPC算法人工選取聚類中心的不準確性問題，為基于中心的聚類技術的聚類中心選取提供了理論基礎，提高了聚類精度。

[4] RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks [J]. Science, 2014, 344(6191): 1492-1496.

[5] 邱保志,唐雅敏.快速識別密度骨架的聚類算法[J].計算機應用,2017,37(12):3482-3486.(QIU B Z, TANG Y M. Efficient clustering algorithm for fast recognition of density backbone [J]. Journal of Computer Application, 2017, 37(12): 3482-3486.)

[6] 蔣禮青,張明新,鄭金龍,等.快速搜索與發現密度峰值聚類算法的優化研究[J].計算機應用研究,2016,33(11):3251-3254.(JIANG L Q, ZHANG M X, ZHENG J L, et al. Optimization of clustering by fast search and find of density peaks [J]. Application Research of Computers, 2016, 33(11): 3251-3254.)

[7] 馬春來,單洪,馬濤.一種基于簇中心點自動選擇策略的密度峰值聚類算法[J].計算機科學,2016,43(7):255-258.(MA C L, SHAN H, MA T. Improved density peaks based clustering algorithm with strategy choosing cluster center automatically [J]. Computer Science, 2016, 43(7): 255-258.)

[8] BIE R, MEHMOOD R, RUAN S S, et al. Adaptive fuzzy clustering by fast search and find of density peaks [J]. Personal and Ubiquitous Computing, 2016, 20 (5): 785-793.

[9] XU J, WANG G, DEND W. DenPEHC: density peak based efficient hierarchical clustering [J]. Information Sciences, 2016, 373(12): 200-218.

[10] YANG X H, ZHU Q P, HUANG Y J, et al. Parameter-free Laplacian centrality peaks clustering [EB/OL]. [2017- 12- 05]. https://www.researchgate.net/publication/320602767_Parameter-free_Laplacian_centrality_peaks_clustering.

[11] QI X, FULLER E, WU Q, et al. Laplacian centrality: a new centrality measure for weighted networks [J]. Information Sciences, 2012, 194(5): 240-253.

[12] YE X, LI D, HE X. An algorithm for automatic recognition of cluster centers based on local density clustering [C]// Proceedings of the 2017 29th Chinese Control and Decision Conference. Piscataway, NJ: IEEE, 2017: 1347-1351.

[13] STEIN C M. Estimation of the mean of a multivariate normal distribution [J]. Annals of Statistics, 1981, 9(6): 1135-1151.