基于Nystr?m方法的偏好特征提取
楊美姣,劉驚雷
(煙臺大學 計算機與控制工程學院,山東 煙臺 264005)
0 引言
近幾年,核方法已經成功地應用于各種現實世界中,尤其是那些具有高度復雜性和非線性結構的問題中。核方法已經被廣泛地應用于各種機器問題,如分類、聚類和回歸學習中。在基于核的學習中,輸入的數據點被映射到高維的特征空間中,并將內部成對的數據存儲在一個對稱的半正定核矩陣中。核矩陣的核心作用是描述樣本數據之間的相似性,目前在流形學習和降維中被廣泛應用[1]。在實際應用中矩陣的規模往往較大,因此需要降低矩陣的規模,即對矩陣進行采樣,將高維矩陣映射到一個低維子空間中,然后對低維空間中的矩陣進行分解,這樣做不僅能減小矩陣的規模,解決矩陣溢出的問題,而且還能提高運算的效率。低秩矩陣分解和核學習是構建高級學習系統的兩種有效的方法[2],這兩種方法都可以降低大規模矩陣的計算成本。
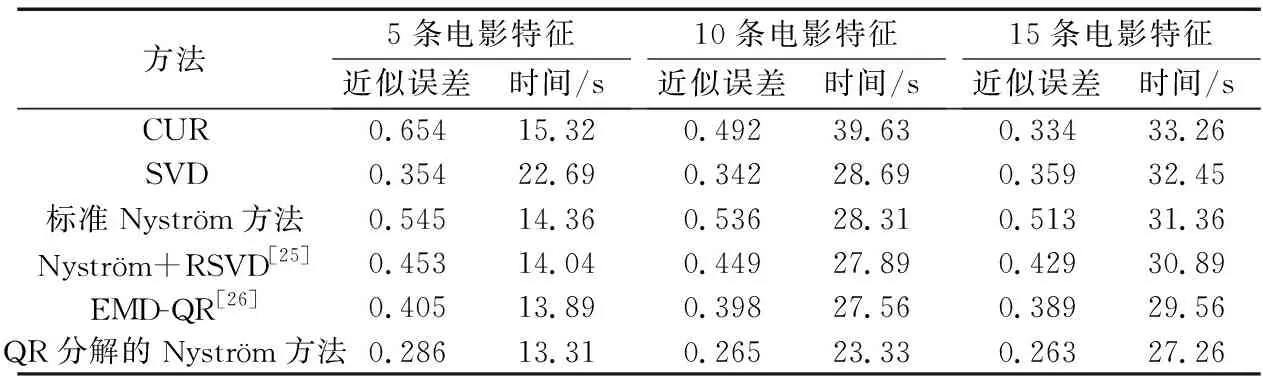
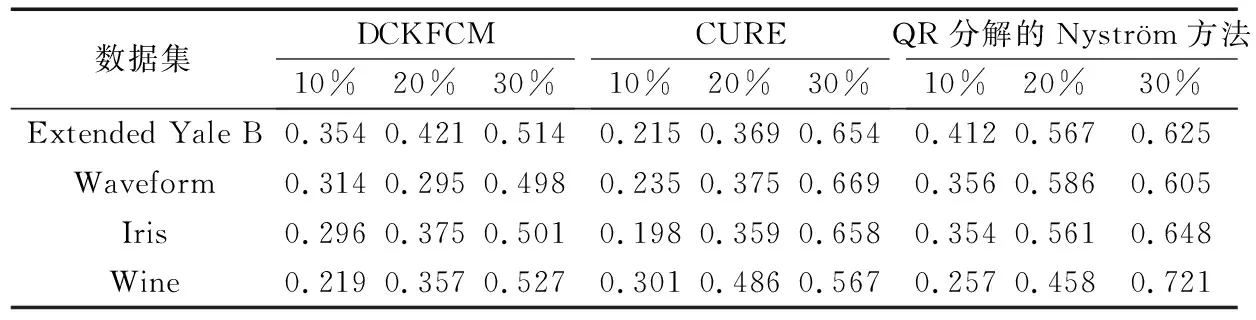
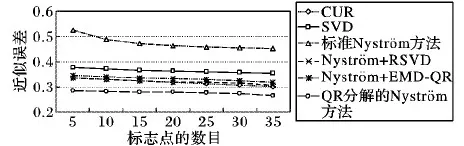
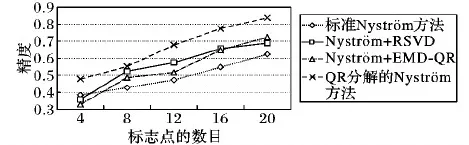
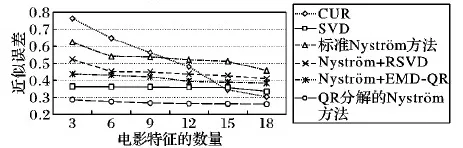
給定一系列n個點, 假設核矩陣K的大小為n×n。核矩陣K≈LLT,其中矩陣L∈n×k,秩k Nystr?m方法的原理是選擇一組“地標點”(有標志性的點),然后計算輸入數據點和標志點的內核相似矩陣[5]。Nystr?m方法的衡量標準與標志點的選取密切相關,若選取的標志點具有普遍代表性,則其相似性越高。原始的Nystr?m方法是從輸入的數據點中隨機地選擇標志點[6],隨機采樣有很多不確定性,使得原始Nystr?m方法的精度并不是很高。本文中將Nystr?m方法與QR方法相結合,即將Nystr?m方法的內部矩陣C進行QR分解,將分解后得到矩陣Q和R,利用分解后的矩陣R和Nystr?m方法的內部矩陣W+相乘,得到矩陣RW+RT,隨后對矩陣RW+RT進行特征分解,得到矩陣V′、Σ′和V′T3個矩陣,最后得到最佳的Nystr?m近似。 本文主要工作如下: 1)標志點的選取影響著對偏好特征的選擇。為了提高采樣后的Nystr?m方法的精確度,利用自適應的采樣方法,即通過多次遍歷并及時更新抽樣概率,選取有代表性的標志點,隨著遍歷次數的增加,采樣后的誤差會大大減小。與傳統的隨機抽樣相比,自適應采樣的精度會明顯提高,同時也避免了隨機抽樣中標志點選取的偶然性。要保證選取的標志點盡可能包含項目的特征,本文設計了標志點選取的算法,該算法跟傳統的算法相比,精度有了一定的提高。 2)本文中將標準的Nystr?m方法與QR分解相結合,解決了標準Nystr?m方法中內部矩陣受到秩限制的問題。本文中的算法還可以用來描述當標志點的數目超過目標秩k時的最佳k近似,因此,本文提出的算法可以與任意標志點選擇方法相結合來尋求最佳k近似。 3)在真實的觀眾對電影評分的數據集上進行了測試,該電影數據集中包含480 189個用戶,17 770部電影,根據觀眾對電影的評分結果進行偏好特征的提取,并與其他算法如奇異值分解(Singular Value Decomposition, SVD)、行列組合(Column Union Row, CUR)、標準的Nystr?m方法、Nystr?m方法和正則奇異化分解(Regularized Singular Value Decomposition, RSVD)的組合(Nystr?m+RSVD)以及基于范例的低秩稀疏矩陣分解(Exemplar-based low rank sparse Matrix Decomposition, EMD)和QR分解的組合(EMD-QR)方法進行了比較,并選取了凸數據集和非凸數據集進行了實驗,從理論和實驗兩個方面證明了本文所提出的算法的有效性。 本章主要介紹了一些相關的定義和符號,為后面工作中要用到的定義和概念作了相應的描述。 假設矩陣A=[a1,a2,…,an]∈Rm×n是一個n中包含n個數據點的列矩陣。計算特征空間中的內積用到“核函數”,它在原始空間上定義為:Bij=b(ai,aj)=〈Φ(ai),Φ(aj)〉,?i,j=1,2,…,n,其中,Φ:a|→Φ(a)是內核誘導的特征圖。n個映射數據點的所有成對內積存儲在核矩陣K∈Rn×n中,第(i,j)個條目是k(i;j)。高斯和多項式核矩陣是對稱半正定核矩陣的兩個眾所周知的例子[7]。盡管在數據的非線性表示中內核很簡單,但是大規模數據集的內核矩陣的計算和存儲卻很棘手[8]。核矩陣的內存為O(n2),內存和計算成本都是以數據點數量的平方為尺度,而且在后續的學習過程中,核矩陣在計算上也需要花費很大的成本。例如,核主成分分析(Kernel Principal Component Analysis, KPCA)算法需要計算核矩陣的特征值分解[9],標準的算法需要的時間復雜度為O(n3),且需要多次遍歷矩陣K。在其他的基于核的學習方法如核嶺回歸中,計算的時間復雜度為O(n3)。對于規模較大的矩陣,要充分考慮計算計算的時間復雜度。 對于任意一個矩陣A∈m×n,A(j)(j=1,2,…,n)定義為A的第j列向量,相應的A(i)(i=1,2,…,m)定義為A的第i行向量。可以將矩陣A分解為: A=UΛV′ (1) Nystr?m方法首次被提出是用于解決近似積分特征函數的問題,后來被用來處理低階近似的核心矩陣[12]。假設給定一個核函數k(·,·)以及具有底層分布的樣本集p(·),Nystr?m方法旨在解決以下積分: (3) 其中:φi(x)、λi分別是第i個特征值函數和關于p的k(·,·)算子的特征值[13]。假設輸入一個對稱的半正定核矩陣K∈n×n。若矩陣的秩rank(K)=r≤n,即存在一個L∈n×n,使得K=LTL。Nystr?m方法的對象是對稱的半正定矩陣,要使用Nystr?m方法,必須對原始的矩陣進行預處理,將矩陣轉化為對稱的半正定矩陣。本文中,利用采樣方法采取其中的c?n列來產生矩陣B的近似矩陣假設采樣的列數c已給定,重點是用自適應方法選出其中的列。矩陣C表示由這些列組成的大小為n×c的矩陣,矩陣W是一個大小為c×c的矩陣,由這些相互正交的列與矩陣B相對應的行組成。矩陣B是對稱半正定矩陣[12],因此,矩陣W也是對稱半正定矩陣。一般的,矩陣B的行和列可以根據采樣后的結果重新排列,可以將矩陣B和C表示為: (4) (5) 其中:矩陣W是一個大小為c×c的矩陣,矩陣B21的大小為(n-c)×c,矩陣B22是一個大小為(n-c)×(n-c)的矩陣。 (6) Nystr?m方法可以近似為矩陣K的前k個特征值(Σk)和特征向量(Uk)。 (7) 該近似將矩陣K的3個模塊重新組合,B22是矩陣K中W的Schur補。 (8) 矩陣W的SVD的時間復雜度是O(kc2),矩陣乘C的時間復雜度是O(kcn),因此整個Nystr?m近似的時間復雜度為O(kcn)。式(6)又可以表示為: (9) 其中: (10) Nystr?m方法構造矩陣Lnys的時間復雜度是O(pnc+c2k+nck),其中構造矩陣C和W的時間復雜度是O(pnc)。執行矩陣W的部分特征值分解的時間復雜度為O(c2k),而矩陣乘法CVk的時間復雜度為O(nck)。因此,對于k 與標準的Nystr?m方法不同,自適應的Nystr?m是在標準Nystr?m方法上作的進一步改進,即每次采樣后,都將剩余列的概率按照降序排列,取其概率較大的列,能盡可能地表示原始矩陣,改進后的Nystr?m方法能夠與任意標志點選取方法相結合,尋求給定秩數的最佳近似[14]。 Zhang等[20]提出了一種使用k均值聚類產生質心的信息列的算法,該算法已被證明具有良好的精度,這種算法的原理是使用樣本外擴展來生成矩陣B的c個有代表性的列。經過對k均值聚類產生質心的信息列的算法的改進,提出了一種具有較強理論基礎(自適應)的抽樣算法,該方法要求在每次迭代中遍歷矩陣B,這樣可以提高采樣的精度。 定理1 自適應采樣。假設給定任意一個矩陣A∈m×n,從其中選取一系列的列向量來構造矩陣S,則每次采樣都遵循以下分布,第i列被選擇的概率可以表示為: (11) 其中:A(i)來表示矩陣A的第i列。 根據定理1可以設計一個高效的采樣算法,但是該算法有一個特點,首先要對原始矩陣進行遍歷,得到其原始分布概率,然后根據得到的各列的概率進行采樣。 隨著采樣次數的增加,誤差會隨著遍歷次數的增加而減少,因此,多次遍歷對于稀疏矩陣的近似非常重要。 定理2 自適應采樣的數學描述。假設S=S1∪S2∪…∪St表示對矩陣A的列進行采樣后的結果,對于j=1,2,…,t,集合Sj表示的是對矩陣A的s列進行采樣后的結果。第i列被選擇的概率可以表示為: (12) 其中:E1=A,E1=A-πS1∪S2∪…∪Sj-1(A),其中πS(A)表示的是A在S的生成空間上的投影。 自適應采樣方法對稀疏矩陣較為重要,當采樣的矩陣較為稀疏時,尤其是像觀眾對電影評分這樣的大規模的稀疏數據,采用這種方法可以降低計算的復雜度,提高運算效率。 與固定采樣不同,自適應采樣在每次選擇完一組樣本后,都會更新所有樣本的概率[21],最終產生最佳的k秩近似。其基本思想是從列的初始分布開始,從矩陣B中選擇s 對于一個大小為n且標志點數目為c的數據集而言,矩陣C∈n×c和矩陣W∈c×c被重新構造,形成低秩近似矩陣n×n。雖然最終的目標是找到一個秩數不超過k的近似值,但是通常要選擇c>k個有標志性的點,然后限制所得到的近似秩最大值為k[24],這樣做的好處是可以使得近似的精度較高。例如,近似誤差是通過c個有標志性的點引起的總的量化誤差函數。很顯然,標志點選取的數目越多,總的量化誤差就會越小,這樣就可以提高k秩近似的質量。因此,選取一種有效而精確的方法對矩陣來講是非常重要的。 (13) 其中:第2個等號中是將矩陣C∈n×c進行了QR分解,即C=QR,其中矩陣Q∈n×c,R∈c×c;而第3個等式中是對矩陣RW+RT進行特征值分解,即RW+RT=V′Σ′V′T,其中,對角矩陣Σ′∈c×c包含主對角線上按照降序分布的c個特征值,V′∈c×c則是相應的特征向量。QV′∈c×c都是正交的,因為Q和V′都有正交的列: (QV′)T(QV′)=V′T(QTQ)V′=V′TV′ (14) 為了產生標志性的點,首先要產生一個信號矩陣H∈n×n,即兩者出現的概率相同,均為0.5。通過計算矩陣HB來找到其低維框架標準的矩陣的乘法時間復雜度為O(n3)。矩陣的乘法可以并行執行,這樣都可以顯著加速。然后,對投影后的低維矩陣進行k-means聚類,將數據集進行分割: (15) 具體的算法如下: 算法1 基于Nystr?m方法的聚類。 輸入:用戶-電影的評分矩陣A∈Rm×n,標志點的數目c; 1) 調用算法2得到相似矩陣B; 2) 調用算法3得到采樣后的矩陣C; 3) 調用算法4得到主要的特征值和特征向量; 4) 產生一個隨機符號矩陣H; 5) 6) 利用式(15)計算原始空間中的樣本均值; 7) Z=[z1,z2,…,zm]∈p×c; 8) 返回:C∈Rm×c。 算法2 求相似矩陣B。 輸入:用戶-電影的評分矩陣A; 1) 輸入用戶-電影數據集A; 2) returnB; 其中,X=x1,x2,…,xn∈Rn,表示的是觀眾對電影感興趣的屬性個數,樣本的協方差矩陣為M。根據距離公式,可以將觀眾對電影的評分矩陣轉化為用戶(電影)與用戶(電影)的相似度矩陣,即對稱的半正定矩陣。 算法3 基于自適應Nystr?m采樣方法。 輸入:用戶-用戶的相似度矩陣B,采樣的列數c,每次遍歷的列數s; 輸出:采樣后的矩陣C。 步驟1 初始化抽樣點的索引的集合B; 步驟2 對于i∈[1,2,…,t],repeat: 1)Pi← ADAPTIVE-SAMPLING(S); 2)根據pi選取的索引構造Bi; 3)將得到的B∪Bi重新賦值給B; ADAPTIVE-SAMPLING(S); ①選出與B中相對應的矩陣的列,構造矩陣C; ②計算矩陣C的左奇異向量UC; ④每個j∈[1,2,…,c]; repeat:1)若j∈S,則pj=0; 步驟3 更新抽樣點的抽樣概率p/‖p‖2; return 概率集合p和采樣后的矩陣C; 算法4 通過QR分解的Nystr?m。 輸入:采樣后的矩陣C,核函數f,目標秩k; 1) 對矩陣C執行QR分解:C=QR; 2) 計算特征值分解:RW+RT=V′Σ′V′T; 3) (16) 特征點Z∈p×c的整個估計核矩陣的k個主要的特征值和特征向量的時間復雜度為O(pnc+nc2+nck),其中O(pnc)表示組成矩陣C和W的時間復雜度,而QR分解的時間復雜度是O(nc2),計算RW+RT的時間復雜度是O(n3),計算矩陣乘法的時間復雜度則是O(nck)。 舉個簡單的例子,如核矩陣是一個3×3的矩陣: 假設對核矩陣進行均勻采樣,采樣的列為c=2,假設采樣的列為第1列和第3列,即: 在標準的Nystr?m方法中,首先要計算的是內部矩陣W的最佳近似。根據標準的Nystr?m方法的計算公式,可以得到: 可以計算矩陣C的QR分解,即C=QR 計算RW+RT并得到其特征值和特征向量,即RW+RT=V′Σ′V′T: 對于相同的秩,Nystr?m與QR分解相結合得到的最佳近似矩陣的精度較高。 本文采用的是改進的Nystr?m方法,即對Nystr?m中的矩陣C進行QR分解,得到矩陣Q和R,然后利用得到的R以及Nystr?m方法中的內部矩陣W+,得到矩陣RW+RT,并對其進行奇異值分解,利用矩陣V′、Σ′和V′T3個矩陣,最后根據式(13)得到最佳的Nystr?m近似。這樣做的好處是: 1)算法的時間復雜度降低。首先將觀眾對電影的評分矩陣運用馬氏距離轉化為觀眾與觀眾或者電影與電影之間的相似度矩陣,然后利用Nystr?m方法的特性,即Nystr?m的對象是對稱的半正定矩陣,對相似度矩陣B進行自適應采樣,相對于原始的觀眾對電影的評分矩陣來說,從規模上大大地減小了,因此,該方法從計算效率上來說,有了較明顯的改善。 2)算法的空間復雜度降低。本文是對矩陣B進行了自適應采樣,由于Nystr?m方法的特性,只需要對其中的列進行采樣即可,相對于CUR中需要同時采樣數據的行和列,本文所提出的算法的計算復雜度降低了,同時也將原始的高維數據降低到一個低維的子空間中,因此,在一定程度上也解決了大規模矩陣溢出的問題。 3)精度提高。相對于標準的Nystr?m方法,改進后的算法對矩陣C進行了QR分解,利用矩陣R以及矩陣W的偽逆,得到一個新的矩陣RW+RT,并對其進行SVD,相對于直接對觀眾對電影的評分矩陣進行SVD,采樣后的矩陣更能表示觀眾或電影的特征,因此,經過改進的Nystr?m方法的精度有了較大的提高。 定理1 算法的時間復雜度。算法時間復雜度為:O(nc2),其中k為矩陣的秩,c表示的是采樣的列數,n表示原始大矩陣的規模。 證明 改進后的Nystr?m方法與QR相結合的時間消耗主要有幾個方面:第一個是自適應采樣的時間復雜度O(nc2+Mc),其中,M表示相似矩陣B的中非零點的數目,k為矩陣的秩,c則表示的是采樣的列。另一個是形成矩陣W和C的時間復雜度O(nc2),RW+RT特征值分解的時間復雜度為O(c3),QR分解的時間復雜度為O(nc2),核矩陣的k個主要的特征值和特征向量的時間復雜度為O(pnc+nc2+nck),最后是計算矩陣QV′的時間復雜度O(nck),但是由于n?c>k,因此,總的時間復雜度為O(nc2)。 本文采用真實的觀眾對電影的評分數據集進行測試,并將本文所提出的算法與已有的偏好特征提取算法(SVD、CUR、標準的Nystr?m方法、Nystr?m+RSVD、EMD-QR)進行對比。 本文中的所有實驗都是在一臺8 GB DDR3內存和主頻為2.8 GHz的Intel Pentium CPU的計算機上進行的,計算機的系統為Windows7 64 b,所有的實驗所用的軟件為Matlab 7.0。由于實驗中可能存在一些不確定因素,因此,每次實驗都做了6次,取其平均值作為最后的結果。 該實驗中所采用的數據集是由著名的電影公司Netflix提供的數據集,該數據集中共包括480 189個用戶,17 770部電影總計100 480 507條評分記錄。觀眾對電影的評分的有限性,導致數據集的稀疏性,且觀眾的類型也相對較多,對不同電影的評分也各不相同,導致該數據集的規模相對較大,對該數據集進行分析,運用傳統的特征提取方法效率較低,運用本文提出的改進的Nystr?m方法,對其進行偏好特征的提取。 為了說明本文提出的改進的Nystr?m方法的優勢,將其與已有的算法進行了比較。 1)CUR:CUR也是一種提取偏好特征的方法,但是相對于Nystr?m方法來說,需要對矩陣的行和列采樣得到矩陣C,計算的復雜性會較高。由于Nystr?m方法的特殊性,只需要對矩陣的行或列采樣即可得到矩陣C,因此,相對來說,計算的復雜度也會相應降低,占用的空間相對較小。 2)SVD:SVD是一種普遍的矩陣分解技術,對于特征提取來說,SVD是一種有效的方法,它能夠將高維的數據降低到一個低維的子空間中,從而能降低對矩陣分析的復雜性,但是對于觀眾對電影評分這樣的高維稀疏矩陣來說,并不推薦SVD。 3)標準的Nystr?m方法:由于受到內部矩陣秩的影響,導致整體的秩會受到限制。改進的Nystr?m方法是在標準的Nystr?m方法上作了修改,在標準的Nystr?m方法上將矩陣的內部矩陣進行QR分解,利用分解后的矩陣重新構造最佳的Nystr?m近似。 4)Nystr?m+RSVD:RSVD是SVD的一種推廣。在求解稀疏SVD的過程中需要進行多次迭代,因此,算法的時間復雜度相對較高,與Nystr?m相結合后,雖然能夠降低矩陣分解的復雜性,但是對于大規模的矩陣來說,并不推薦此方法。 5)EMD-QR:EMD算法首先要計算一個有代表性的數據子空間和一個近乎最優的降序排序近似,然后通過獲得集群質心和指標進行矩陣分解。EMD-QR在采樣時需要選擇行和列,因此,對于大規模的矩陣來說,計算的時間復雜度也會有所增加。 本文中首先將用戶對電影的評分矩陣轉化用戶與用戶的相似度矩陣,用自適應采樣方法得到C,然后對矩陣C進行QR分解,得到Q和R兩個矩陣,然后利用矩陣R和W重新構造矩陣,并對構造后的矩陣進行SVD分解,得到V′、Σ′和V′T3個矩陣,然后利用得到的矩陣Q、V′和Σ′重新構造最佳的Nystr?m近似。矩陣恢復的能力越好,則說明該方法的精度越好。 從表1中可以看出,在同等條件下,即電影特征數量相同的條件下,可以看出與CUR、SVD、Nystr?m+RSVD、Nystr?m+EMD-QR以及標準的Nystr?m方法相比較,本文提出的與QR分解相結合的Nystr?m方法的近似誤差更小,所用時間也較小。RSVD算法中,需要進行多次迭代,時間復雜度會較高[25]。EMD-QR算法中需要對行和列進行采樣[26]。本文提出的方法是在標準Nystr?m方法的基礎上進行的改進,與標準Nystr?m方法不同的是,該方法是將Nystr?m方法的內部矩陣C進行QR分解,得到Q和R兩個矩陣,然后將矩陣R和標準Nystr?m方法中的矩陣W+相結合,得到重新組合后的矩陣RW+RT,并對其進行分解。因此,與標準的Nystr?m方法相比較,得到最佳近似矩陣,矩陣的規模相對較少,用到的時間就會相應減少,采樣用到的方法是自適應采樣方法,因此近似誤差也會相應地減小。與CUR方法相比較,CUR中的采樣方法用到的是統計影響力的方法,但是需要對矩陣的行和列同時進行采樣,與Nystr?m方法的只需要對矩陣的列進行采樣而言,用到的時間也會相應減少。對于SVD,直接對原始的觀眾對電影的評分矩陣進行SVD,由于原始的觀眾對電影的評分矩陣較為稀疏,得到的偏好特征的誤差也會較大,且由于原始矩陣規模較大,因此,用到的時間也會有所增加。Nystr?m+RSVD方法由于受到矩陣規模的影響,時間復雜度會較大,而Nystr?m+EMD-QR方法需要對行和列進行采集,因此,對于大規模的矩陣也不推薦此方法。 表2中描述的是在不同的數據集上不同算法的精度,對于采取不同比例的樣本,各種方法上的精度各不相同。DCKFCM算法是在KFCM算法的基礎上進行的改進,k-means算法對于非凸數據集很實用[27],但是對于非凸的數據集,如表2中的數據集,就不能采用k-means算法,因此,對其進行了改進,得到DCKFCM算法。CURE算法雖然對傳統的方法進行了改進,但是由于這種方法采用的是隨機抽樣算法,因此,采樣的精度并不會很高,也會影響最后的結果。表2中的數據是非凸數據集,有些算法對數據有要求,即只針對凸數據集,因此本文中用非凸數據集進行了比較。綜合表1和表2,本文中提出的算法既適用于凸數據集,同樣也適用于非凸數據集。 圖1中描述的是標志點數目對不同方法的近似誤差的影響,可以看出,標志點的數目越多時,近似誤差也會隨之減小。由于采樣后矩陣的規模會相應減小,當采樣的數目較少時,可能會失去原有矩陣的特性,導致近似誤差較高,因為觀眾對電影評分的稀疏性,當標志點的數目較少時,可能會出現偶然性,但是對著標志點數目的增加,采樣后的矩陣與原始矩陣的差距會進一步減小,因此,隨著標志點數目的增加,近似誤差也會相應地減小。影響觀眾對電影評分的因素有很多,但是只有前k個特征對其影響較大,基本上可以代表用戶的特性,因此,當標志點的數目繼續增加時,對其近似誤差的影響也很小。 表1 各種方法的近似誤差和運行時間 表2 不同算法在不同數據集不同比例樣本時的精度對比 圖1 各種算法與通過QR分解的Nystr?m方法的比較 圖2表示的是各個標志點中不同方法的時間比較圖,當選取的標志點的數目增加時,所用的時間也會增加。在一定范圍內,隨著標志點數目的增加,精度也會隨之提高,但是由于采樣方法的不同,獲取相同數目的標志點所用的時間也不同:CUR中用到的是基于統計影響力的采樣,需要對矩陣的行和列同時進行采樣,與Nystr?m只需要對其中的行和列進行采樣相比,時間自然會增加;SVD是直接對原始矩陣進行分解,因此,所用的時間最多;EMD-QR與Nystr?m相結合,雖然在一定程度上時間會相應的減少,但是EMD-QR也需要對行和列進行采樣,因此,所用的時間也比本文提出的方法多。 圖2 各種算法的時間比較 圖3表示的則是各種Nystr?m方法和本文中提出的與QR相結合的Nystr?m方法,當選取的標志點的數目相同時,各方法的精度也會有所不同,這是因為不同方法得到的標志點的過程不同,得到的標志點的代表性也會有所差異,當得到的標志點具有普遍代表性時,精度就會高。標準Nystr?m雖然提供了一種求解近似的方法,但是由于受到內部矩陣的局限性,使其得到的最佳k秩近似不具有普遍性,只能得到與特定標志點選取的方法相結合,但是改進后的Nystr?m方法可以與任意標志點選取的方法相結合,本文采用的自適應采樣方法,即每次采樣后都要對概率進行重新排布,可以有效地提高采樣的精度,得到的標志點普遍性更高,精確度更高。 從圖4中可以看出,當電影的特征數目相同時,相對于其他方法,本文提出的通過QR分解的Nystr?m方法的近似誤差較小,且隨著所提取的電影數量的增加,近似誤差會越來越小。本文的目的就是對電影的偏好特征進行提取,因此,在影響觀眾對電影評分的前k個主要特征中,所提取的電影的特征越多,近似誤差就會越小。傳統的CUR方法采用的是基于統計影響力的采樣方法,即每一列所占的比重大小,雖然經過采樣后,矩陣的規模會較少,計算的時間復雜度也會相應減小,但是采樣方法的局限性,使得采樣后的矩陣不能保證其原始用戶的特征,即若某列中用戶看過的電影數量較少,但每次的評分卻較高,亦或是觀眾只對其中的某一類電影感興趣,對其評分就會普遍偏高,以及某列中雖然觀眾看過的電影的數量相對較多,但每次的評分卻相對較小,采用統計影響力的結果是前者被選擇的概率可能會大于后者,顯然,這對于分析電影的特征是不利的,前者觀眾可能關注的是某一類電影,而后者看的可能是多類型的電影,而這些電影卻不是用戶真正感興趣的。而SVD中,則是直接對觀眾對電影的評分矩陣進行分解,得到的雖然是電影的特征,但由于原始矩陣的規模較大,這種方法也顯然并不是最佳選擇。標準的Nystr?m方法中,由于針對的是內部矩陣W+,要尋求其最佳k秩近似,因此就對矩陣進行了限制。將Nystr?m與RSVD相結合,雖然采樣后的矩陣規模減小了,但是由于矩陣的稀疏性以及觀眾對電影評分帶有主觀性的特點,影響了該方法的使用。EMD-QR方法是針對低秩矩陣而言的,從中受到啟發,Nystr?m采樣的矩陣即為低秩矩陣,將Nystr?m與QR方法相結合,不僅能從時間復雜度上進行改進,精度也不會受到損害。 圖3 各種Nystr?m方法的精度的比較 圖4 不同電影特征下的近似誤差 本文中描述了基于Nystr?m方法的偏好特征的提取,與傳統的Nystr?m方法不同,本文在標準的Nystr?m方法上作了進一步的改進,不再受內部矩陣的限制,使得Nystr?m方法能與任意標志點選擇方法相結合來尋求最佳k近似。這一點對于規模較大的稀疏矩陣來說尤為重要,選取一定的標志點能夠減小矩陣的規模,本文中采用的是自適應的Nystr?m方法,在算法3中描述了該方法,與傳統的采樣方法相比較,該方法的精度要高于傳統的方法。算法4中進一步說明了經過QR分解的Nystr?m近似,進一步得到其特征的特征向量。用Nystr?m近似后能盡可能保留近似前的矩陣的特性,因此對于精度和效率都有一定的改進。 未來工作包括:1)根據得到的用戶和電影的特征,對用戶感興趣的電影進行推薦。2)本文中主要是對電影數據集進行的測試,在未來的工作中會對更多的不同的數據集進行測試,進一步驗證特征提取的有效性。1 相關工作
1.1 核矩陣
1.2 奇異值分解
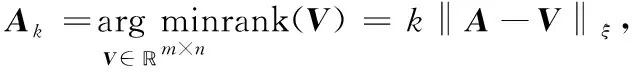
1.3 低秩矩陣近似

1.4 Nystr?m方法
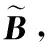
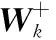
2 自適應Nystr?m方法
2.1 自適應采樣

2.2 自適應Nystr?m采樣
2.3 改進的通過QR分解的Nystr?m方法
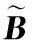
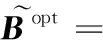
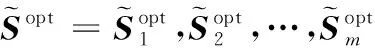
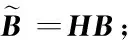
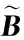
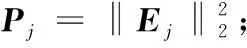

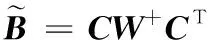
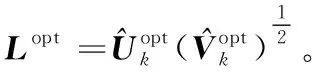
3 算法求解實例



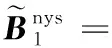


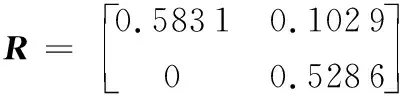


4 算法的評價
4.1 算法的優越性
4.2 算法的時間復雜度分析
5 實驗環境、結果與分析
5.1 實驗環境
5.2 實驗中所用的數據集
5.3 實驗設置
5.4 實驗過程

6 結語

