基于隨機結構的無乘法無限沖激響應數字濾波器設計方法

馮帥棟，陳立家，劉名果

(河南大學 物理與電子學院，河南 開封 475000)

0 引言

數字濾波器是一種信號處理裝置，它能夠降低噪聲、消除干擾，因此被廣泛應用于電視雷達、通信傳輸、生物醫學等各個領域[1-3]。傳統的無限沖激響應(Infinite Impulse Response, IIR)數字濾波器結構中包含乘法器，這影響了濾波器的運算速度，增加了硬件結構的復雜程度[4]。因此，許多學者開始進行無乘法IIR數字濾波器的研究。

在文獻[5-7]中，IIR數字濾波器的無乘法設計是基于經典的濾波器結構(級聯型、并聯型等)將乘法器的系數轉換為二次冪的和或差，然后通過乘法塊進行實現。例如乘法器系數10轉換為乘法塊是23+21，這種二次冪的轉換通常利用CSD(Canonic Signed Digit)碼進行實現，但是通過這種方法設計的無乘法IIR數字濾波器存在系數量化誤差和結構固定的問題，并不能滿足數字濾波器的性能要求。為了優化無乘法IIR數字濾波器的設計方法，一些學者開始嘗試利用演化算法對無乘法IIR數字濾波器進行設計。在文獻[8]中，一種新的無乘法IIR濾波器設計方法被提了出來。該方法首先對加法器的個數進行設定；然后計算出包含相應個數加法器的所有回路，并且以這些回路為種群；最后利用進化的變鄰域搜索(Evolutionary Variable Neighborhood Search, E-VNS)算法對這些回路進行元器件(移位器、延時器、反相器)插入操作，直到元器件的插入對回路的改進沒有效果為止。這種方法雖然在傳統設計基礎上作了改進，但是計算量非常大并且需要大量的元器件去實現，這增加了濾波器結構的復雜度；而且E-VNS算法搜索精度低、耗時長且容易早熟。在文獻[9]中，提出了一種加入成功父代選擇框架的差分進化(Differential Evolution with a Successful-Parent- Selecting Framework, SPS-DE)算法。這種方法將成功的父代個體存儲在一個庫里，當個體進化停滯時，成功的父代個體從庫里被選擇出來替換掉停滯的個體，這樣可以幫助個體逃離不光明的區域以促進種群收斂，有效地平衡了種群探索與開發的能力。鑒于SPS-DE出色的性能，本文將其運用到無乘法IIR數字濾波器設計中。

為了設計一種滿足結構多樣性要求、性能優良的無乘法IIR數字濾波器，本文提出了一種基于隨機結構的無乘法IIR數字濾波器設計方法。本方法利用加入移位器的子系統直接設計無乘法數字濾波器，不存在對乘法器系數的量化，然后通過SPS-DE對結構進行優化，設計的濾波器具有滿足要求的隨機結構，并取得了較好的濾波器性能。最后，本文分別利用SPS-DE、遺傳算法(Genetic Algorithm, GA)[10]、粒子群算法(Particle Swarm Optimization, PSO)[11]、差分進化(Differential Evolution, DE)算法[12]、多精英指導擁有轉移機制的差分進化算法(Adaptive Multiple-Elites-guided Composite Differential Evolution algorithm with a shift mechanism, AMECoDEs)[13]進行了無乘法IIR濾波器設計，對算法的性能進行了分析，然后將本文方法和現有的無乘法濾波器設計方法進行了對比，對本文方案的有效性進行了驗證。

1 無乘法IIR數字濾波器結構的生成

IIR數字濾波器可以通過差分方程表示：

(1)

從式(1)可以看出，數字濾波器由加法器、乘法器和延時器這些基本的元器件構成。在本文中，提出的方法利用移位器設計了一種穩定的二階子系統，通過二階子系統對無乘法IIR濾波器進行設計。二階子系統由4個移位器，2個延時器和3個加法器構成，它的結構如圖1所示。其中a、b、c、d代表4個移位器，z-1表示延時器，3個黑點代表加法器，箭頭代表了信號流向。

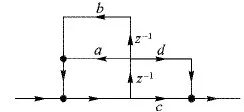
圖1 二階子系統

1.1 生成指令

本文將二階子系統視作基本單元，從濾波器系統的輸入端開始按照生成指令依次添加子系統直到一個完整濾波器結構的形成，生成指令控制著子系統如何被添加到初始的濾波器系統中。

每一個生成指令由4部分構成：指令類型(C)、子系統輸入端編號(I)、子系統輸出端編號(O)、子系統的參數(P)，這4部分的值隨機產生。其中指令類型有四種：連接新活動點(C1)、連接已存在的點(C2)、連接系統的輸入端(C3)、連接系統的輸出端(C4)，每種指令類型的產生概率可以自由設置。系統的輸入端被定義為第一個活動點，依照指令類型，子系統的輸入端和輸出端被分別連接到相應編號的節點。執行C1和C4指令時，子系統的輸入端被連接到當前的活動點，輸出端相應的被分別連接到新的活動點和系統的輸出端。執行C2和 C3指令時，子系統的輸入端相應的被分別連接到已存在的點和系統的輸入端，而輸出端被連接到當前的活動點。C1指令執行后，活動點改變，新活動點的編號為先前的活動點編號加1；C2，C3和C4指令執行后，活動點不變。生成指令如圖2所示。

圖2 生成指令格式

Fig. 2 Generation instruction format

1.2 指令序列

所有的生成指令按其產生順序依次連接，就形成了一個指令序列，每一個指令序列代表了一個無乘法IIR數字濾波器的結構。表1給出了一個指令序列的示例。

表1 指令序列

從表1可以看出，這個指令序列由5個生成指令組成。其中表格第1列的ID代表生成指令的序號；表格的第5列代表了子系統中4個移位器的參數值，數字與字母的組合代表一個移位器，如：+L2表示一個正數向左移動2位，-R3表示一個負數向右移動3位；表格的第6列表示子系統的編號，如：第一條生成指令對應的子系統，其編號為S1。

對應表1中指令序列的無乘法數字濾波器結構被顯示在圖3中。其中x(n)和y(n)分別代表無乘法濾波器的輸入端和輸出端，它們被分別編號為1和0；箭頭代表信號的流向；節點3有一個輸出和多個輸入，它代表一個加法器。這個無乘法數字濾波器由5個子系統構成，共包含了20個移位器、10個延時器和16個加法器。

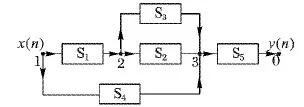
圖3 對應表1的無乘法數字濾波器結構

2 SPS-DE優化無乘法IIR數字濾波器的結構

通過生成指令生成無乘法IIR數字濾波器之后，對代表濾波器結構的指令序列進行編碼，然后利用SPS-DE對它的結構進行優化。濾波器的頻率響應可以通過傳輸函數獲得，適應度通過對設計的數字濾波器的頻率響應與目標頻率響應在采樣點上的均方差的計算來評估。公式如下：

(2)

其中：N為采樣頻率，D(Ki)為設計的濾波器頻率響應，T(Ki) 為目標濾波器的頻率響應。

SPS-DE優化結構的流程如下。

首先對種群進行初始化，每一個個體對應一個指令序列。然后利用適應度函數對個體進行評估，如果滿足目標條件則輸出最佳個體；否則，執行下一步對種群進行變異操作，SPS-DE算法采用差分策略從種群中隨機選出3個不同的個體進行變異操作。然后接著對變異后的種群進行交叉操作，本文采用單點交叉，也就是在兩個不同個體的相同編號節點間進行交叉，實現兩個濾波器之間的結構互換。完成交叉后，對種群進行選擇，其中較好的個體進入下一代繼續進行優化。

因為SPS-DE加入了SPS (Successful-Parent-Selecting)機制，所以種群每一次迭代完成后，就會檢測種群是否停滯。通過計算第g代種群中近來連續未成功進化個體的數目對停滯程度進行評估。公式如下：

(3)

其中：qi(g)、qi(g+1)分別表示第g代和第g+1代種群中近來連續未成功進化個體的數目；Xi(g)代表第g代第i個個體，F(Xi(g))表示其適應度；Ui(g)表示對Xi(g)進行交叉后生成的實驗向量，F(Ui(g))表示其適應度。如果qi(g+1)超過了一個不可接受的值Q，此時種群被定義為停滯。種群停滯時，SPS機制會從存儲成功父代個體的庫里選擇成功的個體對停滯的個體進行替換。成功父代個體p(g)的來源被表示如下：

(4)

其中：Pg代表第g代種群，A代表近來連續成功升級個體的庫，Q代表停滯容忍度。

無乘法IIR濾波器結構優化的具體步驟如下：

步驟1 首先進行種群初始化，隨機產生M個代表無乘法濾波器結構的指令序列編碼，每一個指令序列代表種群中的一個目標向量。

步驟2 對種群中的每個目標向量進行適應度評價，然后判斷是否達到迭代次數。若滿足，則停止計算并輸出最優的個體；否則，執行步驟3。

步驟3 從種群中選擇出不同的個體執行變異操作，生成變異向量。

步驟4 對變異后的種群執行交叉操作產生實驗向量。

步驟5 對目標向量和實驗向量進行適應度評估，從中選擇出最佳的個體進入下一代。

步驟6 判斷種群進化是否出現停滯并且啟動SPS機制，然后返回步驟2。

3 實驗仿真與分析

通過本文的方法設計一個通帶截止頻率為0.4π，阻帶截止頻率為0.6π的低通無乘法IIR數字濾波器，然后利用Matlab進行仿真。在本文中，設計了一些對比實驗對本文方法的有效性進行了驗證。

3.1 移位器位數的對比

為了分析移位器參數范圍的大小對無乘法IIR數字濾波器性能的影響，本文設計了具有不同位數范圍的無乘法IIR濾波器進行對比。移位器的位數被分別設置為5、6、7、8、9、10、11，濾波器的其他設計參數和表2一致，為了平衡4種連接方式的概率，其中C1、C2、C3、C4的概率被設置為等概率。然后分別在每種情況下進行100組測試，將每種情況下最好的實驗結果進行了對比。

如圖4所示，這些無乘法IIR濾波器的通帶波紋都在2.7 dB以內。在過渡帶區域，5位無乘法濾波器的幅頻響應有最快的衰減，在0.6π時已衰減至-64 dB，而6位、7位、8位、9位、10位、11位的無乘法濾波器在0.6π時分別衰減到-58 dB、-45 dB、 -47 dB、-40 dB、-30 dB 和 -36 dB。在阻帶區域，5位～11位的無乘法濾波器的阻帶最大衰減分別為-64 dB， -58 dB， -45 dB， -47 dB， -40 dB， -30 dB 和-36 dB。整體來看，當移位器的位數較小時，無乘法IIR濾波器有較好的性能，這是因為當位數較小時，量化誤差也相對較小。

圖4 不同位數的無乘法IIR濾波器的幅頻響應

3.2 不同算法設計無乘法IIR濾波器的對比

為了分析不同算法對無乘法IIR數字濾波器結構優化的效果，本文分別利用SPS-DE、AMECoDEs、DE、GA 和 PSO設計了一個5位的無乘法IIR濾波器進行對比，濾波器的其他設計參數和表2一致。為了對比的合理性，每種算法的種群數目都設置為100，迭代次數設置為10 000代，算法的其他參數都是在其算法性能最優的情況下進行設置，這5種算法的仿真參數如表3所示，其中：“—”表示沒有參數值。然后在每種算法下分別進行了100組實驗，對每種算法設計的最優結果進行對比。

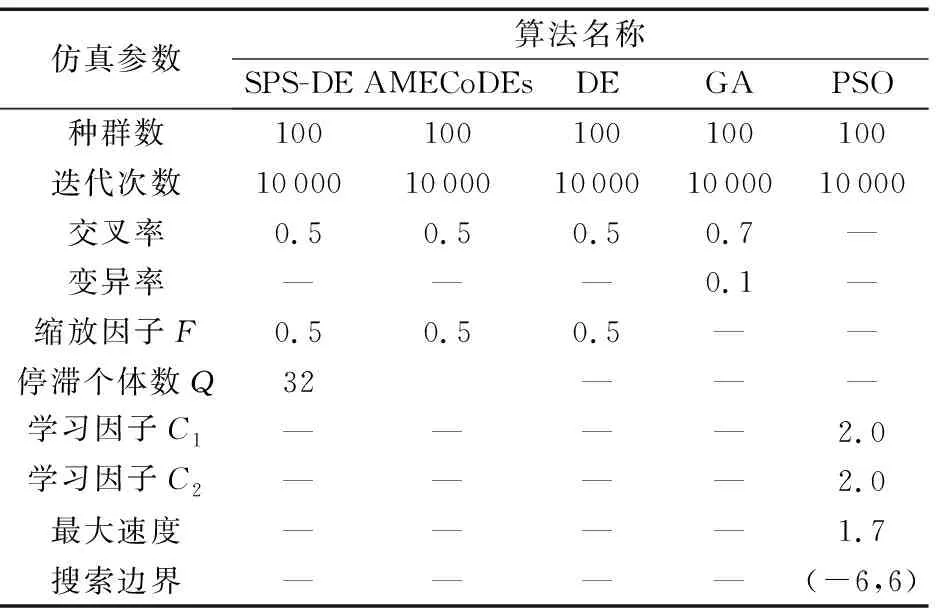
表3 不同算法的仿真參數

正如圖5所示，利用這幾種算法設計的無乘法IIR濾波器的通帶波紋都在2.7dB以內。在過渡帶區域，通過SPS-DE、AMECoDEs、DE、GA和PSO設計的濾波器幅頻響應在0.6π時分別衰減至-64 dB、-49 dB、-50 dB、-35 dB和-45 dB。這些濾波器的阻帶最大衰減分別為-64 dB、-49 dB、-50 dB、-35 dB和-45 dB。

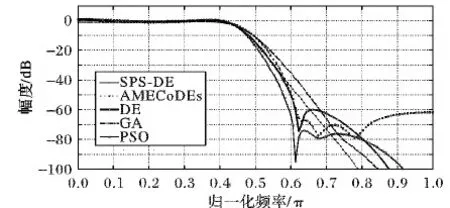
圖5 不同算法設計的無乘法IIR濾波器的幅頻響應

圖6表示每種算法在其算法參數設置最佳情況下的演化曲線，其中SPS-DE收斂最快并最終達到了一個最小值，結果表明利用SPS-DE設計的無乘法IIR濾波器的性能最好。原因是SPS-DE算法加入了成功父代選擇框架，有效地平衡了種群的開發和探索能力，避免了種群陷入局部最優，過早收斂。

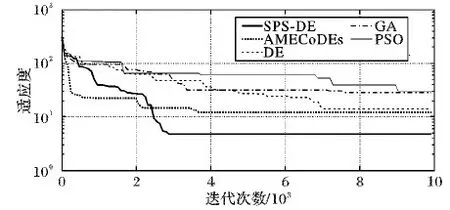
圖6 每種算法的演化曲線

3.3 與無乘法FIR數字濾波器的對比

圖7是通過等波紋法、最小二乘法、最小P次歸一法分別設計的一個通帶截止頻率為0.4π，阻帶截止頻率為0.6π的14階無乘法有限沖激響應(Finite Impulse Response，FIR)數字濾波器，本文設計了一個同樣目標的無乘法IIR數字濾波器與之進行對比，濾波器的設計參數和SPS-DE算法參數如表2和表3所示。如圖7所示，無乘法FIR濾波器和本文設計的無乘法IIR數字濾波器通帶波紋都在1.2 dB以內。在阻帶區域，等波紋法、最小二乘法、最小P次歸一法設計的無乘法FIR濾波器的阻帶最大衰減分別為-32.5 dB，-24.47 dB，-36.7 dB，本文設計的無乘法IIR數字濾波器的阻帶最大衰減為-64 dB。通過數據分析可以看出，本文設計的無乘法IIR數字濾波器性能好于無乘法FIR數字濾波器，這是因為FIR濾波器結構中沒有反饋回路，而IIR結構中含有反饋回路，其幅頻精度較高。因此，在同等條件下，無乘法IIR濾波器性能較好。

3.4 與結構設計無乘法IIR濾波器方法的對比

文獻[8]設計了一個通帶截止頻率為0.7π，阻帶截止頻率為0.906 9π，阻帶最大衰減為-50 dB的無乘法IIR濾波器，濾波器由20個延時器、40個移位器、11個加法器和20個反相器構成。本文設計了一個相同目標的IIR濾波器與文獻[8]進行對比，移位器位數設置為5，其他的濾波器設計參數和表2一致。利用本文方法設計的無乘法IIR濾波器包含了14個延時器、28個移位器、21個加法器和11個反相器，元器件總數目比文獻[8]少了17個。圖8和圖9分別表示文獻[8]設計的無乘法IIR濾波器和本文設計的無乘法IIR濾波器的幅頻響應。文獻[8]設計的無乘法濾波器和本文設計的無乘法濾波器的幅頻響應通帶波紋分別為2 dB和 1.14 dB。在過渡帶區域，本文設計的濾波器幅頻響應在0.9π時已經下降到了-70.2 dB，而文獻[8]設計的濾波器幅頻響應僅下降到-50 dB。文獻[8]設計的濾波器和本文設計的濾波器幅頻響應的阻帶最大衰減分別為-50 dB和 -70.2 dB。通過以上數據分析來看，在通帶截止頻率和阻帶截止頻率相同的情況下，本文方法設計的無乘法IIR數字濾波器通帶波紋減小了43%，阻帶最大衰減下降了40.4%，而且該方法使用較少個數的元器件實現了優良的濾波器性能，這降低了濾波器結構的復雜度，實驗進一步表明了本文方法的有效性。

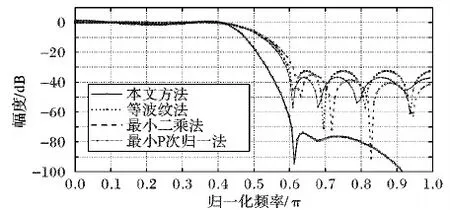
圖7 與無乘法FIR數字濾波器的對比

圖8 文獻[8]中設計的無乘法IIR數字濾波器的幅頻響應

圖9 本文方法設計的無乘法IIR數字濾波器的幅頻響應

4 結語

本文提出了一種基于隨機結構的無乘法IIR數字濾波器設計方法。此方法首先從結構上進行無乘法IIR數字濾波器的設計，然后通過SPS-DE算法對結構進行優化，最后設計實驗進行了有效性的驗證。利用該方法設計的無乘法IIR數字濾波器能夠滿足結構要求，性能得到了提升。這種方法為無乘法IIR數字濾波器的設計拓展了一種新的思路。