基于滑動窗口和ARMA的Argo剖面數據異常檢測算法

羅一迪，蔣 華，王慧嬌，王 鑫

桂林電子科技大學 計算機與信息安全學院，廣西 桂林 541004

1 引言

Argo是第一個實時的、高分辨率的全球立體海洋觀測網，因其活躍性和規模，可以說是海洋觀測史上的一場革命[1]。自2000年實施以來，所獲得的溫度、鹽度剖面數據量比過去100年收集的總量還多。但是Argo浮標易受到環境的影響，尤其是測量鹽度的傳感器，容易受到生物污染、生物殺傷劑泄露等原因的影響，造成鹽度測量產生誤差。而且由于Argo浮標自身的隨機性和拋棄性，海洋工作者們很難對其傳感器進行校正，也很難確定傳感器產生誤差的原因，所以很有可能出現數，其中V2表示待測數值，V1、V3表示與V2相鄰的上下兩個剖面點數據。若測試鹽度，則當壓強＜500 dbar時，檢測值超過0.9 PSU，或者當壓強≥500 dbar時，檢測值超過0.3 PSU，則待測值據誤差或錯誤。為了進一步服務于科研和其他社會應用，需要對于數據的質量精度有一定的保證，所以Argo剖面數據的異常檢測就顯得尤為重要。

關于Argo剖面數據的異常檢測，有大量的學者做了研究工作。文獻[2]提出了一種利用傳統閾值剔除異常數據的方法，其所要求的剖面計算公式為：檢測值=標記為異常。可以看出，該方法只是針對單一剖面數據進行異常檢測，并且沒有考慮采樣點檢測深度間隔的變化。文獻[3]采用“三倍標準差”與傳統閾值判斷相結合的方法實現對Argo剖面數據的異常檢測，該方法結合了鄰近剖面數據，彌補了傳統閾值判定方法的不足，但是該方法采用的是全局靜態閾值，當閾值設置不合適時可能造成某些異常剖面點的誤判或者漏判。文獻[4]將多年的歷史溫鹽觀測數據（南森站和CTD資料）通過最小二乘法擬合得到某地區的溫鹽關系模型，并利用該模型對Argo剖面數據進行質量控制。但是由于溫鹽數據的非線性的特點，采用最小二乘法無法很好地提取出數據特征，因此獲得的溫鹽關系模型精確度不高，導致異常檢測的可靠性也不高。因此，如何對于Argo剖面數據進行有效的異常檢測，并且保證較高的精確度和可靠性，是一個重要的研究問題。

異常檢測[5]（Anomaly Detection）就是識別出與歷史或者預期模式有顯著差別的過程，異常數據可能由于傳感器采集錯誤或者數據傳輸等原因產生。對于異常檢測，國內外學者已經做了大量的研究。文獻[6]利用滑動窗口劃分畜禽物聯網數據流，并通過支持向量回歸模型實現數據流的異常檢測。文獻[7]將變壓器在線監測數據流通過滑動窗口進行篩選，再使用聚類模型實現了對變壓器狀態的異常檢測。文獻[8]利用滑動窗口和LN預測模型獲取水文數據的預測值，并通過對比觀測值與預測值，實現了對于水文數據的異常檢測。通過文獻[6-8]可知，利用滑動窗口可以全面有效地挖掘出時間序列的異常點，而且具有較高的精度和可靠性。

ARMA是一種典型的、應用最廣的時間序列模型。文獻[9]利用ARMA模型實現估計觀測噪聲方差的目的。文獻[10]通過ARMA模型可以有效地探測到地震電離層出現的異常擾動，并且具有較高的精度。文獻[11]利用最小二乘法與ARMA模型相結合的方法，實現了對于衛星導航定位和航天器跟蹤中重要的極性參數的預測。文獻[12]使用ARMA模型預測在線電視劇的流行度，預測結果準確性高，并且具有較高的參考價值。因此，使用ARMA模型可以有效地實現時間序列預測，并且具有較高的預測精確度，是一種理想的預測模型。

基于上述研究，本文采用滑動窗口（Sliding Window，SW）模型與自回歸移動平均（AutoRegressive Moving Average，ARMA）模型實現對于Argo剖面時間序列的預測，然后利用中心極限定理（Central Limit Theorem，CLT）獲得置信區間，對比待測剖面點的觀測值與置信區間之間的關系，實現剖面數據的異常檢測。

2 Argo剖面數據異常檢測

根據國際Argo計劃的要求，每個浮標的循環測量周期是10天，意味著每10天浮標上浮一次[13]，在其循環周期內，浮標測量0～2 000 m水深范圍內的溫度、鹽度數據。因此，Argo浮標剖面數據是包含溫度、鹽度等屬性的時間序列，可以表示為PN={p1,p2,…,pn}，其中 pi=(oi,ti)，表示ti時刻對應的剖面觀測值是oi(1≤i≤n)。

本文的Argo剖面數據異常檢測算法的基本思想：首先利用滑動窗口劃分剖面時間序列，再建立ARMA預測模型，獲得剖面數據的預測值，然后利用中心極限定理計算置信區間，通過判斷觀測數據是否在置信區間內來判斷待測剖面點pi是否異常。整個算法的具體描述如下：

算法Argo剖面數據異常檢測算法

輸入Argo剖面序列PN，k-近鄰剖面點序列的寬度k，置信度 p。

輸出Argo剖面標記序列

步驟1初始化待測剖面點 pi的k-最近鄰窗口ζi=

步驟2建立ARMA預測模型，輸入ζi作為參數，計算獲得預測值i。

步驟3計算對應的上界和下界

步驟4判定待測剖面點pi是否異常。若，則點 pi為正常點，令 flag=1，跳轉至步驟5；否則點 pi為異常點，令 flag=0，跳轉至步驟6。

步驟5后移一位滑動窗口，用 pi替代ζi={pi-2k,pi-2k+1,…,pi-1}中的 pi-1，獲得新的k-最近鄰窗口 ζi+1。

步驟6后移一位滑動窗口，用 pi替代ζi={pi-2k,pi-2k+1,…,pi-1}中的 pi-1，獲得新的k-最近鄰窗口 ζi+1，并以預測值i替換原有的觀測值 oi，即。

步驟7 若i＜n，則i=i+1，跳至步驟2；否則，對PN的異常檢測結束，輸出

Argo剖面時間序列異常檢測算法的流程圖，如圖1所示。

2.1 滑動窗口及Argo剖面子序列的預測

現有的Argo剖面數據異常檢測算法中，多數是利用固定閾值進行判定，但是剖面數據分布會隨著環境的變化而變化。若采用固定閾值進行異常檢測，當閾值設置過大時，會造成錯判，當閾值設置過小時，會造成漏判，所以閾值的設置直接影響著異常檢測算法的精度和可靠性。因此本文引入滑動窗口模型，利用滑動窗口選擇鄰近的多個剖面點來計算預測值，從而可以確定不同的閾值。此外所有的剖面子序列都有可能存在異常數據，而滑動窗口可以遍歷所有的剖面子序列。為了降低計算復雜度，本文依據k-最近鄰原則（k-Nearest Neighbor，KNN）建立滑動窗口，獲得k-近鄰剖面子序列，其定義如下：

圖1 Argo剖面時間序列異常檢測算法流程圖

定義1（k-近鄰剖面子序列）給定Argo剖面時間序列PN={p1,p2,…,pn}和序列中待測剖面點 pi(i＜n)，pi的k近鄰剖面點序列為一個連續的長度為2k的剖面子序列，可表示為ζi={pi-2k,pi-2k+1,…,pi-1}。

滑動窗口寬度k決定了預測模型的輸入參數量，k越大，計算復雜度會相應的增加。而國際Argo計劃希望獲取到的測量精度分別為海水溫度0.005 C和鹽度0.01（PSU/實用鹽標）[1]，因此，在滿足精度要求的情況下，可以適當調節滑動窗口寬度，從而可以降低算法的計算復雜度。

當通過滑動窗口獲得待測剖面點的k-近鄰剖面點序列后，下一步便是通過剖面子序列獲得待測剖面點的預測值。本文采用可以有效地對時間序列進行預測的自回歸移動平均模型（ARMA）。ARMA模型是針對平穩的時間序列的預測模型，而在實際的海洋環境中，可能由于環境影響或者傳感器信號的擾動，所獲得的Argo剖面數據可能是非平穩的，因此為了保證預測精度，在生成ARMA模型前需要判斷Argo剖面時間子序列進行是否是平穩時間序列。若不符合，需進行差分計算轉換為平穩時間序列，再建立ARMA模型。

本文依據最小二乘法（Least Squares，LS）原理估計模型系數，并依據最小信息準則[14]（Akaike Information Criterion，AIC）確定模型階數。參數選擇通常選用的是AIC量最小的參數。AIC可以表示為：

其中，n為樣本大小，σ2為擬和殘差的平方和。

某個待測剖面點pi的k-近鄰剖面子序列為ζi={pi-2k,pi-2k+1,…,pi-1}，在此為了方便描述，記作SM={p1,p2,…,pm}，(m=2k)，其剖面觀測值序列為OM={o1,o2,…,om}，(1≤i≤m)，則具體建模方法描述如下：

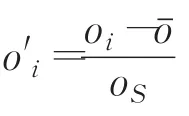
（3）確定剖面預測模型參數的最小二乘估計。對目標函數Q(φ,θ)進行極小化，得到參數的最小二乘估計其中目標函數 Q(φ,θ)表示為：最小二乘估計方法定義如下：

則將目標函數Q(φ,θ)進行改寫得到：

極小化目標函數Q(φ,θ)得到參數的最小二乘估計，依據方程組 (O′,ε′)T[O-(O′,ε′)β]=0 決定，得到解為：

剖面殘差序列的方差的最小二乘估計為：

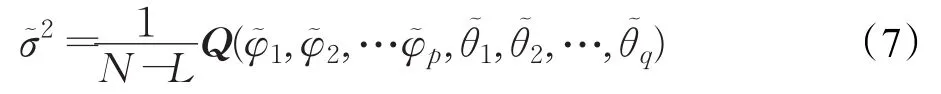
（5）獲得剖面預測值。利用線性最小方差方法獲取剖面預測值，表示為：

及以前的剖面觀測值通過ARMA模型獲得的剖面預測值，φi(i=1,2,…p)為自回歸參數，θj(j=1,2,…q)為移動平均參數，m為經過反標準化過程后獲得的實際剖面預測值。

2.2 異常數據識別與處理

對滑動窗口內的剖面子序列的觀測數據進行預測后，需要利用置信區間（Confidence Interval，CI）來判定下一時刻的剖面點觀測值是否為異常，置信區間是依據中心極限定理（Central Limit Theorem，CLT）來確定的，其計算如下：

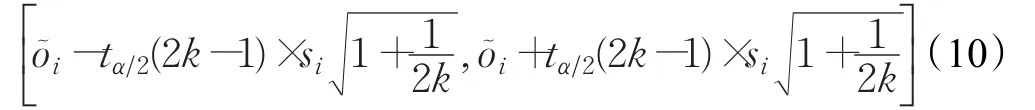
對于給定的Argo剖面時間序列PN，若待測剖面點pi(i＜n)的剖面觀測值oi沒有在閾值范圍內，則待測剖面點 pi被判定為異常剖面點，否則為正常剖面點。為了能夠更好地表示出剖面數據是否異常，用Argo剖面標記序列來進行表示，其定義如下：

定義2（Argo剖面標記序列）完成異常檢測后，對PN中的每一個點增加一個屬性 flag，來標記檢測結果。此時，所獲得的Argo剖面標記序列可表示為，其中，當檢測結果正常，令 flag=1，否則令 flag=0。

當某一待測剖面點 pi經過異常檢測后，需要向后移動滑動窗口進行下一個點的檢測。為了提高檢測的精度，在本文算法采用異常檢測緩解策略[17]（Anomaly Detection and Mitigation Strategy）。

當待測剖面點pi經過檢測后，判定為正常剖面點，則直接后移一位滑動窗口，更新k-最近鄰窗口ζi+1，進行下一個點的檢測；若判定為異常剖面點，更新滑動窗口后，需要使用預測值i替換原有的觀測值oi，獲得新的k-最近鄰窗口ζi+1，再進行下一個點的異常檢測。圖2所示為異常檢測緩解策略示意圖。

圖2 異常檢測緩解策略示意圖

3 實驗結果與分析

為了驗證本文算法的效果，本章從預測精度和異常檢測效果兩個方面對本文所提算法進行實驗驗證，并與同類經典算法進行對比，分析其優劣性。

實驗采用從中國Argo實時資料中心（http：//www.argo.org.cn/）獲取的2016年全球Argo浮標剖面數據進行實驗，實驗數據以.dat文件表示，在Argo剖面文件中包括浮標號、數據采集的經緯度、采集時間等基本信息和壓強、溫度、鹽度屬性信息，少數還包括葉綠素濃度、溶解氧等信息。本文的實驗環境：CPU為Intel Core i3，2.3 GHz，4 GB內存，操作系統為Windows 7，開發工具為MyEclipse2016，編程語言為Java。

3.1 數據預處理

原始的Argo剖面文件中除了包含多個主要的數據屬性外，還包含了大量的與剖面數據異常檢測無關的冗余數據，因此無法直接檢測原始Argo剖面文件，需要對于數據進行預處理，提取出所需要的屬性。而且Argo浮標所觀測到的剖面數據具有明顯的地域性特點，溫度、鹽度等數據的變化在不同的經緯度下呈現不同的變化趨勢[15-16]，因此不能將所有的數據進行統一的處理，需根據經緯度網格進行劃分，再進行數據異常檢測。本文算法將Argo剖面數據按照經緯度網格3°×3°進行劃分，再選取某一網格中的數據進行實驗驗證。

本文實驗采用鹽度屬性進行驗證，如圖3所示，為經緯度為15°N～18°N，138°W～141°W范圍內的鹽度剖面數據曲線，共有2 011個剖面點。從圖3可知，鹽度剖面具有周期性，數據整體平穩，但是也存在一些明顯的可疑點。

圖3 15°N～18°N，138°W～141°W鹽度剖面序列

3.2 預測結果

在本文算法中，預測剖面數據是核心步驟，因此，為了檢測預測效果，本實驗采用均方根誤差（Root Mean Square Error，RMSE）和相對均方根誤差（Relative Root Mean Square Error，RRMSE）來對于預測結果進行量化評估。

文獻[17]中表明LN（Single-Layer Linear Network Predictor，單層線性網絡預測模型）預測模型可以獲得理想的預測效果，因此在表1中對比了在滑動窗口寬度k=8，k=10和k=12的條件下本文預測模型和LN預測模型的鹽度剖面預測誤差。從表1可以看出，本文預測模型的RMSE和RRMSE均小于LN預測模型，在本算法中具有較高的精確度，可獲得更好的預測效果。

表1 不同滑動窗口寬度下鹽度剖面預測誤差

表2所示的是本文預測模型在不同的滑動窗口寬度k下的鹽度剖面預測誤差。從表2可以看出，隨著滑動窗口寬度k的不斷增大，RMSE和RRMSE不斷地減小，因為隨著輸入的預測參數的增加，預測結果會越準確。

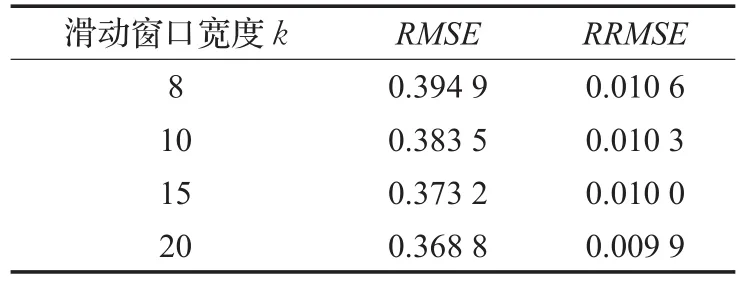
表2 不同滑動窗口寬度的鹽度剖面預測誤差

圖4所示為鹽度剖面序列的預測結果，從圖5可以看出，預測數據大都與原始觀測數據十分接近，只有部分數據與觀測數據有較大的偏差，說明本預測模型的預測精度較高，可以有效地應用于Argo時間序列的異常檢測中。

圖4 鹽度剖面序列的預測結果

3.3 異常檢測結果

從上節可以看出，本文算法采用的預測模型，可以獲得較好地預測結果，因此，在此預測基礎上，可以實現對于鹽度剖面序列的異常檢測。滑動窗口寬度k=10，置信度p=95%條件下的異常檢測結果，如圖5所示。

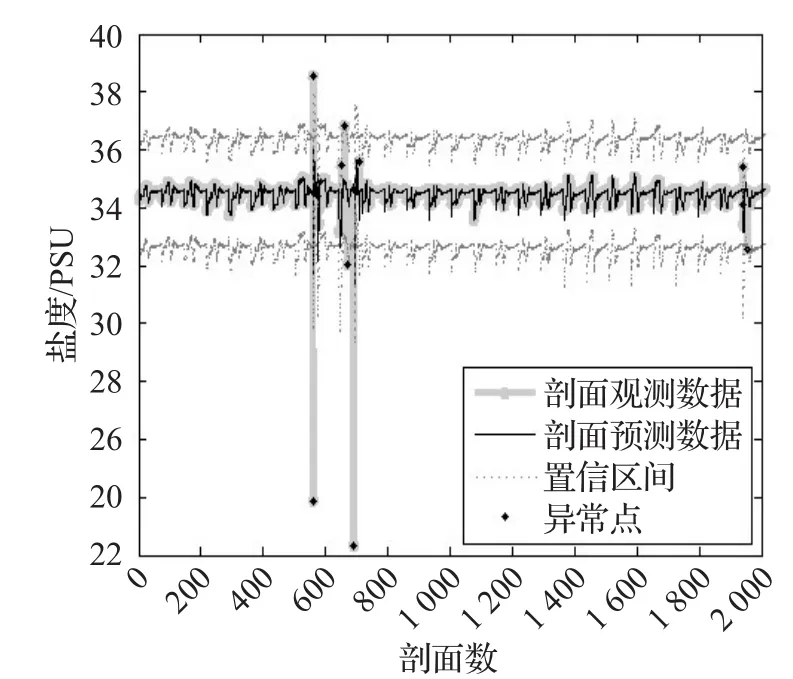
圖5 k=10，p=95%條件下的異常檢測結果

不同的滑動窗口寬度和置信區間下異常檢測的結果可能是不同的。為了能夠有效的評價本算法，在此將異常檢測結果分為4類，如表3所示。其中，TN和TP是希望出現的結果，而FN和FP是判定出現錯誤所出現的結果。

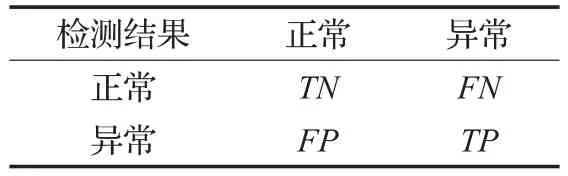
表3 檢測結果分類

不同參數下的異常檢測結果如表4所示。當選擇滑動窗口寬度k=10，置信度 p=95%條件下，本文的異常檢測算法可以正確檢測出異常剖面點10個（TP=10），正常剖面點被正確判定出來的剖面點有1 994個（TN=1 994），但是有2個正常剖面點被錯誤的判定為異常剖面點（FP=2），最后，還有5個異常剖面點沒有被檢測出（FN=5）。

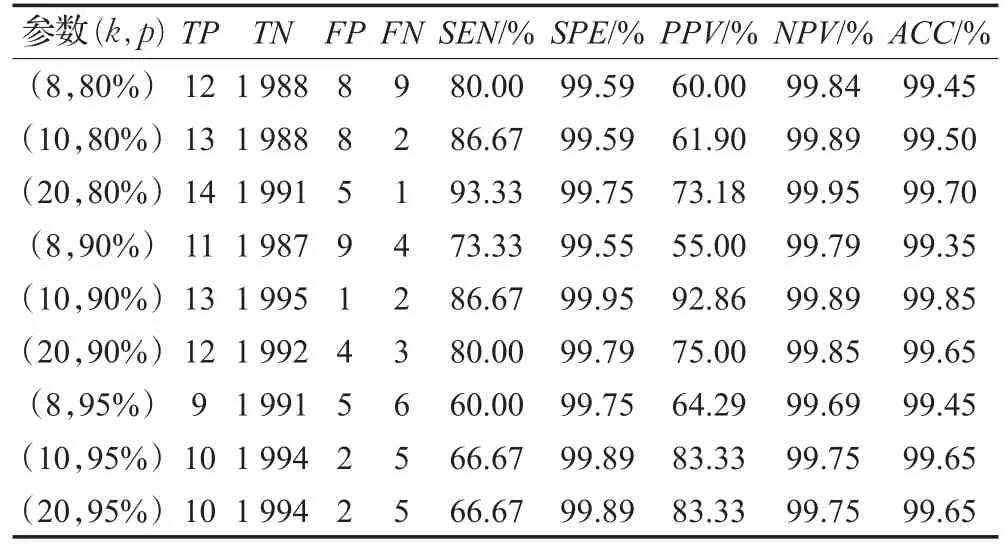
表4 不同參數對異常檢測的結果對比

通過對比表4的評估結果可以看出，本文的異常檢測算法的特異度很高，一直保持在99%以上，說明本算法可以很好地檢測出正常剖面點為正常。但是，當置信度 p≥95%時，敏感度只有60%左右，說明當置信區間范圍設置過大時，能夠真正判斷出異常剖面點的效果不是很好，而當置信度設置在 p∈[80%，90%]范圍內時，敏感度可以維持在80%以上，而且隨著滑動窗口寬度k的增加，敏感度呈上升趨勢。此外，本文算法的精確度一直維持在99%以上，說明本文算法可以準確地判斷出正常剖面點或者異常剖面點，其他的指標也維持較高的水平。當滑動窗口寬度k∈[10,20]，置信度 p∈[80%，90%]時，敏感度可以達到85%以上，并且特異度可以維持在99%，準確度在99%以上，說明本文的異常檢測算法具有較高的可靠性。

為了能夠更好地評估本文的異常檢測算法，將本文方法與其他的異常檢測方法在同一張“受試者工作特征”[18]（Receiver Operating Characteristic，ROC）曲線上。在ROC曲線中，橫坐標是“假正比率”（False Positive Rate，FPR），縱坐標是“真正比率”（True Positive Rate，TPR），兩者的公式為：

在進行算法比較時，當一個算法的ROC曲線被另一個算法的ROC曲線完全“包住”，則可說明后者的性能優于前者。從公式（12）可以看出，FPR就是“1-特異度”，而TPR就是“敏感度”。在異常檢測中，理想的是獲得高TPR，低FPR，意味著曲線越接近坐標軸的左上角，算法的精確度越高，性能越好。

圖6所示的是本文的異常檢測算法與經典的溫鹽關系模型的異常檢測方法[4]、基于“LN”預測模型的異常檢測方法[6]和k-近鄰方法[19]的ROC曲線對比圖。圖6表明，本文方法的異常檢測效果優于其他異常檢測方法。溫鹽關系模型方法采用的是最小二乘法擬合歷史溫鹽數據獲得上下界來實現異常檢測，但是由于該模型的精確度不高導致異常檢測的效果是最不理想的。k-近鄰方法的效果雖然優于溫鹽關系模型方法，但是相較于其他兩種方法，檢測效果一般。基于“LN”預測的方法與本文方法檢測效果較為接近，但是由于該方法的選取的預測模型應用于Argo剖面數據集中，預測誤差較大，所以其檢測效果相較于本文方法略遜一籌。而本文方法的ROC曲線始終位于最上方，完全“包住”了其他3種方法，所以檢測效果最好，準確性高。

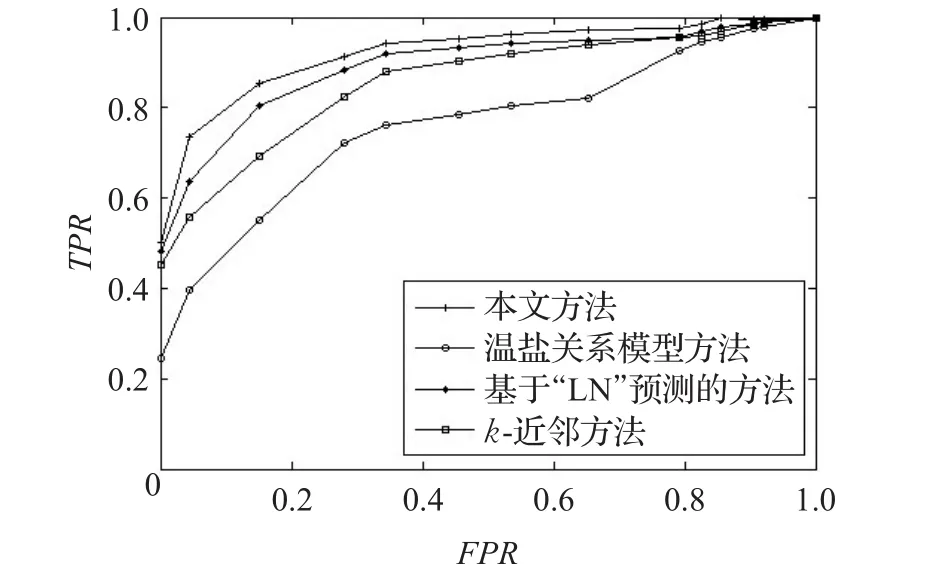
圖6 不同方法的ROC曲線

4 結束語

本文針對Argo剖面數據，提出了一種基于滑動窗口和ARMA的Argo剖面數據異常檢測算法，本文算法利用滑動窗口劃分剖面序列，結合ARMA模型獲取剖面預測數據，并采用中心界限定理計算出動態閾值來實現異常檢測的方法。通過真實的全球Argo浮標剖面數據進行實驗，驗證了本文方法的異常檢測準確性和可靠性高，能夠有效地提高Argo浮標剖面數據的數據質量，具有較高的實用性。在此基礎上，下一步將研究多屬性下對于Argo剖面的異常檢測，為其他領域的研究提供更高質量的Argo剖面數據集。