蛇形管高壓加熱器蒸汽入口區溫度場研究

張馬駿，楊志剛，牛忠華

(上海電氣電站設備有限公司電站輔機廠，上海 200090)

0 概 述

因為新能源機組的占比在逐年上升，火電機組將會承擔更多的調峰任務。高效寬負荷發電技術，將在電力行業受到越來越多的重視，因而也對高壓加熱器提出了適應性需求。蛇形管高壓加熱器憑借其優秀的熱彈性和更快的溫升速率，開始受到了廣泛的關注。對于蛇形管高壓加熱器而言，殼側大部分承壓件的金屬溫度已與殼體內飽和蒸汽的溫度相近，但在蒸汽入口區域，由于過熱蒸汽的溫度明顯高于飽和蒸汽的溫度，所以，在該區域的金屬溫度，也相應高于其他區域的金屬溫度。

在標準GB150.2中規定[1]，碳素鋼和碳錳鋼在高于425℃溫度下長期使用時，應考慮鋼材的石墨化傾向，因此，較高的金屬溫度直接影響了后續設計溫度的設定和材料的選擇。現對蒸汽進口區域的穩態溫度場建立簡化的數學模型，分析蒸汽層間隙寬度的變化對隔熱作用產生的影響，并分析殼體溫度場的分布情況。

1 計算項中符號的定義

計算前，首先定義各計算項中的符號，分別設接管內徑為Di、接管外徑為Do、接管高度為H、接管溫度為t(x)、管內蒸汽溫度為t1、接管底部及筒身內壁的蒸汽溫度為t2、接管下半部分溫度為u1(r,z)、筒身溫度為u2(r,z)、管厚度為δ1、蒸汽層厚度為δ2、筒身厚度為δ3、接管導熱系數為λ、管導熱系數為λ1、蒸汽層導熱系數為λ2、筒身導熱系數為λ3。

2 襯套管結構上的溫度分布

2.1 簡化后的模型

蒸汽進口處的結構和簡化后的模型，如圖1所示。h1為管內壁對流系數，h2為接管底部及筒身內壁對流系數。

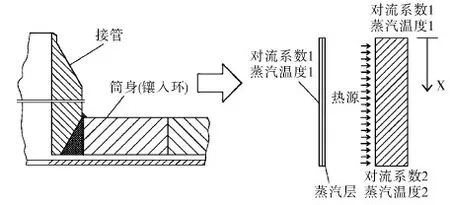
圖1 襯套管結構及簡化后的模型

由于蒸汽的導熱系數比金屬要低很多，蒸汽層能阻擋大部分從過熱蒸汽傳入的熱量，起到了一定的絕熱作用。在接管部分，大部分的熱流會從接管頂部自上而下傳導，少量的熱量通過套管和蒸汽層，從接管內壁面進入接管。因此，可以將其簡化為自上而下的一維熱傳導問題。其中，接管的頂部和底部為一維問題的兩個邊界，均設置為對流邊界。從蒸汽層進入的熱量，可等效為熱源。

使用常物性、帶熱源的一維穩態熱傳導方程[2](x坐標方向自上而下)：

(1)

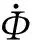
(2)

在式(2)中，等效傳熱系數包括蒸汽對流、套管和蒸汽層三層熱阻。

(3)

邊界條件為：

(4)

(5)

式(3)是二階線性齊次微分方程，通解為θ=C1emx+C2e-mx。利用邊界條件可求得C1和C2，得到最終解：

(6)

2.2 不同蒸汽層厚度下的溫度分布

基于常規的蒸汽進口管的結構數據、熱工及材料數據，選取不同的蒸汽層寬度(0、2.5 mm、5 mm、10 mm、20 mm)。經計算，接管部分的溫度分布，如圖2所示。接管底部位置的溫度隨蒸汽層間隙寬度的變化規律，如圖3所示。

由圖2可知，設置蒸汽層間隙，可有效地降低接管溫度。當蒸汽層的間隙寬度δ2趨于零時，接管部分僅形成10℃的溫降；而δ2增大到2.5 mm時，在接管上產生了50℃的溫降。

圖2 接管的溫度分布(不同的間隙寬度)

圖3 接管底部溫度隨蒸汽層間隙寬度的變化曲線

隨著蒸汽層間隙寬度δ2的增大，接管部分的溫度分布逐漸趨于線性。即蒸汽層間隙寬度δ2越大，從接管內壁面進入接管的熱量越小，蒸汽層間隙的絕熱效果越好。當蒸汽層間隙寬度δ2約為20 mm時，接管溫度幾乎呈線性降低的。

從圖3可知，當蒸汽層間隙寬度較小(<5 mm)時，蒸汽層間隙的隔熱效果對δ2非常敏感，略微增加δ2的寬度，就能大幅度地降低接管溫度。當間隙達到特定寬度后，其隔熱效果已較顯著，繼續增加寬度，不再明顯降低接管溫度。

3 筒身溫度分布

3.1 簡化后的模型

如圖4所示，計算域包括接管底部以及筒身部分。設定接管內壁面為絕熱邊界，接管底部和筒身內壁為對流邊界。接管上下連接位置為第二類邊界條件，同時考慮蒸汽溫度t1和該位置的等效換熱系數he，其余邊界設定為絕熱邊界。

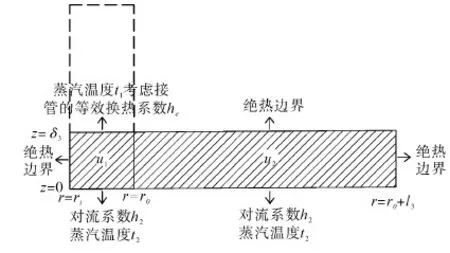
圖4 筒身溫度分析計算域與邊界條件

接管與筒身的溫度場控制方程及邊界條件為：

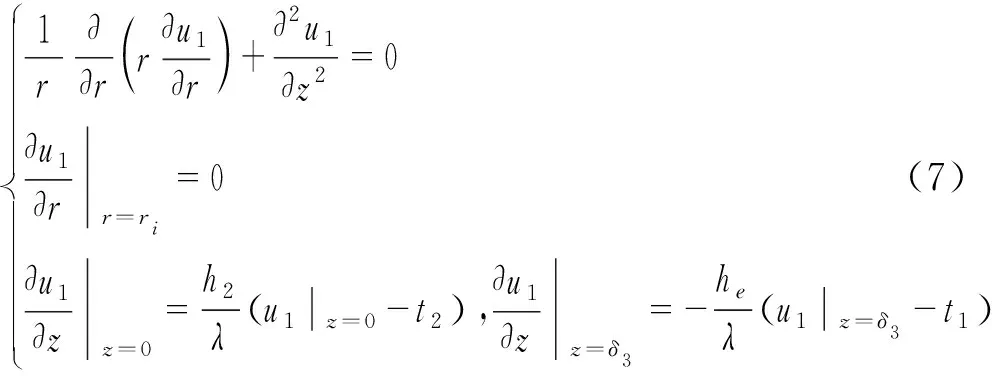
(8)

計算時的銜接條件為：

(9)

3.2 方程求解

式(7)、式(8)均為非齊次邊界條件，無法直接使用分離變量法進行求解。由于方程的解是線性的，因此，可使用疊加原理進行求解。引入u1=v1+w1和u2=v2+w2，其中v1、w1、v2、w2分別滿足齊次方程和邊界[3]。

3.2.1 求解

v1滿足方程：

(10)

使用分離變量法進行求解，令v1=R(r)Z(z)，代入式(10)，分離得到固有值問題：

(11)

和常微分方程：

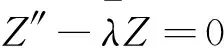
(12)

計算得v1的解為：

(13)

3.2.2 求解w1

w1滿足方程：

使用分離變量法進行求解，令w1=R(r)Z(z)，代入式(14)，分離得到固有值問題：

(15)

和微分方程：

(16)

計算得w1的解為：

[λαncos(αnz)+h2sin(αnz)]

(17)

其中αn為方程(18)的第n個正根。

(18)

在式(17)中：Cn需要利用銜接條件進行求解。

3.2.3 求解v2和w2

同理，可以求出v2和w2，分別為：

v2(r,z)=t2

(19)

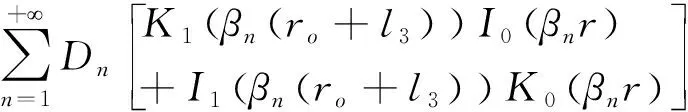
[λ3βncos(βnz)+h2sin(βnz)]

(20)

其中βn為方程(21)的第n個正根。K1,K2,I0,I1分別為第一、二類虛變量Bessel函數。Dn為待定系數，需要利用銜接條件進行求解。

(21)

3.2.4 利用銜接條件得到最終解

w1和w2中仍然有待求常量Cn和Dn，需要利用銜接條件進行求解。

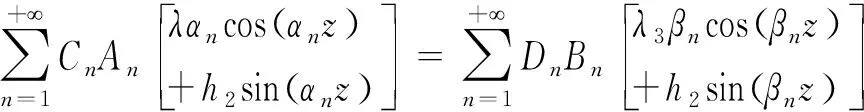
這里為了使表達式更加簡潔，令：

An=K1(αnri)αnI1(αnro)-

I1(αnri)αnK1(αnro)

(23)

Bn=K1(βn(ro+l3))βnI1(βnro)-

I1(βn(ro+l3))βnK1(βnro)

(24)

利用加權余量方法，求解式(22)的系數，權函數為λαncos(αnz)+h2sin(αnz)，則可以得到：

(25)

求得Cn與Dk的關系式：

(26)

這里為了使表達式更加簡潔，令：

(27)

(28)

將式(16)、式(17)、式(19)、式(20)代入式(9)中的(v1+w1)|r=ro=(v2+w2)|r=ro，可得：

(29)

為了使表達式更加簡潔，令：

(30)

(31)

Pn=K1(αnri)I0(αnr)+I1(αnri)K0(αnr)

(32)

Qn=K1(βn(ro+l3))I0(βnr)+

I1(βn(ro+l3))K0(βnr)

(33)

利用加權余量方法，求解式(29)的系數，權函數為λαkcos(αkz)+h2sin(αz)，則可得：

求得Cn與Dk的關系式為：

(35)

聯立式(26)、式(35)，并選取有限項，可得Cn與Dk的線性代數方程組，求解該方程組，并將結果代入式(17)、式(22)，求出v1、w1、v2、w2。利用u1=v1+w1及u2=v2+w2進行計算，可得最終溫度場的分布云圖。

4 算 例

以某工程實例進行試算，計算所得的溫度場云圖，如圖5所示。接管與筒身連接處在z坐標上的溫度分布曲線，如圖6所示。經計算，筒身(鑲入環)連接處的最高溫度,約為446℃，比過熱蒸汽溫度約低54℃，由于該位置溫度仍然大于425℃，所以需設置鑲入環結構。

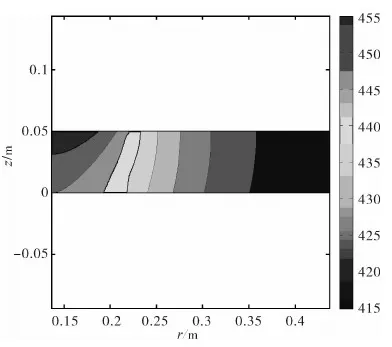
圖5 接管底部與附近筒身的溫度場

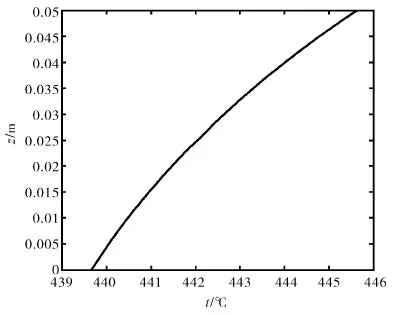
圖6 接管與筒身連接處在z坐標上的溫度分布曲線

5 結 語

建立計算模型后，分析了蒸汽進口區結構對接管隔熱作用的影響，并計算了筒身的溫度場。當蒸汽層的寬度較小時，若改變蒸汽層的大小，對隔熱效果的影響非常顯著；當間隙達特定寬度時，再增加間隙寬度已無法提高隔熱效果。根據計算結果可知，筒身溫度仍然大于425℃，因此，鑲入環結構是設計筒身時必不可少的組成部分。