淺談優化高中數學命題教學的幾點策略

周元

廣西百色高級中學 廣西百色 533000

數學命題是數學教學的重要內容，數學命題涉及的知識廣泛，思維多元，反映了數學的重要規律和思想方法，具有抽象性、符號性、邏輯性等主要特點，對提高學生的數學思維、培養數學語言能力、邏輯思維能力、空間想象能力、運算能力大有益處。本文通過理論思辨和實踐研究相結合，淺談高中數學命題教學的幾點思考。

一、當前高中數學命題教學的現狀

在當前的課堂教學中，數學命題往往是由教師直接給出的，缺少符合學生學情的數學命題生成情境。在數學命題證明的過程中較多的是展示性的講授，習慣性的把課前準備好的證明過程“拋”給學生，輕視對證明思路的探求和數學思想方法的滲透。命題的應用是對所學命題的進一步理解與鞏固，因此學習了命題之后要有相應的習題進行鞏固。很多教師對數學命題習題的選擇具有隨意性，忽視了多種類型的練習題的設計。

二、優化高中數學命題教學的幾點策略

注重創設問題情境

在數學教材中，數學命題大多是用數學語言和數學符號進行描述，但這并不意味著數學命題的教學就必須首先呈現其抽象形式。若設計適宜的數學情境引入，則可吸引學生的注意力，激發學生有意義學習的心向，激活學生數學認知結構中原有的知識，為數學命題的接受或者發現創造有利條件。在教學中，教師應努力創設具有啟發性的問題情境，使抽象的內容具體化，同時也加強數學與生活的聯系，以問題的發現來激發學生的求知欲望，并由此推動學生主動探究。有利用克服傳統數學教學中教師向學生灌輸知識的教學模式的弊端，有利于激發學生的進取精神，有利于培養學生的創新精神和實踐能力。例如，在人教版必修五的《正弦定理》一節中，教師可以先創設問題情境：一艘輪船按照北偏西的方向以28海里/時的速度航行，一個燈塔M原來在輪船的北偏東10度的方向，經過四十分鐘，測得燈塔在輪船的北偏東70度的方向上，求燈塔和輪船原來的距離。接下來教師通過展示問題情境后，引導學生理解題意，畫出圖形，啟發學生發現問題的實質是已知三角形的兩角及其夾邊求其他邊。由此設疑引出課題，使學生一開始就注意到本節課的重要性，從而增強興趣，提高注意力，為突破難點做好思想準備，通過歸結問題的本質后探究三角形的邊角關系。

三、注重特殊與一般的關系

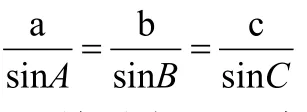
四、注意條件模式的變化

五、注重多元表征的呈現

在數學教學中遵循從生動的直觀到抽象思維再從抽象思維到實踐的認識規律。通過具體直觀教學，使學生形成感性認識，再經過抽象概括上升為理性認識。教具、模型、計算機軟件、投影、電視等都可以用于進行直觀教學，還可以通過讓學生制作一些簡單的教具或模型。例如，一平面截一立方體，截痕可能是幾邊形？當學生的空間想象能力不足時，板圖、教具、電腦動畫等都能夠幫助學生想象、思考。

六、注重命題的靈活應用

數學命題的應用是訓練學生的邏輯能力、發展學生的思維能力的重要途徑。在數學命題的應用前期，要以與命題情境相似的的問題情境中應用數學命題為主，其目的在于使學生鞏固數學命題知識。教學設計中應精心設計多種變式練習，并對練習結果提供及時反饋和糾正。在數學命題應用后期，要以與命題情境不同的問題情境中應用數學命題為主，其目的在于豐富學生的認知，發展學生的數學能力，避免思維定勢，并對數學命題學習的結果進行測量和評價。在定理、公式、法則的應用中，要注意安排好各類例題和習題，既有基本訓練題，又有鞏固知識的題型，還要有綜合型的題目。另外還應適當補充一些逆用、變用定理和公式的題型，以提高學生靈活應用公式的能力。

恰當的命題教學方法能夠有效地激發學生的學習動機，促進學生掌握科學的學習方法，積極主動高效地進行學習。教師在命題教學中應結合教學內容的特點，因“材”確定教學方法和策略，優化教學效果。