分次游遍大慶旅游景區的路線規劃

馬馳 趙光中 高德寶

區域性自駕游越來越受到游客的青睞，如何合理科學地規劃游玩路線，顯得日益重要。本文以大慶的旅游景區為例，采用聚類分析方法對旅游景區進行分組，利用TSP問題模型求解方法規劃每組景區內的行車路線，使得游客既休閑又較優地體驗旅游。

當前，旅游已成為國人的一種休閑時尚和生活常態。但異地旅游總是受經濟條件、交通狀況、旅游時間和景區游玩人員過多等因素的制約，導致游客無法享受旅游。為了更好地享受旅游，全域旅游引起了游客的高度重視。對游客具有最大吸引力的是：全域旅游所追求的，不再停留在旅游人次的增長上，而是旅游質量的提升，追求的是旅游對人們生活品質提升的意義，追求的是旅游在人們新財富革命中的價值。

全域旅游把一個行政區當作一個旅游景區，游客可以自主地規劃旅游方式與旅游路線，基本不會受到旅游團體或導游的約束。為最大程度地享受旅游，旅游路線的規劃是關鍵。旅游線路作為旅游景區的連接主體，其設計的科學合理性和游客需求滿意度直接影響了旅游品質的質量。因此，旅游資源能否變成游客喜愛的產品，很大程度上取決于旅游線路的設計是否成功。本文以大慶市全域內的所有景區為案例，探索分次自駕游遍該市所有景區的路線規劃問題。

一、模型假設及數據來源

（一）模型假設

為了研究和求解方便，本項目對旅游交通線路規劃問題做了一些必要的假設，具體假設內容如下。①游客出行的方式為自駕；②不考慮天氣因素對旅行路線的影響；③旅游線路方案主要影響因素為景點間的駕車時間與距離；④假設游客出游路況良好，交通狀況良好；⑤游客的游玩行為僅限于一個城市區域；⑥高德地圖所提供的路線與相應數據是精確的；⑦游客在旅游景區附近的住宿所需的路程與時間忽略不計。⑧若兩個景區之間的距離小于1千米時，則將兩者合并為一個景區；⑨每個景區的游玩時間不超過6個小時；⑩游客僅在白天的12個小時內駕車與游玩；假設每次旅游的出發點是大慶樞紐站，

編號為s0。

（二）數據來源

大慶現有旅游景區多達50處，其中A級景區0個，“2A”級景區7個，“3A”級景區11個，“4A”級景區12個，“5A”級景區0個，它們分布于大慶的五區四縣（數據來源于大慶市政府網站）。盡大慶兒童公園是“2A”級景區，但它僅適合兒童游玩，所以本文未將其列為研究對象，而選擇了其他所有的“2A”-“4A”級所有景區和相對比較著名的景區油田樂園和紅驥鄉情園為研究對象。事實上，大慶規劃館與博物館均為“4A”級景區，但兩者之間的距離小于1 000米，所以將兩者合為一個景區。同理，將林甸溫泉歡樂谷旅游景區和北國溫泉養生休閑廣場，色氏濕地人家景區和九道溝滿族風情園景區分別合并為一個景區，其編號及名稱如表1所示。因此，本文所要研究的對象共計28個。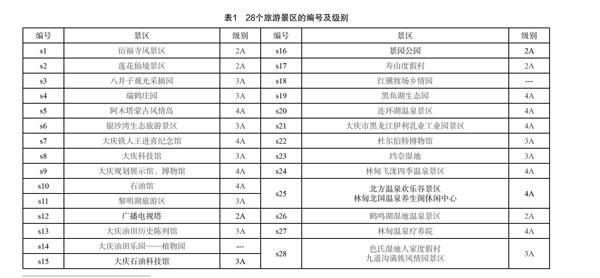

本文所采用的景區之間的路線、距離（單位：千米）與行車時間（單位：分鐘）均來自高德地圖（https：//ditu.amap.com/）的第一個方案，距離和時間采用的是最短駕車距離與其相應的時間。

二、分次游遍旅游景區的路線設計

若游客有足夠的時間，計劃一次游遍所有景區，則是簡單的TSP問題。設n表示景區的個數；dij表示第i（i=1，2，…，n）個景區與第j（j=1，2，…，n）個景區之間的駕車行駛時間；若行車路線經過第i個景區與第j個景區，則令xij=1，否則令xij=0；再令ui為控制子回路變量，則TSP問題的數學模型為：

（1）

由于需要加入出發點大慶樞紐站s0，因此，可假設s0為一個景區，只是沒有賦予其旅游時間，這樣共有29個旅游景區。利用分枝定界法編程求解上面的模型，可得：游遍29個景區時，驅車行駛時間最少應為1 084分鐘，具體的旅游方案如下。

s0（出發，驅車行駛127分鐘）到s2（驅車行駛109分鐘）到s1（驅車行駛98分鐘）到s3（驅車行駛58分鐘）到s4（驅車行駛110分鐘）到s5（驅車行駛12分鐘）到s6（驅車行駛61分鐘）到s20（驅車行駛28分鐘）到s17（驅車行駛21分鐘）到s21（驅車行駛45分鐘）到23s（驅車行駛39分鐘）到s22（驅車行駛47分鐘）到s25（驅車行駛9分鐘）到s24（驅車行駛24分鐘）到s27（驅車行駛35分鐘）到s26（驅車行駛41分鐘）到s28（驅車行駛69分鐘）到s19（驅車行駛38分鐘）到s18（驅車行駛25分鐘）到s16（驅車行駛12分鐘）到s14（驅車行駛7分鐘）到s7（驅車行駛4分鐘）到s15（驅車行駛13分鐘）到s13（驅車行駛11分鐘）到s8（驅車行駛7分鐘）到s10（驅車行駛4分鐘）到s12（驅車行駛17分鐘）到s11（驅車行駛4分鐘）到s9（驅車行駛9分鐘，回）到s0。

多數游客的出行時間總是有限的，本文主要研究的就是尋找每次旅游時間上限，利用較少的次數游遍大慶的所有景區。若要分次游遍所有景區，首先，需要將所有景區分成若干組。然后，根據景區組內景區與景區之間的行車時間規劃行車路線。前者的實現，本文采用的是“就近原則”，按照“聚類分析”的方法對所有景區進行分組；后者需借助于前面所用的TSP問題求解實現。

根據本文的述求：景區組內旅游路線上所需消耗的時間應盡量少，所以，在聚類分析時選擇的是系統聚類。在聚類時，度量標準選擇的是Block距離，它是兩變量值的絕對值之差的和，即

（2）

而聚類方法選擇的是組內平均鏈鎖法，它定義了個案與類之間的組內平均鏈鎖距離。該距離為個案與屬于該類中的每個個案間的距離和類內的每個個案間距離的平均值。

注：根據本文的假設，出發點總是大慶客運樞紐站s0，所以在實際路線中，總是將s0加入到每組景區，所作的規劃路線總是從s0出發，最后返回到s0；由于是休閑旅游，本文所設計的駕車與游玩時間總是很寬松的。

利用SPSS軟件，按照上面的要求對28個景區進行系統聚類，其樹狀圖結果如圖1所示。下面根據圖1中的分組結果進行討論并進行調整。

第一組：s0，s8，s10，s12，s13。利用TSP問題模型求解得（以下幾組求解方法相同，不再敘述）：駕車所用的時間為58分鐘，具體的行車路線如下。

s0（出發，驅車行駛18分鐘）到s10（驅車行駛4分鐘）到s12（驅車行駛11分鐘）到s13（驅車行駛11分鐘）到s8（驅車行駛14分鐘，回）到s0。

根據筆者的實際經驗，這4個景區中任一個景區最多只需3個小時即可游覽完畢，建議游客只需在周六、日兩天時間內完成即可，且還有一些富余時間。

第二組：s0，s9，s11，s19。駕車所用的時間為87鐘，具體行車路線如下。

s0（出發，驅車行駛38分鐘）到s19（驅車行駛36分鐘）到s11（驅車行駛4分鐘）到 s9（驅車行駛9分鐘，回）到s0。

因為s9為兩個“4A”級景區的合并，所以其游玩時間需要接近6個小時；黑魚湖生態景區的溫泉項目均較多，一般需要約5.5小時方能盡興；黎明湖景區約需3個小時。建議游客利用有3天假期的時間休閑游遍三個景區。

第三組：s0，s7，s14，s15，s16，s18。駕車所用時間為126分鐘，具體的行車路線如下。

s0（出發，驅車行駛32分鐘）到s14（驅車行駛10分鐘）

（下轉第頁）

（上接第頁）

到s15（驅車行駛4分鐘）到s7（驅車行駛8分鐘）到s16（驅車行駛25分鐘）到s18（驅車行駛47分鐘，回）到s0。

盡管有5個景區，但每個景區的游玩時間都不會超過4個小時，故需3天時間即可。

第四組：s0，s24，s25，s26，s27，s28。駕車所用時間為262分鐘，具體行車路線如下。

s0（出發，驅車行駛72分鐘）到s24（驅車行駛9分鐘）到s25（驅車行駛20分鐘）到s27（驅車行駛35分鐘）到s26（驅車行駛41分鐘）到s28（驅車行駛85分鐘，回）到s0。

這一組景區里，前4個景區均是以溫泉為主，建議旅游愛好者只選擇一處或兩處即可。基于此，建議游客用兩天時間游玩即可。

第五組：s0，s17，s20，s21，s22，s23。駕車所用時間為285分鐘，具體的行車路線如下。

s0（出發，驅車行駛69分鐘）到s21（驅車行駛45分鐘）到s23（驅車行駛39分鐘）到s22（驅車行駛26分鐘）到s20（驅車行駛28分鐘）到s17（驅車行駛78分鐘，回）到s0。

除s22景區需要2小時左右時間外，其余4個景區均需要5個小時左右。建議游客用4天時間游玩即可。

第六組：不妨將剩下的六處景區合為一組，即：s0，s1，s2，s3，s4，s5，s6。仍用TSP問題模型求解，得驅車所用時間為646分鐘，具體的行車路線如下。

s0（出發，驅車行駛73分鐘）到s3（驅車行駛110分鐘）到s2（驅車行駛109分鐘）到s1（驅車行駛160分鐘）到s6（驅車行駛12分鐘）到s5（驅車行駛110分鐘）到s4（驅車行駛72分鐘，回）到s0。

盡管駕車時間較長，但這6個景區各有特色，需游玩時間不多，所以建議游客用4天左右的時間去游玩。

事實上，游客的每次出發點很有可能不是大慶樞紐站，利用本文的理論方法，只需將大慶客運樞紐站替換為實際出發點，然后重新計算一遍即可。

三、結論

本文針對區域性自駕游問題，采用了聚類分析、0-1整數規劃和分枝定界算法，并且在滿足若干條件下制訂分次游遍大慶全域景區旅游方案。整個方案的制訂過程由淺入深，內容和數據符合實際，保證了方案與實際狀況的貼近程度較高。

（作者單位：黑龍江八一農墾大學）