三角函數最值問題淺談

范登林 西昌市第七中學

研究三角函數的最值問題，其方法與求三角函數值域的方法類似。先通過三角恒等變換，使目標函數變量歸一，函數名稱歸一，然后利用基本函數的值域，求得原函數的最大值與最小值。在實際操作過程中，要注意換元法的應用并注意函數定義域的限制。

求解三角函數最值問題的基本思想：

1、認真觀察函數式，分析其結構特征，確定類型。

2、根據類型，適當地進行三角恒等變形或轉化，這是關鍵的步驟，具體可考慮：①將函數式化成y= Asin(ω x+φ)或y = A s in(ω x + φ ) = f(x)形式，再利用正弦函數的有界性求出最值；②通過換元，將函數解析式化成二次函數、二次方程進行求解，需要注意的是，在換元后，要注意新變元的取值范圍；③轉化為可利用不等式性質，均值不等式來求解的問題；④轉化y為可利用函數的單調性來求解的問題；⑤改變主元，視函數為輔元，從而通過判別式法來分析的最值問題；⑥化歸為可利用幾何解釋來解決的問題。

3、通常可考慮降次，積化和差與和差化積、引入輔助角、萬能代換、換元、配方而對函數式進行變形或轉化。

1、利用輔助角公式

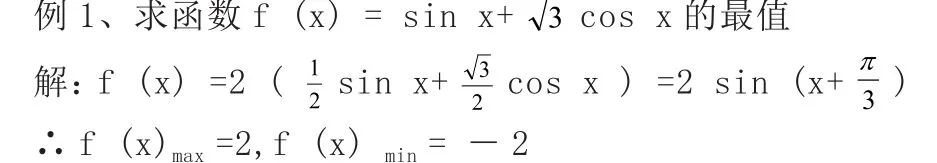
二、利用給定取間二次函數的性質——形如y=at+bt+c二次函數的最值

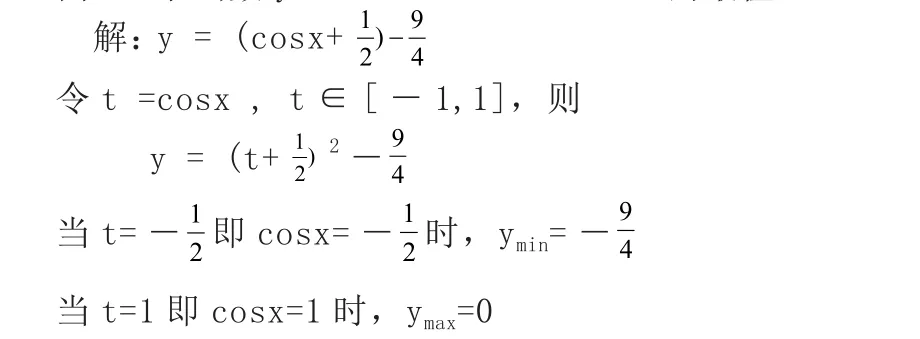
*關鍵：換元、配方，注意新變量的取值范圍例2、求函數y = cosx +cos x－2的最值

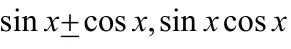
四、利用三角函數的有界性

說明：有些題目可能用以上方法無法解決，或者是可以解決但是很復雜，這時可以考慮運用導數來求解。最好與求導數極值的知識相聯系起來。只不過這里是關于三角函數而已。

注：以上所列舉的方法僅是從一般求解方法上來說的，可能并不適用于所有題目。有些題目比較特殊，無法用以上方法來解，而有些題目用以上很多方法都能解決，這時我們要具體情況具體分析，就要注意選擇簡單恰當的方法來解決。