基于量化依賴Lyapunov函數的有界丟包網絡控制系統的保成本控制

唐曉銘 楊爽 虞繼敏 屈洪春

網絡控制系統(Networked control systems,NCSs)是一種空間分布式系統,其控制回路中的傳感器、控制器、執行器由有限帶寬的通信網絡相連接[1?3].與傳統的控制系統相比,NCSs具有可靠性高、易于維護和擴展、能實現信息資源共享以及遠程控制等優點[4?6].但網絡特有的屬性例如數據丟包、網絡時滯等問題也給控制系統帶來了不可忽視的負面影響.其中數據丟包是造成系統性能惡化甚至破壞系統穩定性的主要因素.很多學者研究了具有丟包的NCS的穩定性分析和控制器設計問題并得到了很有意義的結論[7?12],其中文獻[7]運用隨機丟包模型研究了NCS的H∞控制問題.文獻[8]研究了具有馬爾科夫丟包的量化系統的預測控制綜合問題.文獻[9]研究了具有丟包和多包傳輸的NCS的穩定性問題.文獻[10]研究了有界丟包網絡環境下的多包不確定系統的魯棒預測控制問題.然而文獻[7?10]僅考慮了丟包存在于傳感器與控制器之間即單邊丟包的情況,由于丟包往往同時存在于傳感器與控制器、控制器與執行器之間,即雙邊丟包,因此文獻[7?10]的結果有一定局限性.文獻[11]考慮任意有界丟包過程,解決了具有輸入約束和狀態約束的模型預測控制綜合問題.文獻[12]考慮有界丟包和馬爾科夫丟包兩種情況,分析了系統的狀態反饋鎮定問題.

近年來,由于有限精度算法在數字計算機中的應用,大量學者開始研究量化反饋控制問題[13?22].在眾多研究成果中,主要采用了靜態量化[23?27]和動態量化[28?32]兩種量化方法.由于后者能動態調整量化水平而增加吸引域,因此在處理系統穩定性問題上更具有優勢.然而,由于缺乏統一的研究方法導致其在控制性能問題上仍具有局限性.文獻[23]基于模態依賴的對數量化器,提出了馬爾科夫非線性系統的量化動態輸出反饋控制器設計方法.文獻[24]研究了單輸入單輸出線性時不變系統的量化反饋鎮定問題,證明了對數量化器對于二次型穩定系統的必要性.文獻[25]綜合研究了關于帶有對數量化器的單輸入單輸出系統和多輸入多輸出系統的狀態反饋和輸出反饋鎮定問題,文中量化誤差被處理為區間不確定性,由此將量化反饋控制問題轉化為魯棒控制問題.在文獻[25]的基礎上,文獻[26]提出了量化依賴Lyapunov函數方法,用以處理單輸入和多輸入量化反饋系統的鎮定問題和H∞控制問題.

本文考慮雙邊丟包的情況,給出了單輸入和多輸入兩種情況下的量化反饋網絡系統的保成本控制器設計方法.在分別分析雙邊丟包過程的基礎上,建立了帶有對數量化器的NCS數學模型,進而將具有丟包和量化的NCS的鎮定問題轉化為鎮定一系列系統的魯棒控制問題.基于線性矩陣不等式(Linear matrix inequality,LMI)技術,得到了保成本控制器的設計方法.本文最典型的特點是運用量化依賴Lyapunov函數得到了相較于文獻[25]中二次型Lyapunov函數方法保守性更弱的結果.

注1.本文中,I表示相應維數的單位陣,Rn表示n維歐氏空間(R即R1).對于向量x, u和矩陣,有.在對稱矩陣中,用星號?表示對稱部分.

1 問題闡述

假設被控對象為如下線性離散時不變系統:

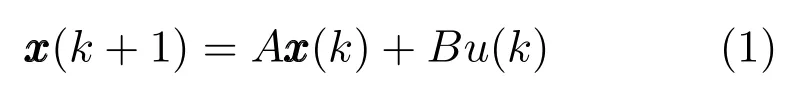
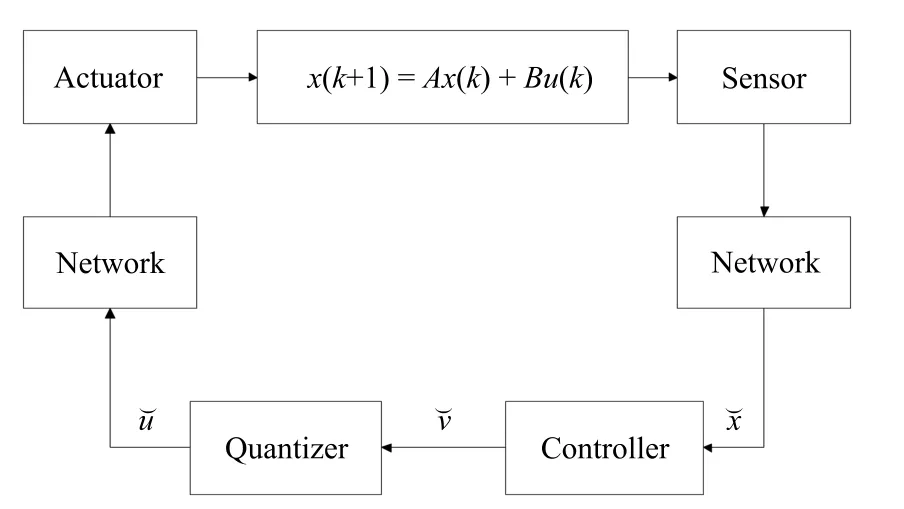
圖1 NCS結構圖Fig.1 The structure of NCS

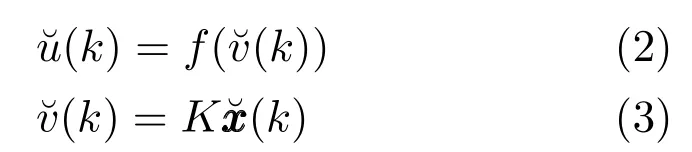
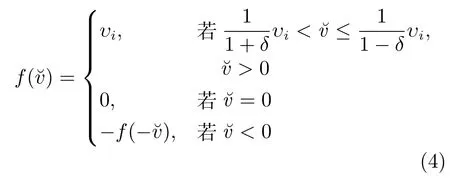
量化水平集為

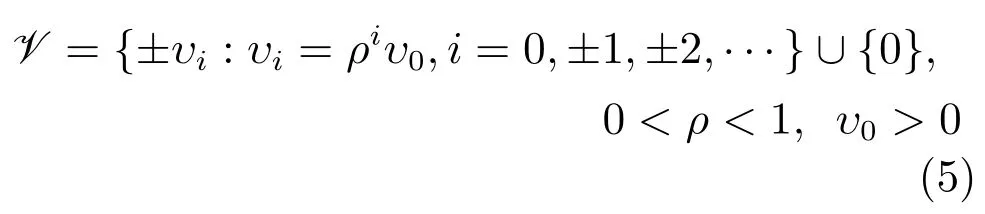
其中,ρ表示量化器密度.δ=(1?ρ)/(1+ρ).假設ρ已知,則δ已知,并且滿足0＜δ＜1.定義量化誤差為

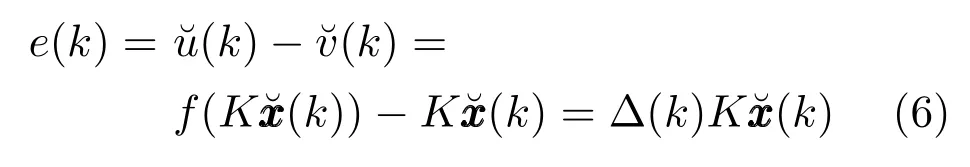
其中,?(k)∈[?δ,δ].

定義1[4].令表示從傳感器到控制器成功傳輸數據的時間點序列,令表示從控制器到執行器成功傳輸數據的時間點序列,都是序列的子序列.令為數據從傳感器到控制器的丟包上界,為數據從控制器到執行器的丟包上界.有界丟包過程定義為,其中,分別從中任意取值.

只有部分成功傳輸的數據能影響閉環系統,因此引入排序因子ord{·}來定義這部分數據.對于任意整數序列,排序因子在不增加或減少任何元素的情況下,對原有整數序列按從小到大的順序進行排序,將得到的序列稱為有序序列.令,其中,對于兩個不相等的正整數a,b,如果出現ia=jb的情況,則在中jb位于ia之前.因此有序序列存在且唯一,使,有序序列σ為實際影響閉環系統的時間序列.

引理1[11].對于定義1中的丟包過程,有μr?,其中,.

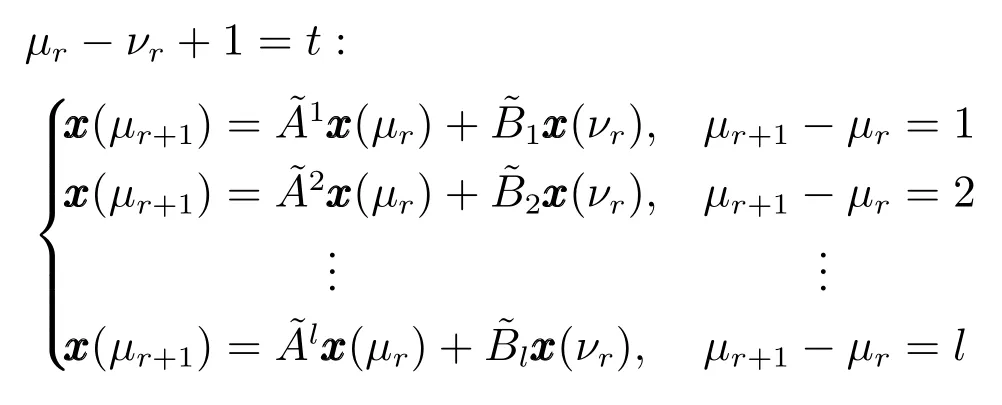
上式可以等價為如下模型:

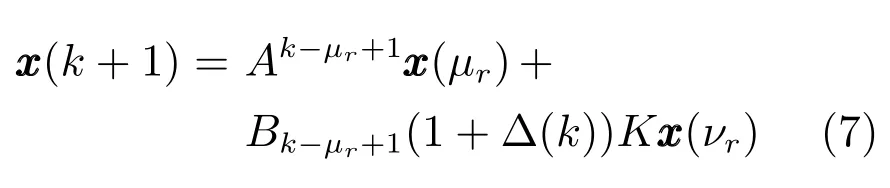
取如下擴展狀態變量:

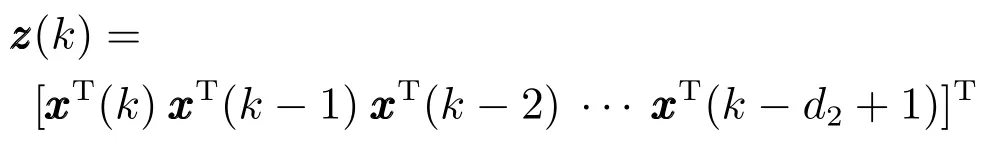
則系統(7)可改寫為如下的等價模型:

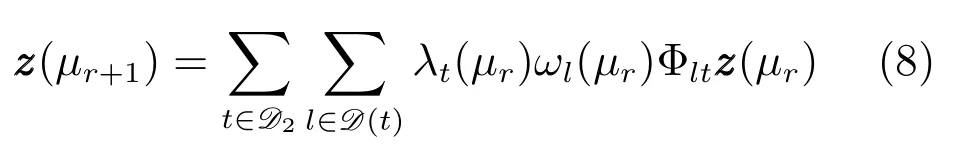
如果t=1,

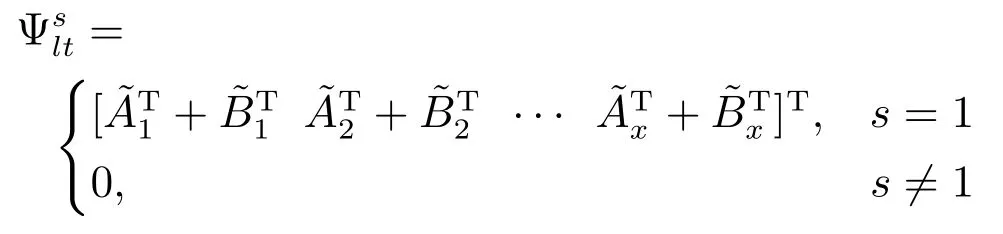
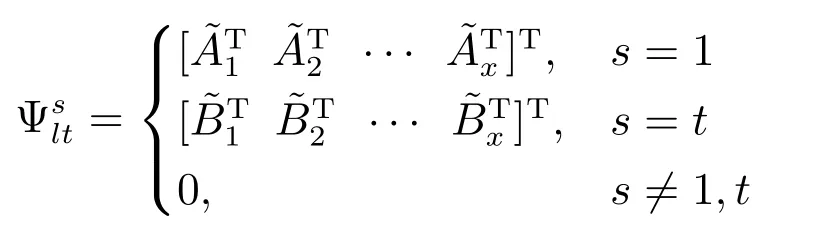
2 主要結果

2.1 單輸入情況

本文采用量化依賴Lyapunov函數方法設計保成本控制器及分析具有雙邊丟包量化反饋系統的穩定性.構造如下形式的Lyapunov函數:

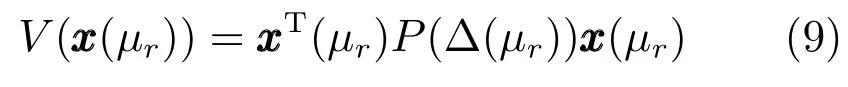
其中,P(?(μr))時變且依賴于量化誤差?(μr),有如下形式:

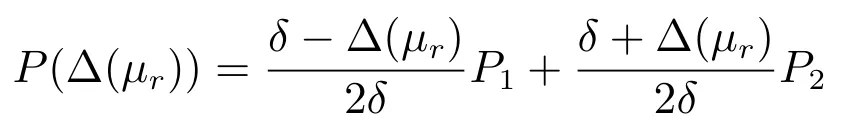
其中,P1和P2正定.保成本性能指標為

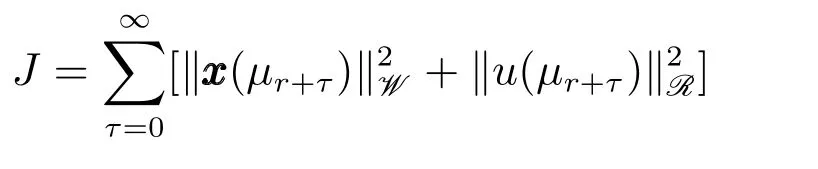
定理1.考慮如圖1中的離散時間系統及對數量化器(4),如果存在矩陣Q1＞0,Q2＞0,Y,Glt和γ滿足如下LMIs:

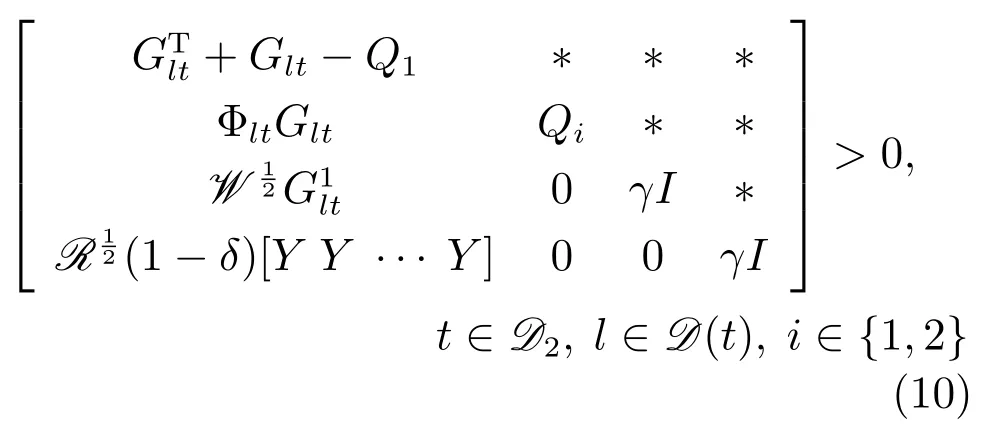
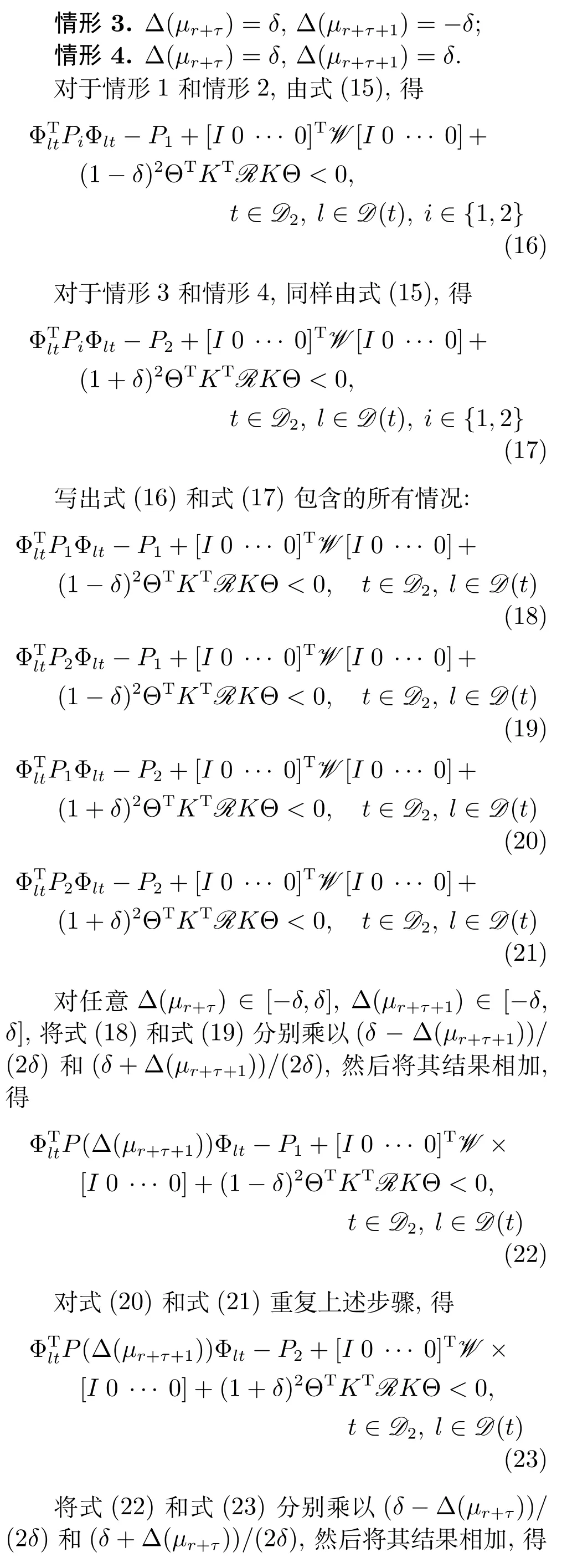
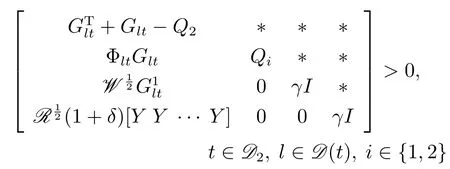
2.2 多輸入情況

以上考慮的是單輸入的情形,接下來將量化依賴Lyapunov函數方法拓展到多輸入的情況.同樣考慮線性離散時不變系統(1),其中系統輸入u(k)∈Rm,量化反饋為

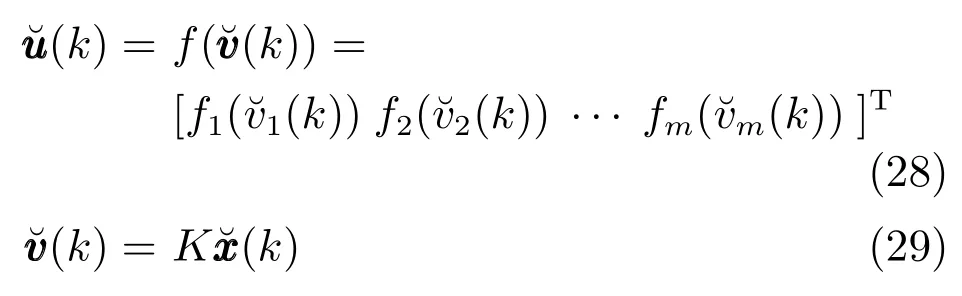
其中,fi(·)是量化器輸入v(k)的第i行對應的量化器.同樣假設fi(·)為式(4)中的對數量化器,則

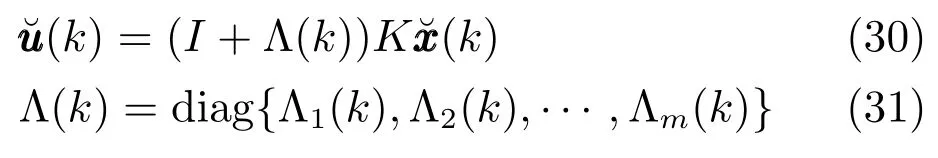
其中,Λi(k)∈[?δi,δi].可得系統閉環模型為

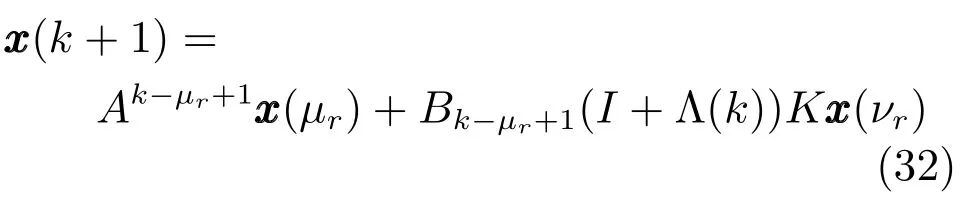
通過研究發現,式(31)中的Λ(k)可表示為

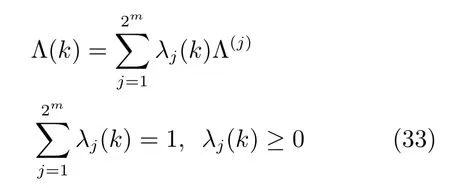
其中,Λ(j)是對角矩陣,只包含元素?δi或δi,2m種?δi或δi的組合得到所有的Λ(j).因此系統閉環模型(32)可轉化為

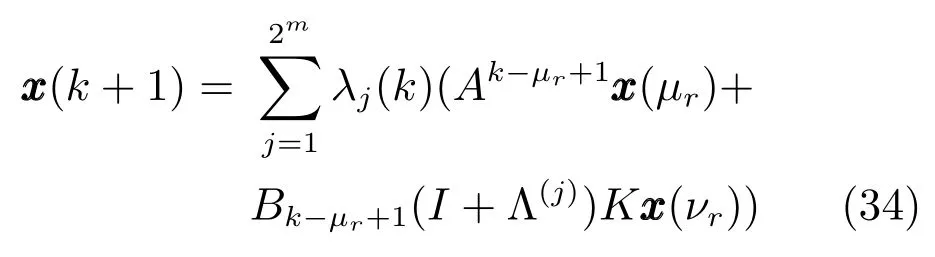
針對多輸入情況,設計保成本控制器及分析具有雙邊丟包量化反饋系統的穩定性,有如下定理:

定理2.考慮如圖1中的離散時間系統及對數量化器fi(·),如果存在矩陣Qi＞0,Qj＞0,Y,Glt和γ滿足如下LMIs:

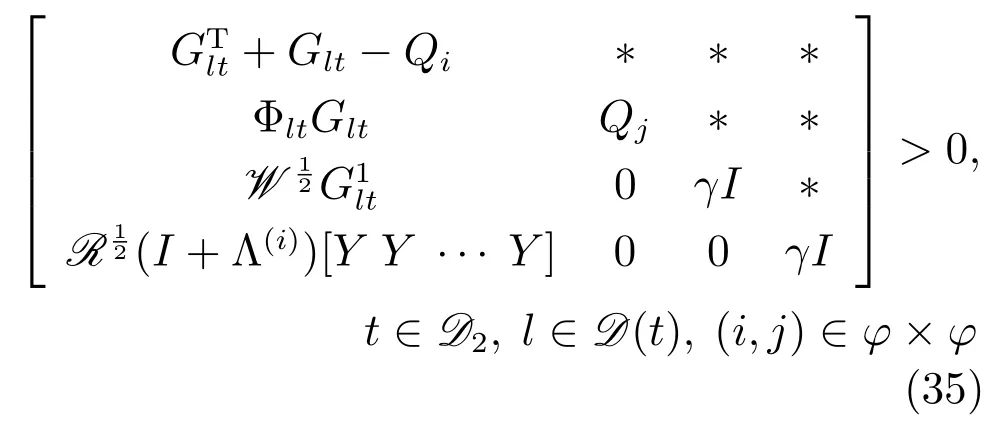
其中,?={1,2,···,2m}.那么,存在保成本控制器(28)使閉環系統(32)漸近穩定,且量化狀態反饋控制器為

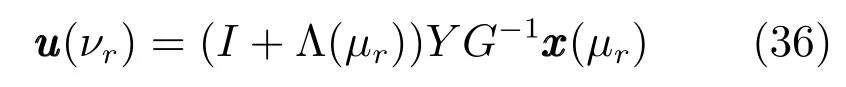
證明.構造形如式(9)的Lyapunov函數

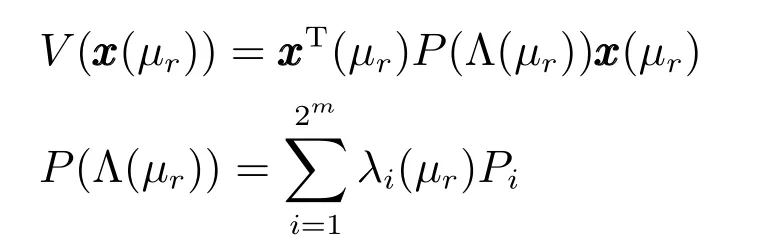
其中,矩陣Pi＞0,重復定理1的證明過程,可得

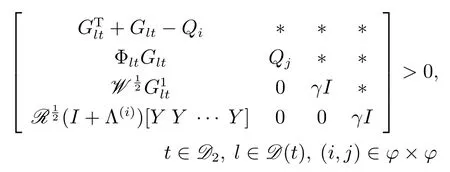
由此,對于任意 Λ(μr+τ)和Λ(μr+τ+1),有

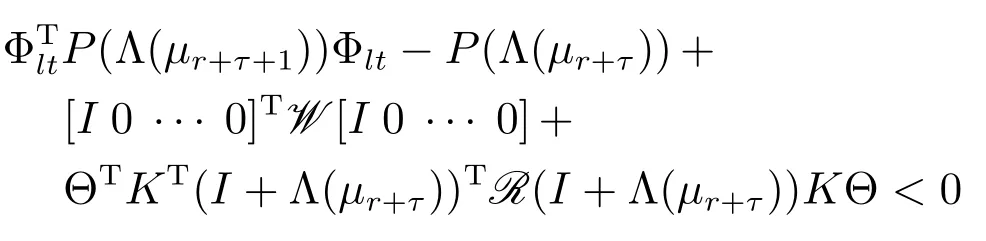
注2.本文所謂保守性更弱的結論主要是針對文獻[25]采用的二次型Lyapunov函數而言,即對整個量化誤差區間δ]取固定的Lyapunov矩陣P.而本文采用了新的量化依賴Lyapunov函數,,Lyapunov 矩陣依賴于量化誤差,即P(?(μr))=(δ??(μr))P1/(2δ)+(δ+ ?(μr))P2/(2δ),在定理1和定理2中,若取Q1=Q2=P,則本文的結論可退化為文獻[25]的結論.由此可知,本文的方法保守性更弱.

3 仿真例子

為驗證定理1,考慮如下單輸入線性離散時不變系統:

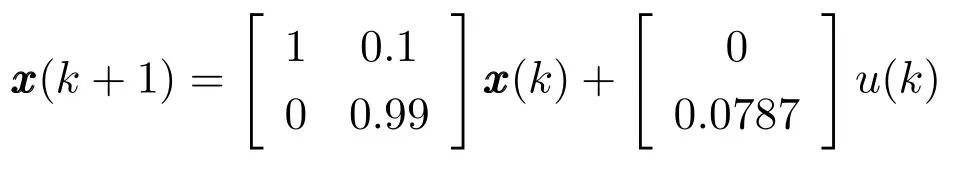
初始狀態為x(0)=[0.01 0]T,兩個通道丟包上界為d1=d2=3.

為驗證定理2,考慮如下多輸入線性離散時不變系統:

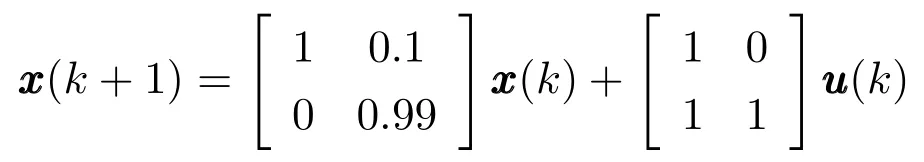
同樣,取初始狀態為x(0)=[0.01 0]T,兩個通道丟包上界為d1=d2=3.

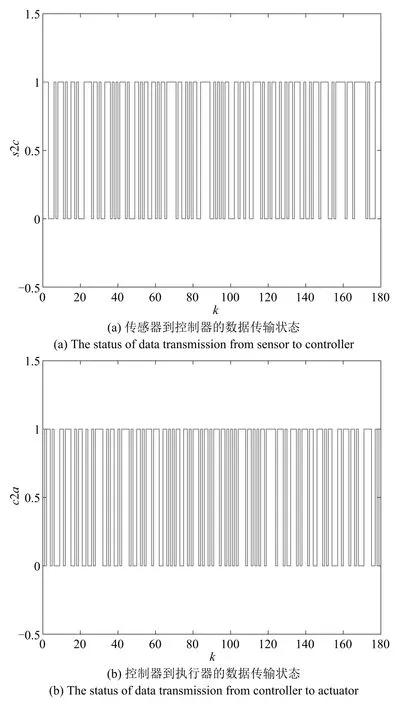
圖2 網絡環節的數據傳輸狀態Fig.2 The status of data transmission

系統網絡數據傳輸狀態如圖2所示,其中,s2c=1表示控制器從傳感器成功接收到數據,s2c=0則沒有收到數據,c2a=1表示執行器從控制器成功接收到數據,c2a=0則沒有收到數據.基于定理1和定理2,得到了在不同量化密度下的單輸入系統及多輸入系統的狀態響應和控制輸入仿真結果分別如圖3和圖4所示,并且列出其反饋增益K和性能指標J值如表1.由此證明了本文NCS保成本控制器設計方法的有效性.與文獻[25]中二次型Lyapunov函數方法相比,不論是單輸入系統還是多輸入系統,采用本文的量化依賴Lyapunov函數方法,可以較好地改善控制性能.此外,從仿真實驗結果來看,當量化密度取得較小時,即量化器較粗糙,可以得到文獻[25]中二次型Lyapunov方法不可行,而本文方法可以正常求解的結論,因此本文方法保守性更弱.

表1 兩種Lyapunov函數方法下的反饋增益K及性能指標J對比Table 1 Comparison of feedback gainKand performance indexJvalues using two Lyapunov function methods

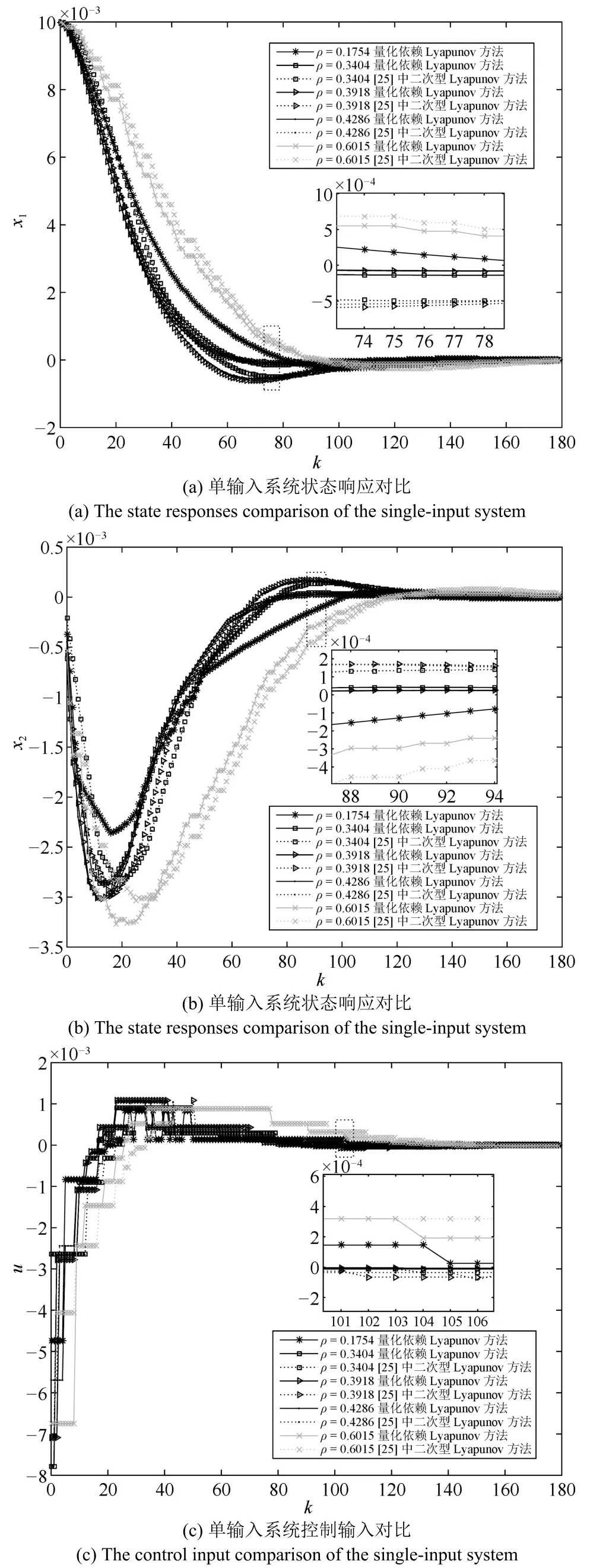
圖3 單輸入系統狀態響應及控制輸入Fig.3 The state responses and control input of the single-input system

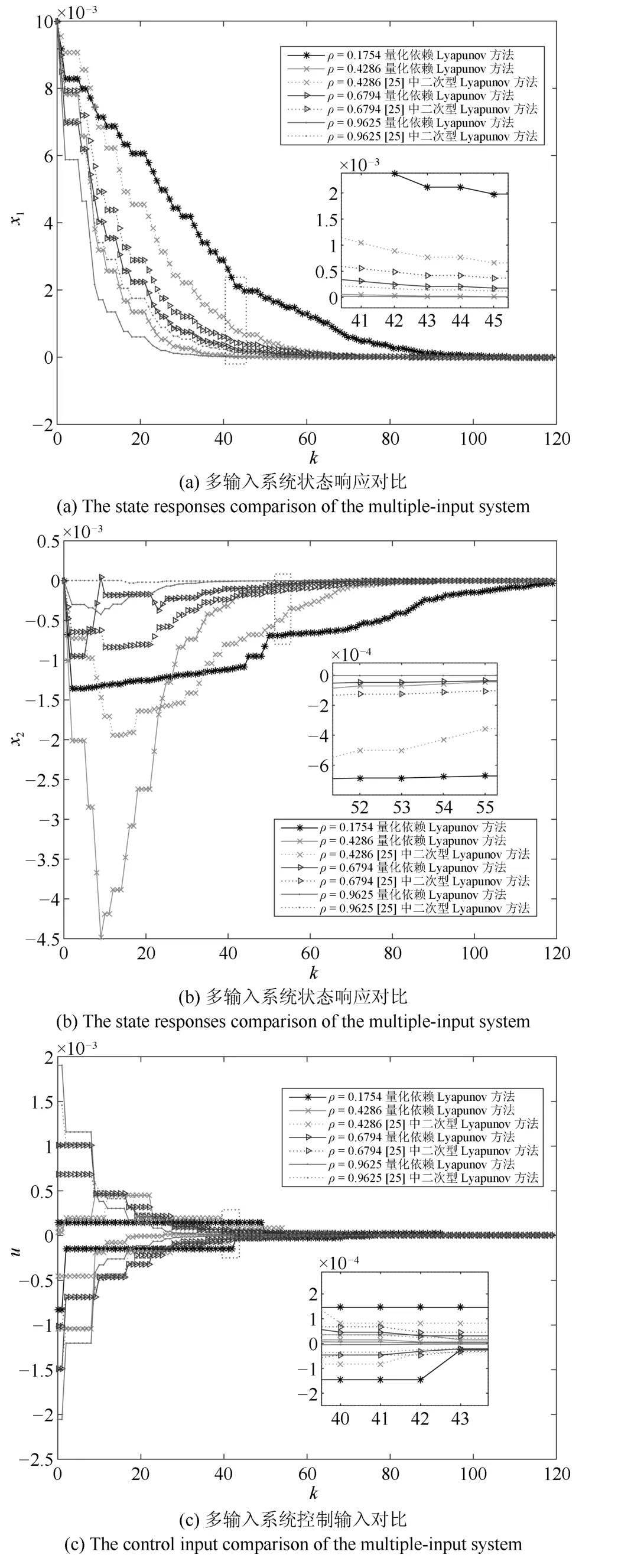
圖4 多輸入系統狀態響應及控制輸入Fig.4 The state responses and control input of the multiple-input system

4 結論

本文的主要目標是給出丟包網絡系統的保成本控制器設計方法,該方法的關鍵在于運用量化依賴Lyapunov函數來分析閉環系統的穩定性.本文基于魯棒控制理論建立了包含對數量化器的網絡控制系統數學模型,得到了系統魯棒穩定的充分條件和保成本控制器.仿真結果證明了設計方法的有效性和合理性,并通過和文獻[25]中二次型Lyapunov函數方法的比較,說明了運用量化依賴的Lyapunov函數方法得到的結果保守性更弱.但同時也由于該Lyapunov函數引入了更多的決策變量,使得本文方法付出了更大計算量的代價.