基于映射字典學習的跨模態(tài)哈希檢索
姚濤 孔祥維 付海燕 TIAN Qi
隨著計算機網(wǎng)絡和信息技術的快速發(fā)展,網(wǎng)絡上的媒體數(shù)據(jù)量急劇增長,媒體的表示形式也呈現(xiàn)出多模態(tài)性(圖像、文本、聲音、視頻等).例如:在微博上傳照片時,往往會同時上傳一段文字描述照片的內(nèi)容或用一些標簽標注圖像的內(nèi)容;在微信的朋友圈分享時,往往也是圖文并茂;購物網(wǎng)站,例如淘寶、京東等,在描述產(chǎn)品信息時通常既用圖片,又用文字.這些多模態(tài)數(shù)據(jù)雖然表現(xiàn)形式不同,但它們之間存在語義關聯(lián).跨媒體檢索的目的就是挖掘不同媒體之間存在的語義關系,并按語義關系進行排序,返回跟查詢存在較強語義關系的不同模態(tài)的數(shù)據(jù).隨著媒體數(shù)據(jù)量的急速增長和模態(tài)的多樣化,傳統(tǒng)的檢索方法已經(jīng)不能滿足當前跨媒體檢索的需求.如何在海量數(shù)據(jù)中檢索不同模態(tài)的數(shù)據(jù)成為一個巨大的挑戰(zhàn).
哈希方法是解決大數(shù)據(jù)問題的一種有效的方法,不僅能大大節(jié)省存儲空間,而且計算效率也大幅提高.例如一張圖片用5000維的BOW表示,假設每維用double數(shù)據(jù)類型表示,即每維占用8Bytes的存儲空間,則需要5000×8Bytes=40000Bytes的存儲空間.而哈希方法是把數(shù)據(jù)映射漢明空間,例如用32bits(8bits=1Byte)來表示一張圖片,僅需要4Bytes的存儲空間,大大節(jié)省了存儲空間,占用的存儲空間僅為原始特征空間的萬分之一.在檢索過程中,因為數(shù)據(jù)用二值碼表示,因此在計算樣本間的距離時,只需要做簡單的異或操作即可,大大提升了計算的效率,使檢索的時間復雜度遠低于傳統(tǒng)方法.
針對以上問題,本文提出一種基于映射字典學習的跨媒體哈希算法,主要貢獻如下:
1)利用映射字典學習使哈希碼含有語義信息以提升算法的性能.算法同時學習了哈希函數(shù),這與現(xiàn)存的字典學習哈希算法不同.
2)提出通過最小化量化誤差,學習一個正交旋轉矩陣,提升算法的性能,并且可以證明旋轉后的解依然是問題的局部最優(yōu)解.
本文結構安排如下:第1節(jié)介紹哈希算法的相關工作;第2節(jié)回顧字典學習的相關內(nèi)容,闡述了本文算法的思想,優(yōu)化過程及計算復雜度分析;第3節(jié)給出在兩個公開數(shù)據(jù)集上的實驗結果;第4節(jié)對本文的研究內(nèi)容進行總結.
1 相關工作
由于哈希方法的高效性和節(jié)省內(nèi)存,最近引起了越來越多的關注[1?15].哈希方法一般可以分為單模態(tài)哈希和多模態(tài)哈希.
單模態(tài)哈希方法又可以分為不依賴數(shù)據(jù)的哈希方法和依賴數(shù)據(jù)的哈希方法.在不依賴數(shù)據(jù)的哈希方法中,最先提出的是局部敏感哈希(Local sensitive hashing,LSH),它利用隨機線性映射作為哈希函數(shù),把原始空間中的樣本映射到漢明空間[1].但是,樣本之間的相似性是非線性的,線性函數(shù)很難捕捉樣本之間的內(nèi)在聯(lián)系,因此核局部敏感哈希(Kernelized local sensitive hashing,KLSH)提出利用核方法捕捉樣本之間的內(nèi)在聯(lián)系[2].但是,這類算法往往需要很長的哈希碼和多個哈希表才能取得較好的實驗結果.然而隨著哈希碼長度的增加,會降低相似樣本映射到同一個桶的概率,導致召回率的迅速降低,而且較長的哈希碼必然會增加存儲空間和計算復雜度.相對于不依賴于數(shù)據(jù)的哈希方法,依賴于數(shù)據(jù)的哈希方法可以獲得更為緊湊的表示,較小的碼長就可以獲得令人滿意的結果,因此受到越來越多的研究人員關注[4?8].譜哈希(Spectral hashing,SH)通過放松哈希函數(shù)的二值約束,利用譜圖分析和拉普拉斯特征函數(shù)學習哈希函數(shù)[4].核監(jiān)督哈希(Supervised hashing with kernels,KSH)利用核方法學習哈希函數(shù),在漢明空間最小化正樣本對之間的距離,最大化負樣本對的距離[5].以上算法取得較好的實驗結果,但是沒有考慮量化損失的影響,導致學習到的哈希函數(shù)的性能的下降.迭代量化哈希(Iterative quantization,ITQ)通過最小化量化誤差,學習一個旋轉矩陣,得到性能更好的哈希函數(shù)[6].監(jiān)督離散哈希(Supervised discrete hashing,SDH)提出了一種離散優(yōu)化算法,直接可以得到問題的離散局部最優(yōu)解[7].然而隨著網(wǎng)絡上多模態(tài)數(shù)據(jù)的不斷增長,一個網(wǎng)頁可以包含多種模態(tài)的數(shù)據(jù),而單模態(tài)的哈希方法通常不能直接用于多模態(tài)數(shù)據(jù),如何把多模態(tài)數(shù)據(jù)納入到一個統(tǒng)一的學習框架成為新的挑戰(zhàn).
多模態(tài)哈希方法一般分為多模態(tài)融合哈希方法和跨模態(tài)哈希方法,本文主要研究跨模態(tài)哈希方法.多模態(tài)融合哈希方法利用不同特征之間的互補性,學習一個更好的漢明空間,提升算法的性能[8?10].跨模態(tài)哈希的目標是學習一個共享的漢明空間,在這個空間可以實現(xiàn)跨媒體檢索[6,11?17].基于相似敏感哈希的跨模態(tài)度量學習方法(Cross-modality metric learning using similarity sensitive hashing,CMSSH)通過最小化不同模態(tài)的相似樣本之間的漢明距離,最大化不同模態(tài)的不相似樣本間的漢明距離,學習哈希函數(shù)[11].典型相關分析(Canonical correlation analysis,CCA)[18]哈希方法,把CCA引入跨媒體哈希方法,提出最大化模態(tài)間的相關性,學習一組哈希函數(shù)[6].然而上述方法只保持了模態(tài)間的相似性,忽視了模態(tài)內(nèi)的相似性.跨視角哈希(Cross view hashing,CVH)把譜哈希擴展到跨模態(tài)檢索,通過最小化加權距離,保持相似樣本(模態(tài)內(nèi)和模態(tài)間)的相似性[12].多模態(tài)潛在二值嵌入(Multi-modal latent binary embedding,MLBE)提出一個概率生成模型,通過保持多模態(tài)樣本的模態(tài)內(nèi)和模態(tài)間的相似度來學習哈希函數(shù)[16].然而,這些方法并沒有為不同模態(tài)的數(shù)據(jù)學習一個統(tǒng)一特征空間,導致無法捕捉不同模態(tài)間存在的一些潛在的共享信息.協(xié)同矩陣分解哈希(Collective matrix factorization hashing,CMFH)利用協(xié)同矩陣分解保持模態(tài)間的相似性,為樣本對學習同一表示[13].基于聚類聯(lián)合矩陣分解哈希(Cluster-based joint matrix factorization hashing,CJMFH)提出了首先對各個模態(tài)進行聚類運算,再利用矩陣分解同時保持模態(tài)內(nèi)、模態(tài)間和基于聚類的相似性[17].以上方法雖然取得了令人滿意的結果,但是學習到的哈希碼不包含任何語義信息,限制了算法的性能.稀疏哈希(Latent semantic sparse hashing,LSSH)為了縮小圖像和文本之間的語義鴻溝,利用稀疏表示學習圖像的一些顯著結構,利用矩陣分解為文本學習一個潛在的語義空間,并保持模態(tài)間的語義相似性[14].稀疏多模態(tài)哈希(Sparse multi-modal hashing,SMMH)提出利用稀疏表示為圖像和文本學習一個共同的語義空間,保持模態(tài)間的相似性[15].這類方法利用稀疏表示,使哈希碼包含語義信息,提升了算法的性能.但是這類算法通常存在以下問題,限制了算法的應用.1)在字典學習算法中,因為稀疏約束項的存在,導致訓練和測試過程算法的復雜度高.2)這些哈希算法不同于傳統(tǒng)的哈希算法,沒有學習顯式的哈希函數(shù).測試樣本,通常需要首先解決一個Lasso問題,得到樣本的稀疏表示,然后通過量化得到樣本的哈希碼(例如文獻[14]),而不能像傳統(tǒng)算法那樣直接利用哈希函數(shù)到.3)因為得到的系數(shù)矩陣是稀疏的,導致了哈希碼的0和1分配不均勻.
針對以上問題,本文提出一種基于映射字典學習的哈希算法.在字典學習過程中,放松了稀疏約束項算法,不僅降低了時間復雜度和平衡了哈希碼的分布,而且在字典學習過程中得到了哈希函數(shù).對于哈希問題的求解,現(xiàn)存的大部分跨模態(tài)哈希算法往往采用譜松弛的方法得到連續(xù)的最優(yōu)解[11,19],沒有考慮量化損失對算法性能的影響,而導致性能的下降[3].本文受ITQ的啟發(fā),通過最小化量化誤差,學習一個正交的旋轉矩陣,進一步提升算法的性能.
2 映射字典學習哈希算法(DPLH)
本節(jié)首先介紹字典學習的基本內(nèi)容和本文提出的基于映射字典學習的哈希算法,然后引出優(yōu)化算法及正交變換的相關內(nèi)容,最后分析算法的時間復雜度,證明算法的高效性.
2.1 映射字典學習
字典學習已經(jīng)在圖像處理和計算機視覺領域取得了巨大的成功[20?28].傳統(tǒng)的字典學習可以分為綜合字典學習和分析字典學習兩類.綜合字典學習應用在各個領域取得了令人滿意的成果[21?27],而分析字典學習的研究正處在起步階段[28].
綜合字典學習的目標函數(shù)一般定義為
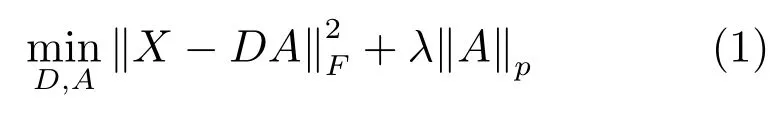
其中,X∈Rd×N表示數(shù)據(jù),D∈Rd×c表示字典(字典的每行D(:,i)稱為字典的一個原子),A∈Rc×N表示系數(shù)矩陣,λ為權重參數(shù),‖·‖F(xiàn)表示Frobenius范數(shù),一般情況下取p=1,即l1范數(shù).式(1)表明數(shù)據(jù)X可以由字典和稀疏的系數(shù)矩陣重構.
分析字典學習目標函數(shù)一般定義為
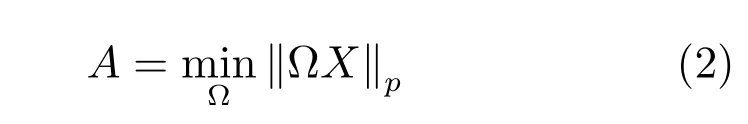
這里的范數(shù)可以為l1或l2范數(shù),A為稀疏矩陣,?表示字典.
然而,在字典學習過程中加入l1或l2稀疏約束項,往往會導致過大的計算量.文獻[27]把綜合字典學習和分析字典學習納入同一個學習框架,提出了一種基于映射字典學習的分類方法,利用線性映射代替非線性的稀疏編碼,取得了令人滿意的結果.受此啟發(fā),本文利用線性映射的方法來進行字典學習,以減少時間復雜度,同時把學習的線性映射作為哈希函數(shù).映射字典學習的目標函數(shù)定義為
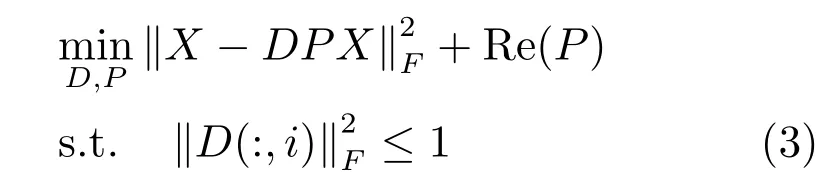
其中,Re(·)表示正則項,P可以看作重構矩陣.
2.2 DPLH算法的思想
在描述DPLH算法之前,先對本文用到的符號進行說明.為了描述方便,本文只考慮兩種模態(tài),例如:圖像和文本,當然算法可以很容易擴展到多于兩種模態(tài)的情況.用X(k)={x(1k),x(2k),···,x(Nk)}表示第k個模態(tài)的特征描述,k=1,2.X(k)∈Rdk×N,{x(i1),x(i2)}表示第i個樣本由不同模態(tài)描述構成的樣本對.其中,dk表示第k個模態(tài)的特征空間的維數(shù),N表示樣本對的數(shù)量.用Ak∈Rc×N表示第K個模態(tài)的系數(shù)矩陣,Dk∈Rdk×c表示第k個模態(tài)的字典,Pk∈Rc×dk表示第k個模態(tài)的哈希函數(shù)(即上面提到的重構矩陣),B(k)∈{0,1}c×N表示第k個模態(tài)的哈希碼,其中c表示哈希碼的長度.本文把兩個模態(tài)納入到一個學習框架中,則映射字典學習算法的目標函數(shù)定義為
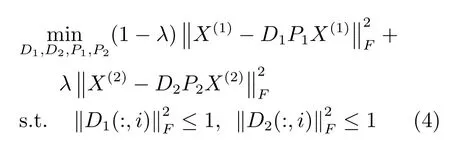
其中,前兩項是重構誤差,β,λ為權重參數(shù),D1(:,i)表示字典D1的第i個字典原子,D2(:,i)表示字典D2的第i個字典原子.
跨媒體檢索的目標是學習一個低維的共享子空間,異構數(shù)據(jù)之間的相似度可以在此空間直接度量.樣本對雖然用不同模態(tài)表示,但它們包含相同的語義信息,因此在學習的子空間中,它們的差異應該盡量小.文獻[13]把協(xié)同矩陣分解引入到子空間學習,但是樣本對在學習的子空間中相同表示的強約束條件,可能會導致算法性能的下降.因此,本文放松了此約束,目標函數(shù)定義為
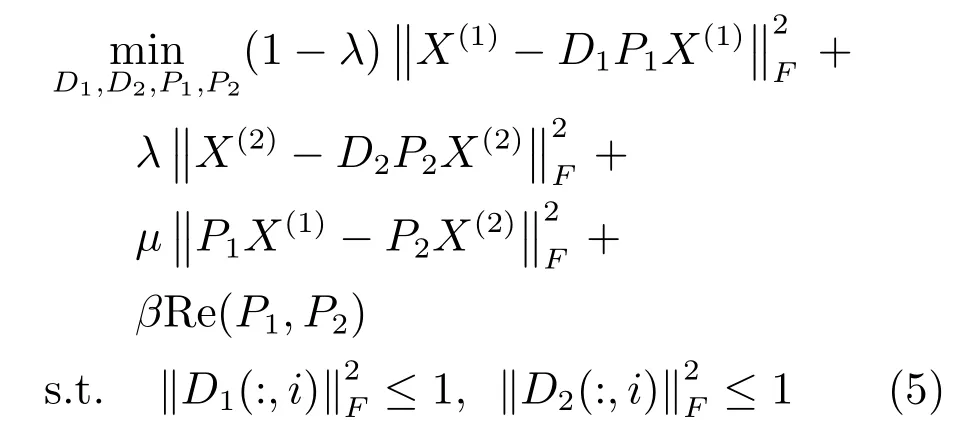
2.3 迭代優(yōu)化算法
為了更容易求解式(4),為兩個模態(tài)分別引入一個中間變量A1和A2,目標函數(shù)可寫為
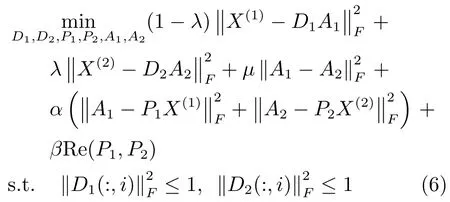
其中,參數(shù)α為權重.
式(6)的求解是一個非凸優(yōu)化問題.幸運的是,當求解一個變量而固定其他變量時,問題就變?yōu)橥沟?所以可以利用迭代的方法求解.
1)固定其他變量求解A1,則式(6)可寫為
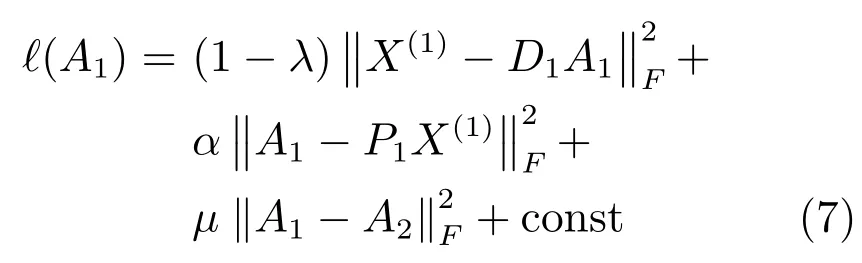
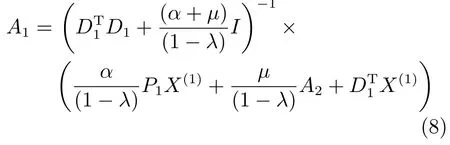
同理
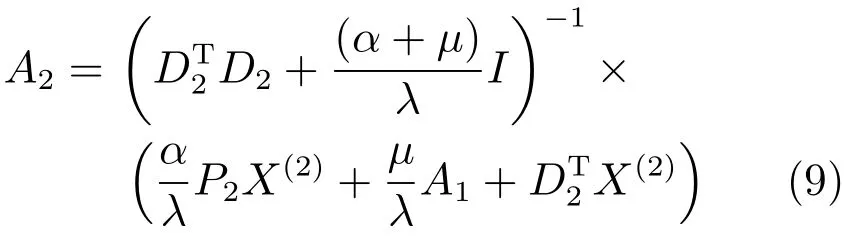
2)固定其他變量求解P1,則式(5)可寫為
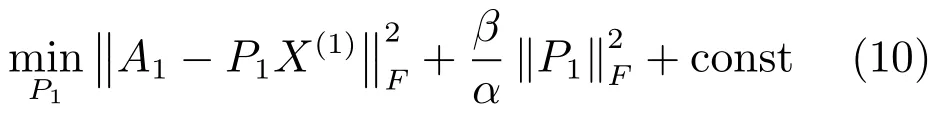
展開上式并對P1求導,令其導數(shù)為零,可以得到閉合解.
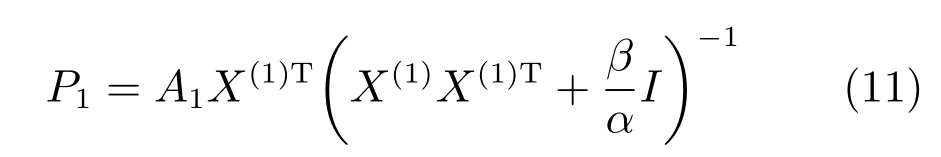
同理
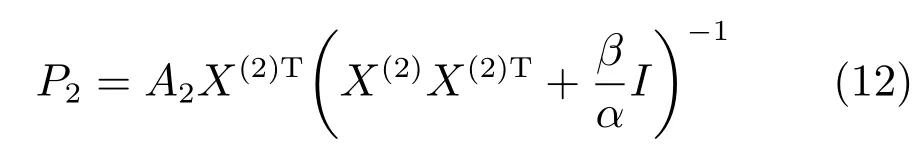
3)固定其他變量求解D1,則式(5)可寫為
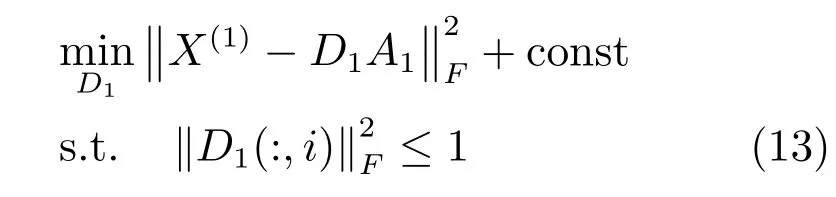
式(13)可以用文獻[27]提出的ADMM 算法求解,同理D2也可以用相同方法求解.
上述過程不斷迭代,直到目標函數(shù)收斂為止.
2.4 學習正交旋轉矩陣
在得到哈希函數(shù)P1,P2后,測試樣本的哈希碼可以通過哈希函數(shù)直接得到.
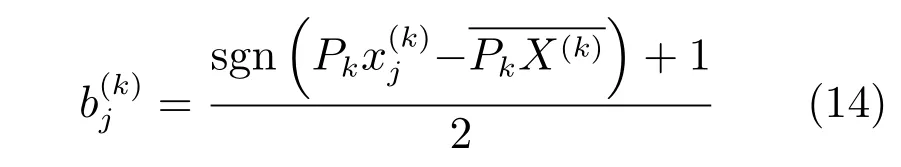
其中,sgn(·)表示符號函數(shù),表示第k個模態(tài)映射到子空間的樣本均值.在這里減去均值是為了保證哈希碼0和1分布均勻.
式(14)表示對于Pk的任意一行Pk(i),如果滿足,則,否則.然而式(14)的量化運算會帶來量化損失,而損失的大小會直接影響算法的性能,通常量化損失越小越好.但是,大部分現(xiàn)存的哈希算法,直接利用式(14)得到哈希碼,而沒有考慮量化損失對哈希函數(shù)性能的影響[1?5,13?14,19].文獻[6]提出了通過最小化量化誤差學習一個旋轉矩陣,以得到性能更好的哈希函數(shù),提升了算法的性能.受此啟發(fā),本文得到哈希函數(shù)P1,P2后,通過最小化量化誤差,學習一個正交變換矩陣,得到性能更好的哈希函數(shù).量化產(chǎn)生的損失定義為
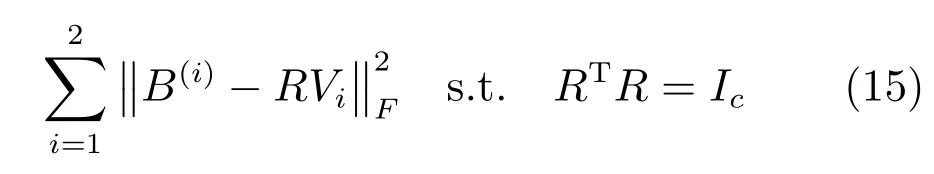
固定R,求B(i).
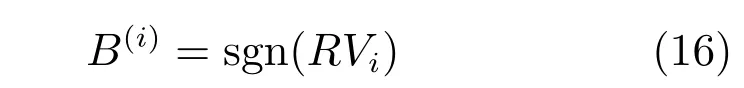
固定B(i),求R.
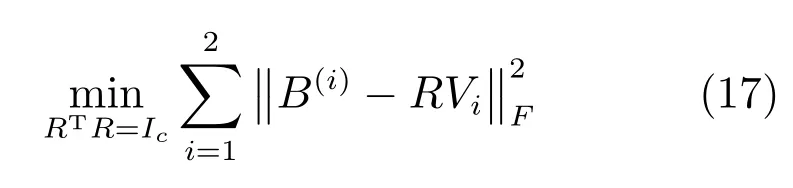
式(17)是典型的Orthogonal Procrustes problem,可以由奇異值分解(Singular value decomposition,SVD)的方法解決.為了最小化量化誤差,哈希函數(shù)更新為RPi.
下面證明RPi不僅可以最小化量化誤差,而且同時是目標函數(shù)(式(5))的局部最優(yōu)解,即正交不變定理.
定理1.設R是c×c的可逆正交變換矩陣,滿足RTR=Ic.如果P1,P2,D1,D2,A1,A2是式(6)的局部最優(yōu)解,則RP1,RP2,D1RT,D2RT,RA1,RA2也是式(6)的優(yōu)化解.
證明.
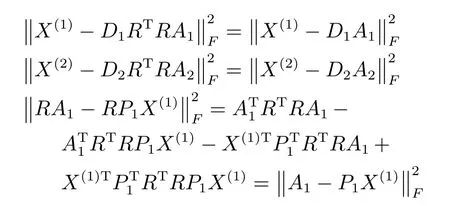
同理,
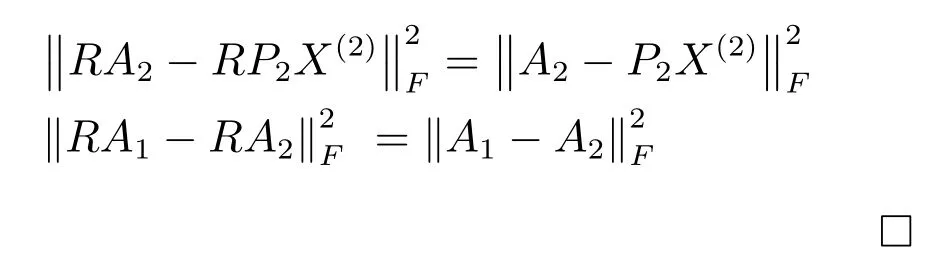
定理1證明了式(6)的局部最優(yōu)解并不是唯一的,存在正交變換矩陣R,使RPi也是式(6)的一個局部最優(yōu)解,因此直接優(yōu)化式(6)得到的解并不一定是問題的最優(yōu)解.本文通過最小化量化損失學習一個正交變換矩陣R,使得RPi既是式(6)的局部最優(yōu)解,又滿足量化損失最小,提升了算法的性能.
2.5 復雜度分析
在訓練過程中,計算復雜度包括兩部分:目標函數(shù)的求解和正交旋轉矩陣的求解.
目標函數(shù)的求解過程是迭代優(yōu)化的過程,不斷迭代更新P1,P2,D1,D2,A1,A2,直到算法收斂,因此訓練的計算復雜度主要產(chǎn)生在迭代更新過程.在這里,首先分析一下更新每個變量的計算復雜度.在更新變量Ai,i=1,2的表達式中,第1項計算復雜度為O(c2di+c3),第2項的計算復雜度為O(cdiN),因此更新Ai的計算復雜度為O(c2di+c3+cdiN+c2N).對于變量Pi,通過觀察發(fā)現(xiàn),Pi包含常數(shù)項(X(i)X(i)T+βI)?1,計算它們的時間復雜度為O(d2iN+d3i).但只需要在迭代前計算一次,并存儲,在迭代過程中,只需讀取即可,從而降低計算復雜度.因此迭代Pi的計算復雜度為O(cdiN+cd2i).利用ADMM 算法更新Di的計算復雜度為O(diN+c3+c2di+cd2i).
正交旋轉矩陣的求解也是利用迭代算法.其中,更新R首先要計算B(i)VT的SVD分解,即B(i)VT=S??ST,而R=?STS,所以總的計算復雜度為O(c2N+c3).而更新B(i)的時間復雜度為O(c2N).
在大數(shù)據(jù)時代,數(shù)據(jù)量非常大.通常在實際應用中N的值很大,一般情況下,N遠遠大于di和c的值.因此,整個迭代訓練過程的計算復雜度為O(N),即與訓練數(shù)據(jù)集的大小是線性關系.訓練過程的計算復雜度低,保證了算法的可擴展性.
而對于測試過程,因為本文生成了哈希函數(shù),測試樣本的哈希碼可以直接通過哈希函數(shù)得到,所以兩個模態(tài)的計算復雜度分別為O(cd1)和O(cd2).而檢索過程為求哈希碼的距離,可以通過高效的異或運算實現(xiàn).因此,測試過程的計算復雜度也很低.
3 實驗結果
在實驗中,本文主要通過兩個檢索任務驗證算法的有效性:利用圖像檢索文本和利用文本檢索圖像.通過實驗結果發(fā)現(xiàn),本文提出的無監(jiān)督算法,在某些情況下取得了優(yōu)于監(jiān)督算法的性能,證明了算法的有效性.
PDLH有4個參數(shù),參數(shù)λ是一個平衡參數(shù),控制兩個模態(tài)的權重,在實驗中發(fā)現(xiàn)這個參數(shù)魯棒性較強,本文設置λ=0.5,表明兩個模態(tài)的重要性相同.參數(shù)α控制重構系數(shù)矩陣產(chǎn)生的損失的權重,此參數(shù)也具有一定的魯棒性,根據(jù)經(jīng)驗本文取α=0.3.參數(shù)μ是模態(tài)間相似性保持的權重,在跨模態(tài)檢索中μ的作用較大,因此應該取較大的值,根據(jù)經(jīng)驗本文設置μ=2.參數(shù)β是正則化項的權重,因此應該取較小的值,根據(jù)經(jīng)驗本文設置β=0.02.
為了驗證迭代優(yōu)化算法的有效性,本文在Wiki和NUS-WIDE數(shù)據(jù)集上進行了實驗(哈希碼長為32bits),實驗結果如圖1所示.通過圖1發(fā)現(xiàn)本文提出的優(yōu)化算法收斂速度很快,在少于20次迭代后便收斂,說明了優(yōu)化算法的有效性.
3.1 實驗數(shù)據(jù)集
本文在Wiki[29]和NUS-WIDE[30]兩個公開數(shù)據(jù)上進行實驗,并與現(xiàn)存算法比較,以驗證本文算法性能.
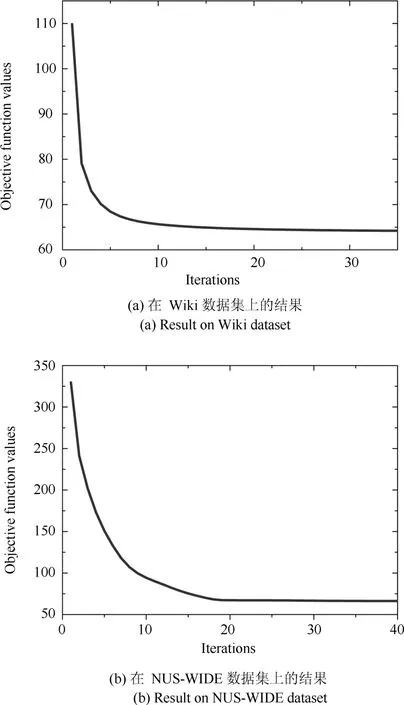
圖1 算法的收斂性分析Fig.1 Convergence analysis of the proposed optimization algorithm
Wiki數(shù)據(jù)集:包含2866個文檔,這些文檔是從維基百科收集的,每個文檔由一張圖片和描述它的一段文本組成,這些文檔可以分為10類.數(shù)據(jù)集中每張圖片用128維的BOW特征向量表示,而每段文本用10維的Latent Dirichlet allocation(LDA)特征向量表示.其中,隨機選擇75%的文檔構成訓練集,剩余的25%構成測試集.
NUS-WIDE數(shù)據(jù)集:包含269648張圖片,這些圖片是從Flickr上收集的.每張圖片與它對應的標注詞構成圖像–文本對,每張圖片平均有6個標注詞.這些樣本對被分為81個類,然而有些類的樣本數(shù)量很少,為了保證每類有足夠多的訓練樣本,本文選取了樣本數(shù)量最多的10個類,186577個樣本對.其中圖片用500維的BOW向量表示,而文本用1000維的BOW向量表示.參照文獻[13,19]的設置,本文從數(shù)據(jù)集中隨機選擇99%的圖像–文本對構成訓練集,剩余的1%構成測試集.
3.2 對比算法及評價標準
為了驗證PDLH算法的有效性,將PDLH與現(xiàn)有算法在兩個公開數(shù)據(jù)集上的實驗結果進行對比,現(xiàn)有算法包括CCA[6],CVH[12],CMFH[13],SCM[19],LSSH[14]和STMH[31].其中文獻[19]使用了兩種優(yōu)化算法:正交優(yōu)化算法和序列優(yōu)化算法,本文分別用SCM-O和SCM-S表示.并且SCM算法利用標簽建立相似矩陣,所以為監(jiān)督的跨模態(tài)哈希算法,而其他方法為無監(jiān)督算法.為了驗證本文提出的利用映射字典學習子空間方法的有效性,本文利用PDLH-表示去除旋轉矩陣的實驗結果.
在實驗中,因為STMH算法的代碼沒有公開,所以由我們實現(xiàn),而其余對比算法的代碼都由作者提供.所有代碼的參數(shù)都經(jīng)過調(diào)試,并且我們報告的是最好的實驗結果.在實驗中,本文以標簽作為判定標準,即兩個樣本的標簽至少含有一個相同的類,才判定這兩個樣本為同一類.
在實驗中,本文利用廣泛應用于哈希算法的Mean average precision(MAP)來評估各算法的性能.Average precision(AP)的定義如下:
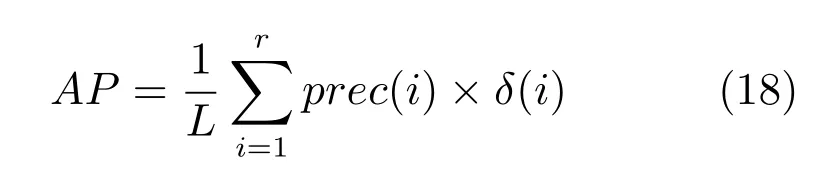
其中,r為檢索到的樣本數(shù)量,L為檢索到的正確樣本的數(shù)量,prec(i)為前i個樣本的準確率,δ(i)為指示函數(shù),當?shù)趇個樣本為正確樣本時δ(i)=1,否則δ(i)=0.而MAP為所有測試樣本AP的平均.
本文用每個測試樣本檢索返回的前200個樣本計算MAP,記為MAP@200.為了進一步證明PDLH的有效性,本文繪制了Precision-recall(PR)曲線圖,PR曲線反映了不同正確樣本召回率對應的準確率.
3.3 Wiki數(shù)據(jù)集的實驗結果
由于Wiki數(shù)據(jù)集較小,所以本文利用所有訓練集的樣本訓練哈希函數(shù).在實驗中,本文測試了不同哈希碼長的算法性能,其中MAP的實驗結果見表1.從表1可以看出,1)PDLH,CMFH和SCM-S算法的性能較好,PDLH在大多數(shù)碼長取得了最好的實驗結果,只在少數(shù)碼長低于SCM-S或CMFH的性能;2)在所有碼長情況下,PDLH的結果都優(yōu)于PDLH-的結果.這證明了正交旋轉矩陣通過最小化量化誤差提升了算法的性能;3)即使在去除旋轉矩陣的情況下,本文提出的算法也取得了良好的性能.這說明利用映射字典學習不僅降低了算法的時間復雜度,而且通過字典學習,使哈希碼含有語義信息,增強了哈希碼的區(qū)分能力,因此得到了令人滿意的實驗結果.
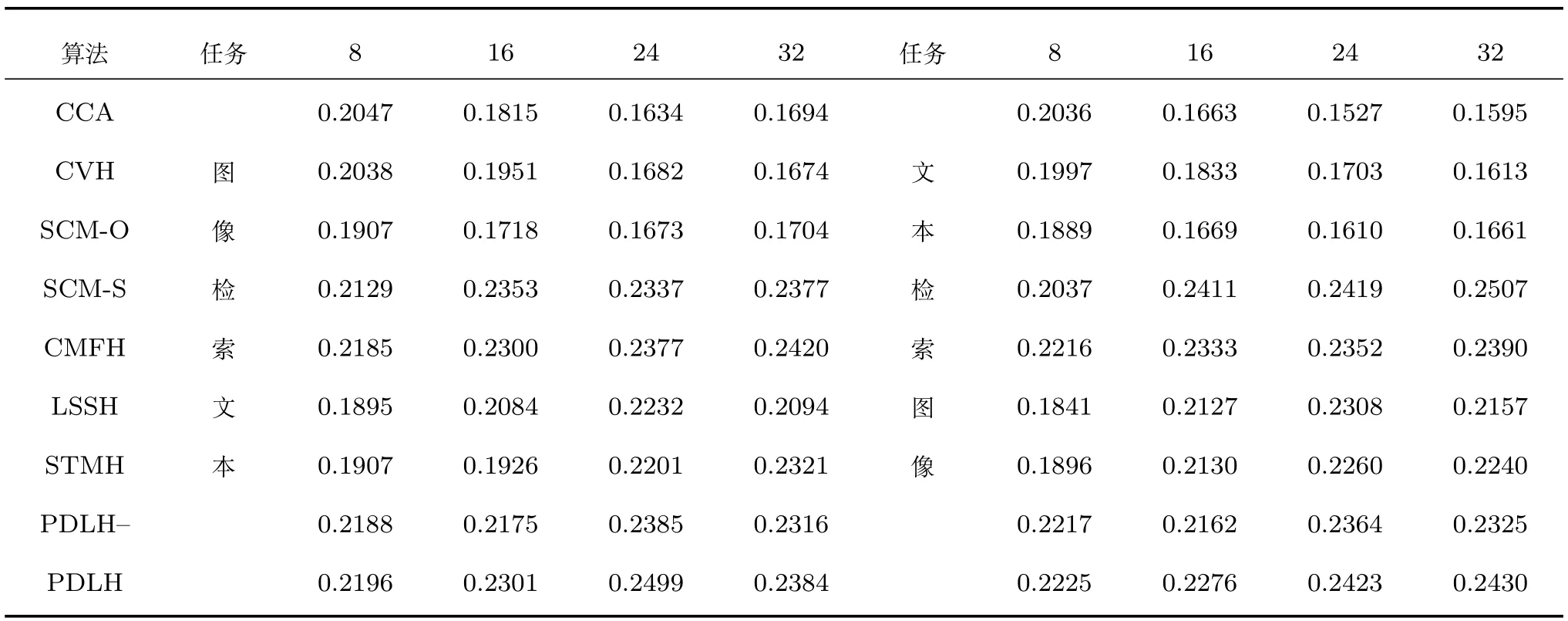
表1 圖像檢索文本和文本檢索圖像任務在Wiki數(shù)據(jù)集上的實驗結果(MAP@200)Table 1 MAP@200 results on Wiki dataset for the tasks of using the image to query texts and vice versa
SCM-S是監(jiān)督哈希算法,在哈希函數(shù)學習過程中不僅利用了特征信息,而且利用了所有樣本的標簽信息來獲得更好的哈希函數(shù).然而,獲得所有樣本的標簽,要耗費大量的人力物力,在大數(shù)據(jù)時代,是不可能實現(xiàn)的,所以本文算法更具有應用價值.
為了進一步證明本文提出算法的有效性,圖2和圖3分別繪制了碼長為16bits和32bits時各個算法在兩個任務上的的PR曲線圖.從圖2和圖3可以看出,PDLH和SCM-S算法取得了較好的性能,而PDLH在召回率較低時性能更好一些.這在實際應用中非常重要,因為用戶在檢索時,往往更關注排列在前的返回樣本.
3.4 NUS-WIDE數(shù)據(jù)集的實驗結果
由于NUS-WIDE的訓練集較大,而LSSH和SCM-O需要大量的訓練時間.為了降低時間復雜度,參照文獻[13]的參數(shù)設置,本文從訓練集中隨機選出5000個樣本對構成訓練集,而測試集包含的1%的樣本對全部用作測試.MAP的實驗結果見表2.從表2可以看出,在圖像檢索文本任務中,PDLH在各碼長都得到了最好的結果,而且性能明顯優(yōu)于其他算法.而在文本檢索圖像任務中PDLH和監(jiān)督算法SCM-S取得了明顯優(yōu)于其他算法的結果.而且即使在去掉旋轉矩陣的情況下,本文算法依然在大多數(shù)情況下取得了最好結果.實驗結果再次證明了算法既降低了復雜度,又提升了子空間的區(qū)分能力.同時也驗證了使哈希碼含有語義信息提升了算法的性能(在大部分情況下,性能超過監(jiān)督算法SCM-S,其余情況下,性能逼近監(jiān)督算法SCM-S).
為了進一步證明本文提出算法的有效性,圖4和圖5分別繪制了碼長為16bits和32bits時各個算法在兩個任務上的的PR曲線圖.從圖4和圖5可以看出,與MAP的結果類似,PDLH算法和監(jiān)督算法SCM-S的性能在NUS-WIDE上明顯優(yōu)于現(xiàn)有其他的無監(jiān)督算法.而與監(jiān)督算法SCM-S相比,PDLH在召回率較低時性能較好,這與在Wiki數(shù)據(jù)集上的結果類似.
為了進一步驗證本文算法的可擴展性,本文設定哈希碼碼長為16bits,并對訓練集的大小進行了不同設定,訓練時間和MAP的實驗結果見表3所示.從表3可以看出,隨著訓練集樣本數(shù)量的增加,算法的性能不斷提升.這是很合理的,因為隨著訓練集樣本數(shù)量的增多,訓練樣本包含樣本間的內(nèi)在聯(lián)系信息越豐富,因此可以學習更好的哈希函數(shù).而且通過表3還發(fā)現(xiàn)訓練時間與樣本的尺寸基本呈線性關系,從實驗上驗證了本文之前的復雜度分析.
4 結論
針對哈希碼語義無關而導致性能下降的問題,本文提出了一種基于映射字典學習的跨模態(tài)哈希檢索算法.算法利用映射字典學習降低了算法復雜度,并生成了哈希函數(shù),這與現(xiàn)存字典學習哈希方法不同.最后在兩個公開數(shù)據(jù)集上的實驗結果證明了算法的有效性.將來的工作主要包括學習一個更好的子空間表示,減小量化誤差對哈希函數(shù)的影響和利用非線性變換更好地捕捉樣本間的內(nèi)在聯(lián)系.
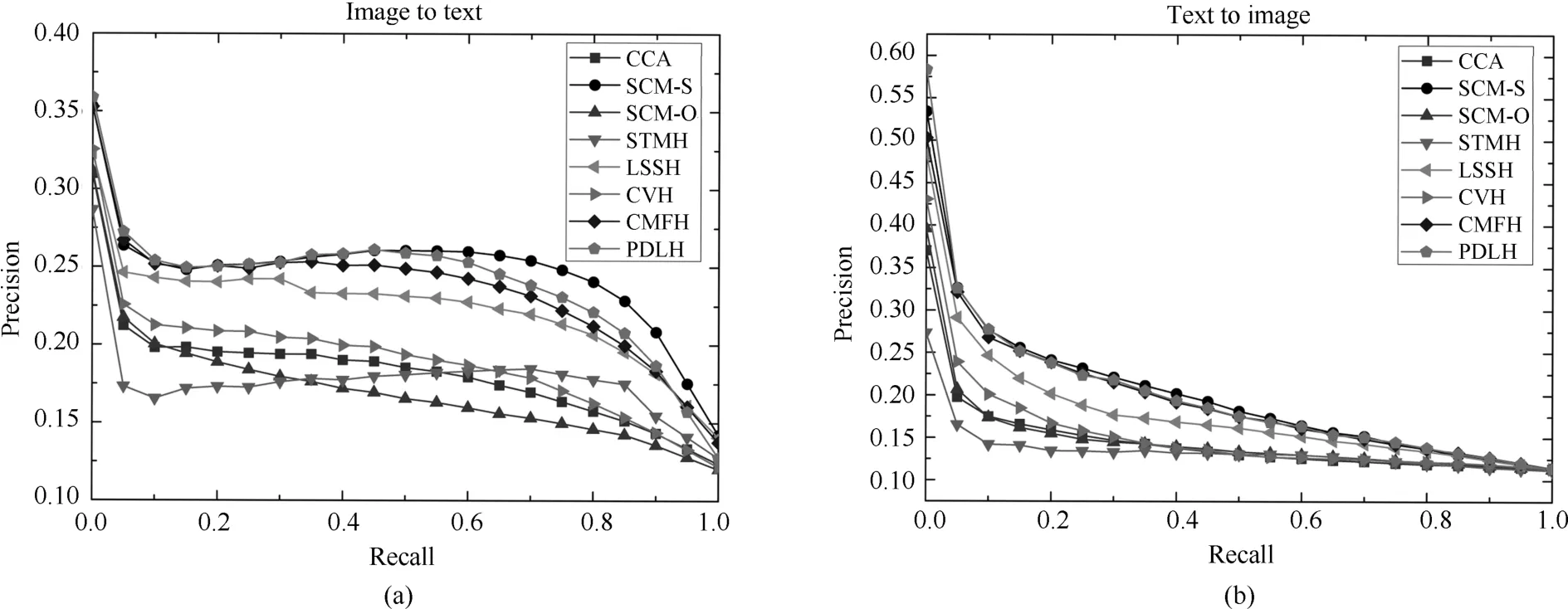
圖2 碼長16bits在Wiki數(shù)據(jù)集的PR曲線圖Fig.2 PR curves on Wiki dataset with the code length fixed to 16bits
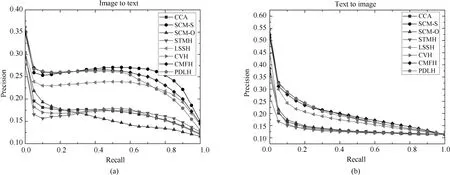
圖3 碼長32bits在Wiki數(shù)據(jù)集的PR曲線圖Fig.3 PR curves on Wiki dataset with the code length fixed to 32bits
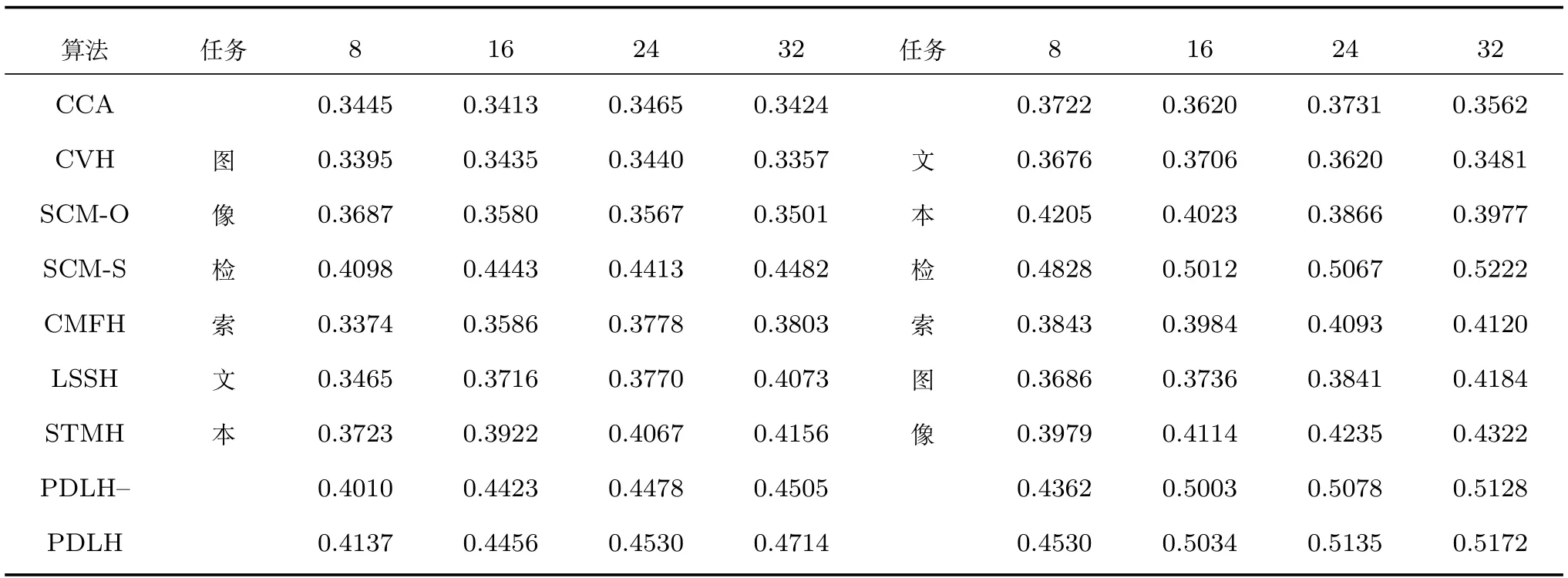
表2 圖像檢索文本和文本檢索圖像任務在NUS-WIDE數(shù)據(jù)集上的實驗結果(MAP@200)Table 2 MAP results on NUS-WIDE dataset for the tasks of using the image to query texts and vice versa(MAP@200)
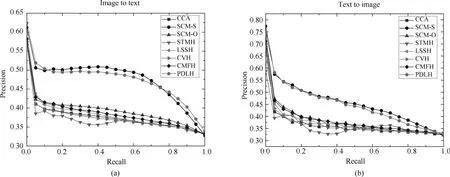
圖4 碼長16bits在NUS-WIDE數(shù)據(jù)集的PR曲線圖Fig.4 PR curves on NUS-WIDE dataset with the code length fixed to 16bits
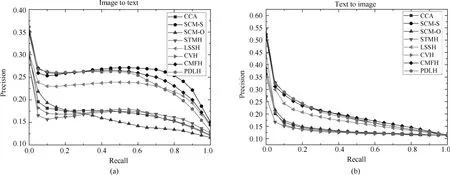
圖5 碼長32bits在NUS-WIDE數(shù)據(jù)集的PR曲線圖Fig.5 PR curves on NUS-WIDE dataset with the code length fixed to 32bits
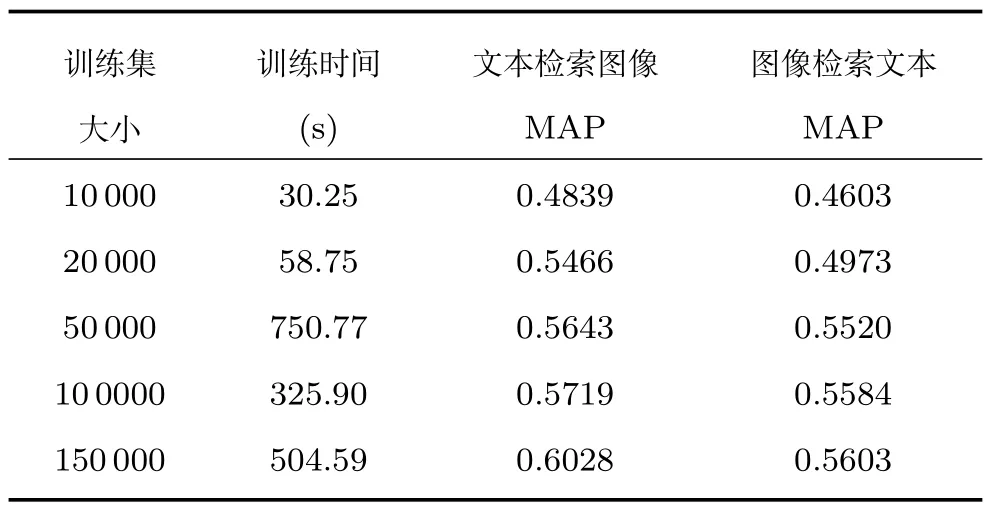
表3 不同數(shù)量訓練樣本的訓練時間(s)和MAP結果Table 3 The time costs(s)and MAP results with different sizes of training dataset

