試析運用聯想思維解決數學問題
◆徐慧鑫
(本溪市高級中學)
很多人說,高中數學知識抽象復雜,學習起來難度太大。我認為,高中數學之所以學習吃力,很重要的原因是缺乏有效的解題思路和解題方法。在實際學習中,我們在老師的帶領下經常會學習總結一些解題方法,但是解題思路的歸納學習往往被忽略。數學知識之間其實是有內在聯系的,新舊知識可以進行遷移與轉化,因此在數學學習中我們可以借助聯想思維,做好新舊知識的融會貫通。我認為,要想學好數學,就必須具備聯想思維。
一、什么是聯想思維
從字面上理解聯想,就是由之前認知的事物聯想到另一件事物上,借助兩者的關聯去思考探究新問題。在高中數學學習中,聯想可以將數學對象和有關知識進行聯系,由此到彼,找到兩個事物之間共有的規律,聯想是數學思路轉化的橋梁,是新舊數學知識聯系的紐帶。我們在學習中遇到陌生的習題,陌生的知識,都需要借助聯想,進行新舊知識的遷移。通過找關系,找到共有的規律,找到解題的思路。我在高中數學學習中很喜歡用聯想思維,對題設中的條件、圖形特征及求解目標進行分析,從而很快地聯想到原有的定義、定理和法則等,從而找到解題的思路和方法。運用數學聯想思維,數學解題可以達到事半功倍的效果。
二、數學聯想思維在數學解題中的作用
在筆者看來,在數學解題中善用聯想思維,可以起到撥開迷霧的積極作用。我通過自身的學習體驗將數學聯想思維的解題作用歸為兩類。
(一)數學聯想為數學解題指明方向
我們在數學學習的過程中總會遇到不懂的地方,無法繼續解答下去的情況,我們不知道怎么入手,如何破解這道題目,有這種體會主要是我們遇到的數學問題與我們之前學過的知識和嘗試過的題型不一樣,和我們掌握的解題方法無法關聯,我們就陷入解題的迷茫之中。在這種情況下,我們決不能鉆牛角尖,我們必須跳出來,換個思路,想想我們學過的類似的知識,去嘗試著建立新舊知識的關聯,通過“他山之石”,起到“可以攻玉”的目的。甚至與它的反面進行對比,逆向思維,看看能不能有意外的解題思路。有時候換個思路,進行聯想,我們會發現山重水復疑無路,柳暗花明又一村,在我們不知道如何解答的時候,找到解題思路。
(二)數學聯想帶動題設到結論的轉化
在高中數學學習中,我們常常用到轉化方法,適當的轉化可以剝繭抽絲,變抽象復雜為簡單生動。不懂的枯澀的問題在轉化后可以變得更熟悉,我們學習解答起來也更容易。轉化與聯想是有著本質契合性的,無論怎樣轉化,都需要聯想輔助,我們只有運用聯想思維才能進行準確轉化。在高中數學學習中,我們也常常覺得一些解題思路和方法很妙,其實仔細分析,是因為他們運用了聯想思維,沒有墨守常規,通過分析題目的特點聯想到相似的問題上,運用之前的解題思路進行難題的破解。因此數學聯想帶動數學問題從題設到結論的轉化。
三、巧用聯想思維解題數學問題
(一)直接聯想,突破難題
在高中數學聯想思維中,直接聯想是最好理解的,直接聯想就是表面聯想,什么時候可以運用直接聯想呢,當數學題目中包含解題條件和公式信息,我們可以借助直白的數學概念進行數學聯想,在聯想的過程中找到正確的解題思路,直接聯想,帶來的是解題的高效與準確。直接聯想是數學學習中我們必須要運用的一種解題思路,因為其簡單而基礎。在平時的數學學習中,我們必須要熟記課本中的各種數學理論知識和概念定理,千萬不能混淆,只有基礎知識掌握到位,才能運用直接聯想解決數學問題。例如在學習集合知識后,我們遇到這樣的聯系題:已知兩個集合A= {X/X2≤1},B={b},當b為多少時,滿足A∪B=A。在這一練習題目中所運用到的是集合知識,由于A∪B=A,運用直接聯想很快得出答案。再例如問題:直線X+2y+3=0的斜率和在y軸上的截距是多少?我們可以根據方程式,運用直接聯想,關聯到一次函數問題上,根據題目中列出的條件,探討斜率及截距問題。這種題型最適合直接聯想,找到關聯點進行突破解題。
(二)類比聯想,舉一反三
類比聯想就是運用類比法將不同類型的學習對象結合起來分析,找到兩者的差異,通過新舊知識的遷移做好兩者對象,解題思路和解題信息的差異區分,從而舉一反三。我們在學習圖形結構及數學關系時可以運用類比聯想。例如,解答圖像問題時,可以畫出圖像,兩種圖像對比分析,找到兩個圖像之間在對稱性、特殊性及獨特性方面的差異。或者在一些數量關系問題解答中運用類比聯想。特別是在“等差”,“倍數”這類問題的解答中,挖掘不同數量對象的關聯性。高中數學中有很多知識點有相似性,我們可以運用類比聯想思維解決等差數列、雙曲線、橢圓等相關的數學問題。
(三)抽象聯想,化繁為簡
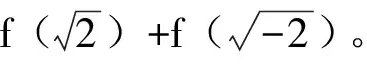
(四)對立聯想,結論驗證
在高中數學學習中,我們也應該掌握對立聯想,借助對立聯想來解決實際問題。題目信息可以是文字也可以是圖形,對立聯想難度很高,但是操作方便,我們在深入理解題目后,借助對立聯想解答。例如知道實數m,n,1,這三個實數之間的數量關系為m-n=8,mn+12+4=0。請求證m+n=0。如果采用正向思維很難找到問題解答的突破口,并且在正向思維思考中耗費大量時間。在正向思維無解的情況下,我們嘗試對立聯想。從證明結論入手:將m-n=8進行對立聯想,適當轉化后我們能得到m+(-n)=8,參考已知數量關系,可以得出m+(-n)=12+4,這樣就可以根據算式列出一個一元二次方程:X2-8X+12+4=0,從而解方程可以得出m,-n的值。結合題干,所以就可以進一步的得出Δ=(-8)2-4(12+4)≥0得出Δ=0,方程求解得出m=-n=4,可以證明結論。通過一系列的對立聯想,我們可以進行推理驗證結論。
四、結束語
聯想作為常見的數學思路,理應在高中數學學習中起到教學啟發與點撥的作用。我們在高中數學學習中必須做好聯想思維的嘗試運用。我們在學習初期很可能不知道如何運用聯想思維,也不知道運用哪一種聯想思維解決問題,但是我們在長期的數學解題嘗試中,在扎實的數學知識掌握的前提下,通過訓練,一定會熟練運用數學聯想思維解決數學實際問題。

