垂度阻尼索的設計及對結構減振的試驗研究1

禹見達,彭臨峰,張湘琦,彭 劍,陳政清

(1.湖南科技大學 土木工程學院,湖南 湘潭 411201; 2.湖南科技大學 結構抗風與振動控制湖南省重點實驗室，湖南 湘潭 411201;3.湖南大學 風工程與橋梁工程湖南省重點實驗室,長沙 410082)

隨著社會經濟的發展和技術的進步，各種高聳結構不斷涌現，如高聳的建筑結構[1]，大跨度橋梁[2-3]，大功率風電機塔[4]，大跨越輸電塔[5-7]，高聳的化工設備塔[8]，水上平臺塔架[9]等，這些結構或其中的部分構件由于柔度大、阻尼低，在地震、強風、波浪或其它激勵的作用下發生大幅振動甚至倒塌，造成國家經濟和人們生命、財產的重大損失。因此，對高聳結構進行減振控制得到了廣泛的關注。對高聳結構減振措施主要包括調頻質量阻尼器(TMD)減振和阻尼減振。

采用TMD對高聳結構進行風致振動控制被普遍采用。例如臺北101大廈，上海東方明珠電視塔，廣州新電視塔均采用TMD進行風振控制。陳永祁等[10]統計了國內外使用超過100 t的TMD的14項工程。但TMD對結構振動控制時受頻率比的影響非常大，實際結構在長期使用過程中，由于荷載、剛度的變化，結構的固有頻率會發生偏移，這將顯著削弱TMD對結構的減振效果。多重調頻質量阻尼器(MTMD)能改善TMD對結構振動控制的頻帶寬度，但其不能同時發揮所有質量塊的功效，需要有更大的質量比才能達到相同的減振效果[11]。主動質量阻尼器(AMD)能提高對結構振動的效果，但其可靠性及高成本使其應用受到了限制。TMD的本質是通過其本身慣性力平衡外部激勵對結構的作用，從而抑制結構的振動，但當結構可能發生多個不同頻率的振動時，TMD對結構振動控制效果難以保證。同時，隨著結構尺度的不斷增大，其基頻不斷減小，TMD所能提供的慣性力不斷減小，相同的質量比下其對結構的減振效果不斷下降。

采用阻尼器增加高聳結構的阻尼，是高聳結構減振最直接的一種方式。陳波等研究了輸電塔線體系基于磁流變(MR)阻尼器的風致振動控制。尹鵬等提出了一種橡膠鉛芯阻尼器用于輸電塔風振控制。樊禹江等采用壓電摩擦阻尼器進行了輸電塔結構中的振動控制研究。由于高聳結構各層之間變形小，結構上難以找到相互靠近并有較大相對位移的安裝位置來驅動阻尼器耗能減振，阻尼器的減振性能難以發揮，因此，目前未見直接采用阻尼器對高聳結構進行減振的工程實例。

高聳結構在大風作用下發生大幅振動，但結構在靠近地面處振幅小，振幅較大的位置遠離地面，為充分利用結構的大振幅驅動阻尼器耗能減振，作者開發了一種垂度阻尼索，可將阻尼力施加于結構的任意位置，利用結構與地面的相對位移，通過阻尼索的放大后驅動阻尼器運動耗能，本文為此展開研究。

采用塔架模擬高聳結構，在塔架與地面間安裝了垂度阻尼索對結構進行減振控制，因電渦流阻尼器具有制作簡便、黏性阻尼系數穩定且調節方便，同時還可以實現大行程和快速運動等特點而作為本試驗耗能元件。

1 垂度阻尼索對高聳結構減振原理

1.1 垂度阻尼索結構及其減振原理

垂度阻尼索包括主索、吊索、阻尼器和復位彈簧，垂度阻尼索結構如圖1所示。采用立柱和質量塊模擬高聳結構，在立柱頂部和錨碇間張拉主索ABC，主索上B點通過吊索將并聯的阻尼器和復位彈簧連接于主索與地面之間。當結構發生振動時，A處有微小的水平方向振動，主索B點豎向就發生較大的振動，二者關系為

y=βx

(1)

式中：y為主索與吊索連接點B的豎向位移(等于阻尼器運動的位移)；x為結構振動A處水平位移。忽略主索變形，位移放大系數β為

(2)

式中：L1為主索左跨度，f為主索垂度。由于β?1,并且隨著主索垂度的減小而增大。理論上主索在結構上的安裝高度不受限制，可選取結構振幅最大處連接主索，結構的微小振動就能驅動阻尼器產生較大的行程，增大阻尼器的耗能，從而減小結構的振動。

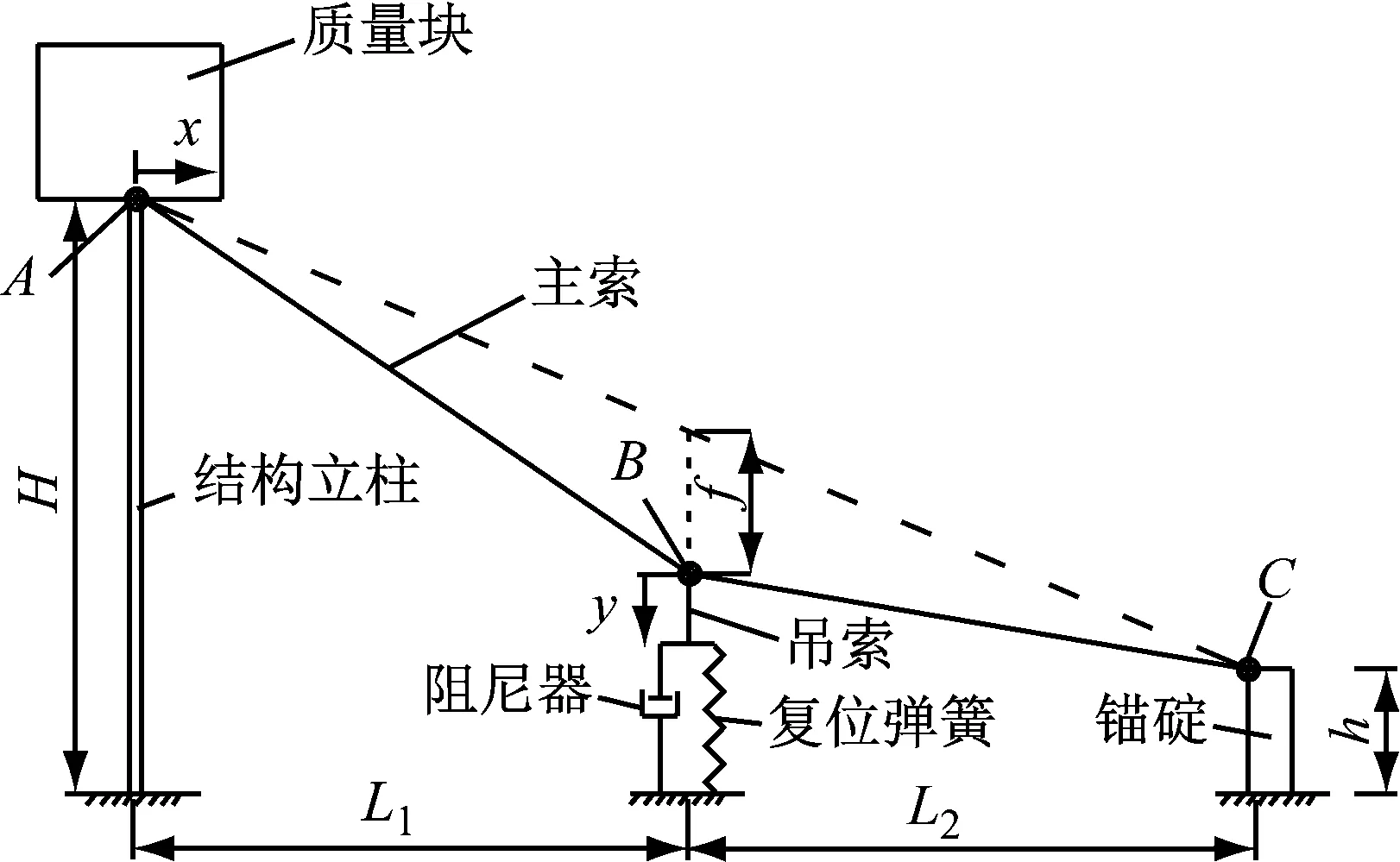
圖1 垂度阻尼索減振原理圖Fig.1 Structural vibration reduction theory with sag damping cables

1.2 垂度阻尼索對結構減振的振動方程

由于阻尼索主索軸向剛度遠大于結構立柱抗彎剛度和復位彈簧剛度，忽略主索軸向變形及阻尼索所有構件的質量，并將阻尼器安裝于主索跨中，得到

β=L1/2f

(3)

系統動能

(4)

由于吊索豎向位移遠大于其水平位移，忽略吊索水平位移，得系統勢能

(5)

阻尼力做功

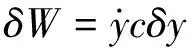
(6)

將式(3)～式(6)代入拉格朗日方程

(7)

得到該系統的振動微分方程

(8)

式中：m為質量塊的質量；x，y如圖1所示；k1為結構立柱抗彎剛度；k2為復位彈簧剛度，c見式(9)。

2 電渦流阻尼器力學性能試驗

2.1 電渦流阻尼器及測力裝置

電渦流阻尼器結構如圖2(a)所示，電渦流阻尼器由外紫銅管和內不銹鋼桿組成，在不銹鋼桿上安裝釹鐵硼超強磁鐵。銅管內徑35 mm，壁厚5 mm，長度500 mm；環形磁鐵片外徑30 mm，內徑10 mm，厚度5 mm。不銹鋼桿帶動磁鐵在銅管內移動時，銅管切割磁力線產生感應電渦流，電渦流又會產生一個與外部磁場相反的磁場，阻礙導體板與磁體之間的相對運動，這個力即電渦流阻尼力。

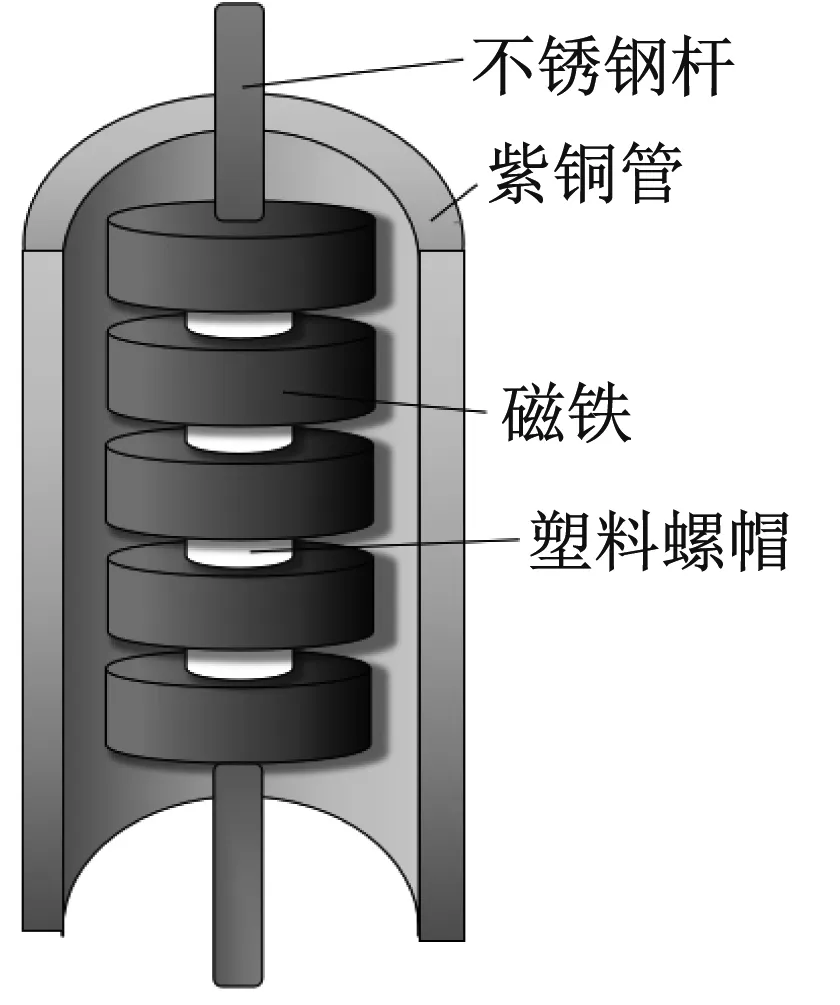
(a) 電渦流阻尼器

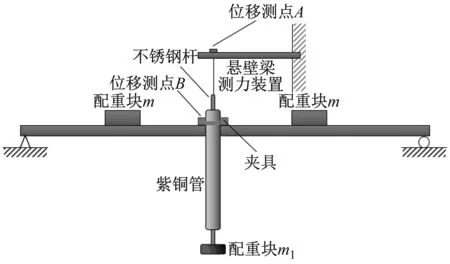
(b) 測力試驗裝置

電渦流阻尼力的測定裝置如圖2(b)所示。由兩端簡支的槽鋼、配重砝碼制作成振動系統，銅管固定于振動系統作豎向振動，不銹鋼桿-磁鐵組合體穿過銅管，上端用細繩與懸臂梁相連接，下端安裝配重阻止組合體隨電渦流作用力上下運動。當銅管相對于磁鐵上下運動時，電渦流阻尼力改變懸臂梁內彎矩，通過懸臂梁上黏貼的應變片可測量阻尼力的細微變化，同時采用激光位移計測量銅管(槽鋼)豎向振動的位移。

電渦流阻尼力是一種理想的黏性阻尼力[12]，阻尼力可表示為

F=cv

(9)

式中：c為黏性阻尼系數。磁鐵與銅管的相對運動速度v為

v(t)=(y(t+dt))-y(t-dt))/(2dt)

(10)

式中：銅管的豎向位移為y；dt為采樣時間間隔。

2.2 電渦流阻尼力測試結果

采用2片磁鐵為一組，試驗測量了采用一組至五組磁鐵時的阻尼力和位移，其中采用四組磁鐵時，電渦流阻尼力時間曲線如圖3所示。由圖可知，電渦流阻尼力近似正弦曲線，通過懸臂梁測得的阻尼力與由式(9)采用速度擬合的阻尼力值存在相位差，五種不同磁鐵組數的時差都為0.004 s。懸臂梁測力系統本身可視為一個有阻尼的振動系統，實測力為系統的輸出，電渦流作用力為系統的輸入，阻尼導致了時差的產生。

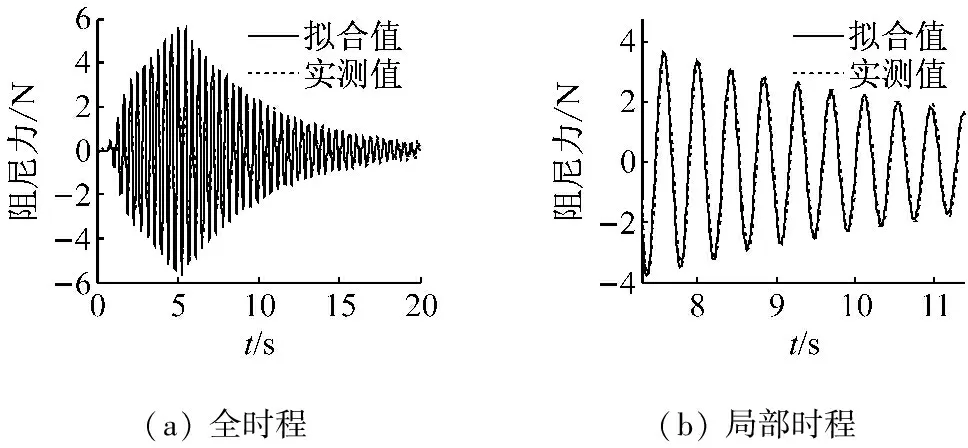
(a) 全時程(b) 局部時程

圖3 電渦流阻尼力時程曲線
Fig.3 The eddy current damping force-history curve

修正時差后實測阻尼力與式(9)擬合的阻尼力的時間曲線如圖4所示。由圖可知實測阻尼力與式(9)擬合的阻尼力吻合，由此可得到黏性阻尼系數c。

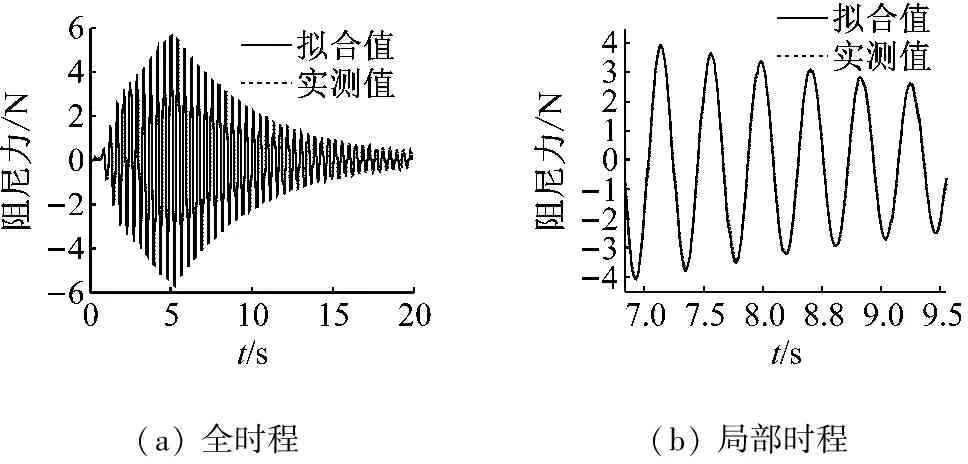
(a) 全時程(b) 局部時程

圖4 忽略時差影響的電渦流阻尼力時程曲線
Fig.4 The eddy current damping force-history curve ignored the time difference

電渦流阻尼力與銅管位移、速度的滯回曲線如圖5所示，阻尼力與速度成正例，可知電渦流阻尼器為理想的黏性阻尼器。

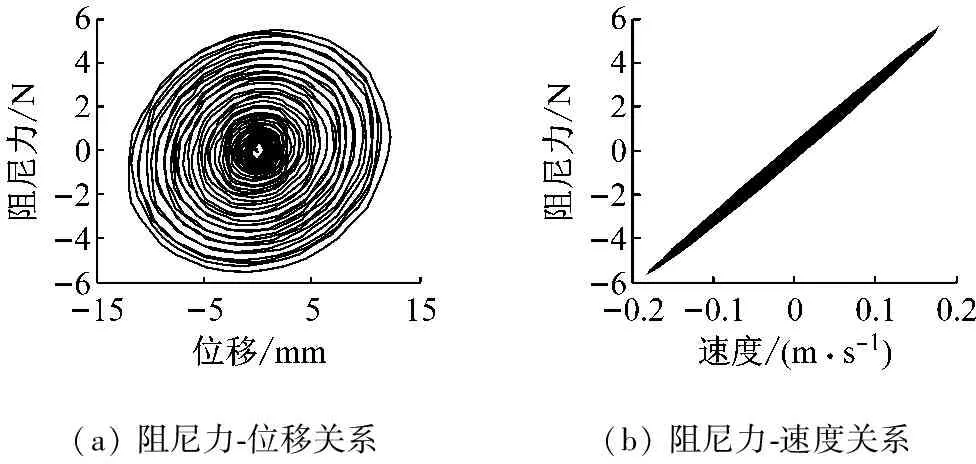
(a) 阻尼力-位移關系(b) 阻尼力-速度關系

圖5 電渦流阻尼力滯回曲線
Fig.5 The eddy current damping force hysteresis curve

電渦流阻尼器阻尼力黏性系數與磁鐵組數關系如圖6所示。僅安裝一組磁鐵時，c=6.8 N·s/m，多組磁鐵時，電渦流阻尼器黏性阻尼系數與磁鐵組數成正比。

c=8n

(11)

式中：n為磁鐵組數目，n=2，3，4，5。

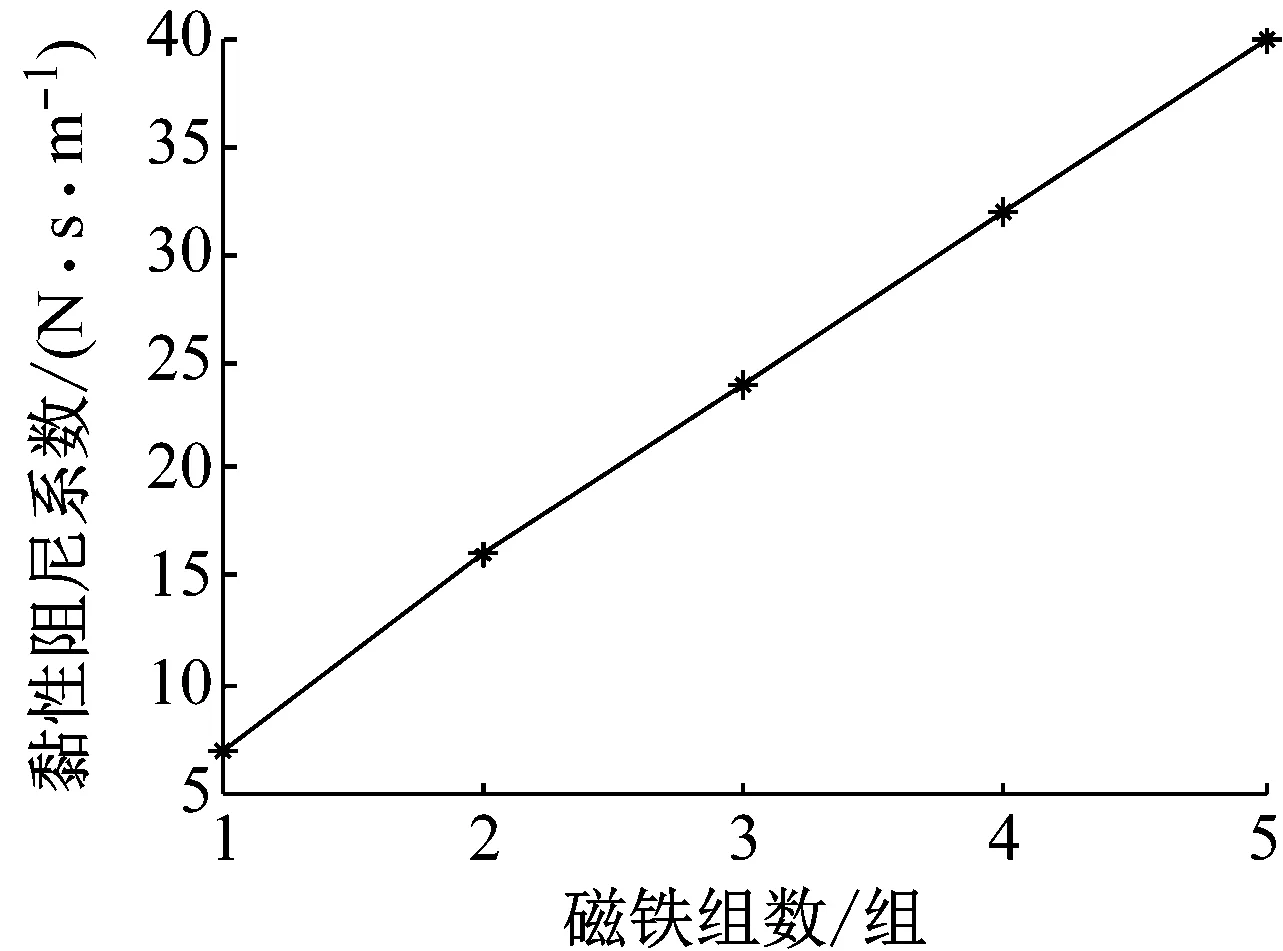
圖6 電渦流阻尼器黏性阻尼系數與磁鐵組數關系Fig.6 The relationship between the viscous damping coefficient and the number of magnets

3 垂度阻尼索減振試驗方法

3.1 試驗概況

垂度阻尼索結構減振試驗如圖7(a)所示，結構立柱橫截面采用長×寬×厚為60 mm×40 mm×4 mm的矩形鋼管，底端固定，在頂端安裝160 kg砝碼作為配重，頂部掛籃底至固定端3.0 m。主索一端固定于主結構掛籃底部，另一端錨固于地面錨碇，主索跨度16.8 m。在主索跨中安裝電渦流阻尼器和復位彈簧，彈簧與懸臂梁垂直連接，如圖7(b)所示。結構-阻尼索減振試驗基本參數如表1所示。

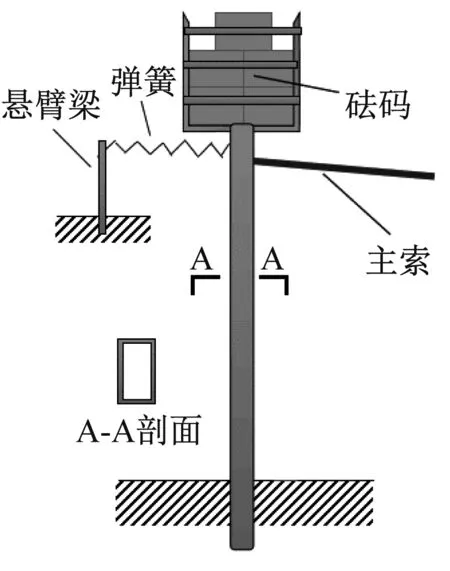
(a) 振動結構

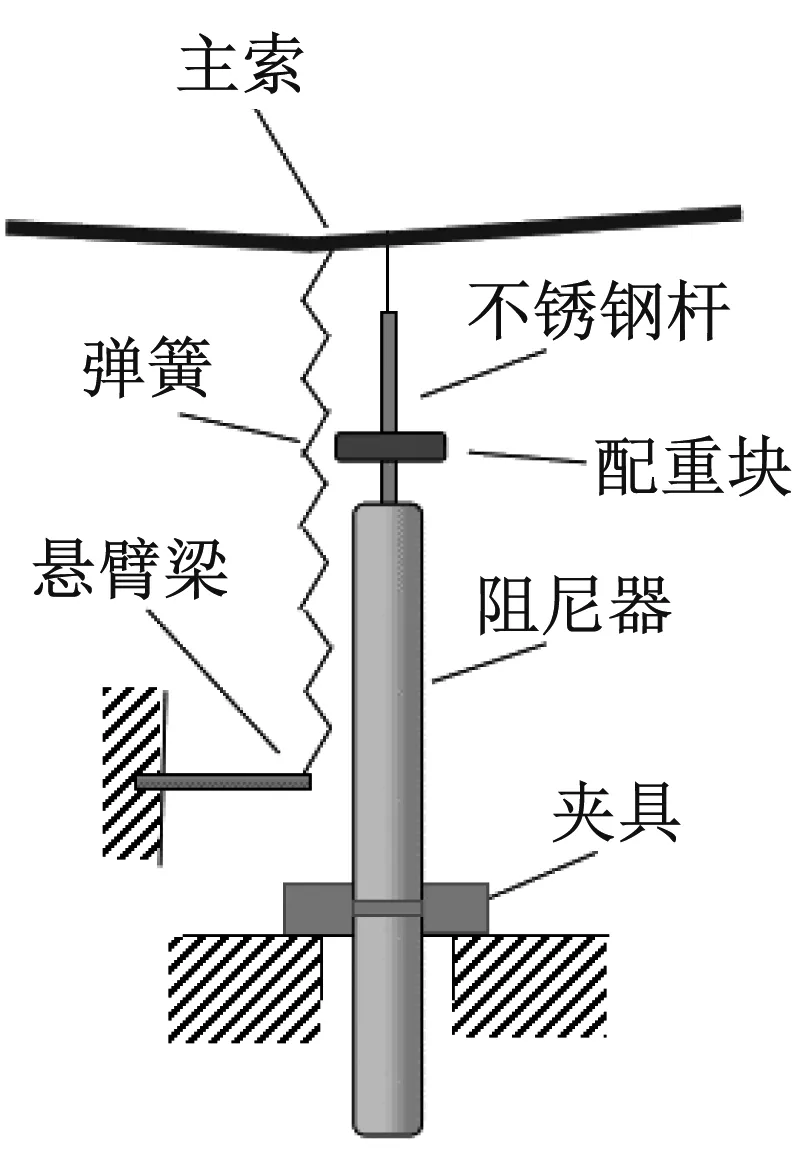
(b) 阻尼器及位移計安裝

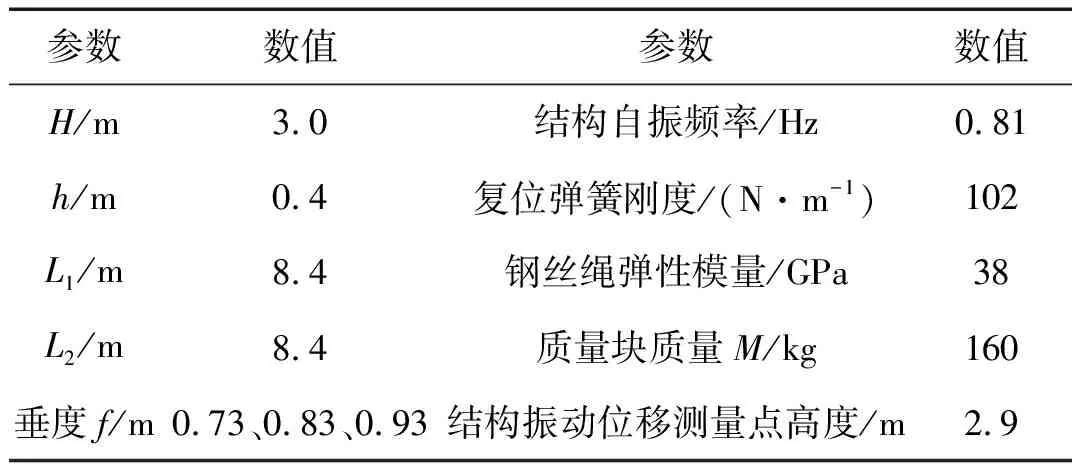
表1 試驗基本參數Tab.1 Basic parameters of experiment

由于阻尼器振動位移大，在懸臂梁上粘貼應變片，與彈簧共同形成位移傳感器，兩懸臂-彈簧式位移傳感器分別對結構頂部和主索跨中進行位移測量，如圖7所示。

3.2 試驗及阻尼比計算方法

采用人工激勵法使結構發生振動，當結構振幅達到設定值后突然撤除激勵，結構繼續發生自由振動。對結構振動位移進行數據采集，若采用包絡線法計算阻尼比，對于實測結構附加等效阻尼比較大，結構明顯振動僅數周的情形，可能存在較大的計算誤差，故本文采用結構一次衰減的振幅大于初始振幅0.1倍的前數周全部數據計算阻尼比

x=Ae-ζωntsin(ωdt)

(12)

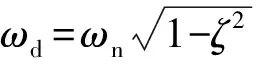
4 阻尼索減振試驗結果與分析

4.1 垂度阻尼索減振效果

為了對比垂度阻尼索的減振效果，首先對結構(無索、無阻尼器)、和結構+單索(無阻尼器)分別進行自由振動試驗，獲得的位移實測時程及式(12)擬合的時程如圖8所示，其等效阻尼比分別為：0.27%、0.36%，可見，未安裝阻尼器時結構體系的阻尼比很小，振動持續時間較長。

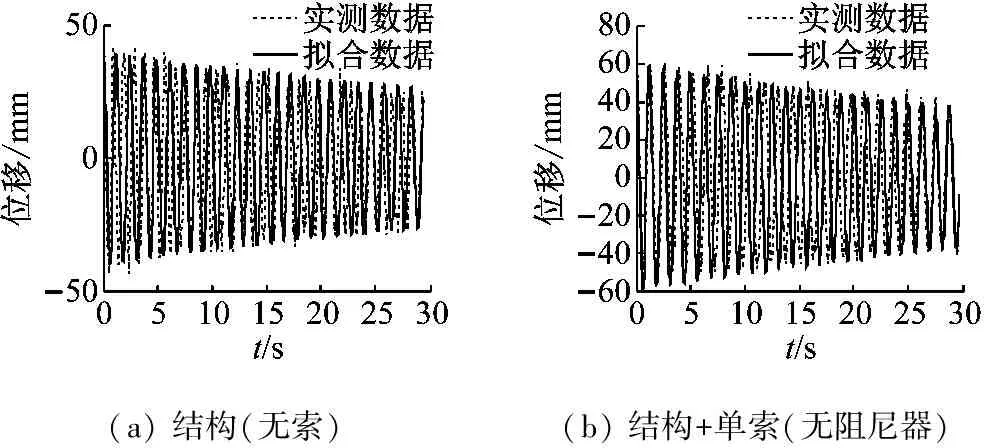
(a) 結構(無索)(b) 結構+單索(無阻尼器)

圖8 無阻尼器結構振動時程曲線
Fig.8 Time-history curve of structure vibration without damper

4.2 阻尼器阻尼系數對垂度阻尼索減振的影響

當主索垂度f=0.93 m時，結構在附加不同磁鐵組數的電渦流阻尼器的垂度阻尼索作用下，結構自由振動位移時程及式(12)擬合的時程如圖11所示。可見，安裝電渦流阻尼器后，振動周數快速減小，結構附加阻尼比顯著提高。

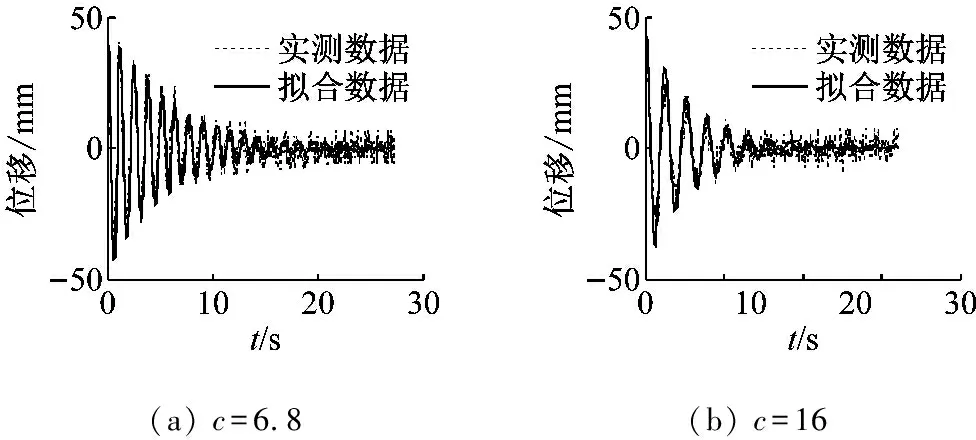
(a) c=6.8(b) c=16

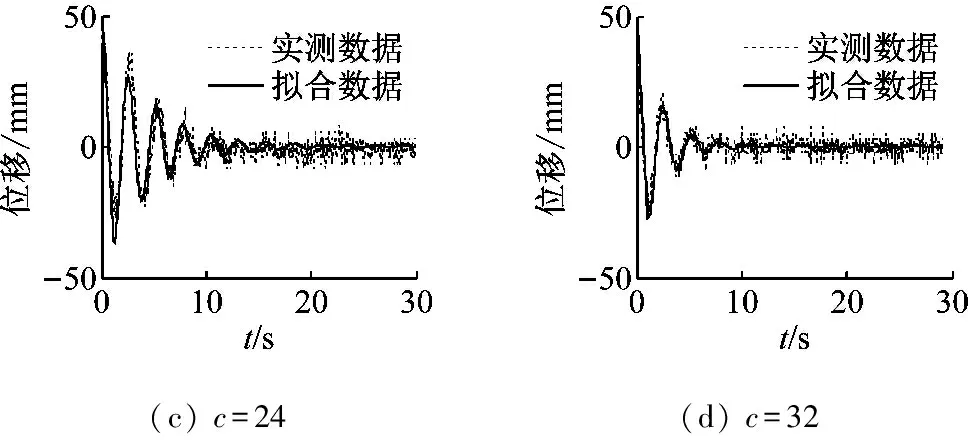
(c) c=24(d) c=32

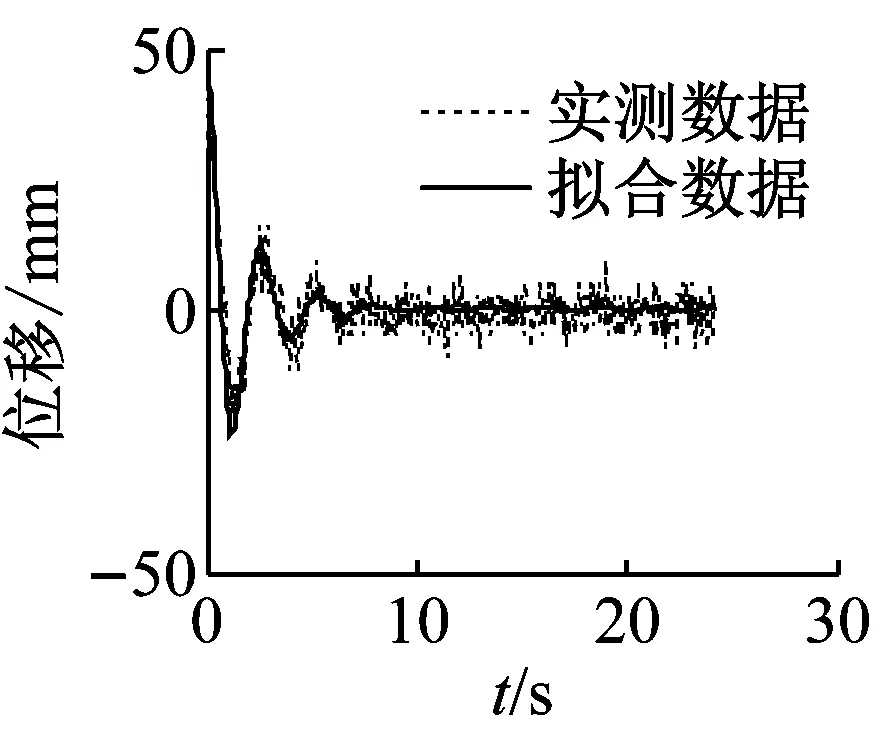
(e) c=40

改變主索垂度，重復上述試驗，采用式(12)計算結構附加等效阻尼比，不同垂度和不同阻尼器黏性系數下結構附加等效阻尼比如圖10所示，阻尼比數值如表2所示。

圖10 結構附加阻尼比實測值Fig.10 Measured values of additional damping ratio

由圖9、圖10及表2可知：① 垂度阻尼索對結構的減振效果明顯，最大附加阻尼比超過30%，隨著阻尼器黏性阻尼系數的增加，結構附加阻尼比加速增大；② 隨著主索垂度的減小，結構附加阻尼比增大。這是因為當垂度減小時，主索中點位移相對于主結構位移的放大系數隨垂度的減小而增大，在結構相同的振動位移下，增加了電渦流阻尼器的行程和速度，從而增加了垂度阻尼索的耗能能力。

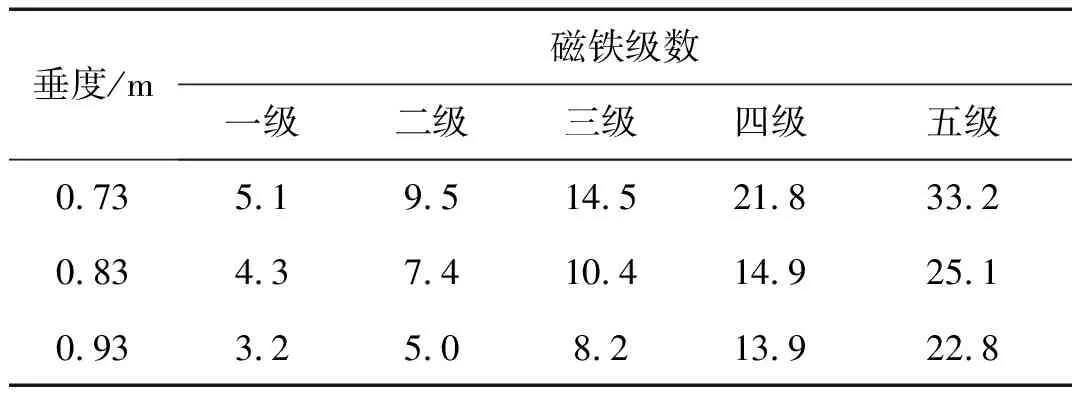
表2 實測結構附加阻尼比Tab.2 Measured additional damping ratio %

采用式(8)計算阻尼索主索不同垂度下的結構附加阻尼比如圖11所示，與圖10對比可知，實測阻尼比與理論解趨勢相同，但實測值較同條件下的理論解偏小，主要原因是理論解忽略了阻尼索的變形、位移放大系數的非線性影響。

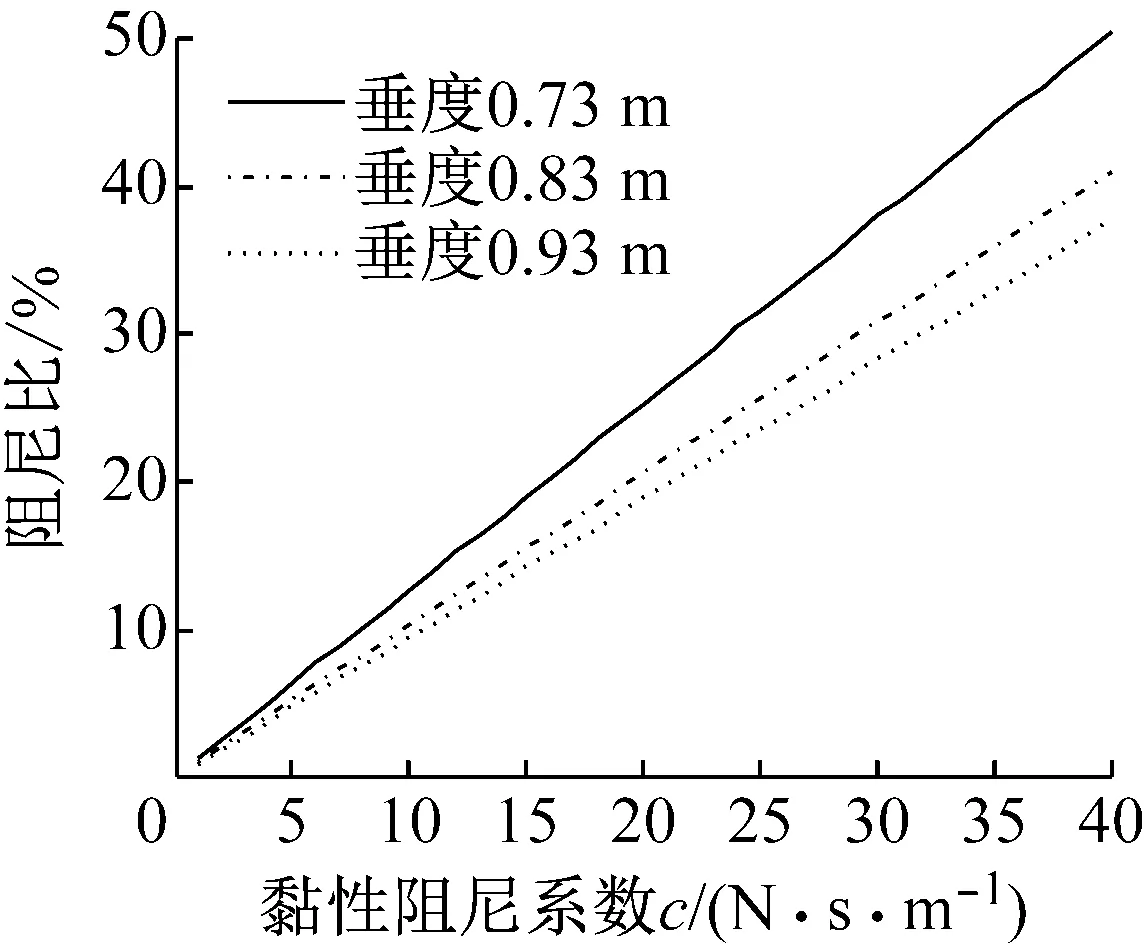
圖11 結構附加阻尼比理論值Fig.11 Theoretical values of additional damping ratio

5 結 論

本文進行了垂度阻尼索對高聳結構減振的模擬試驗，研究了阻尼索的垂度、阻尼器黏性阻尼系數對結構減振效果的影響，并對垂度阻尼索的結構設計及減振原理進行了分析，對電渦流阻尼器的設計及力學性能進行了研究，得到了以下結論：

(1) 垂度阻尼索能夠在高聳結構與地面長距離的兩位置之間安裝，利用結構與地面間的相對位移，通過主索放大后驅動阻尼器對結構進行耗能減振。

(2) 垂度阻尼索對結構減振的附加阻尼比隨阻尼器阻尼系數的增大而加速增大，對于試驗模型實測最大附加阻尼比已超過30%。

(3) 垂度阻尼索能充分利用結構振動的最大位移驅動阻尼器耗能，阻尼索本身結構簡單，實施方便快捷；并且阻尼索對結構的附加作用力較小，因此，垂度阻尼索可應用于工程實際高聳結構的減振，將結構的振動控制在很小的幅度內。