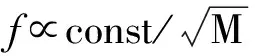非對稱類聲學超材料的低頻寬帶吸聲特性

牛嘉敏，吳九匯

(1.西安交通大學 理學院，西安 710049；2.西安交通大學 機械結構強度與振動國家重點實驗室，西安 710049)

劉正猷等[1]局域共振聲子結構的概念，拉開了聲子晶體的研究序幕。梅軍等[2-3]采用柔軟膜類和小質量塊的結構構建了一種薄膜型聲學超材料，在100～1 000 Hz有著良好的隔聲量。Naify等[4]提出的膜類聲學超材料，在100～1 000 Hz打破了隔聲質量定理的預測，而且可以通過調節共振質量塊的大小來改變隔聲量峰值。 Yang等[5]也得到了相似的聲學超材料，在不同的薄膜厚度和面密度下均有較好隔聲量。以上研究僅針對反射型膜類聲學超材料，并以隔聲量為衡量指標，但沒有考慮膜類聲學超材料的吸聲特性。梅軍等[6]提出了“暗”聲學超材料，通過在薄膜上鑲嵌新的金屬片，可在低頻區域100～1 000 Hz有效地吸收低頻聲波，從而展開了對吸收型膜類超材料的研究。Chen等[7]通過數值仿真和理論計算修正了吸收型膜類聲學超材料模型。吳九匯等[8-9]設計了新型螺旋局域共振單元聲學超材料，其在250 Hz以下的低頻范圍具有較寬的振動帶隙，最低帶隙頻率能夠低至42 Hz，但此聲學超材料的應用受重量的限制，而且在一些需要密封的場合不太適用。大量的理論和試驗研究都說明聲學超材料具有非常豐富的聲學特性，尤其膜類聲學超材料所具有的“負等效質量密度”，使薄膜材料在吸聲方面具有潛在的應用前景。而且薄膜材料具有便于清潔、防火、防銹蝕且可運用于惡劣環境等優勢，也可用于創造性的建筑結構設計中，易于裝配。

但在處理低頻問題時，膜類聲學超材料雖然有著良好的低頻特性，共振頻率的降低是以犧牲共振帶寬為代價的[10]，梅軍等提出的吸收型膜類聲學超材料在中頻段內有一個寬頻吸聲，但低頻段只有一個較窄的帶寬。怎樣在保證低頻吸聲特性的同時，讓結構也能具有一個寬頻的特性，是一個亟待解決的問題。本文在參考相關學者的基礎上，以非對稱吸收型膜類聲學超材料為研究對象，研究其非對稱性對整體吸聲性能的影響，并從膜類聲學超材料的等效質量密度和彈性應變能兩方面詳細探討其吸聲機理，找出非對稱性對吸聲系數的影響規律，以此設計了一種寬頻的吸聲結構，并通過數值計算得到低頻、寬頻的吸聲效果。

1 比較非對稱和對稱膜類聲學超材料的吸聲性能

參考梅軍等對于膜類(暗)聲學超材料結構的研究，采用有限元軟件COMSOL Multiphysics進行吸聲性能數值計算。本次數值仿真的結構單元為一塊厚度h=0.2 mm、長Lx=31 mm、寬Ly=15 mm的硅膠薄膜：密度ρ1=980 kg/m3、泊松比μ=0.48、楊氏模量E=1.9×106+iω(7.89×102) Pa，其中實部E1為薄膜的儲能模量，它與儲存在薄膜中的彈性勢能有關，虛部E2為損耗模量，與耗散在材料中的能量有關，該彈性模量可以表示為復模量的形式

E(iω)=E1(ω)+iE2(ω)=E1(ω)(1+iβ(ω))

(1)

其中β(ω)=4.2×10-4s。附著在薄膜表面的兩塊半圓鐵片，四周為固定約束，上下兩側均定義為空氣介質：ρ2=1.225 kg/m3，c=340 m/s。薄膜的初始預應力為σx=σy=2.2×105Pa。該結構吸聲系數的數值計算結果如圖1的黑色曲線所示。這和Chen等仿真的結果是一致的，校驗了數值計算的準確性。從圖1(a)可知，該結構第一個吸聲峰值頻率a處對應的振型為質量塊帶動薄膜的上下振動，大量的能量消耗在質量塊的外邊緣處，第二個吸聲峰值頻率b對應的振型為質量塊的扭振，第三個峰值頻率d對應中間薄膜的振動，能量消耗在質量塊的內邊緣和固定邊界處。三個共振模態的存在導致了該類型吸聲材料擁有著良好的低頻吸聲特性，但可以看出僅在峰值頻率處才存在著良好吸聲性能，其他頻率會出現低谷，導致噪聲很難完全吸收。在此基礎上開展非對稱膜類聲學超材料的寬頻吸聲性能研究。

對稱結構的吸聲帶寬較窄，針對該類型的膜類聲學超材料，重新分布兩個共振塊的質量。如圖1(c)的單元結構f所示，其中一塊質量塊密度為鐵片密度ρⅠ=7 870 kg/m3，另一塊鎂合金的密度ρⅡ=1 000 kg/m3。在COMSOL吸聲系數模塊下其計算結果如圖1所示。圖1(c)中：a，b，c，d，e分別代表每一吸聲峰值頻率處的振動模式。

(a) 對稱結構的振型圖

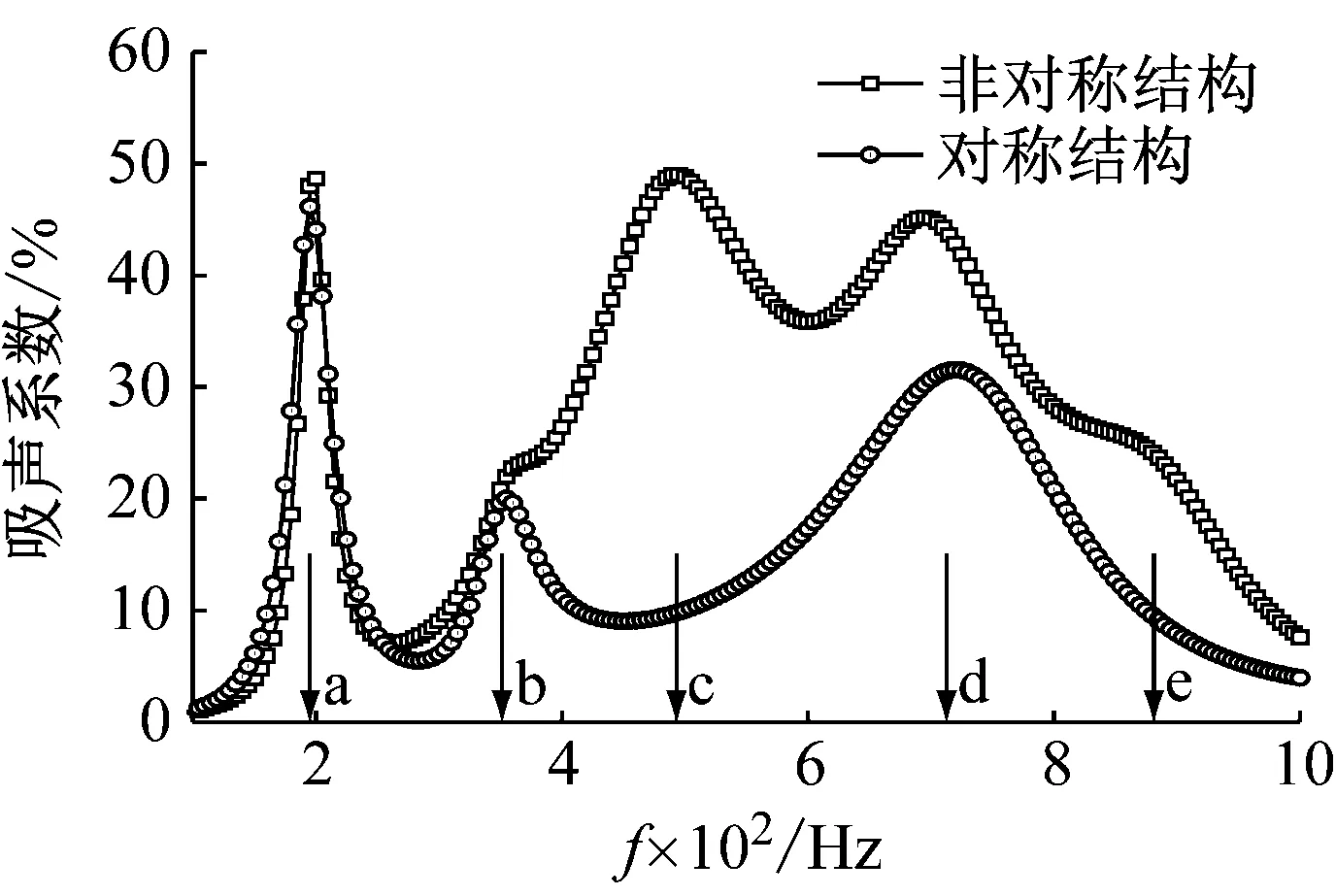
(b) 兩種結構吸聲系數對比圖

(c) 非對稱結構振型圖

從圖1(b)可知，對于對稱結構，在頻率的激勵下只能產生左右相互對稱的振型，吸聲峰值僅對應于a,b,d三個頻率處；而對于非對稱結構來說，其整體吸聲性能相比對稱機構來說整體提高了。本次仿真中，采取模型為在原來基礎上，改變其左右兩塊質量塊的對稱性而得。可以看出，非對稱結構的整體吸聲性能相比于對稱結構來說整體提高了，在保留對稱結構中頻率a,b和d對應的吸聲性能外，還增加了頻率c和e對應的吸聲峰值。從相應的振型可以看出，d模式對應的吸聲系數主要是由中間薄膜的振動引起的，只和膜振動的面積大小有關，因此對稱和不對稱結構在這個頻率處非常相似，而此時非對稱結構的峰值高于對稱結構是因為前者在振動中還夾雜了質量塊Ⅱ的Z方向振動，吸收了部分聲能。頻率a和b對應質量塊Ⅰ的Z向振動和扭振；頻率c和e對應質量塊Ⅱ的Z向振動和扭振。在非對稱模式下，結構整體的吸聲性能得到了極大的提高，吸聲帶寬從原來的窄頻帶擴大為寬頻帶。

2 非對稱膜類聲學超材料的吸聲原理

2.1 非對稱超材料的等效質量密度

首先來看該膜類聲學超材料的等效質量密度。對于該類型的膜類聲學超材料，可以等效為簡單的彈簧振子系統，其等效質量可以表示為

(2)

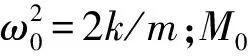
整個薄膜質量塊系統的有效質量密度ρeff可以通過COMSOL計算出來，根據文獻[2]有效質量密度定義為整個薄膜和質量塊系統的平均壓力除以整個域的平均加速度(兩者都是Z方向的)。從圖2可知，在非對稱結構的第一個吸聲峰值處，其有效質量密度為零，這時當結構受力時，必然會產生一個很大的加速度，此時薄膜質量塊處于共振狀態，邊界處的彈性應變能比較大，能量的耗散必然也大，因此會出現吸聲峰值。在第一個峰值右邊，出現了有效質量密度由正無窮大突變為負無窮大的情況，從動力學的響應來說，一個質量為無窮大的物體在一個力的作用下，其加速度必然無限趨近于零，此時結構本身在諧振子的作用下會產生一個相反方向的作用力，最終使得結構基本保持靜止，彈性能較小，所以吸聲峰值必然很低。可以看出，等效質量密度曲線每次經過零點的頻率(共有5個零點頻率)都對應于吸聲系數的峰值(共有5個峰值)。

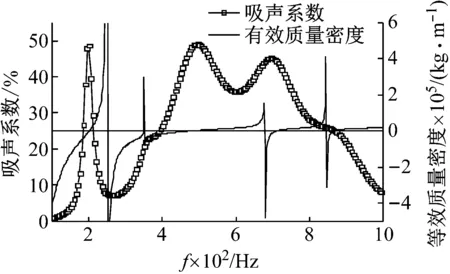
圖2 非對稱結構的等效質量密度Fig.2 Equivalent mass density of the asymmetric structure

2.2 非對稱超材料的彈性應變能

從應變能的角度來進一步探討該非對稱結構聲學超材料的能量耗散過程。根據薄板彎曲的直線法假設，平面薄板彎曲時的應變能為

Qε=1/2 ?(σxεx+σyεy+τxyγxy)dxdydz

(3)

考慮到薄膜是一種柔性材料，在外力下會產生有限的變形，此時薄膜的位移分量和其偏導數不能忽略，可以采用拉格朗日法來具體描述物體的變形問題[11]，相應的應變位移關系和應力應變如式(4)和式(5)所示，其中εz=γyz=γxz=0。

(4)

(5)

根據薄板彎曲的應變能表達式Qε，并將坐標z從-h/2到h/2進行積分可以得到

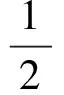
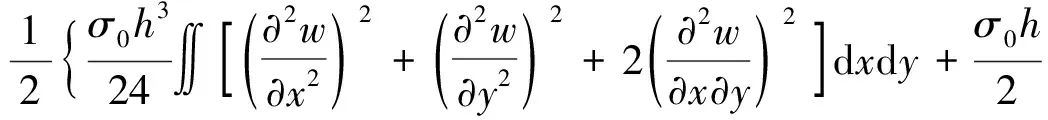
(6)

對于四周固定的矩形薄板，利用斯托克斯公式推導可以得到

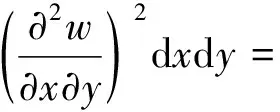
(7)

將式(7)代入式(6)，即得

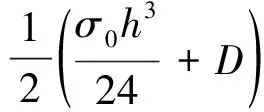
(8)

從式(8)可知，在預應力的作用下，薄膜的等效彎曲剛度調整為

(9)

梅軍等指出，該膜類聲學超材料的w一階導數在鐵片邊界處不連續，從而導致了在這些邊界處Qε的數值會很大，彈性薄膜的耗散能量與薄膜整體的彈性應變能成正比，因此在每一處彈性應變能峰值處都對應吸聲系數的峰值，從圖3可知，非對稱結構的吸聲系數峰值頻率和彈性應變能的峰值頻率一一對應。利用COMSOL軟件可以直接提取計算結果中薄膜質量塊系統的整體彈性應變能，如圖3所示。相較于對稱結構來說，非對稱相對對稱聲學超材料結構的彈性應變能整體數值<340 Hz時它們基本吻合，在>340 Hz時有較大地提高。

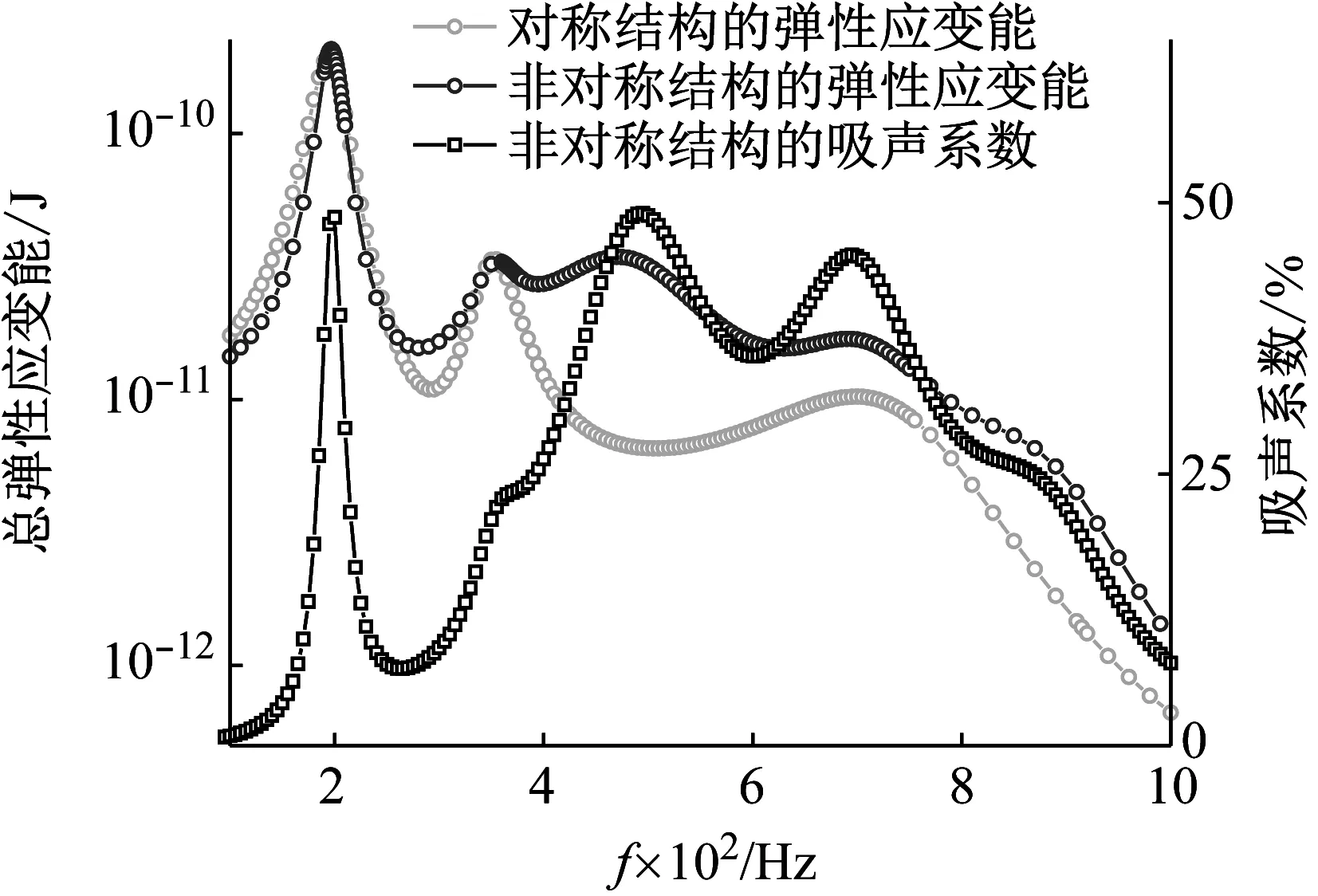
圖3 非對稱結構的彈性應變能和吸聲曲線Fig.3 Elastic strain energy and absorption curve of asymmetric structure

由圖3可知，圖示兩種結構的第一個峰值和第二個峰值，不管是應變能的幅值還是峰值頻率，它們的差異都非常小，即對稱結構和非對稱結構在這兩個頻率處的總彈性應變能是基本相同的，從上一節也可以看出雖然兩者前兩階振型不一樣，但也依舊具有相同的吸聲系數，也說明了前兩個吸聲峰值主要受質量塊Ⅰ的調控，另一方面，從對稱結構的一階振型可以看出雖然兩質量塊都在振動，但由于振動的對稱性也帶動了中間薄膜跟隨運動，應變能大部分分布在半圓鐵片的外邊緣，內邊緣基本沒有應變，而非對稱結構雖然只有質量塊Ⅰ在振動，質量塊Ⅱ卻基本靜止，此時大部分的應變能就分布在質量塊Ⅰ的外邊緣與內邊緣處，因此對稱結構和非對稱結構在此頻率處具有相似的應變能和吸聲系數；隨著頻率的升高，質量塊Ⅱ在聲波的激勵下達到其共振頻率，在第3個峰值頻率處產生了較大的應變能，因此吸聲系數也在這個頻率處達到了峰值，同樣第5個應變能峰值也對應著質量塊Ⅱ的扭振；第4個峰值處，對稱結構和非對稱結構在峰值頻率上相差不大，只是幅值產生了變化，非對稱結構的應變能峰值大于對稱結構的，這從振型圖中也可以解釋，振型d在對稱結構下只是中間膜的振動，相應的應變能集中在質量塊的內邊緣，在非對稱結構下振型即包括中間薄膜的振動，也包括質量塊Ⅱ的伴隨振動，應變能除了分布在兩質量塊的內邊緣之外，也分布在質量塊Ⅱ的外邊緣，因此在此頻率處，非對稱結構的整體應變能是高于對稱結構的。整體來說在非對稱模式的影響下，結構的總彈性應變能在全頻段內高于對稱模式的應變能，這也吸聲系數差異比較明顯的原因之一。

3 非對稱性聲學超結構的寬頻吸聲影響規律

3.1 膜類聲學超材料非對稱性的影響規律

研究膜類聲學超材料左右不對稱的程度對其吸聲系數的影響規律，先定義一個變量密度比例因子μ=ρ2/ρ1，其中ρ1為第一塊即左邊質量塊，ρ2為第二塊即右邊質量塊密度。在COMSOL軟件中可以計算出，隨著密度比μ的改變吸聲系數的變化趨勢，如圖4所示。選取了具有代表性的μ=0.1，0.3，0.5和1.5作為參考。可以看出，隨著密度比的改變，其中有三個峰值頻率處是不改變的，分別是對稱結構下的三個峰值頻率處a，b和d，這說明前兩個峰值主要受第一塊質量塊調節；其余兩個峰值頻率隨著密度比改變而改變，并表現為一定的規律，如圖5所示。質量塊Ⅱ的一階和二階峰值頻率擬合后基本呈現式(10)的規律。

(10)

式中：M為第二塊質量塊的質量；這也說明了這兩個峰值主要受第二塊質量塊的調節。我們可以通過適當地調節不對稱比例來達到相應的低頻、寬頻要求。

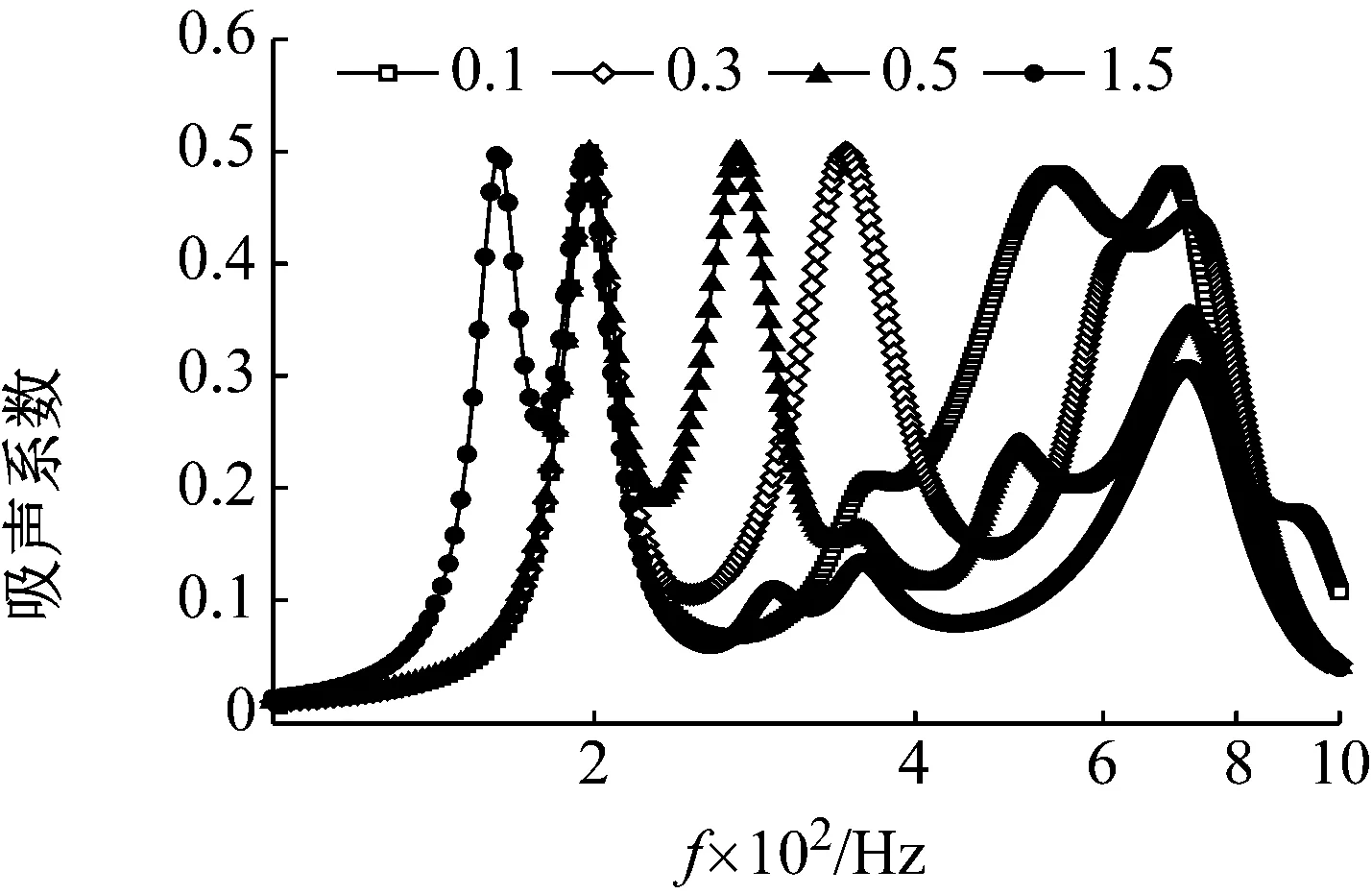
圖4 密度比μ改變對吸聲系數的影響Fig.4 The influence of density ratio μ change on the sound absorption coefficient

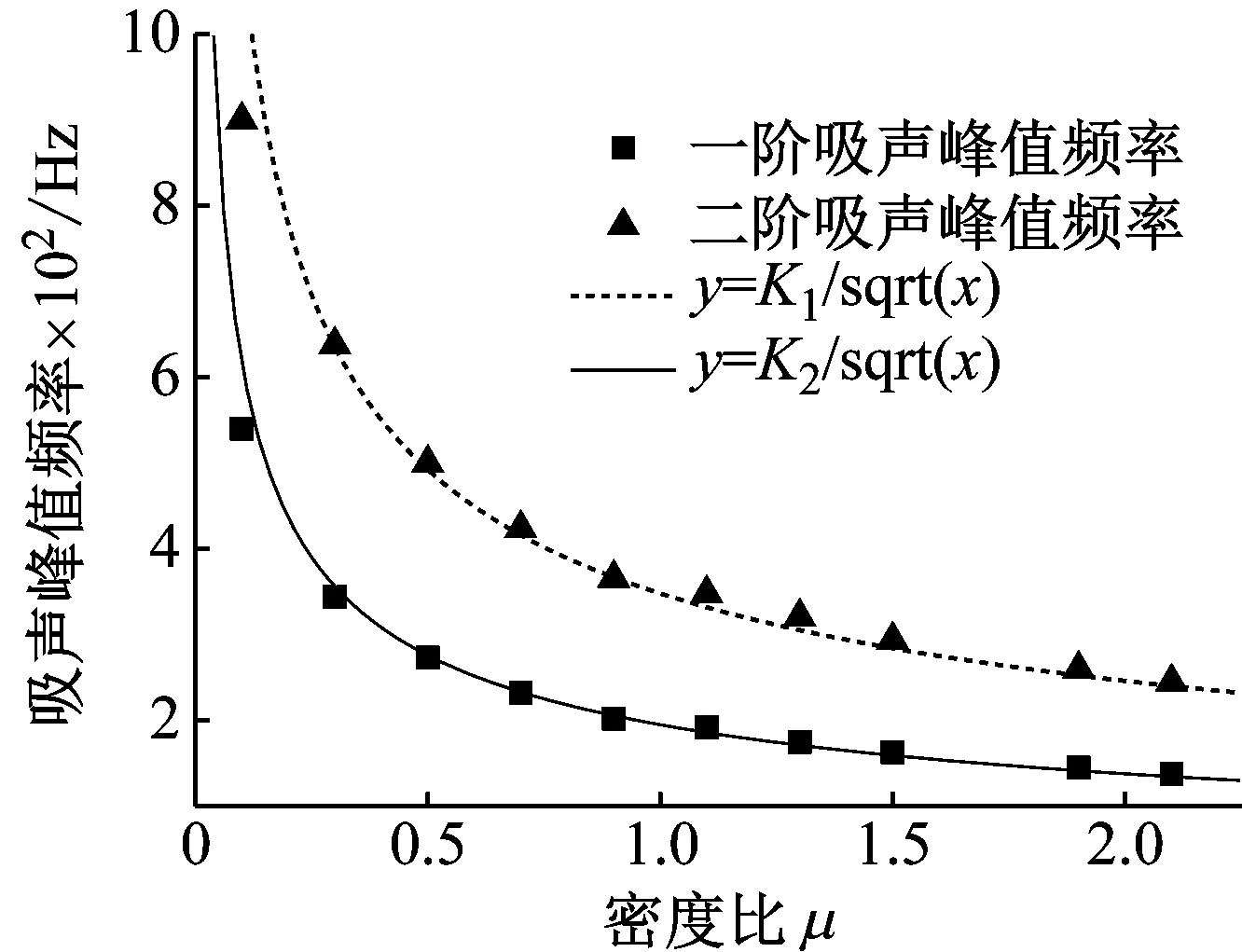
圖5 一、二階峰值頻率隨密度比μ的變化規律Fig.5 First and second order peak frequency changing with the density ratio μ

非對稱性對于膜類聲學超材料的吸聲系數有著比較大的提高，但在實踐中密度比μ的改變很難實現。質量m=ρV，我們可以通過質量塊的厚度改變質量塊體積，從而達到改變質量的目的，圖6所示為質量塊Ⅱ的一、二階吸聲峰值隨厚度比γ的變化規律，和圖5的密度比改變具有相似的變化趨勢，通過調節質量塊厚度可以實現整體吸聲系數的調節。

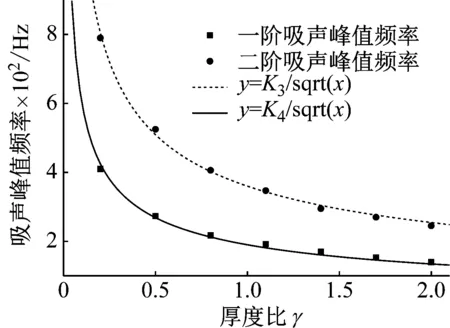
圖6 質量塊Ⅱ的一階和二階峰值頻率隨厚度比μ的變化規律Fig.6 First and second order peak frequency of mass block Ⅱ changing with the thickness ratio μ

3.2 非對稱型超材料的低頻寬帶吸聲

根據上一節質量塊Ⅱ的一階和二階峰值頻率隨密度比μ的變化規律，我們設計了以下的結構，如圖7所示。該結構由四個相同大小的單元組成，每個單元有兩個不同的質量塊，其中ρⅠ=7 870 kg/m3；ρⅡ=7 000 kg/m3；ρⅢ=6 000 kg/m3；ρⅣ=5 000 kg/m3；ρⅤ=4 000 kg/m3；ρⅥ=3 000 kg/m3；ρⅦ=2 000 kg/m3；ρⅧ=1 000 kg/m3。

圖7 寬頻吸聲結構示意圖Fig.7 The diagram of broadband acoustic structure

本次仿真中改變密度來實現寬頻吸聲，實驗中可以通過改變質量塊厚度來實現。模型中每個單元四周都采用固定約束的方式，營造一個完全封閉的系統，實際中采用絕對硬邊界，邊框及中間位置采用玻璃鋼等較硬材料實現，以保證質量塊共振時互不影響。

該類型寬頻結構的吸聲性能如圖8所示，并對比圖1的對稱結構吸聲性能。可以看出僅僅采用0.2 mm厚的薄膜和8塊質量互不相等不同材料的質量塊，就能實現用小尺寸結構達到低頻段的吸聲特性，根據物理結構，每個質量塊的不同頻率性質，實際中每個質量塊是并聯的。并且更重要的是在整個低頻段內(195～700 Hz)都具有一個很高的吸聲系數。即實現了低頻的需求，也解決了寬頻的難點問題，一舉兩得。該類型非對稱結構的聲學超材料利用其不對稱性造成的多個共振模式，從而拓寬了低頻段內的吸聲效果。

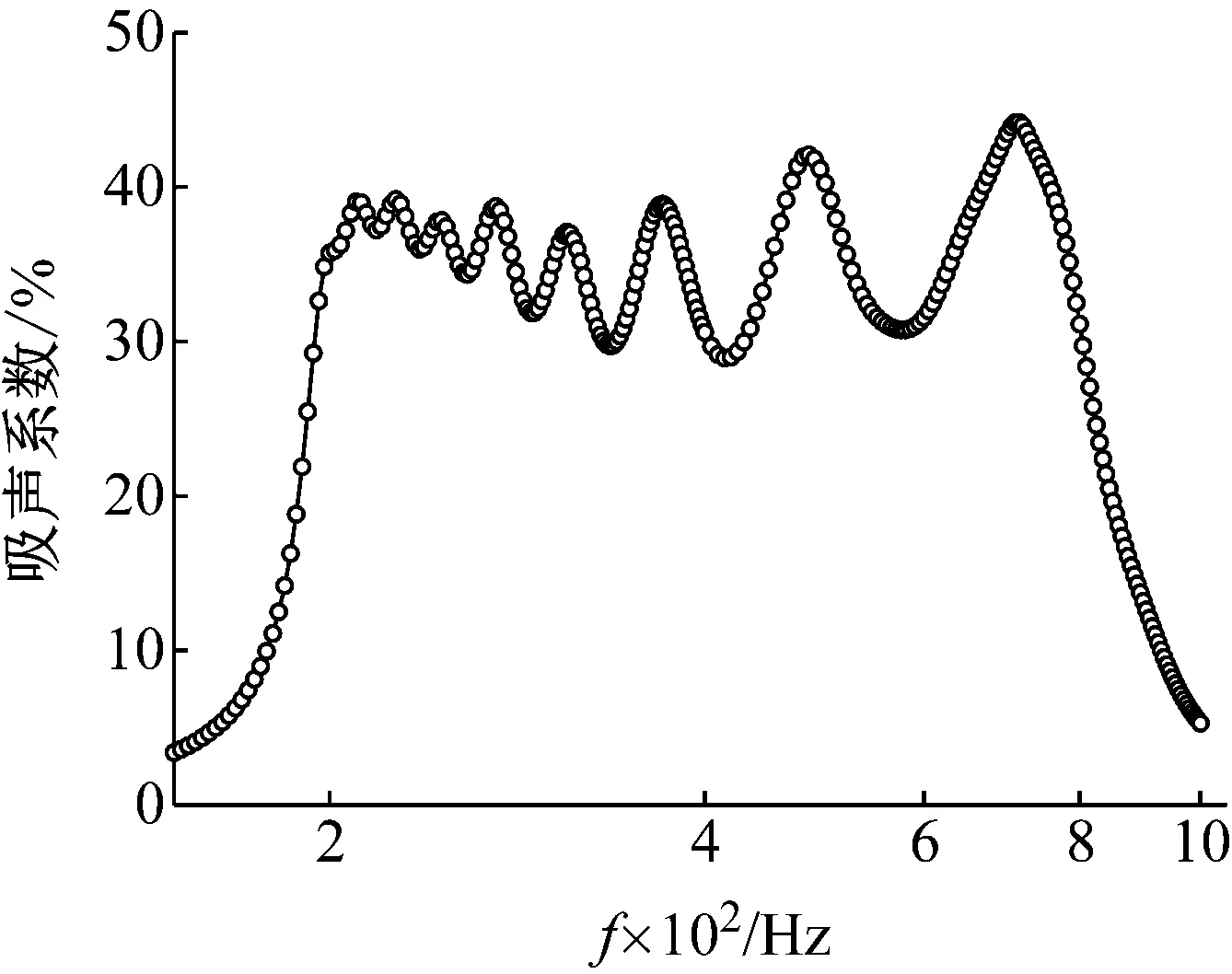
圖8 非對稱結構的寬頻吸聲性能Fig.8 The broadband sound absorption performance of asymmetric structure

4 結 論

在參考相關研究的基礎上，以吸收型膜類聲學超材料為研究對象，研究了共振質量塊的非對稱性對結構低頻、寬頻吸聲性能的影響，并得出了以下結論：

(1) 首先從通過COMSOL的聲固耦合模塊對非對稱聲學超材料進行了吸聲系數的數值計算，在非對稱模式下，結構整體的吸聲性能得到了極大的提高，吸聲帶寬從原來的窄頻擴大為寬頻。

(2) 針對非對稱聲學超材料，從等效質量密度和整體的彈性應變能兩方面分析了結構的吸聲原理。等效質量密度為無窮大的頻率點處對應吸聲系數的谷值，經過零點的頻率(共有5個零點頻率)都對應于吸聲系數的峰值；整體來說在非對稱模式的影響下，結構的總彈性應變能在全頻段內高于對稱模式的應變能。