隨機地震作用下剪力墻結構振動臺試驗研究
徐亞洲,劉克東,劉章軍,蘇寧粉
(1.西安建筑科技大學 土木工程學院,西安 710055;2.三峽大學 土木與建筑學院,湖北 宜昌 443002)
地震作用具有顯著的隨機性[1]。早在1947年Housner即將結構地震反應視為一種隨機振動,許多研究者針對隨機地震動開展了深入細致的研究[2]。迄今為止,結構隨機地震響應分析僅限于數值分析。柳偉等[3]基于概率密度演化理論研究了環形隔板對圓柱形罐體中液面晃動響應的影響。劉章軍等[4]應用非平穩地震動概率模型,對重力壩隨機地震反應和抗震可靠度進行了分析。但幾乎沒有土木建筑結構隨機試驗研究的報道。
剪力墻結構作為目前民用住宅中使用最為廣泛的一種結構形式,其抗震性能一直是研究者關注的重點。王維等[5]開展了預制剪力墻結構和預制剪力墻隔震結構的1/4縮尺模型振動臺試驗,比較了兩者的結構動力特性和地震反應,并研究了裝配式剪力墻水平接縫連接的可靠性。李書進等[6]對武漢世貿錦繡長江地段的某超高層住宅進行了1/30的縮尺模型振動臺試驗,研究了結構在6度多遇、6度設防、6度罕遇、7度罕遇地震作用下的動力反應。
但現有的剪力墻振動臺試驗研究均只按照規范要求選波開展確定性地震反應試驗研究,沒有考慮地震作用的隨機性。然而,眾所周知,地震動無論在時間、空間、強度和頻譜上都具有很強的隨機性。一條地震波僅可視為隨機過程的一次樣本實現,即使相同地點、同一結構也不可能遭受完全相同的兩次地震作用。
為了在振動臺試驗過程中考慮地震動的隨機性,本文在隨機過程正交展開理論[7-8]的基礎上,實現了采用基本隨機變量的函數形式來構造隨機地震動過程[9-10]。基于非平穩地震動概率模型和規范反應譜,利用基本隨機變量的離散代表點集,生成了適用于7度設防的34條非平穩多遇地震動樣本。同時,設計和制作了一個1/5縮尺的12層鋼筋混凝土剪力墻模型進行振動臺試驗研究[11],開展了結構隨機地震響應測試,基于試驗結果分析了主要響應量的均標、準差、變異系數,并估計了相應的概率密度函數。
1 模型設計及制作
1.1 模型簡介
原型結構為7度設防、Ⅱ類場地,設計地震分組為第一組,該類剪力墻結構的抗震等級為二級。根據試驗條件和目的,確定模型的幾何相似系數Sl為1/5,其他相似系數可由量綱分析法確定。綜合考慮原型結構的特點、振動臺設備條件以及模型材料制備等方面的因素,試驗最終采用的主要相似系數見表1。基于此,設計了一個相對規則的12層現澆剪力墻結構模型(僅包含一個標準層),模型平面布置如圖1所示。其中模型結構總高度為7.2 m,每層層高為0.6 m,平面尺寸為1.8 m×1.8 m。
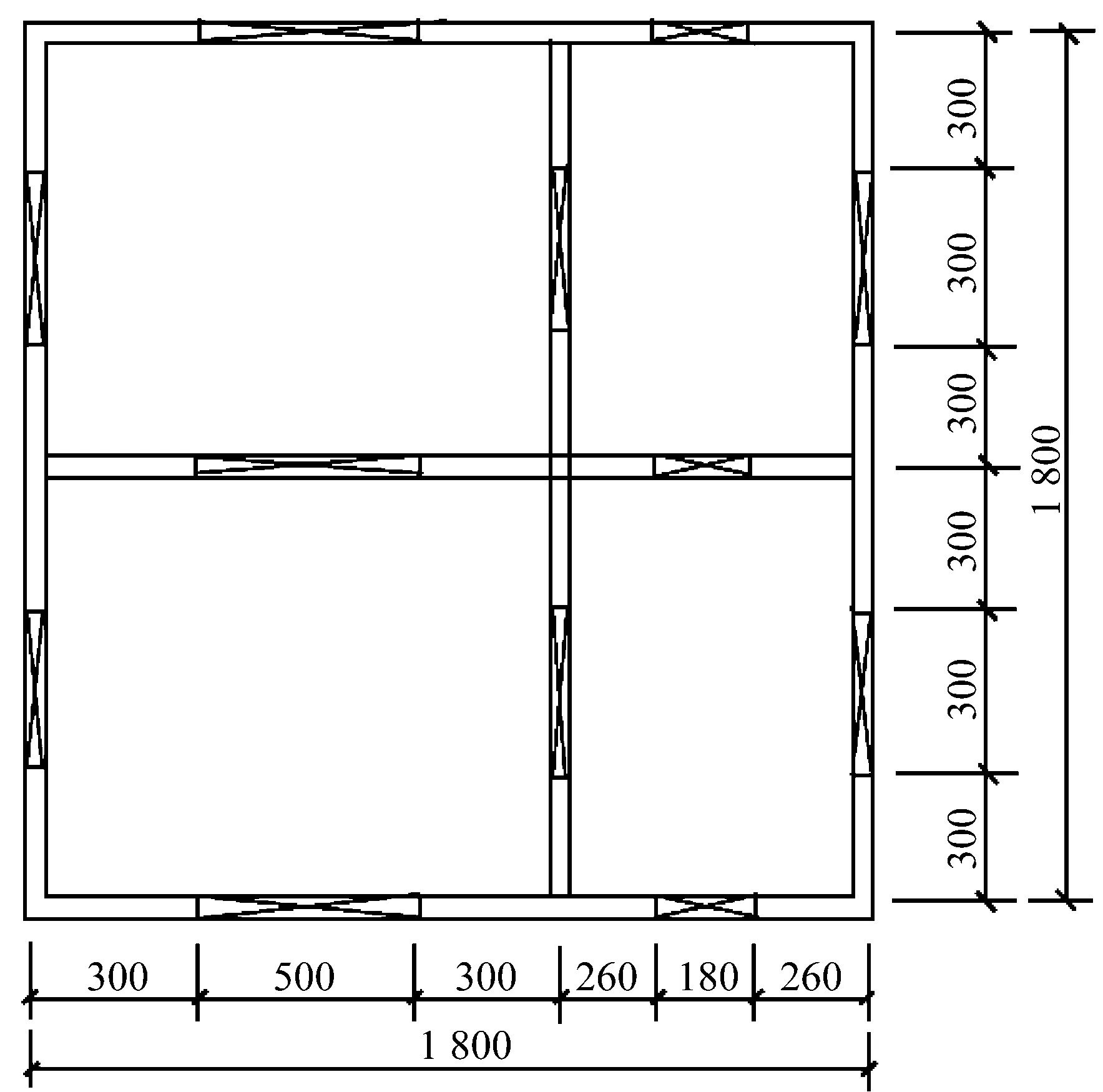
圖1 試驗模型建筑平面圖Fig.1 Plane layout of the model
模型制作完成后高度為7.55 m(包括底座),總質量13.36 t,其中模型結構與基礎底座的質量為11.8 t,附加質量為1.56 t。制作完成后的模型見圖2。

表1 模型主要相似關系Tab.1 Similarity constants of the model

圖2 剪力墻模型全貌Fig.2 Schematic of the shear wall model
1.2 模型材料
采用細石微粒混凝土來模擬原型結構中的C40混凝土,并用鍍鋅鐵絲來模擬鋼筋。經試配后最終確定微粒混凝土的配合比為,水泥∶石子∶沙子∶水∶石灰=1∶3.64∶3.64∶1.11∶0.5。實測所得微粒混凝土的彈性模量為E=7 030 MPa,立方體抗壓強度均值為fcu=8.94 MPa,質量密度為2 500 kg/m3。
2 試驗方案
2.1 測試方案
試驗主要測試模型的動力特性及34條隨機地震動作用下結構的加速度反應和位移反應。根據測試目標,分別在模型X向及Y向中軸線位置上沿地梁頂到12層頂每層布置加速度計和位移計來分別記錄模型結構的加速度和位移。
2.2 隨機地震動生成

(1)

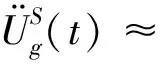
[cos(ωkt)Xk+sin(ωkt)Yk]
(2)
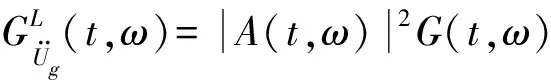
譜表示-隨機函數方法中,Xk與Yk為標準正交隨機變量,即:
E[Xk]=E[Yk]=0;E[XjYk]=0;
E[XjXk]=E[YjYk]=δjk
(3)
式中:E[·]表示數學期望;δjk為Kronecker記號。
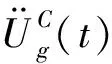
(4)
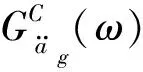
本文將基本隨機變量均勻離散為34個代表點集,由譜表示-隨機函數方法生成34條隨機地震動樣本。圖3為上述方法生成的一條代表性樣本時程,可以發現該樣本具有非平穩地震動加速度過程的典型特征。圖4為34條代表性樣本時程均值反應譜與目標反應譜(規范反應譜)的比較。可以發現,均值反應譜與目標反應譜吻合良好,平均誤差為6.23%。長周期部分(大于4.5 s)誤差稍大,但本模型結構的主要自振周期不在該范圍內。
2.3 加載方案
根據相似性原理,對地震波進行時間軸上的壓縮,則原始波經壓縮后的總時長為8.94 s,加速度幅值相似比為1。此外,為了測試模型結構的初始動力特性、了解不同階段結構的損傷發展狀況,在試驗之前以及每隔9條隨機波加載后對模型結構進行白噪聲掃頻,記錄和分析模型結構自振頻率、振型、和阻尼比等動力參數的變化,避免結構損傷累積過大,保證每條地震動樣本作用下結構的響應具有可比性。考慮白噪聲掃頻,隨機地震動試驗加載工況共計39個。
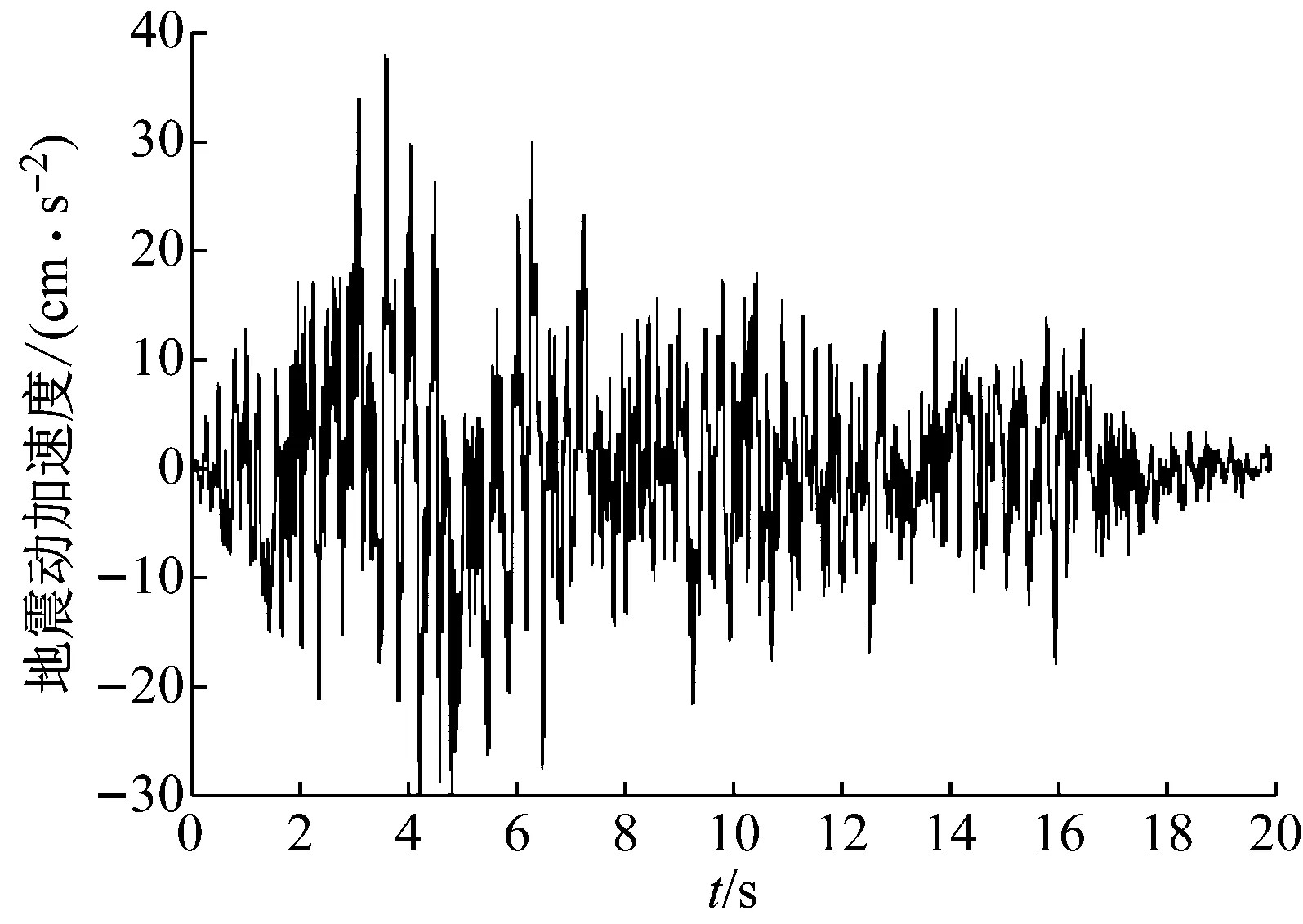
圖3 代表性地震動樣本時程Fig.3 Representative time history of ground motions
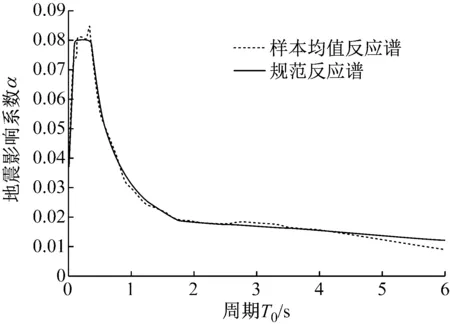
圖4 集合平均反應譜與規范反應譜的比較Fig.4 Comparison between the averaged response spectrum of 34 samples and the code’s response spectrum
3 試驗結果
3.1 結構動力特性
每隔9條隨機地震動試驗后,均用白噪聲對模型結構進行掃頻。通過對加速度測點頻譜特性、傳遞函數的分析,獲得了模型結構在隨機地震動加載前后的自振頻率、阻尼比和振型比較。由圖5可以發現五次掃頻所得前兩階振型基本重合,此即說明:施加34條隨機地震動前后結構的自振頻率未發生明顯變化,結構整體處于彈性狀態。此外,隨機地震動加載前后白噪聲掃頻測得的模型結構剛度和阻尼比也基本一致,如表2所示。
3.2 模型加速度反應
試驗模型在每條樣本地震波下的動力反應是本次試驗測試的主要目標之一,分析各層在樣本地震動作用下的加速度時程記錄,可以得到模型的隨機動力響應。圖6為典型隨機地震動作用下模型結構X方向頂部加速度時程和相對位移時程樣本。
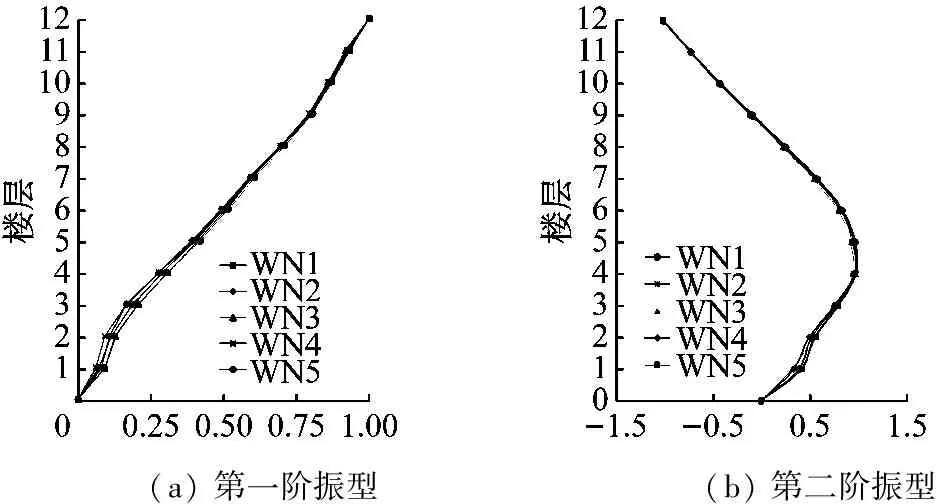
(a) 第一階振型(b) 第二階振型

表2 結構自振頻率、阻尼比Tab.2 Natural frequency and damping ratio

(a) 12層加速度時程
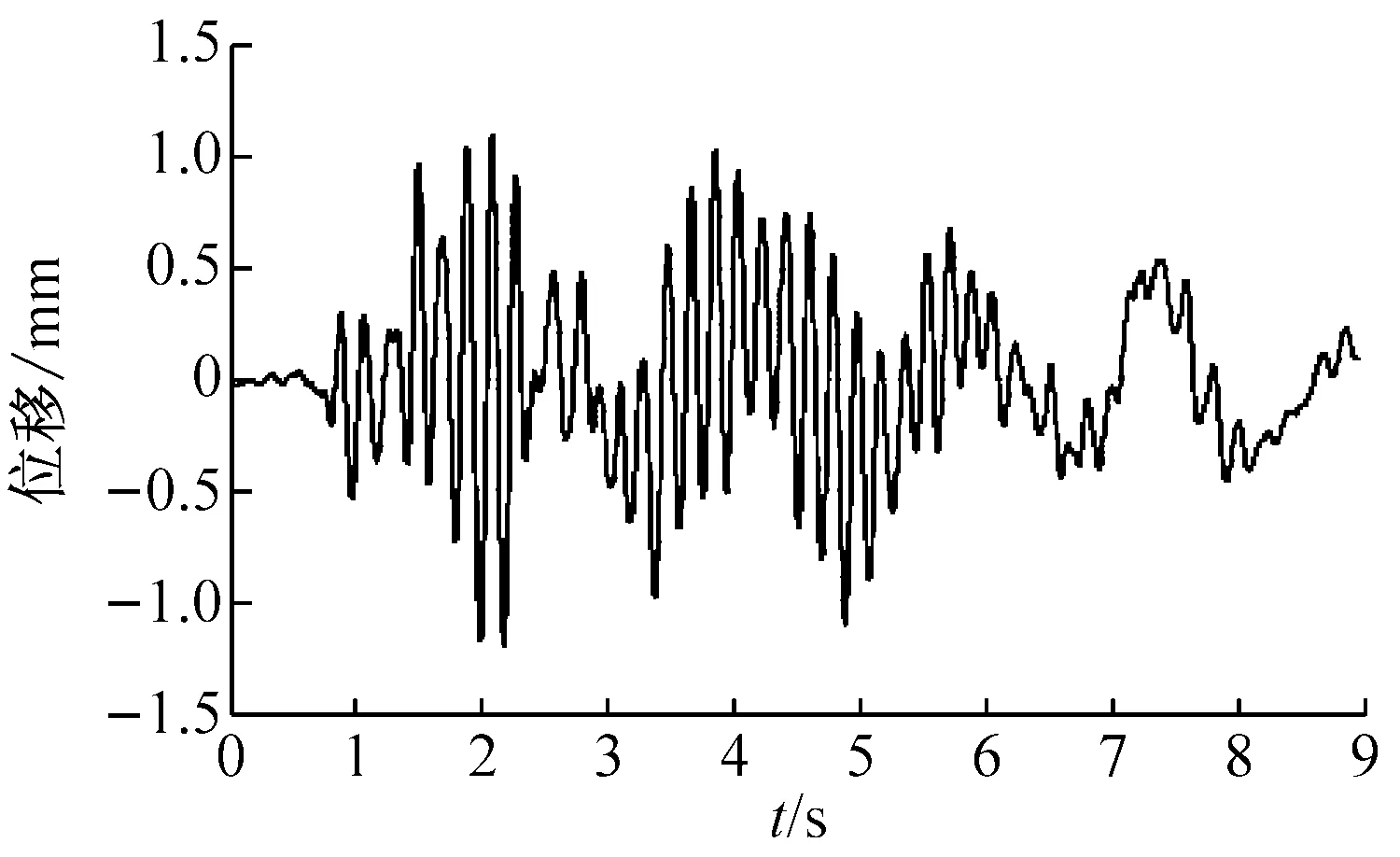
(b) 12層位移時程
以布置在地梁頂面加速度計實測的加速度最大值作為參考,將模型結構各層加速度響應在同一工況下的峰值與其相比,得到模型各層加速度反應的放大系數。圖7為模型結構在34條樣本地震動作用下加速度放大系數沿樓層分的布圖,加速度放大系數均值隨著樓層的增高而增大,模型以第一振型為主,呈彎曲變形,變異系數和標準差隨著樓層的增高而增大,表明其離散性亦隨樓層增高而增大。通過MATLAB中的Ksdensity函數可以估計出響應量的概率密度函數。圖8為34條隨機波作用下每層的加速度放大系數概率密度曲線,可以看出其離散性,表現出明顯的隨機漲落現象。隨著樓層的增高概率密度函數趨于扁平,與圖7中變異系數和標準差的變化趨勢吻合。
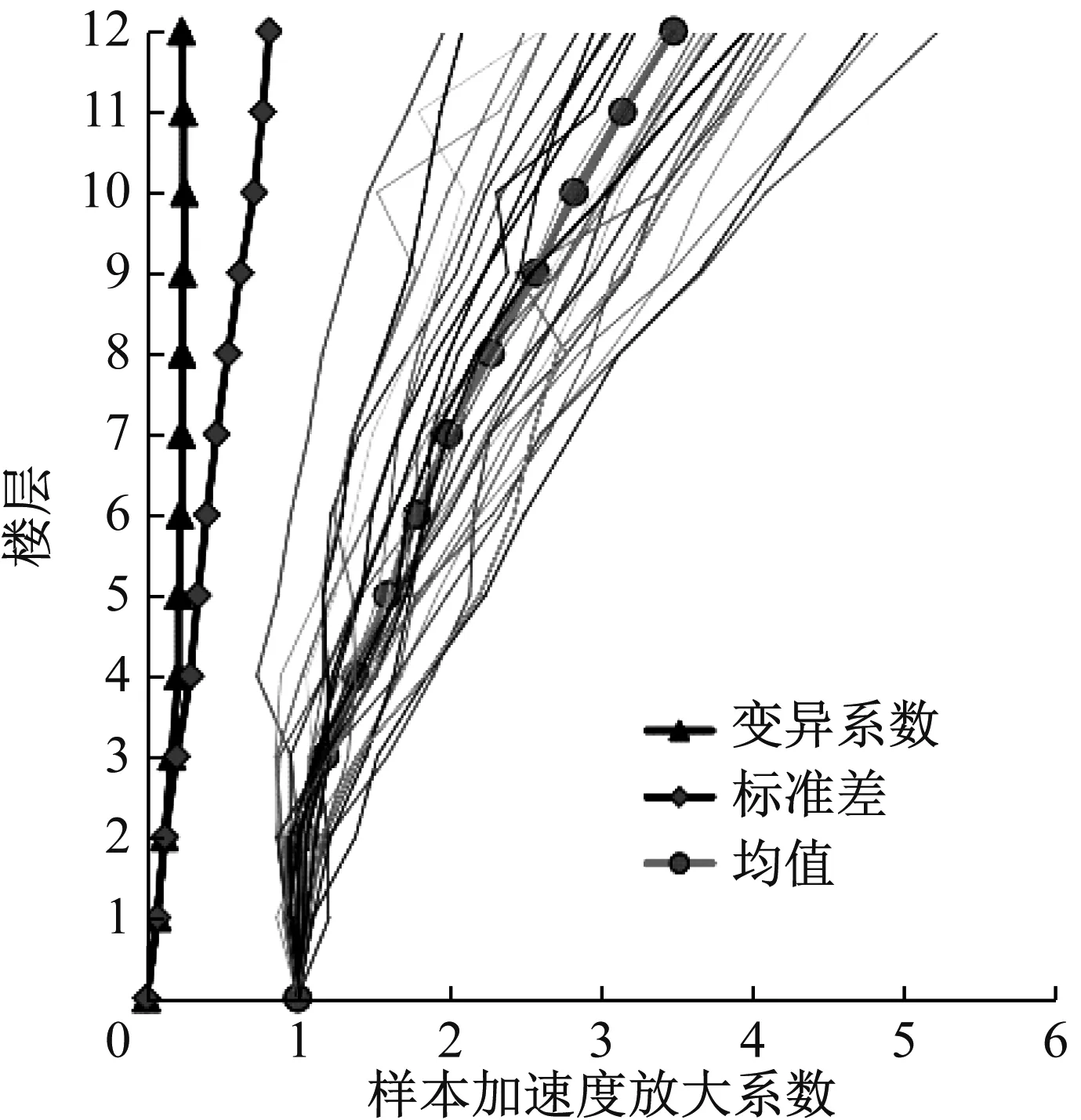
圖7 加速度放大系數均值和標準差Fig.7 Mean and standard deviation of acceleration magnification factors

圖8 加速度放大系數概率密度曲線Fig.8 Probability density functions of acceleration magnification factors
圖9給出了34條樣本地震動作用下層間剪力沿樓層的分布圖。與加速度放大系數相反,樓層剪力是由各個樓層的慣性力累積疊加并傳遞到底部形成基底剪力,導致離散性隨著樓層的降低而增大,基底剪力均值為6.14 kN。圖10給出了樓層剪力的概率密度函數,從圖中可以看出隨著樓層的降低樓層剪力概率密度函數亦呈現出扁平分布趨勢,與圖9的樣本曲線分布吻合。
3.3 模型位移反應
層間側移角是抗震規范中控制結構延性的一個重要設計指標,圖11給出了實測的34條隨機地震動作用下模型結構各層的最大層間側移角。可以發現,層間側移角的較大值發生在第2層和第5層及第11層處,其標準差也在相應樓層處出現峰值,說明這些樓層為該結構的薄弱層。層間側移角均值的最大值出現在第5層,為1/1 767,與試驗過程中第5層連梁處較早出現裂縫相吻合(如圖12所示)。圖13為各個樓層層間位移角的概率密度函數,其均值大多集中在1/4 000到1/2 500,而薄弱層第2、5、11層的概率密度曲線均值偏大,且呈現扁平狀,表現出較大的離散。
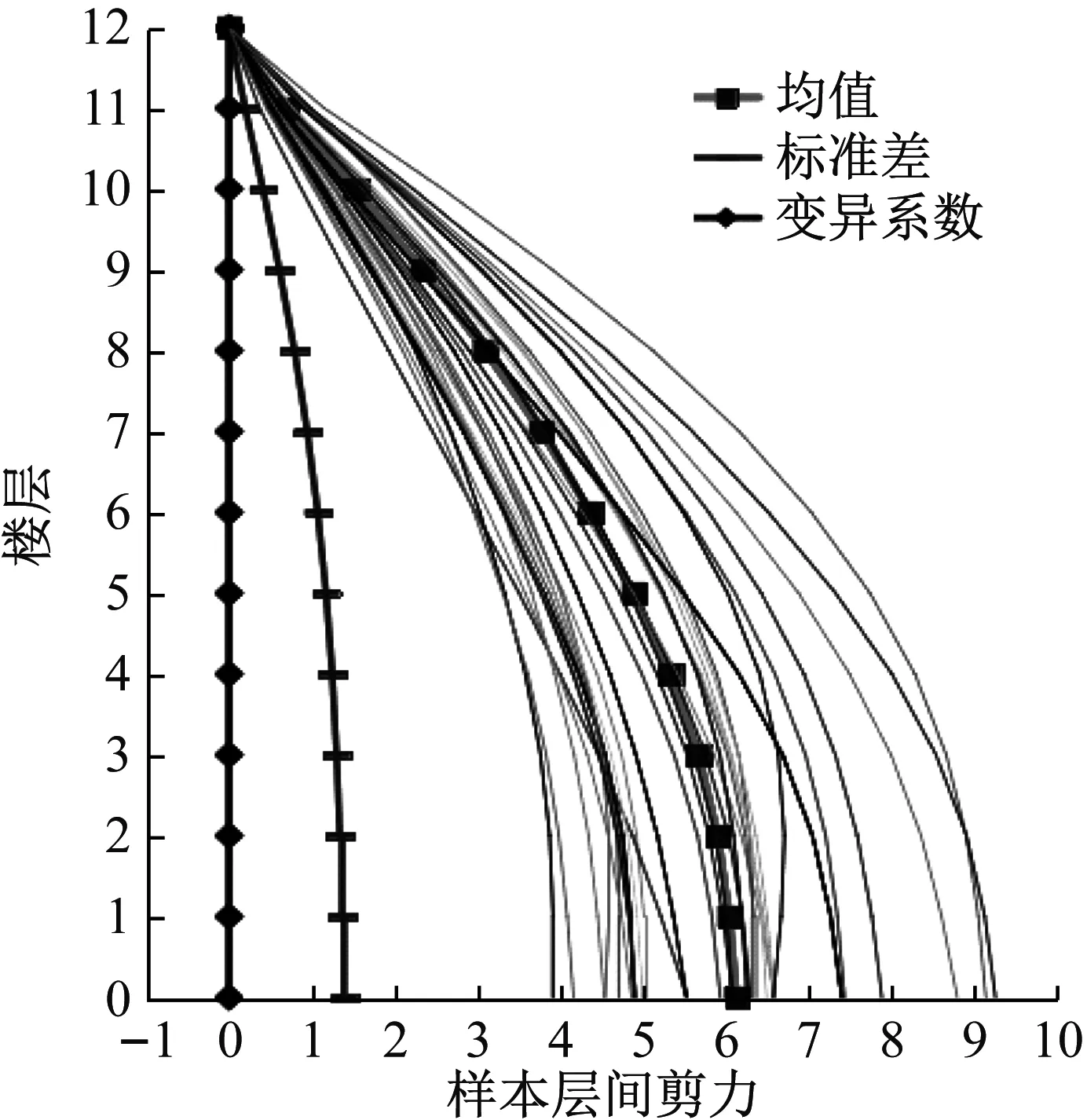
圖9 樓層剪力均值及標準差Fig.9 Mean and standard deviation of floor shear forces
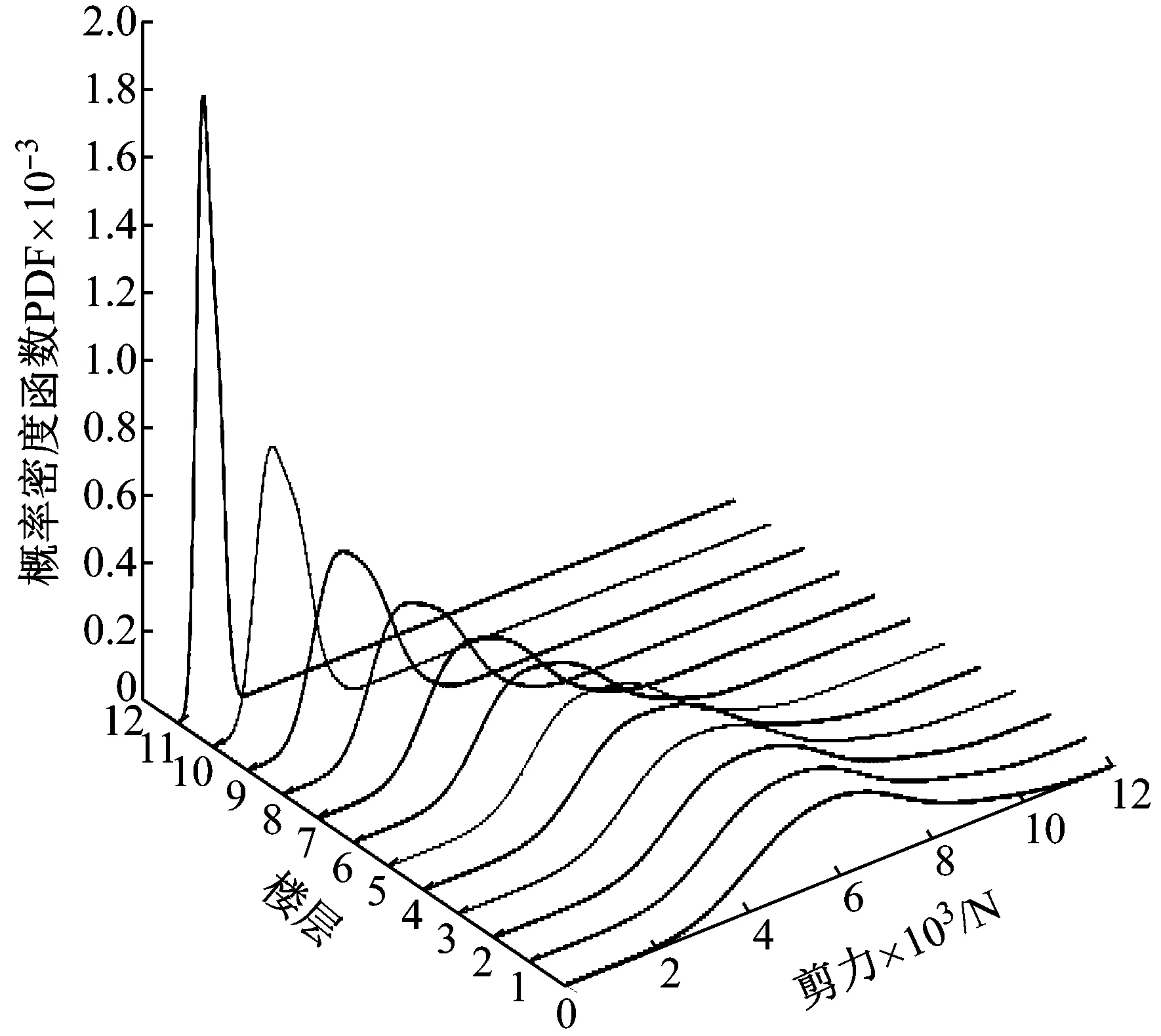
圖10 樓層剪力概率密度曲線Fig.10 Probability density functions of floor shear forces
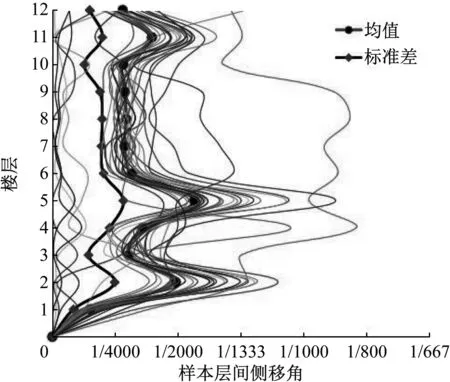
圖11 層間側移角均值和標準差Fig.11 Mean and standard deviation of drift angles

圖12 五層連梁裂縫Fig.12 Crack of a coupling beam at the fifth floor
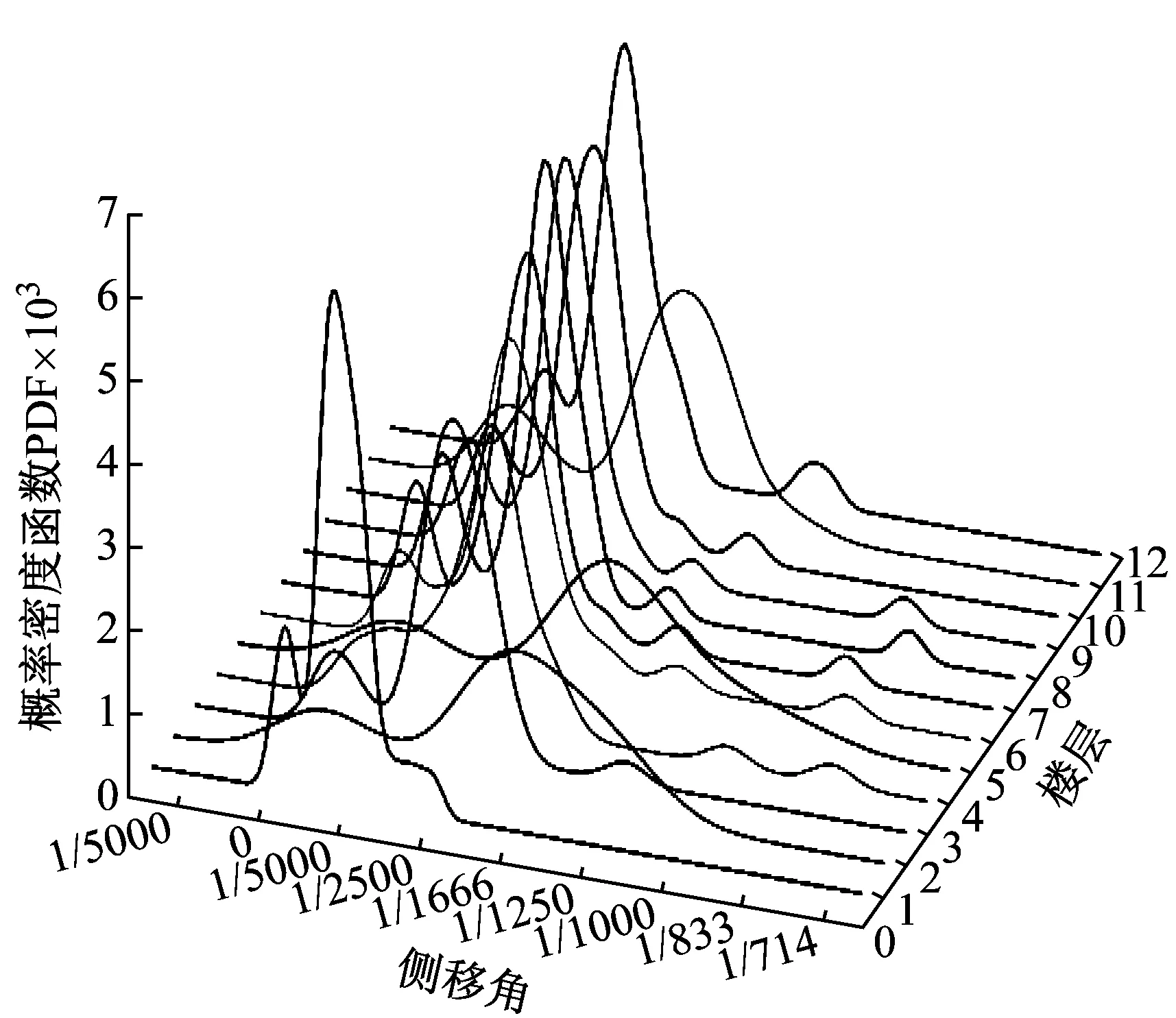
圖13 層間側移角概率密度曲線Fig.13 Probability density functions of drift angles
為了更詳細地分析結構的隨機地震反應,分別計算了模型結構隨機地震反應的均值、標準差及概率密度函數。限于篇幅,本文僅給出最大層間側移角所在第5層側移角的均值、標準差時程及典型時刻的概率密度函數。圖14(a)和(b)為模型結構第5層層間側移角均值和標準差時程,可以發現均值最大的時刻發生在3秒左右,且不超過1/4 000。圖14(c)為典型時刻的第5層層間側移角概率密度函數,可以看出在多遇地震作用下不同時刻地震反應的概率密度函數有所不同,表明結構位移反應具有一定的隨機性。
圖15(a)和(b)是基底剪力的均值和標準差時程,基底剪力的均值發生在2 s時刻約為1 kN,標準差最大時刻也出現在2 s附近。圖15(c)是典型時刻基底剪力的概率密度函數,表現出一定的隨機漲落現象,且與標準的正態分布有差異。
4 結 論
本文設計和制作了1/5縮尺的十二層鋼筋混凝土剪力墻結構模型,基于譜表現-隨機函數方法生成了34條全非平穩地震動加速度樣本,將其作為隨機輸入開展了振動臺試驗研究。通過動力特性測試獲得了模型結構的振型、頻率、阻尼比等。進而,基于結構地震響應樣本分析了加速度放大系數、最大層間側移角、基底剪力等關鍵地震響應的均值和標準差,并估計了典型時刻各個響應量的概率密度函數,討論了離散性沿樓層傳播的變化規律。振動臺響應試驗結果表明,模型結構基底剪力的反應表現出明顯的隨機漲落,且結構反應的概率分布呈非正態分布特征。試驗和分析所得剪力墻結構隨機地震響應可為結構隨機地震反應模擬及可靠度分析提供參考。
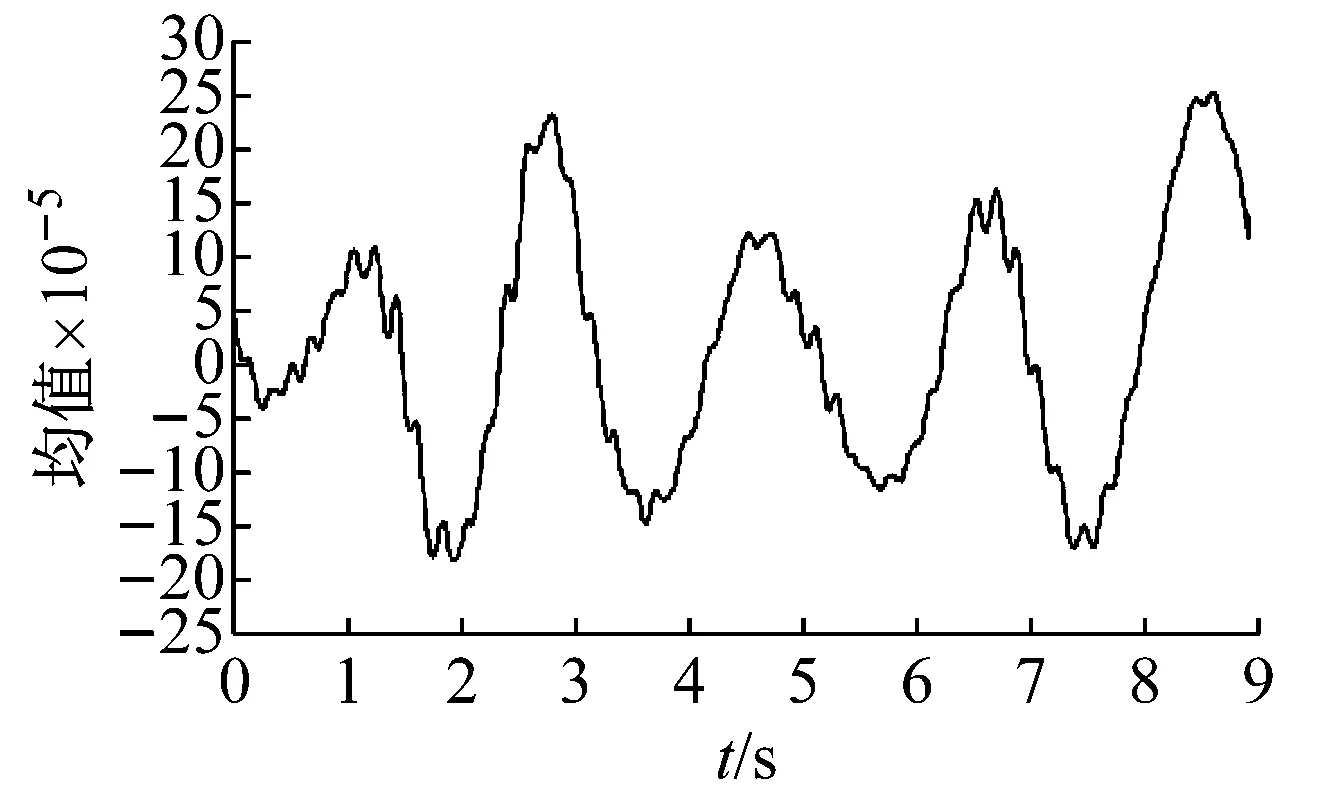
(a) 第5層層間側移角的均值時程
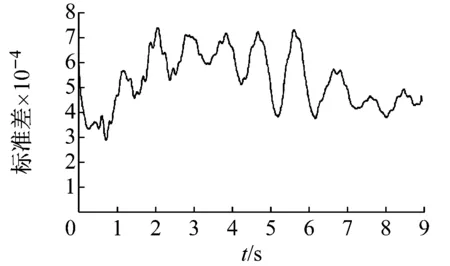
(b) 第5層層間側移角的標準差時程
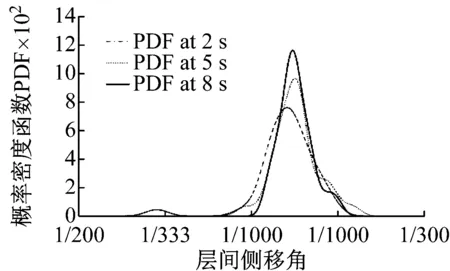
(c) 典型時刻第5層層間側移角概率密度函數
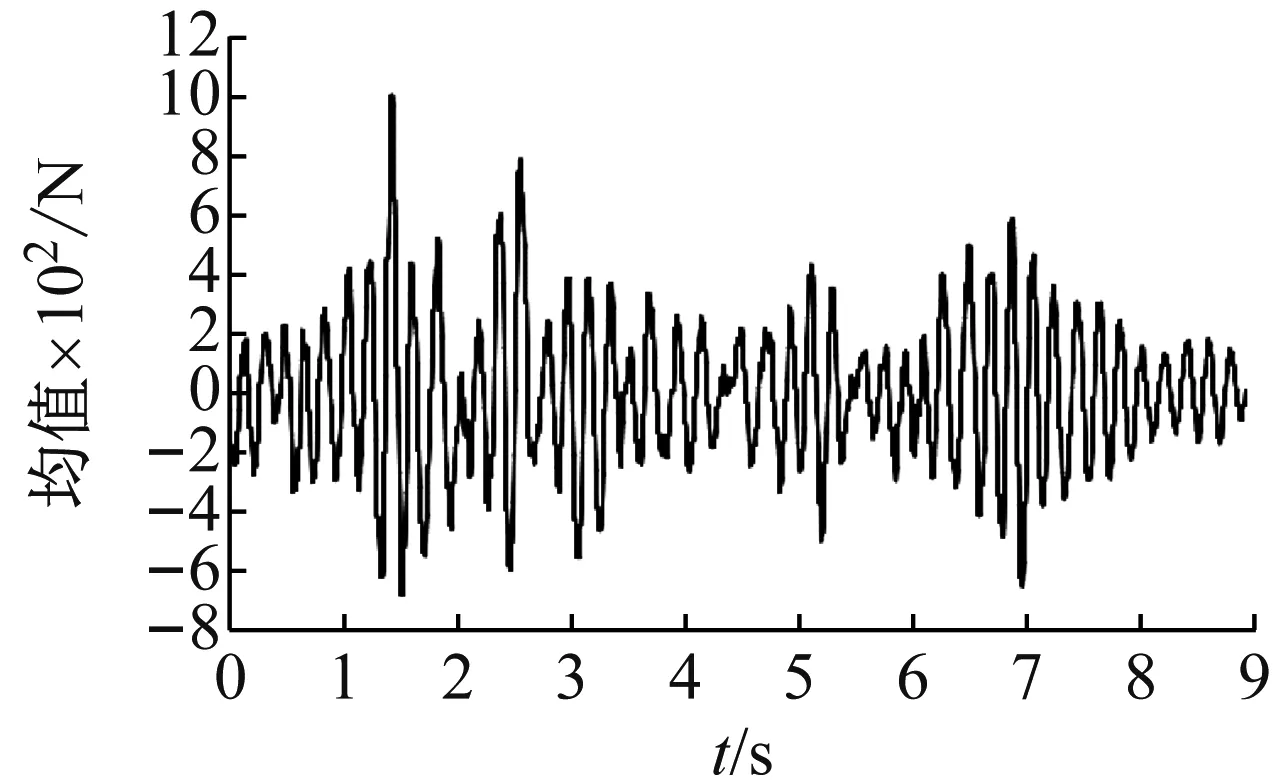
(a) 基底剪力均值時程
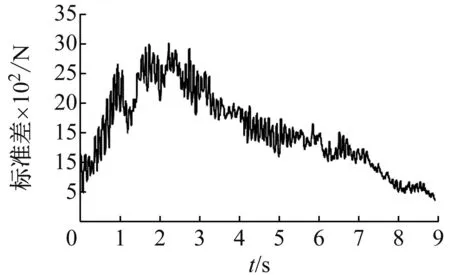
(b) 基底剪力標準差時程

(c) 典型時刻基底剪力概率密度函數

