基于自適應頻帶沖擊強度的滾動軸承故障量化評估
張 龍,成俊良,李興林,楊世錫
(1.浙江大學 機械工程學院,杭州 330027;2.華東交通大學 機電與車輛工程學院,南昌 330013;3.杭州軸承試驗研究中心 博士后工作站,杭州 310022 )
準確可靠地告知設備維護人員何時進行何種維修是設備管理的最終目標,而故障定性和定量診斷是其技術基礎。故障定性診斷即通常所謂的故障診斷,旨在故障發生后識別其性質和發生部位[1],目的是科學指導維修過程,告訴維修人員“如何做”。而近年來漸受關注的預診斷技術(Prognositcs)則側重研究設備剩余有效壽命預知問題[2-5],試圖告訴維修人員“何時做”。
故障量化評估是預診斷和維修決策的基礎,準確評估設備當前故障劣化程度或者說性能退化程度是進行有效剩余壽命預測的前提。故障量化評估常用方法包括簡單參數法和基于特征提取的相似度評估算法等。簡單參數法通常直接從動態信號中提取單一參數來刻畫故障劣化程度,包括峭度(Kurtosis)、歪度(Skewness) 及均方根值(RMS)等。Caesarendra等[6]以峭度作為故障程度量化評估指標,利用邏輯回歸和相關向量機進行故障劣化趨勢預測。Honarvar等[7-8]利用幅值校正后的振動信號的歪度檢測軸承故障,實驗結果表明該指標相比峭度而言對干擾性沖擊不敏感、對載荷和轉速變化的魯棒性更強。RMS因能有效反映動態信號的強度,在實際中應用更為廣泛。Wang等[9-10]在研究軸承預診斷問題時以振動信號通頻帶RMS描述滾動軸承故障程度。李力等[11]將RMS與轉速之比和連續小波能量熵進行加權融合,得到一個軸承故障定量診斷指標。王紅軍等[12]利用速度信號通頻帶RMS(烈度)和特征頻率幅值作為故障劣化程度敏感因子,利用支持向量機對設備劣化趨勢進行預測。
考慮到各種信號處理方法和智能算法在故障模式識別中取得的良好效果,一些基于特征提取和相似度評估的故障程度評價方法相繼被提出。這些方法首先對無故障階段的信號進行特征提取并建立基準模型,最后通過評價測試樣本與基準模型之間的幾何距離或概率依存度來評價測試樣本與無故障狀態之間的相似性,從而定量評估故障程度。如Pan等[13]利用小波包節點能量方法提取軸承振動信號特征,利用支持向量數據描述(Support Vector Data Description,SVDD)建立包圍無故障軸承特征空間的超球體,以測試信號特征向量到該超球體的距離作為軸承健康指標。Shen等[14]基于模糊SVDD空間距離和設備運行時間,研究了具有單調性質的故障程度指標并利用滾動軸承加速疲勞試驗數據驗證了方法的有效性。Yu[15]利用非線性流型方法進行特征降維并建立無故障樣本高斯混合模型 (Gaussian Mixed Models,GMM),將測試樣本屬于該GMM的概率作為軸承健康評估指標。
基于特征提取和相似度評估的方法期望通過合適的信號處理方法進行深層次信息挖掘,以提高故障程度評估的敏感性、一致性和魯棒性等。然而實際應用中尚存在一些問題:① 計算量大,需要進行信號處理、特征提取、基準模型模型建立以及相似度評估;② 計算復雜,SVDD、GMM以及隱馬爾科夫模型(Hidden Markov Models,HMM)[16]等的訓練和測試過程復雜;③ 需要訓練數據,需要無故障階段數據建立基準模型,若設備在獲取訓練數據過程中發生突發故障則無法及時預報;④ 過早飽和,當GMM和HMM等概率型方法表明測試樣本與無故障基準模型之間相似度為零時,設備可能并未完全進入真正的失效狀態,即存在模型極限值早于真實物理失效的情況。上述不足導致基于特征提取和相似度評估的方法在工程實際應用,特別是便攜式巡檢儀器實現上存在困難。
事實上,工程實際中評價機器運行狀態時應用最為廣泛的仍然是時域統計指標如RMS等[17],這些指標具有無需信號域變換、信息損失小、計算過程簡單以及計算量小等優點。其缺點主要是與真實故障程度之間的敏感性和一致性不足等,如RMS與故障發展之間的一致性較好,但對早期故障不夠敏感;Kurtosis能及時發現早期故障,但與故障發展趨勢之間的相關性較差。要解決上述問題,應先了解故障軸承振動特性。當滾動軸承發生裂紋、點蝕、剝落和壓痕等局部故障時,運行過程中損傷點會撞擊與其接觸的其它原件表面,從而產生沖擊力并激勵軸承系統共振。共振解調通過對局部故障沖擊引起的共振頻帶進行帶通濾波去除干擾,并通過包絡解調判斷有無故障和故障發生部位。大部分研究中評估故障嚴重程度時用到的RMS通常是指包括噪聲在內的通頻帶即所有信號成分的有效值,因此并不能純粹地反映故障沖擊強弱。基于此,Li等[18]將3 000~5 000 Hz頻率范圍的RMS作為滾動軸承故障量化指標。然而被激勵的軸承系統共振頻率會隨故障形式、位置和故障程度而改變[19],因此最合理的方式應是針對具體信號自適應選擇最優帶通濾波頻帶。
自適應帶通濾波能夠去除大部分的噪聲干擾信號,但對通帶內的噪聲卻無能為力,因此帶通濾波信號的RMS反映了沖擊信號和噪聲成分總體強度。包絡譜譜峰因子(Crest of Envelope Spectrum,EC)是作者提出的反映信號中沖擊成分強弱的指標[20]。本文將帶通濾波信號的RMS與其EC值的乘積作為滾動軸承沖擊類故障量化評估指標,反映帶通濾波信號中沖擊成分的強度,為故障定量評估提供一種早期故障敏感、一致性好且計算簡單的方法。論文介紹了方法的理論背景,并通過人工植入故障實驗和疲勞試驗數據分析驗證方法的有效性和優越性。
1 自適應頻帶沖擊強度
1.1 復平移Morlet小波濾波器
Morlet復小波定義為高斯函數與復指數函數之積,其時域和頻域表達分別如式(1)和(2)所示
(1)
(2)
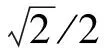
(3)
可知Morlet小波等效于一個通帶為[f0-β/2,f0+β/2]的帶通濾波器。用帶寬參數β代替式(2)中的σ,Morlet小波的頻域表達式可以寫為
(4)
通過選擇不同帶寬β并對中心頻率f0進行平移可得到不同的濾波器,同時因為Morlet小波的時域為復函數,所以這種小波濾波被稱為復平移小波濾波。
連續小波變換本質上是求被分析信號與不同尺度的小波之間的卷積。根據時域卷積定理,小波濾波過程可以采用頻域相乘的方式進行
WT(f0,β)=F-1{X(f)Ψ*(f)}
(5)
式中:F-1表示傅里葉反變換;X(f)為被分析信號x(t)的傅里葉變換。根據Hilbert變換的性質,復小波濾波所得的復信號WT(f0,β)的實部和虛部互為Hilbert變換對,因此可以直接利用式(5)的結果獲取濾波后信號的包絡S(t)
(6)
式中:Re和Im分別表示取實部和虛部。復小波濾波的優勢之一就在于濾波和解調可以同步實現。
1.2 自適應最優頻帶選擇
由沖擊引起的周期性阻尼衰減振動是滾動軸承局部故障的典型特征,也是衡量帶通濾波效果的準則。廣泛應用作帶通濾波器優化目標的Kurtosis只能反映沖擊強弱而不能反映沖擊的周期性,研究表明Kurtosis隨沖擊響應周期性增強反而降低[21]。為此作者提出包絡譜譜峰因子(EC),用于同時度量信號中沖擊成分的能量大小和周期性規律強弱。
設信號x(t)最優濾波后由式(6)得到的包絡信號S(t)的離散形式為S(n),n=1,2,…,N,N為偶數。可由式(7)得到S(n)的頻譜,即最優頻帶包絡譜ENV(m)。
m=0,1,…,N-1
(7)
根據傅里葉變換的性質可知,周期性信號在頻譜中表現為高能量的稀疏離散分量,而高斯噪聲信號的頻譜特性為低幅值的噪聲系列(理論上為常數)。因此,包絡譜中的最大值ENVmax與均方根值ENVrms之比能近似表示包絡譜中周期性成分所占能量比。
ENVmax=max[ENV(m)],
m=0,1,…,N-1
(8)
(9)
包絡譜譜峰因子EC定義為
(10)
為了避免與轉頻相關的故障如齒輪局部故障和轉子碰摩等帶來的影響,上式中ENVmax與ENVrms分別定義為包絡譜ENV(m)在[n×fr,fs/2]范圍內的最大值和有效值,其中fr和fs分別表示軸承旋轉頻率及信號采樣頻率。對于滾動軸承中常見的內圈和外圈局部故障,其故障特征頻率的估計公式分別為內圈BPFI≈0.6×Num×fr,外圈BPFO≈0.4×Num×fr,式中Num為滾動體數量、fr為轉頻。可見,當滾動體數量大于等于5時,兩種故障特征頻率均≥2×fr。因此為排除轉頻等低頻成分在包絡譜中的影響,在計算包絡譜最大值和包絡譜均值時可以舍去2×fr之前的頻率成分,即n可取為2。對于滾動體數量小于5的情況,n則可直接取0,因為通過對濾波器中心頻率f0取值的范圍限制,包絡譜中轉頻影響已很小。指標EC越大意味著濾波后信號的周期沖擊成分所占比例越大,這由沖擊成分的強度和周期性強弱同時決定。
EC用于評價不同的{f0,β}組合的濾波效果及頻帶內沖擊成分的能量比例。設定濾波器中心頻率的尋優范圍為[k×fr,0.45×fs],為排除轉頻故障如轉子和齒輪故障的影響,k可取為40,該范圍可按線性或對數規律均勻分割,取值點數主要考慮計算量與精度的平衡,實驗結果表明100個取值點能得比較滿意的中心頻率尋優結果。帶寬太窄將不足于覆蓋沖擊故障引起的邊頻帶,太寬又會引入更多的噪聲,因此許多文獻推薦帶寬為三倍的最大故障特征頻率[22]。對于外圈固定的滾動軸承而言,其最大故障特征頻率通常為內圈故障頻率(BPFI),所以實際上可以固定濾波器帶寬為β= 3×BPFI。但是為了進一步確保解調結果的可信度,取β=[3,3.5,4,4.5,5,5.5,6]×BPFI,帶寬候選值只有7個,不會過于增加尋優過程計算量。
1.3 自適應頻帶沖擊強度
本文提出自適應頻帶沖擊能量(Shock Value of Selected Frequency Band,SVSB)作為滾動軸承故障量化評估指標,其計算流程如圖1所示。首先根據被測軸承的轉速和結構參數確定軸承故障特征頻率,再結合采樣頻率并由1.2所述以確定Morlet濾波器中心頻率和帶寬參數的尋優范圍。計算尋優范圍內所有{f0,β}組合得到的濾波信號的EC值,其中最大EC值對應的組合即為最優濾波器參數。定義由最優濾波器依據式(5)所得最優濾波信號為Xfiltered(i),則其均方根值Xf-rms如(12)式所示。
Xflltered(i)=Re[WT(f0,β)],i=1,2,…,N
(11)
式中:Re表示取實部。
(12)
本文提出的自適應頻帶沖擊沖擊強度指標SVSB(Shock Value of Selected Frequency Band,SVSB)定義為
SVSB=Xf-rms×EC
(13)
式中:Xf-rms表示自適應選擇的頻帶內信號總強度,EC表明沖擊成分所占的比例,因此SVSB有望能反映信號中單純周期性沖擊成分的強弱并定量反映局部故障的嚴重程度。
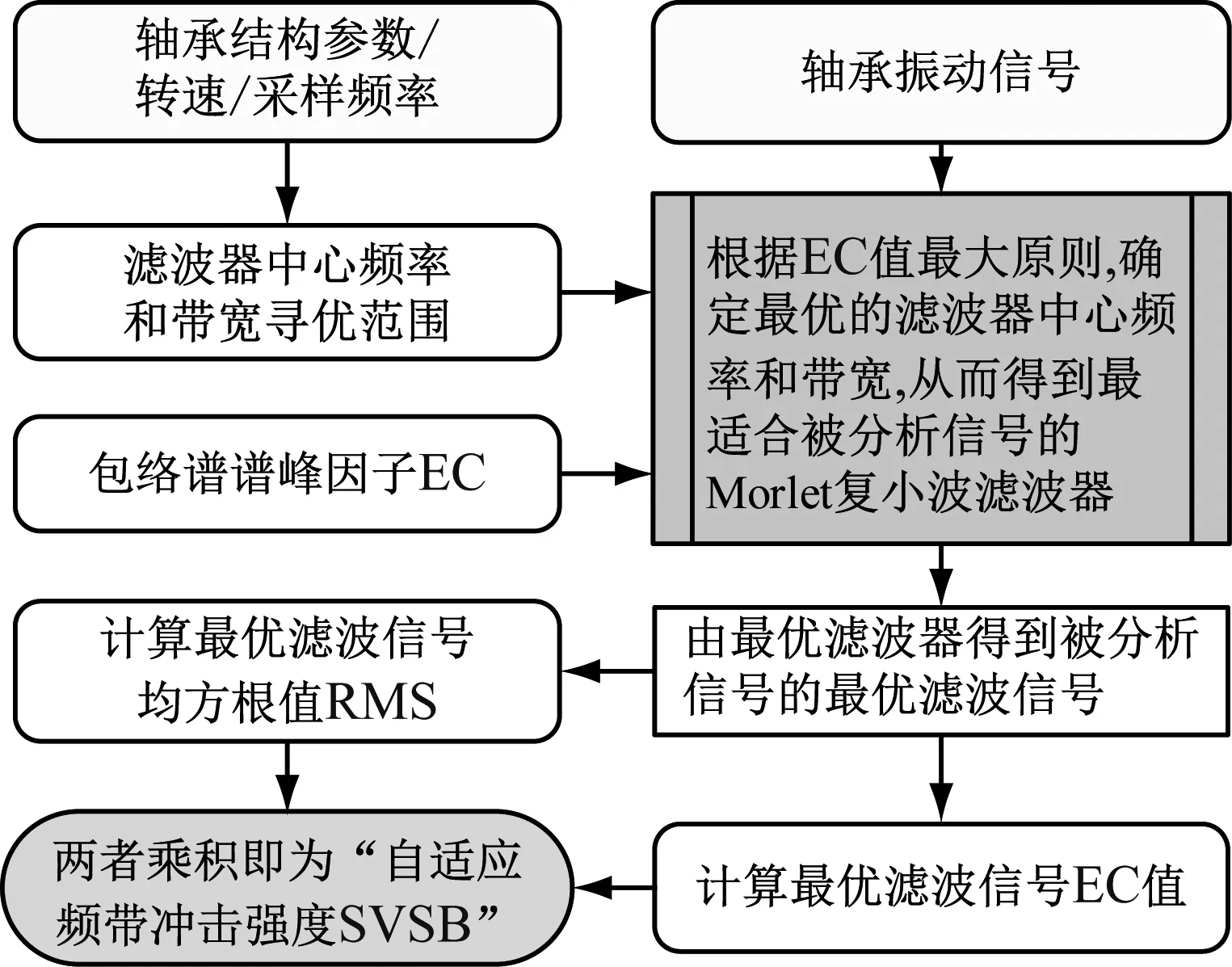
圖1 自適應頻帶沖擊強度計算流程Fig.1 Procedure of SVSB
2 人工植入故障數據分析
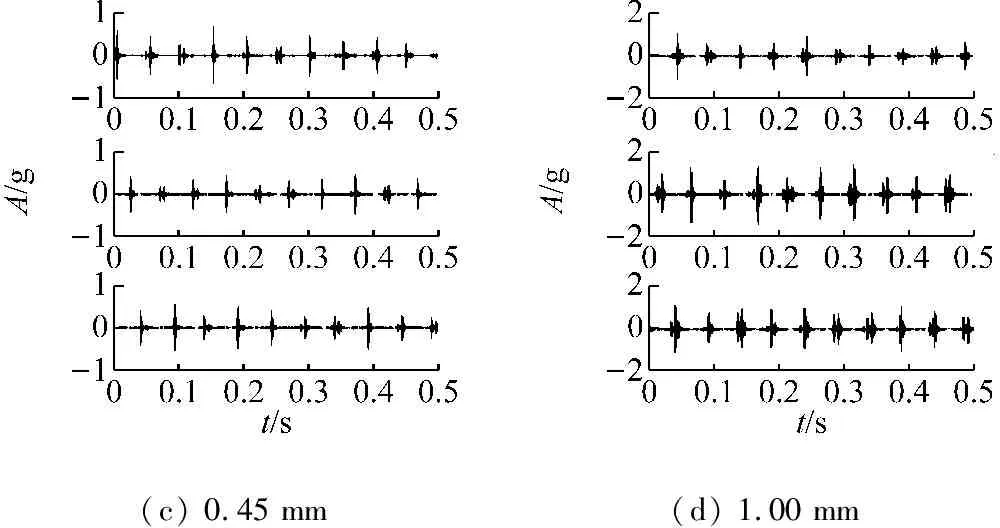
在如圖2所示的軸承齒輪故障綜合試驗臺上進行滾動軸承人工植入故障實驗,試驗臺由變頻電機通過皮帶傳動驅動。試驗臺包括右半部分的齒輪傳動部分和本文用到左半部轉子軸承故障實驗部分。實驗軸承型號為NU205EM內圈可拆式滾子軸承,安裝在最下端的實驗軸承座中。通過電火花加工共模擬了四種不同程度的內圈故障,如圖3所示,凹槽寬度分別為0.05、0.17、0.45和1.00 mm。
加速度傳感器通過磁座安裝在試驗軸承座的上方,采樣頻率為12 000 Hz,軸承內圈轉速為1 218r/min,通過螺旋加載結構向轉子施加80 kgf的力,可計算滾動軸承內圈故障特征頻率BPFI=155.6 Hz。四種不同內圈故障程度各采集3組信號,如圖4所示,可以看到隨著故障程度的加深,沖擊現象越發明顯并且幅值有所增大。圖5給出了12個信號的RMS值及每種故障程度的RMS均值,可以發現除了1 mm故障程度外,其余三種故障程度之間的區別不大,并且0.45 mm故障程度的RMS總體小于0.17 mm情況,這主要是因為兩者故障尺寸相差不大,而0.45 mm時因為沖擊明顯噪聲量減小導致信號總體能量減小。上述現象不利于區別不同故障程度大小并跟蹤故障程度的發展。

圖2 軸承齒輪綜合故障模擬試驗臺Fig.2 Test rig for bearing and gear fault simulation

圖3 不同故障程度的軸承內圈Fig.3 Inner race with different fault
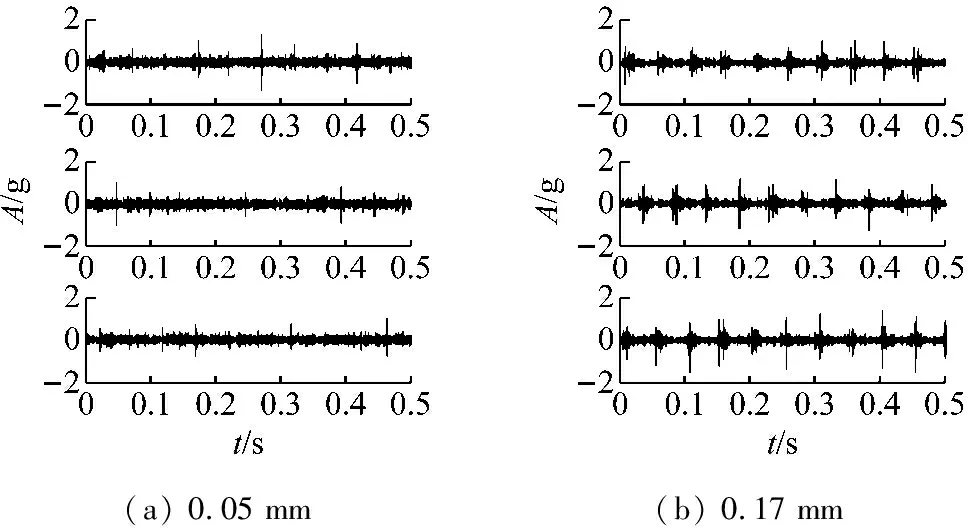
(a) 0.05 mm(b) 0.17 mm
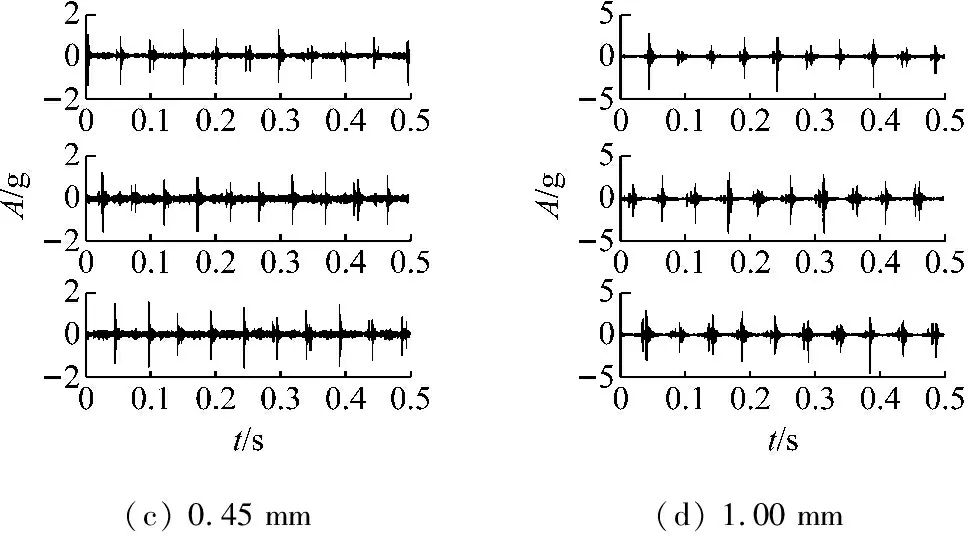
(c) 0.45 mm(d) 1.00 mm
圖4 不同程度內圈故障信號
Fig.4 Vibration of diffferent inner race fault severity levels
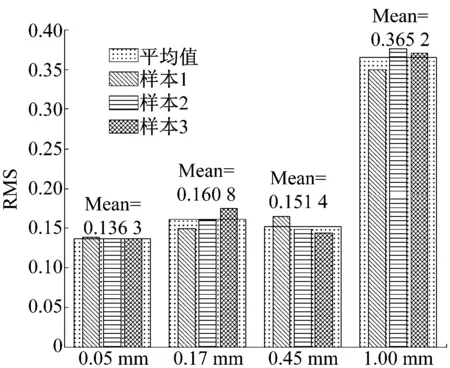
圖5 不同程度內圈故障信號的RMS值Fig.5 RMS values of different inner race fault levels
為此對各信號進行最優Morlet小波濾波,利用EC值最大確定最優濾波頻帶,最終得到的最優濾波器帶寬均為帶寬參數尋優范圍的下限即3×BPFI,因為帶寬過大將使EC值的分母增長速度大于分子,從而EC值下降。所得最優濾波器中心頻率值如圖6所示,可見除0.05 mm故障外,其余各組內信號的中心頻率相差不大,但各組間中心頻率值存在一定差距,說明針對信號本身進行濾波器優化的必要性。圖6中各中心頻率數據點處豎線長度表示最優濾波器帶寬值。0.05 mm故障對應的三組數據中最后一組的中心頻率與前兩組差別較大,可能是因安裝軸承時預緊力大小不一致造成軸承系統固有頻率存在差異。利用得到的最優濾波器對圖4中的各信號進行最優帶通濾波,結果如圖7所示,可見信號中噪聲得到了進一步的消除,沖擊特征得以增強。
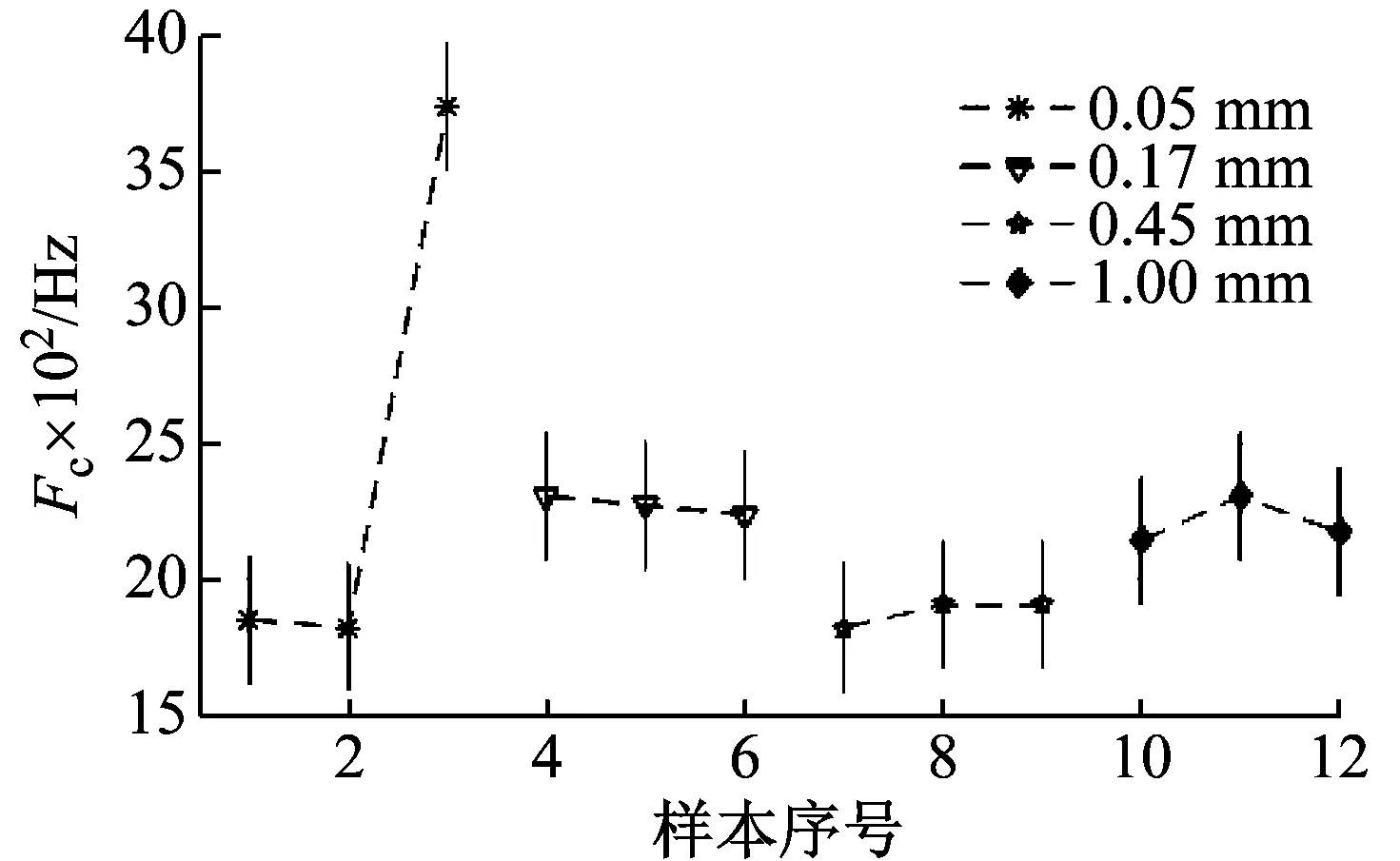
圖6 不同故障程度信號的最優濾波器中心頻率f0Fig.6 The optimal f0 of the signals of inner race faults
計算圖7中各最優濾波信號的RMS與EC值,其乘積即為本文提出的自適應頻帶沖擊強度指標(SVSB)。SVSB結果如圖8所示,可以看到圖5中RMS不能很好區分的0.17 mm和0.45 mm兩種故障情況在此得到了很好的辨識,后者的3個樣本值及平均值均大于前者。且隨著故障程度的增長,SVSB值逐步增長,各不同故障程度的SVSB取值范圍之間不存在重疊,且差別較大,利于不同故障程度的辨識和故障發展趨勢的跟蹤。
圖4原始信號的RMS和圖7中最優濾波信號的RMS、Ec和SVSB值詳細結果如表1所示,從中可以看到各參數隨故障程度的變化情況。
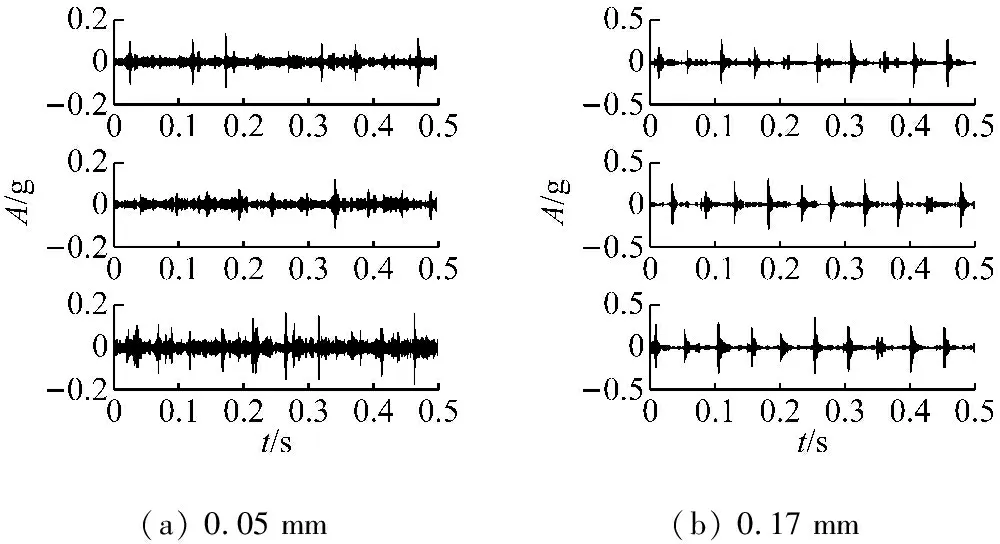
(a) 0.05 mm(b) 0.17 mm
(c) 0.45 mm(d) 1.00 mm
圖7 不同程度內圈故障信號的最優濾波結果
Fig.7 Filtered signals of different inner race fault levels
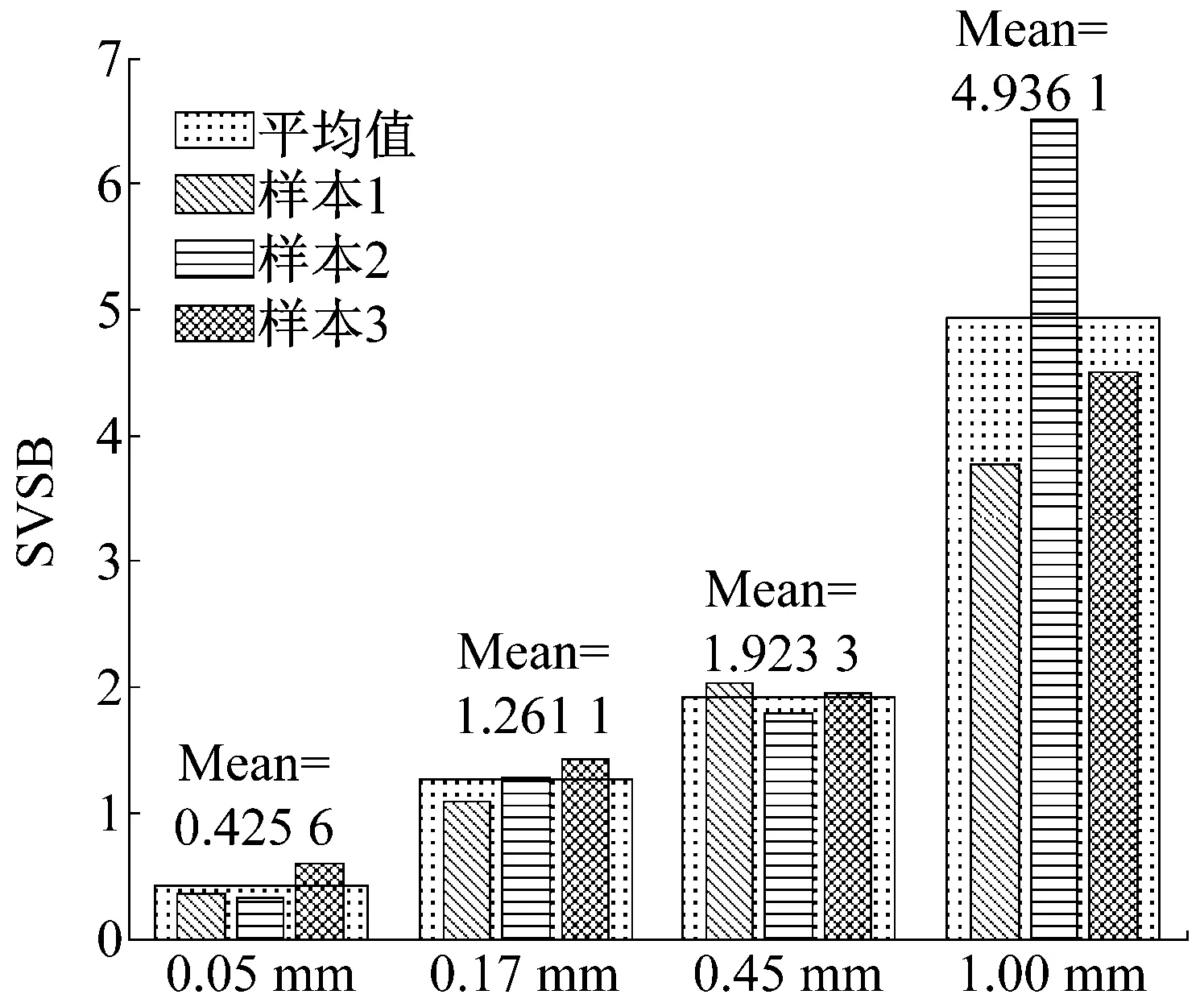
圖8 不同程度內圈故障信號的SVSB值Fig.8 SVSB values of various inner race fault levels
3 疲勞試驗數據分析
上述內圈故障是人為加工制造的,不能完全反映真實使用過程中滾動軸承故障發生發展過程。為了驗證本文方法在自然故障演化過程中的早期診斷及跟蹤能力,對滾動軸承疲勞試驗數據進行分析。實驗數據來源于美國辛辛那提大學智能維護中心,圖9(a)是滾動軸承疲勞試驗臺的整體結構示意圖,圖9(b)是試驗臺局部照片[23-24]。
電動機通過皮帶傳動驅動主軸以2 000 r/min的轉速旋轉。主軸上安裝有四個型號為Rexnord ZA-2115的雙列滾柱軸承,其中兩端的軸承固定在機體上,中間的兩個軸承通過杠桿機構向主軸施加徑向載荷。由轉速及軸承結構參數可知內圈故障特征頻率BPFI = 297.9 Hz。疲勞試驗于2004.02.12 10:32:39開始至 2004.02.19 06:22:39結束,最終解體發現軸承1發生了嚴重外圈故障。試驗過程中通過安裝在軸承座上的加速度傳感器以20 000 Hz的采樣頻率每隔10 min采集振動信號一次,共采集到984個數據文件,每個文件包含4列長為20 480點的數據,本文分析的是第一列。計算984組原始信號的RMS值,結果如圖10,故障發生最為明顯的時刻為703,此時RMS存在階躍。仔細觀察可以發現RMS曲線在No.534和No.703之間,近似按線性規律逐步增大,但是534時刻RMS值為0.084 3,較之前533時刻的0.081 0增長幅值較小,增長比例僅為4.07%,不利于早期故障檢測。
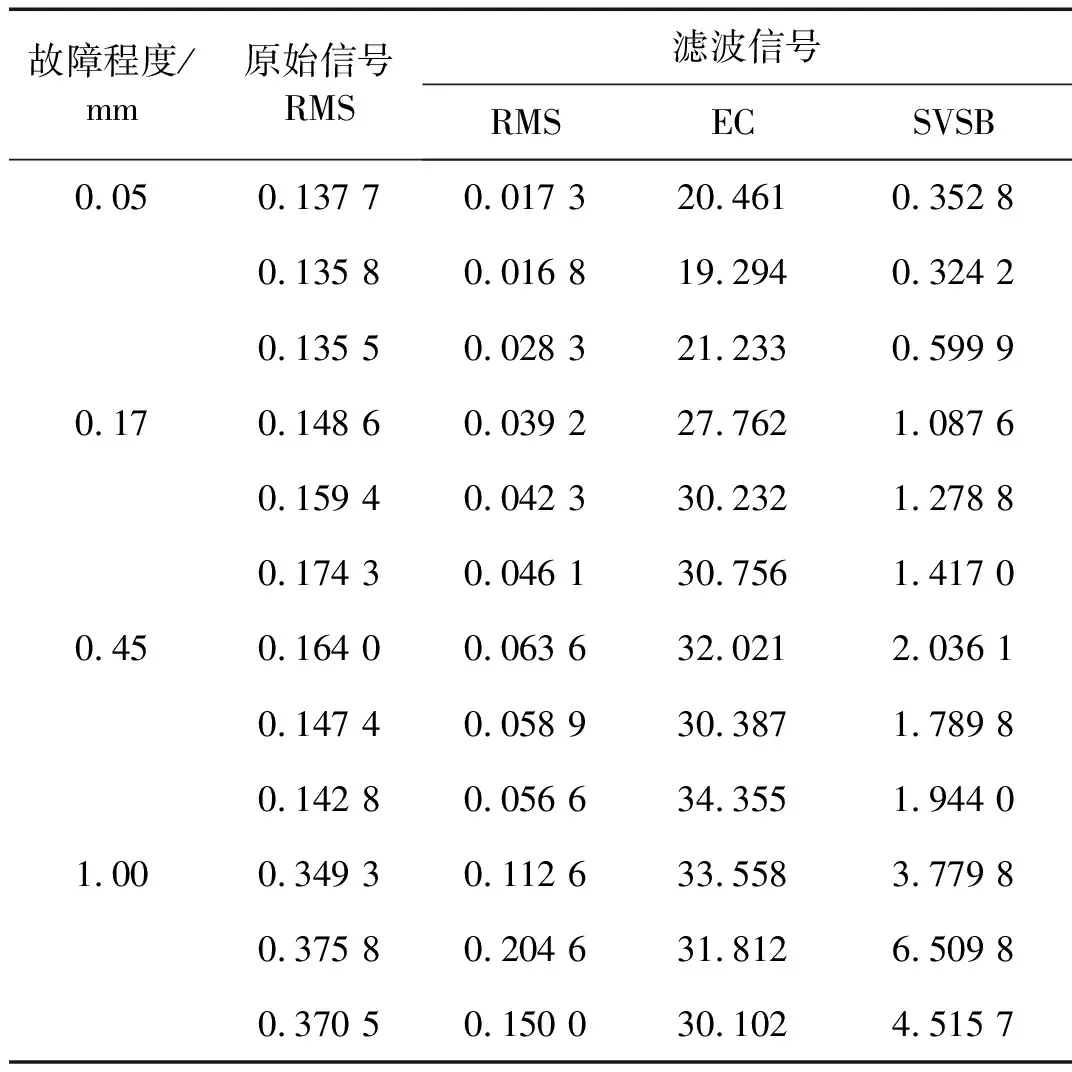
表1 人為植入內圈故障信號各參數計算結果Tab.1 Parameters of original and filtered signals of
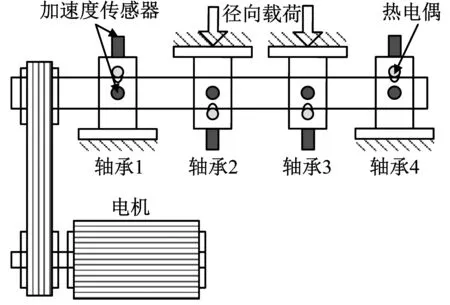
(a) 整體示意圖

(b) 局部照片
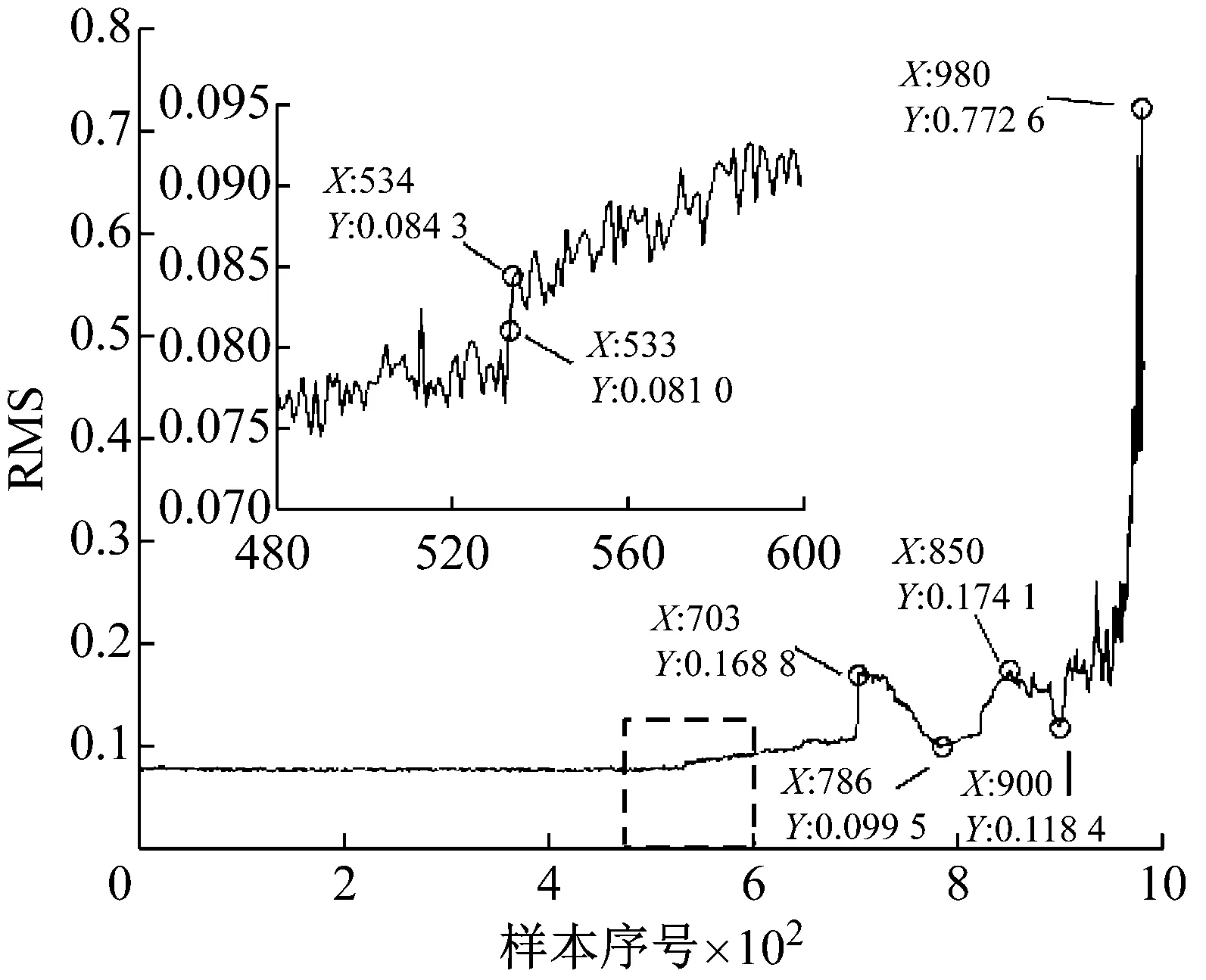
圖10 原始振動信號RMS值Fig.10 RMS of original vibration signals
觀察圖10的RMS曲線可以發現,軸承性能退化過程存在不斷重復出現的“故障出現—劣化—磨平”現象。如534~703時刻即可視作故障出現并劣化的過程,而703~786則是故障剝落點被逐步磨平,沖擊變小。786~850過程中剝落點在原基礎上再次產生并劣化,之后至900時刻再次磨平。整個過程都是剝落點在原來基礎上重復出現和磨平,所以故障總體上在波動中增大,因此RMS雖然存在波動,但總體呈增大趨勢。疲勞試驗過程中典型時刻的時域波形圖如圖11所示,可以看到對應RMS值較小的時刻,如534的早期故障時刻、786和900的剝落被磨平時刻,信號中沖擊成分并不明顯。本文疲勞試驗臺結構單一,所采集的振動信號受外界干擾小,因此RMS反映的信號總體強度水平基本上由信號中的沖擊強度所決定,即RMS在一定程度上反映了信號的沖擊強度。
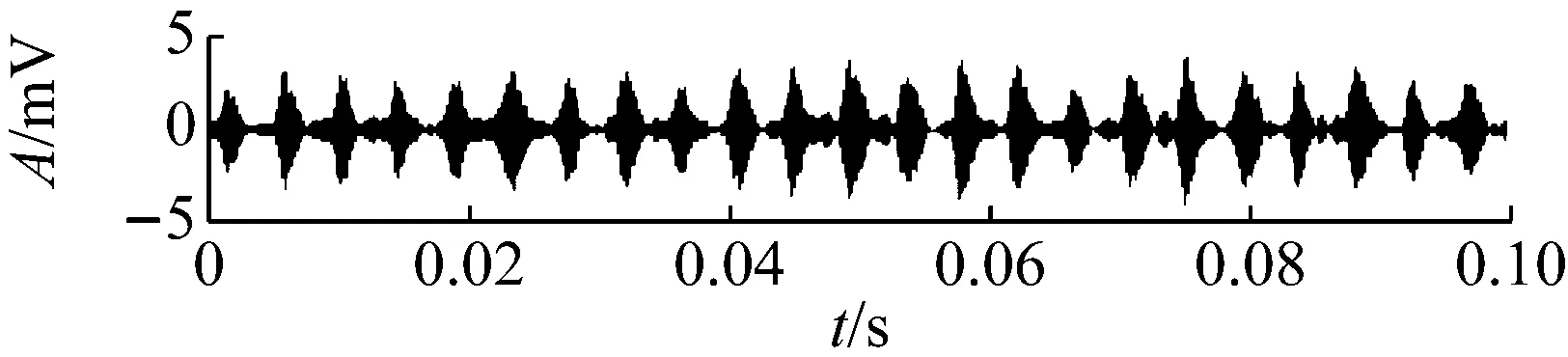
對疲勞試驗過程的984組信號進行最優Morlet小波濾波,所得最優濾波器寬度均為3×BPFI,最優中心頻率則如圖12所示,可以看到中心頻率在早期故障發生時刻534處存在大幅度變化。計算各濾波信號的RMS和EC值,其乘積即為本文提出的自適應頻帶沖擊強度(SVSB),結果如圖13。將SVSB與RMS相比較,可以得出如下結論:① 534時刻的SVSB相對于533時刻的增幅為209.5%,存在明顯陡峭的增幅,因此相比RMS更便于早期故障檢測;② 存在和RMS類似的故障反復出現-磨平現象,說明SVSB同樣能跟蹤軸承性能劣化過程。同時SVSB的故障出現-磨平過程波動幅度較RMS大,說明SVSB能以更為明顯的趨勢描述故障劣化過程。典型時刻的最優濾波結果如圖14所示,相對圖11可以看到噪聲得到抑制且沖擊特征明顯增強。
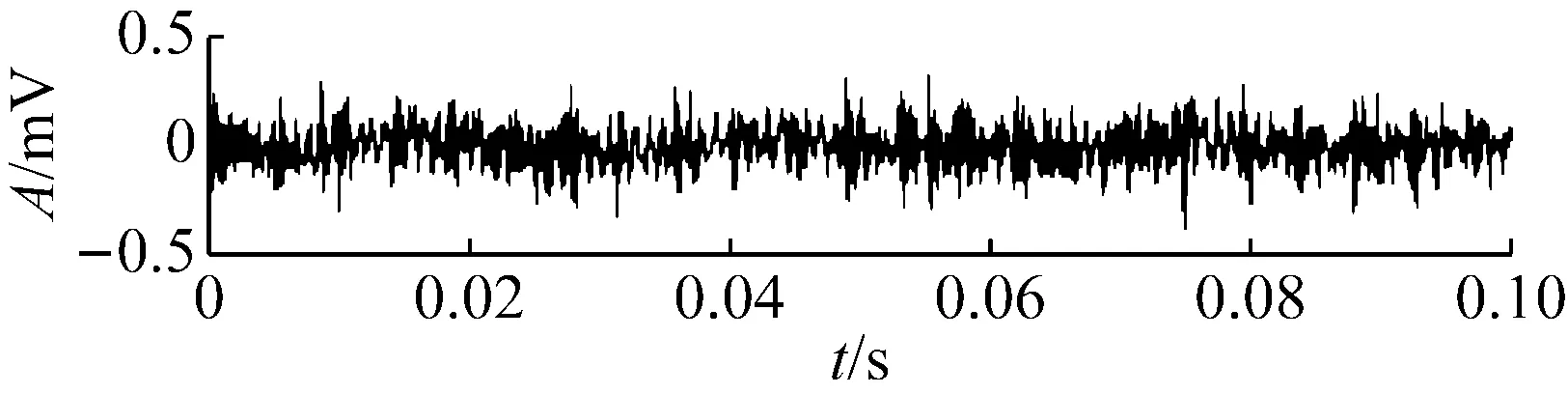
(a) No.534
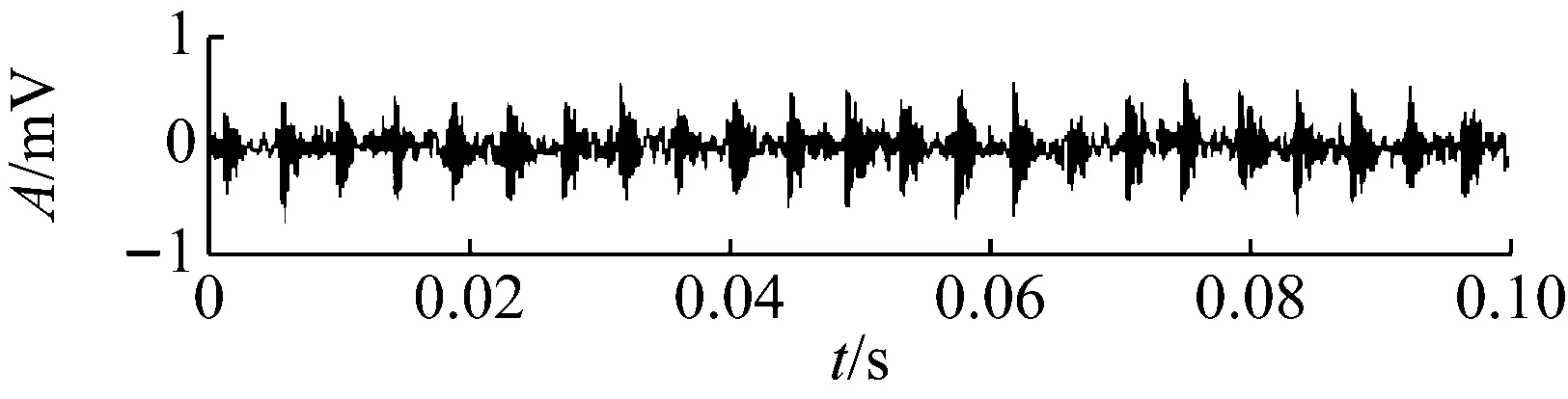
(b) No.703
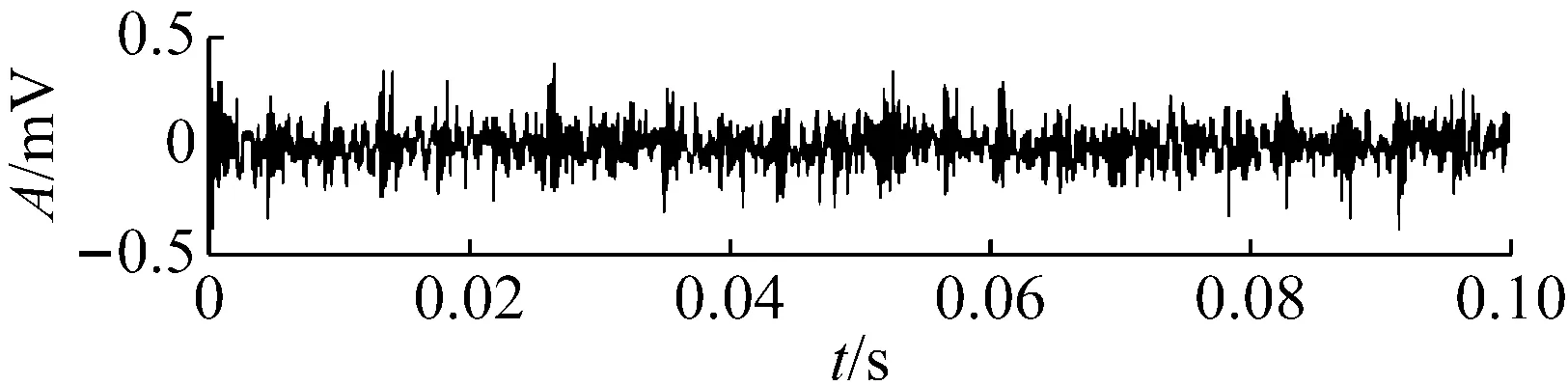
(c) No.786
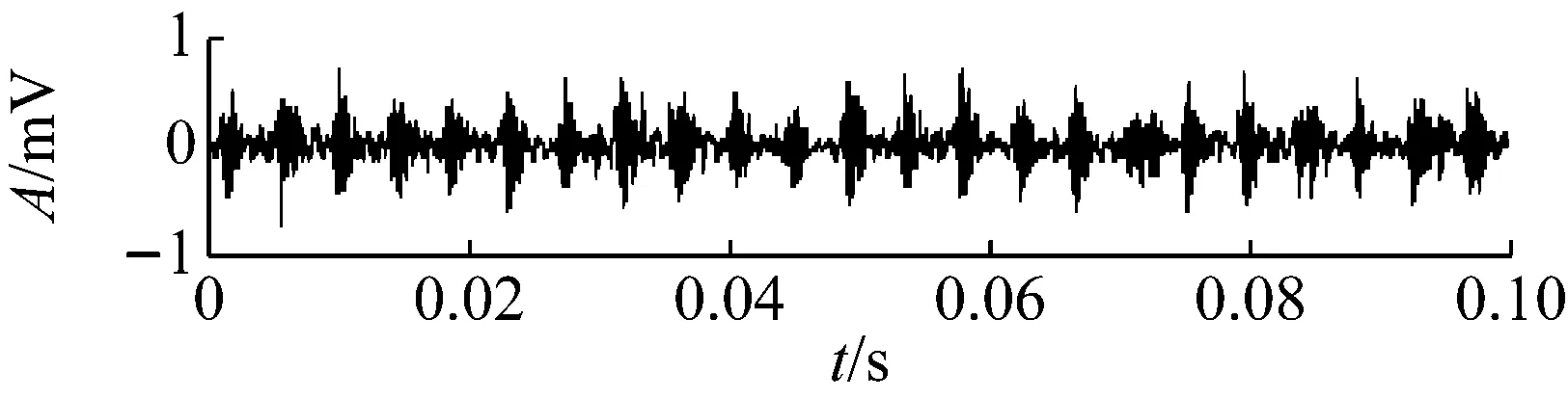
(d) No.850
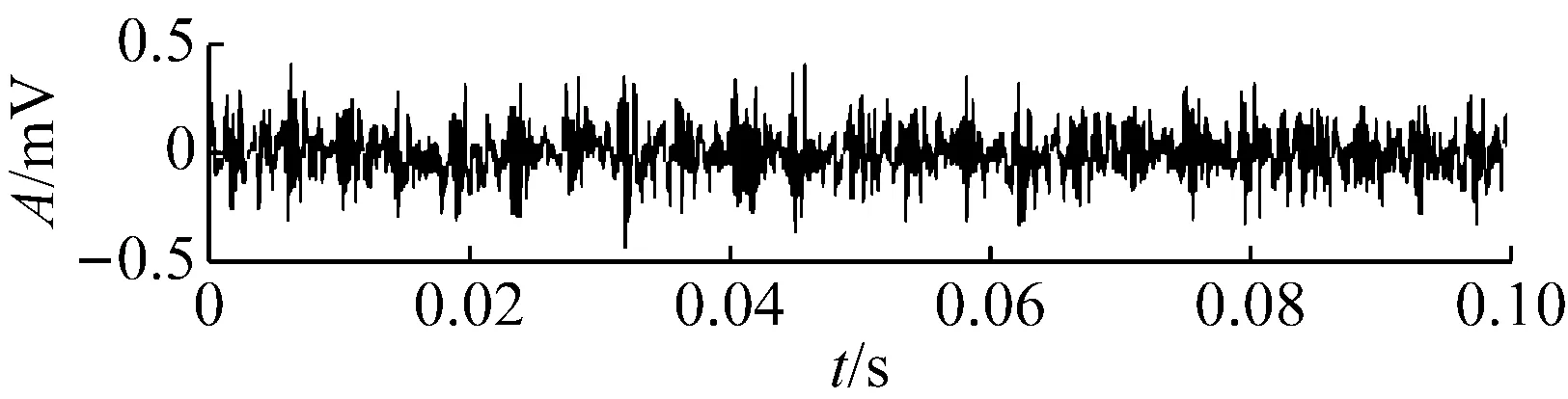
(e) No.900
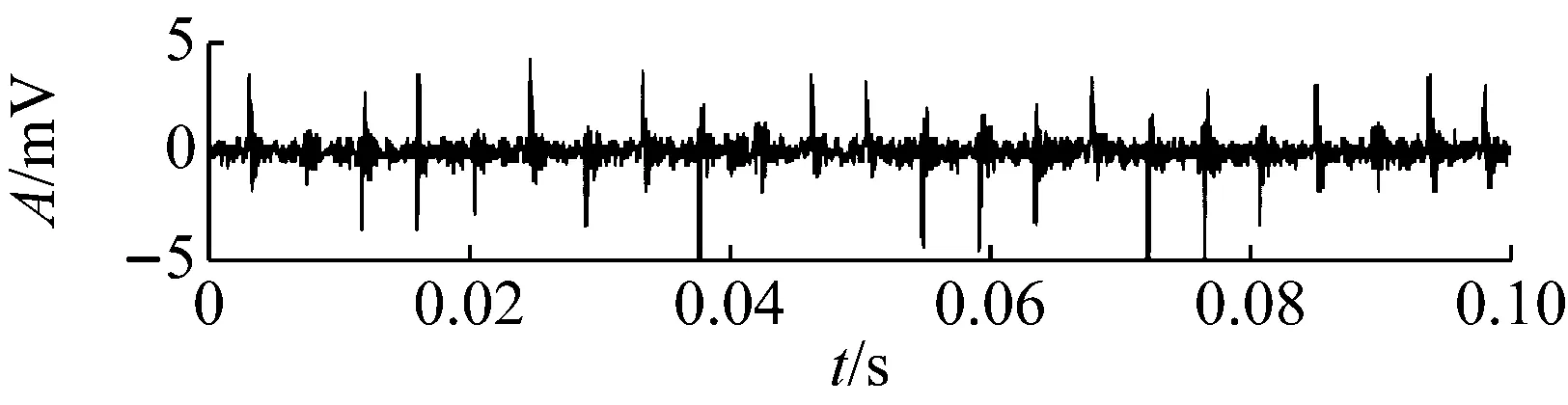
(f) No.980
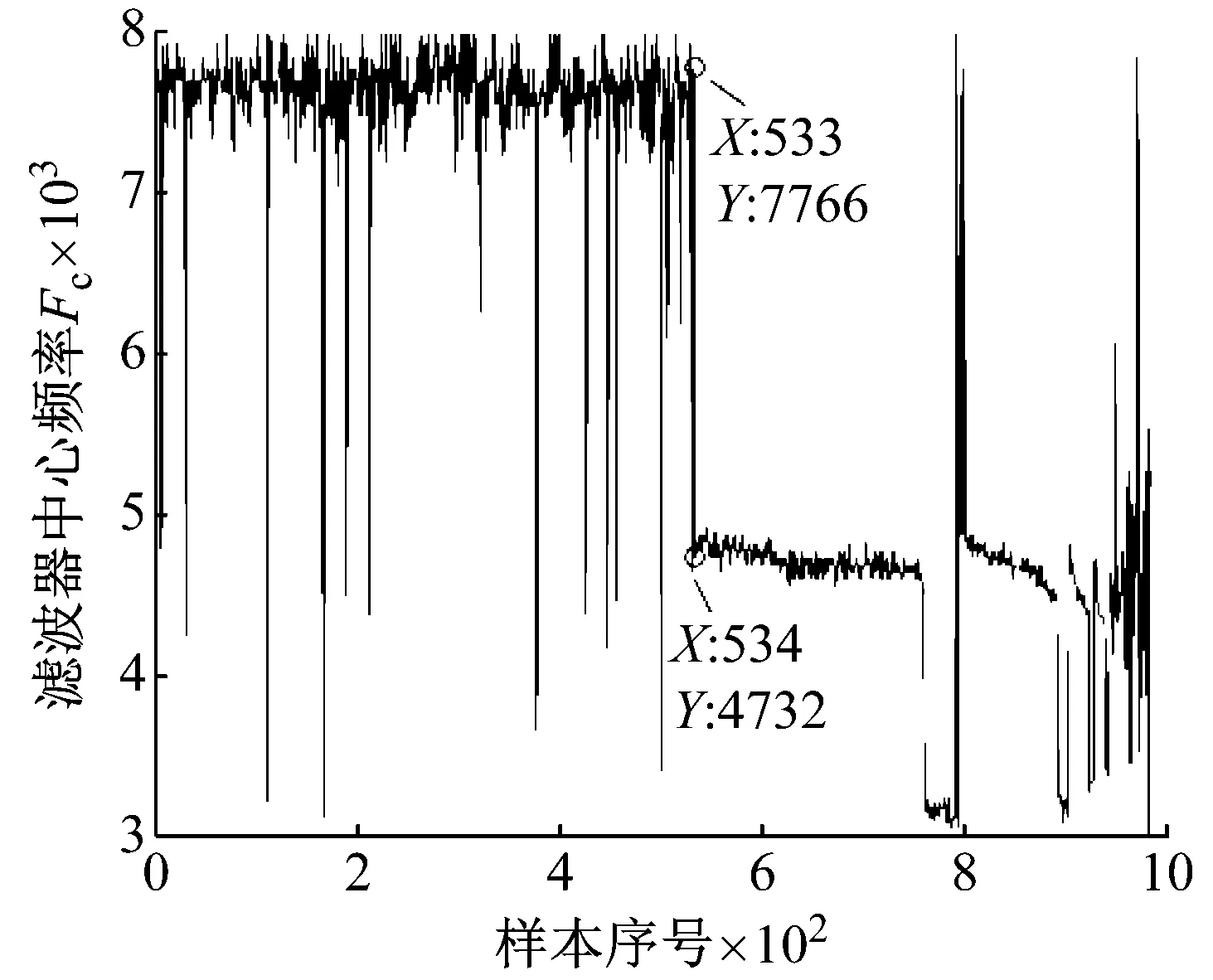
圖12 疲勞試驗濾波器最優中心頻率f0變化過程Fig.12 Optimal center frequency (f0) of run-to-failure test
若將濾波器中心頻率固定在某一個值如自適應濾波中680時刻對應的中心頻率4 636.2 Hz,則所得SVSB結果如圖15所示。可以看到相比于自適應濾波對應的圖13所示的SVSB,圖15的早期故障檢測能力明顯降低,說明了自適應選擇濾波頻帶的必要性。

圖13 疲勞試驗過程SVSB值Fig.13 SVSB of run-to-failure test
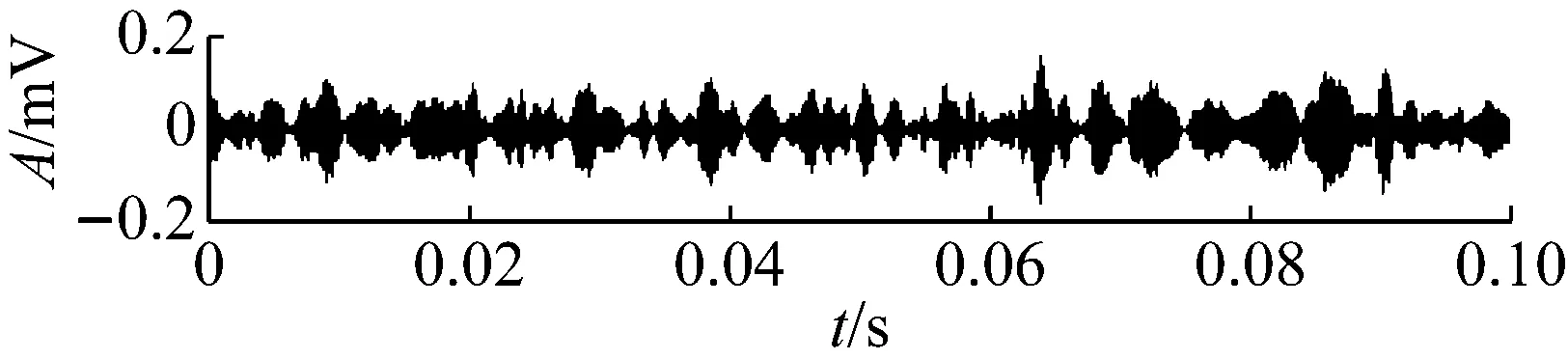
(a) No.534
(b) No.703

(c) No.786
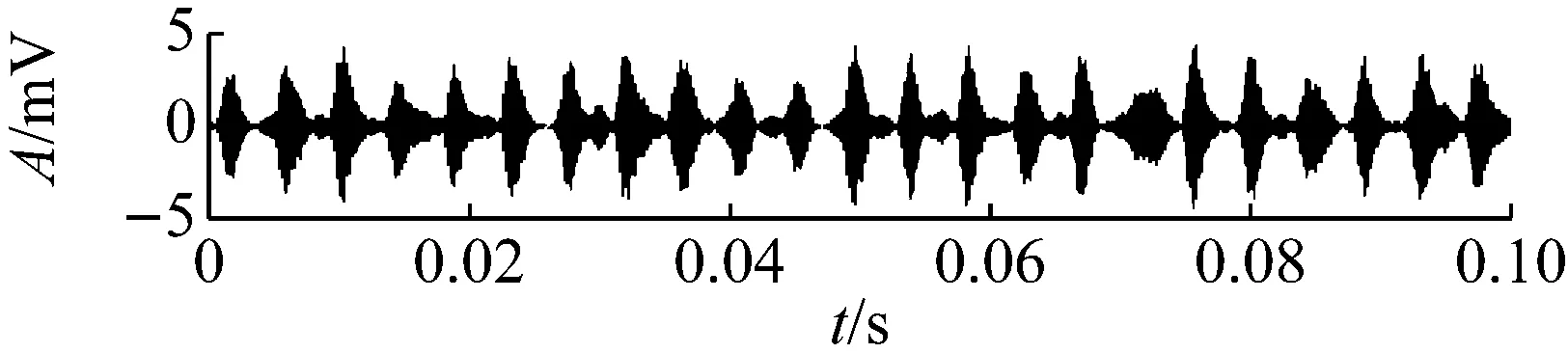
(d) No.850
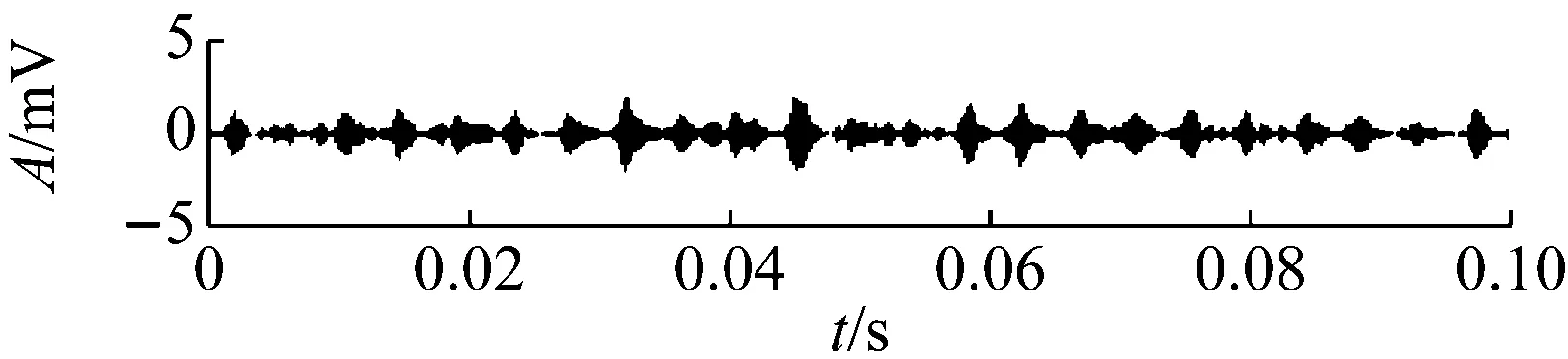
(e) No.900
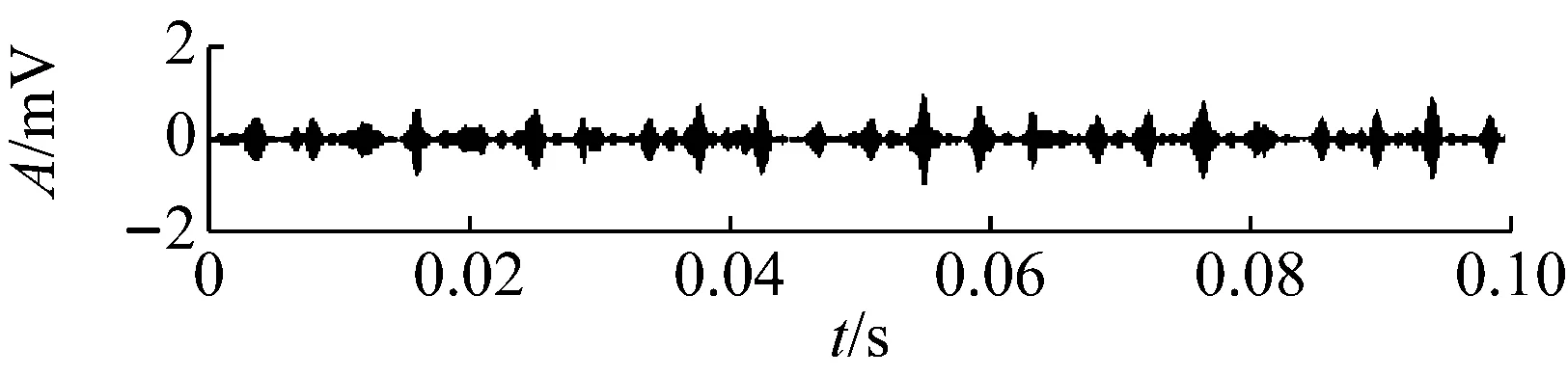
(f) No.980
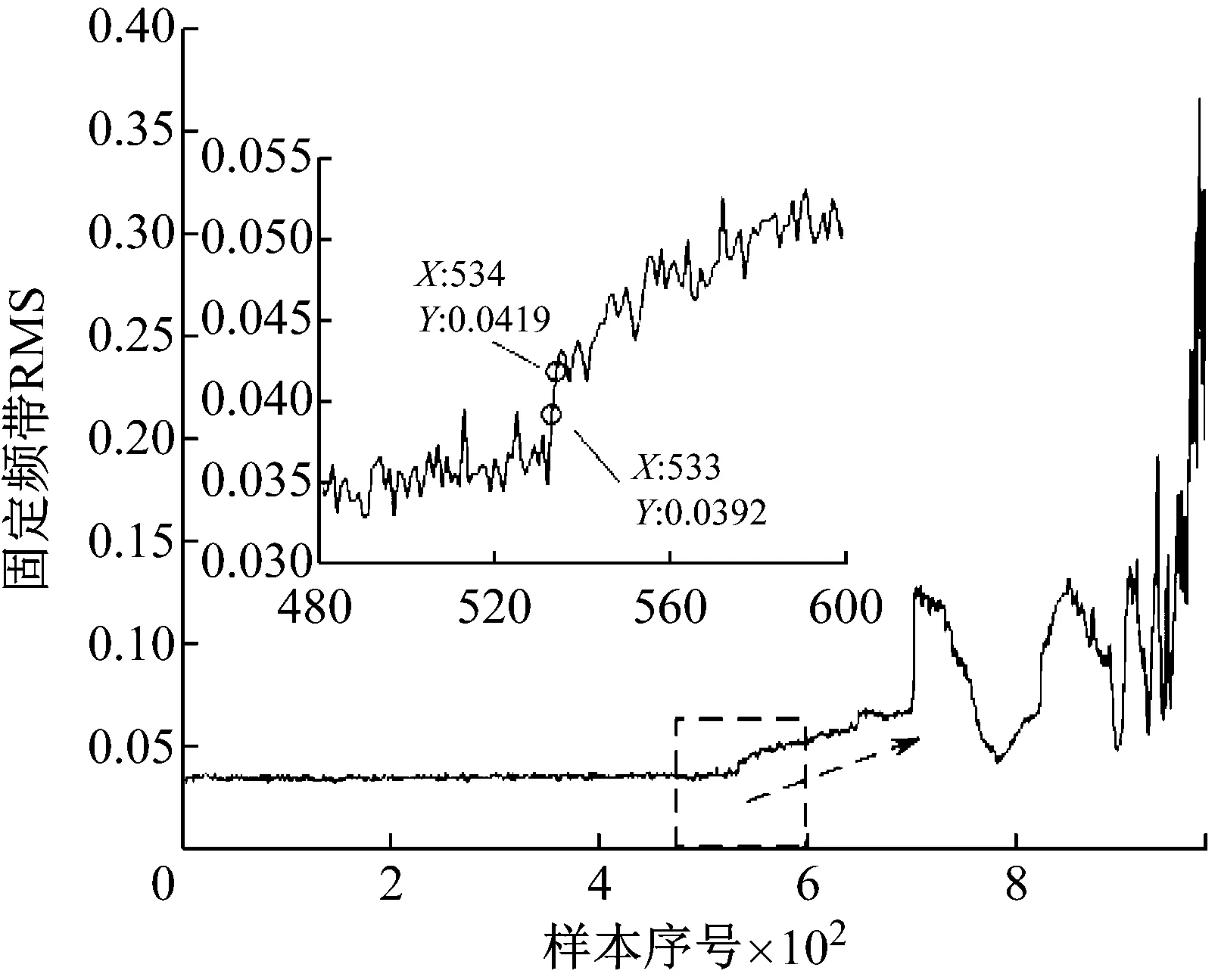
圖15 濾波器中心頻率固定為f0 (680)時的SVSBFig.15 SVSB with keeping f0 equal to f0 (680) = 4 636.2 Hz
4 結 論
故障量化評估是剩余壽命預測和狀態維修的基礎,故障量化指標應具有計算簡單、早期故障檢測能力強及與故障發展趨勢一致性好等優點。針對常規時域方法如均方根值(RMS)不能及時發現早期故障而基于空間距離和概率相似度的評估方法存在算法過于復雜低效等問題,本文提出了一個新的故障量化評估指標——自適應頻帶沖擊強度(SVSB)。SVSB是指利用自適應復平移Morlet小波對信號進行自適應帶通濾波之后,濾波信號的RMS與其包絡譜譜峰因子(EC)的乘積。SVSB中RMS指帶通濾波后信號的總體強度,而Ec表示其中沖擊分量所占比例,因此SVSB能有效反映信號中單純沖擊分量的強度,有望為滾動軸承局部沖擊類故障評估補充一種新方法。
利用人工植入的離散故障程度軸承內圈數據和外圈故障疲勞試驗數據驗證了本文方法的有效性,并與常規RMS進行對比凸顯了本文方法的優越性。

