基于Isight-MSC.Patran/Nastran聯合仿真的弧形閘門動力模型修正

吳思遠，王正中，王 岳，徐 超，劉計良，吳守軍

(1.同濟大學 土木工程防災國家重點實驗室，上海 200092；2.西北農林科技大學 旱區寒區水工程安全研究中心，陜西 楊凌 712100；3.西安理工大學 水利水電學院，西安 710048)

弧形閘門作為水庫大壩的調蓄建筑物，在完成預定復雜工況(靜、動水各開度啟閉)的同時，要保證結構自身穩定，以滿足整體樞紐全生命周期安全運行的要求。通常弧形閘門可簡化為主梁支臂框架體系，其屬于中柔度結構形式[1]，加之啟閉桿及周邊止水對其結構剛度約束有限[2]，在運行過程中，結構失穩破壞問題普遍存在[3]。以往弧形閘門按規范要求，首先應滿足靜力穩定，在此基礎上增加動力安全系數[4]，此類設計方法，存在局部強度雍余，不滿足節能降耗的發展要求，同時忽略了實際工程中所存在的復雜流激振動現象，如強迫振動、自激振動和參數振動等耦合工況[5]。眾多調查結果表明不良振動是閘門破壞的主要因素[6]。因此為了提高弧形閘門設計水平，迫切需要從動力學角度進行結構優化及減振控制研究。而結構動力分析的前提是建立一個合理高效的分析模型。

傳統弧形閘門有限元分析基于原型數據直接建模，而實際結構中，阻尼的不確定性，虛桿、虛板的影響及長期運行造成的銹蝕缺陷等問題，凸顯了有限元建模過程的理想化，而與實際運行工況存在一定差距，導致實踐中危險估計不足，威脅閘門乃至大壩整體運行[7]。而工程人員在進行有限元模型誤差分析時往往僅通過經驗判斷進而改良，缺乏理論依據。同時文獻[8]從弧形閘門建模方式的角度充分說明了除實際結構中所存在的隨機誤差因素外，建模方式的不同同樣會導致結構力學特性的差異。由此可知弧形閘門實測數據與有限元模擬結果難以統一，給進一步結構振動特性分析及振動控制的研究帶來困難，有必要對模型進行優化修正。

現有動力模型修正理論主要包括矩陣型修正法、參數型修正法和基于神經網絡的模型修正方法[9]，在航空及精密制造領域，以往所使用的矩陣型修正法需投入巨大精力，通過精確測量來獲取全模態信息，而在神經網絡的模型修正方法應用過程中，又需反復試算選取網絡模型及隱含神經元，上述兩種方法難以與大型復雜工程實踐相結合。隨著有限元軟件的發展，基于有限元軟件優化模塊的參數型輔助修正方法被廣泛接受。胡仔溪[10]、蘇忠亭等[11]和李志剛等[12]分別基于Nastran和ANSYS有限元軟件，以結構參數(幾何尺寸、彈性模量、密度)為優化變量，對模型進行修正，以此減小結構動力特性實測與仿真間的誤差，梁忠仔等[13]在此基礎上集成多個有限元軟件，發揮各自優勢，提高了優化效率。上述文獻均從有限元模型整體優化的角度分析，以期能提高動力模型精度，但優化變量的選取不合理，其結果改變了真實結構的幾何特性和材料屬性，存在修正過度導致模型失真的問題。同時優化過程局限于某一軟件自帶功能，沒能充分發揮各軟件特色。針對優化變量選取問題，楊世浩等[14]提出利用節點集中質量修正，得到了弧形閘門簡化動力力學模型，但文中并未提及修正方法，不具有廣泛性。王軻基于節點質量重分布，提出了一套詳盡的靜動力模型轉換方法[15]，并給出了相應的模型評估方法[16]，但任存在應用過程中簡單通用、快速優化收斂的問題。

為解決上述問題，本文提出一種基于Isight優化平臺的MSC.Patran/Nastran聯合仿真節點質量特征靈敏度參數優化快速建模方法。Isight是一個將設計過程集成化、自動化的數字化平臺，整合各類仿真軟件及設計流程，并通過內嵌優化算法，實現簡易高效優化設計。

1 特征靈敏度優化分析

特征靈敏度優化是一種參數型優化修正理論，基本思路是以修正模型與實驗模型之間在同一激勵下動力特性的誤差為目標函數，選擇一定的修正量使該誤差滿足最小化，以此來達到優化目的。靈敏度從數學角度表述為：若一函數F(x)可導，對任意變量xJ的一階靈敏度可表示為

(1)

在弧形閘門振動中，變量xJ可理解為動力特性參數(自振頻率和振型相對應的特征值λ和特征向量φ)對結構參數Pl(質量、剛度、阻尼)的改變率，即所謂的特征值靈敏度?λ/Pl和特征向量靈敏度?φ/Pl。對于弧形閘門有限元模型具有N個自由度的黏性阻尼系統，其自由振動運動方程為

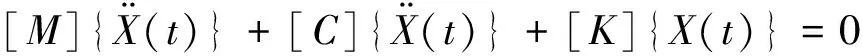
(2)

式(2)中的模態質量特征值靈敏度可展開為

(3)

式中:φik為第k階模態中第i個節點振型值；φjk為第k階模態中第j個節點振型值。

特征向量靈敏度表示為特性向量線性組合的形式

(4)

φs表示第s階模態任意節點處振型值。

在上述特征值靈敏度分析的基礎上，通過泰勒級數展開可得到得到自振頻率與振型修正量為

(5)

(6)

同理，可得到剛度和阻尼特征靈敏度修正量。值得注意的是，特征靈敏度優化方法在不同有限元軟件中所體現的功能具有一定的差別，在ANSYS中，通過概率設計系統(PDS)模塊獲取靈敏度[17]，其實質是Spearman秩相關系數[18]，僅是從概率角度分析不同物理參數(密度、模量、尺寸等)對動力響應特性的影響。而MSC.Nastran提供了設計靈敏度及優化模塊(Design Sensitivity Analysis and Optimization)[19]，以此得到由設計變量改變引起的結構剛度和質量矩陣的偏導，即特征值靈敏度和特征向量靈敏度相對應的設計靈敏度系數，可用于定量分析。

2 弧形閘門優化動力模型設計

本文將結構固有頻率與動力響應作為約束條件，以各節點質量修正量作為優化變量，保證了結構質量、質心、轉動慣量和剛度與實際結構的一致性。在此基礎上運用特征靈敏度優化設計方法，通過Isight-MSC.Patran/Nastran聯合仿真確定設計變量的取值，經過多次迭代使模型與實際結構的動力特性差異趨于最小。

2.1 優化模型

2.1.1 設計變量

以往文獻[10-12]中模型修正基于體型尺寸優化，選取眾多變量，盡管能達到有限元模擬的動力特性與實測結果相符，但模型與實測結構的幾何屬性大相徑庭，結構剛度也隨之改變，造成結構承載力變化，影響結構穩定分析。其次眾多改變量的選取在實質上弱化了修正概念，優化后模型喪失了原有的對稱性及原模型各單元間連接信息。針對上述問題本文僅以弧形閘門節點處質量的修正量Δm作為設計變量X，可表示為

X=(Δm1,Δm2,…,Δmn)

(7)

式中：n為有限元模型節點數。

2.1.2 目標函數

為滿足模型結構各節點相關信息偏差最小的目的，以各節點質量修正量平方和最小為目標函數

(8)

2.1.3 等式約束條件

修正后結構重要幾何特征質量和質心應嚴格滿足靜力學約束條件。

(1) 修正后各節點集中質量之和等于總質量m

(9)

式中：mAi為初步建立的有限元質量矩陣MA中i節點集中質量。

(10)

式中：xi，yi，zi為有限元節點坐標。

2.1.4 不等式約束條件

為保證自變量約束范圍內存在有效解，適當放寬約束條件，加入容許誤差ri。

(1) 各節點集中質量的轉動慣量和與結構的總轉動慣量(Ix，Iy，Iz)約束條件如下

(11)

(2) 自振頻率約束條件為

(12)

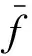
(3) 在有限元軟件分析中，模態振型是一個無量綱相對坐標值，本文中取正則振型，振型約束條件中第k階模態振型可表述為

(13)

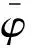
2.2 優化方案

2.2.1 優化算法

上述優化模型屬于非線性規劃，其中目標函數是非線性，而等式約束和不等式約束是線性，可以轉化為二次規劃(QP)問題，標準形式為

(14)

H為n×n階對稱矩陣；Gi(X)為向量函數等式約束與不等式約束在X處的值；Vlb和Vub分別為X的上下限。若優化變量存在全局最優解，式(14)應滿足K-T條件，即要求H為正定矩陣，此時目標函數為凸函數，優化問題為嚴格二次規劃。

根據本文優化目標，轉化成標準形式

(15)

H正定，故本文優化結果存在全局最優解。本文基于Isight采用序列聯系規劃法(DONLP)，此方法是對拉式函數H矩陣的Pantoja-Mayne更新，其對armiji-type算法改進，對變量上下界采用類梯度法處理。

2.2.2 Isight-MSC.Patran/Nastran聯合仿真

首先在Patran中建立弧形閘門有限元幾何模型，賦予材料屬性得到初始模型，獲取模型幾何特征，即總質量、質心和慣矩，并采用集中質量法進行模態分析提取質量矩陣(每個元素作為優化變量對應模型各節點質量)。然后把獲取的質量矩陣離散至不含密度屬性的有限元模型上，得到集中質量分布模型，再通過模態分析獲取集中質量分布模型的自振頻率和正則振型，利用靈敏度分析模塊獲取各節點質量對應的頻率和振型響應的靈敏度。利用Isight提取的相關信息進行優化計算，從而得到質量修正量Δmi，通過修改bdf文件，導入Nastran中進行動力分析，獲取自振頻率并預設收斂準則，迭代誤差依據實測與初始集中質量有限元模型自振頻率相對誤差大小決定。循環上述過程即可得到準確的弧形閘門動力有限元模型，并獲取自振頻率與振型數據，通過模態置信度準則MAC和頻率相對誤差進行誤差判斷，控制流程圖如圖1所示。

3 方法驗證

某高水頭弧形閘門的主框架有限元模型如圖2(a)所示(水電站機電設計手冊編寫組1988)，圖中圓圈的編號為節點號，有限元模型共有16個單元，17個節點，每個節點有3個自由度。構件截面尺寸如圖2(b)所示，主梁采用工字形截面，彎曲平面內的慣性矩Ix1=1.235×10-2m4，單位長度質量m=430 kg/m；支臂采用箱形截面，彎曲平面內的慣性矩Ix2=2.319×10-3m4，單位長度質量m=386 kg/m；彈性模量E=210 GPa[20]。以上述模型為無誤差狀態，在此基礎上，將第3、7、12號節點集中質量+5%～+40%的攝動，4、8、14號節點集中質量-5～-40%的攝動，以模擬建模誤差，同時保證總質量不變，具體參數如表1所示。

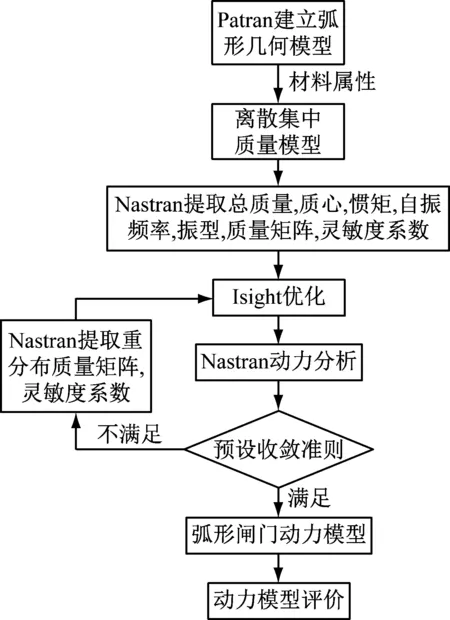
圖1 Isight-MSC.Patran/Nastran聯合仿真流程圖Fig.1 The joint simulation flowchart of Isight and MSC.Patran/Nastran

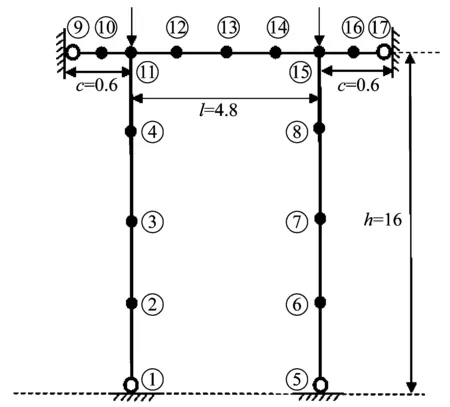
(a) 主框架有限元模型(m)

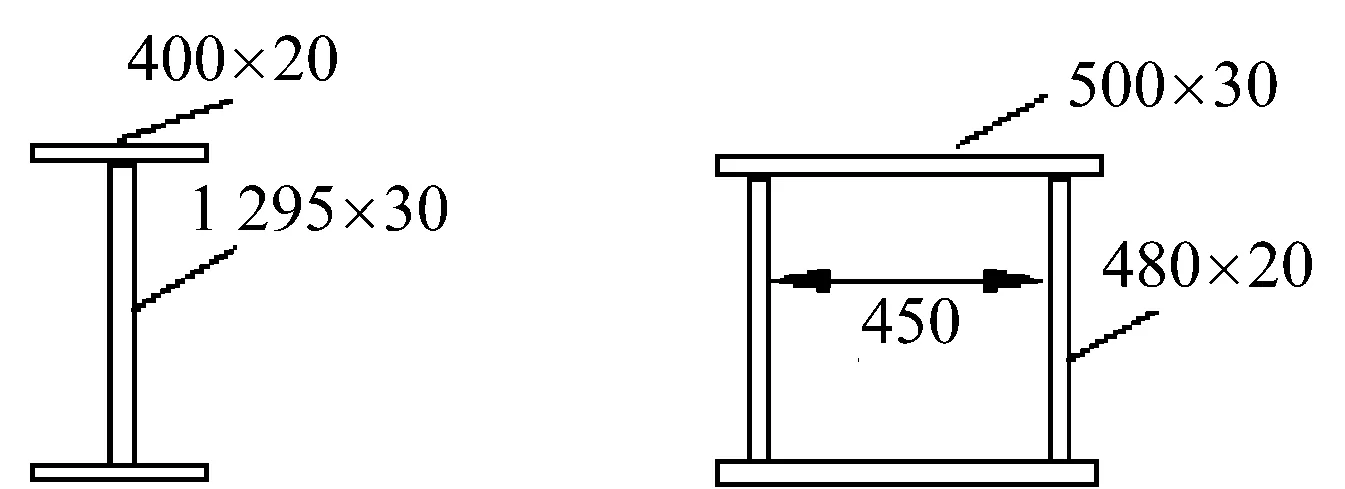
(b) 構件截面尺寸(mm)

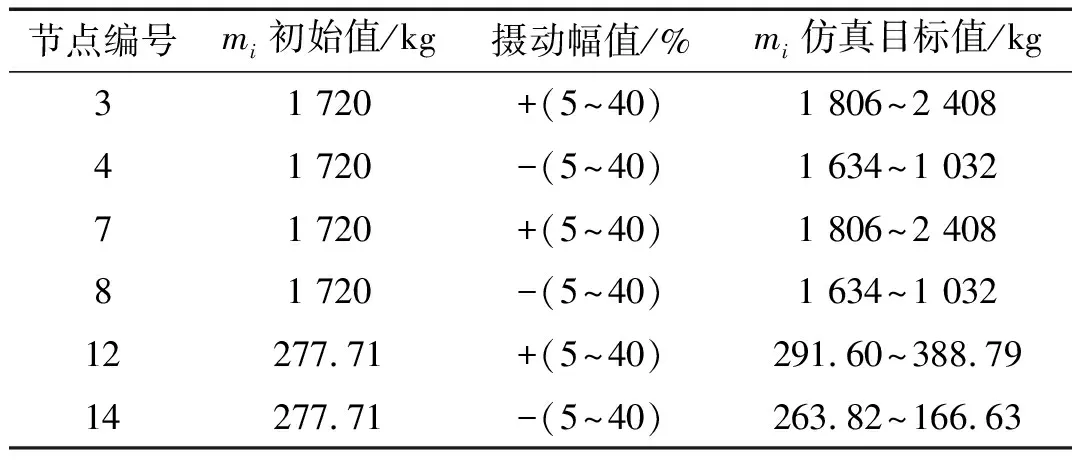
表1 節點攝動誤差Tab.1 Node modeling error

利用本文方法對初始有限元模型進行修正，可得到相應的優化模型與目標頻率相對誤差迭代收斂曲線。

由圖3計算結果可知，本文方法可識別并修正攝動誤差，經五次迭代優化后有限元模型與目標頻率最大誤差小于1%。以此說明本文方法能夠快速建立滿足目標狀態下振動特性的結構動力有限元模型，進一步驗證了本文方法實際應用的可能性。

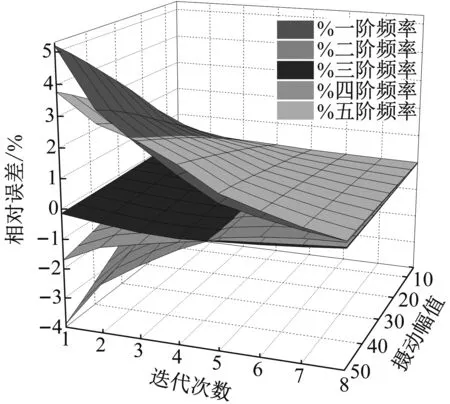
圖3 誤差迭代收斂曲線Fig.3 Identified error convergence curve

在上述驗證基礎上與文獻[10-12]有限元多參數變量優化方法進行對比，優化結果及力學特性分析如表2。

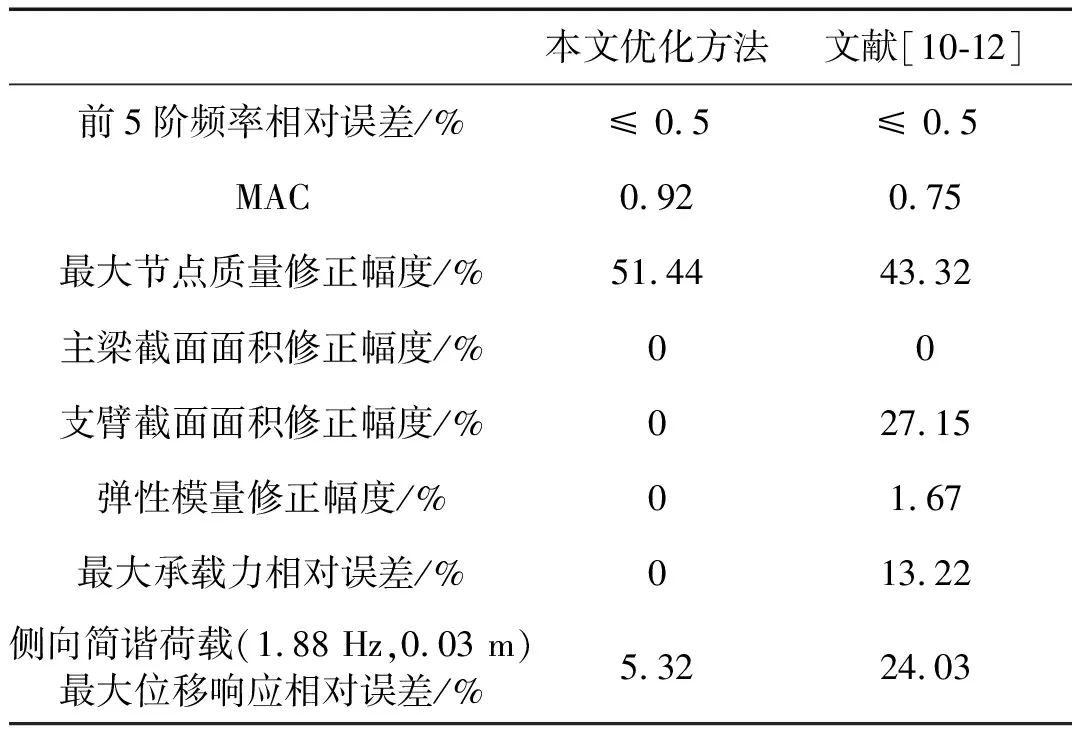
表2 不同優化方法結果分析Tab.2 Calculation results of different optimization

通過與現有文獻中多參數變量優化方法對比表明，在保證低階頻率修正相對誤差小于0.5%的情況下，本文方法僅對節點質量進行修正，其優化模型不改變原有承載力，振型相關性較好，隨機振動位移響應誤差較小。而文獻[10-12]通過靈敏度相關分析選取眾多變量(節點質量、截面尺寸、彈性模量)，盡管滿足了模態頻率的一致性，但極大的改變了原有結構形態，造成結構承載力改變，同時文獻中忽略振型約束條件，導致優化模型與原有結構振型相關性較差，造成了隨機振動過程中，位移響應存在較大誤差。

4 弧形閘門動力模型優化實例

以圖4某水電站深孔閘門1∶20的“全水彈性相似”模型實驗為例，實際最大擋水水頭為93 m，孔口尺寸為4 m×5 m(寬×高)。鋼結構密度為7 850 kg/m3，彈性模量為210 GPa，泊松比為0.25。實驗儀表為：航天工業總公司701所研制的帶壓電式力傳感器的力錘，揚州無線電二廠生產的CA-YD-141型壓電式三向加速度傳感器，2692型電荷放大器及東方振動與噪聲研究所研制的INV206D(M)E型智能信息采集系統。

有限元模型均采用殼單元，劃分單元數為10 661，節點數為9 216，模型如圖5所示。同時考慮到閘門振動屬流體誘發振動，根據Westergaard公式加入流固耦合引起的“附加質量”。本文迭代收斂準則為前五次迭代相對誤差不超過10%，此后不超過5%，優化結果及評價如表3、圖6所示。

圖4 弧形閘門完全水彈性相似模型Fig.4 Physical model of radial gate

圖5 弧形閘門有限元模型Fig.5 Finite element model of radial gate

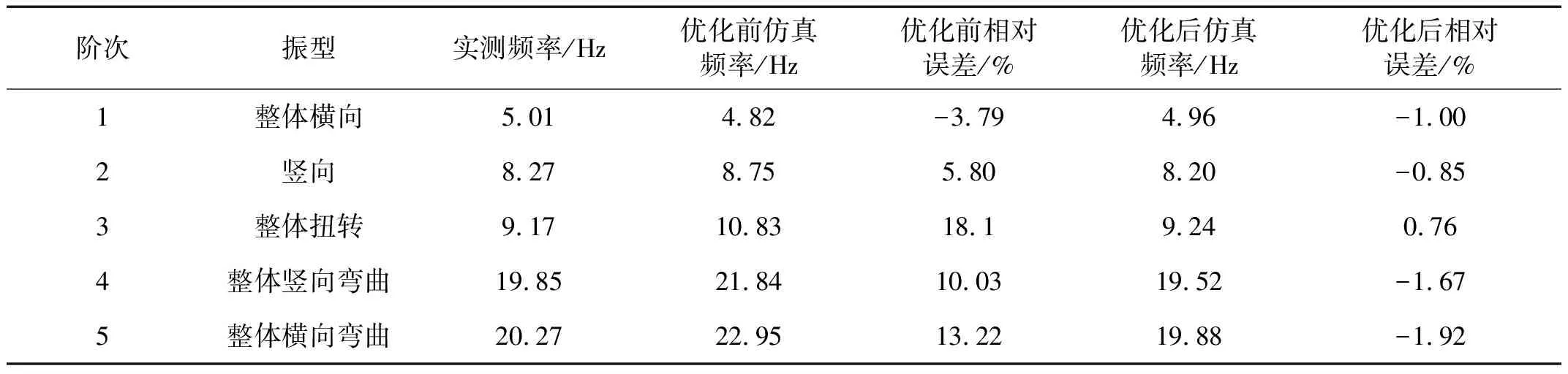
表3 有限元模型計算頻率與實測結果對比Tab.3 Frequencies comparison between the FEM and testing

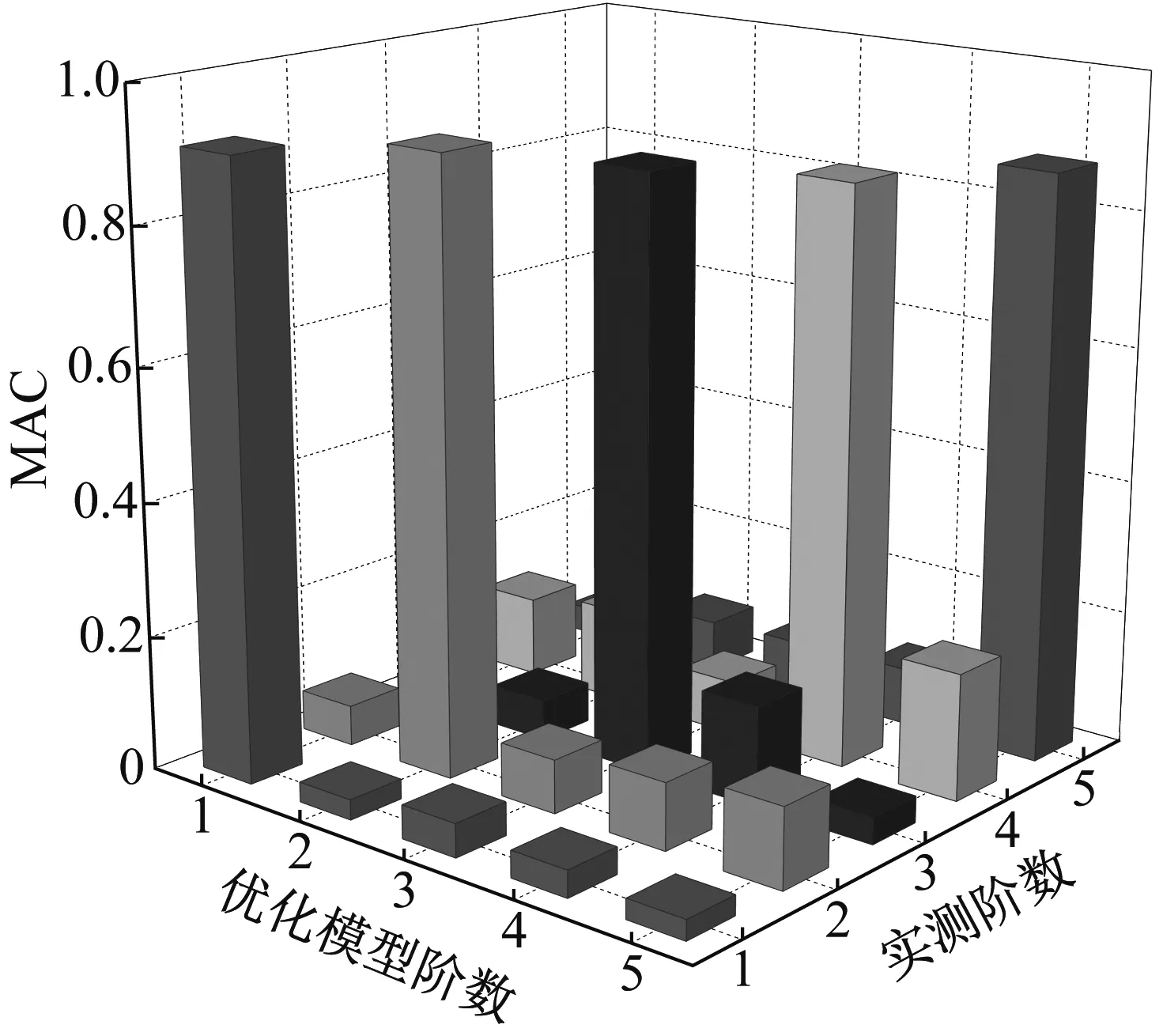
圖6 相關置信因子圖Fig.6 Figure of MAC

從表3可以看出，初始模型的計算結果與實測頻率存在較大誤差，通過特征值靈敏度優化迭代后，誤差滿足收斂預設的誤差范圍。通常MAC對角元素大于0.8，非對角元素小于0.2可以說明振型相關性較好，從圖6可以看出，實測振型與優化后弧形閘門動力模型相關度較好。弧形閘門流激振動過程可由振型疊加法得到，以此判斷本文弧形閘門動力模型可合理模擬流激振動響應。

5 結 論

本文針對弧形閘門有限元模型動力分析過程中存在偏差的問題，提出一種Isight-MSC.Patran/Nastran聯合仿真與特征靈敏度優化相結合的節點質量重分布快速建模方法。通過對弧形閘門主框架有限元模型的攝動檢測，證明了本文方法的有效性，進而與以往參數優化方法進行對比說明了本文在盡可能保證與原有結構幾何、材料性質一致情況下，能夠獲得更為精確的動力有限元分析模型。在此基礎上根據弧形閘門完全水彈性振動實驗數據，利用本文方法建立考慮流固耦合情況下的有限元模型，結果表明，該方法可以較好地用于修正模型動力仿真中存在的誤差，為提高弧形閘門動力設計水平，確定其減振控制策略提供了更精確的動力分析模型。