輔磁同步磁阻電動機低轉矩脈動下轉子結構優化

代希杰，張廣明，鄧 歆

(南京工業大學,南京 211816)

0 引 言

永磁輔助同步磁阻電動機(以下簡稱PMaSynRM)的橫截面幾何形狀如圖1所示，相當于在同步磁阻電機(以下簡稱SynRM)轉子層中插入永磁體，故也可稱內置式永磁同步電動機(IPMSM)。PMaSynRM和SynRM相比于感應電機，有更高的轉矩密度和效率，而PMaSynRM比SynRM轉矩脈動要小得多，因此PMaSynRM在業界越來越廣泛使用,此類型的電機已在文獻[1-3]中作了一些比較。然而，PMaSynRM也有一些固有的缺點，例如電機在高

圖1 PMaSynRM的橫截面

速弱磁區域運行時，永磁體和d軸的大電流產生的磁鏈難以控制[4]。因此，PMaSynRM的設計引起行業和研究者的極大興趣[5-7]。

有研究開始探索如何合理利用和放置永磁材料來獲得高效率、大轉矩且低轉矩脈動的電機。PMaSynRM應運而生，并認為是永磁電機和磁阻電機的最佳替代品[8]。根據轉子上永磁體放置方式的不同，PMaSynRM可分為單層內置、雙層內置、三層內置、軸向疊片內置，其中單層內置式中包含徑向式、切向式、V式、U式[9]。文獻[10-12]中，VagatiA認為SynRM定子齒槽數一定時，當β=α/2(如圖2所示)，位于轉子q軸處的2β相當于在轉子上開的虛槽，此時轉矩脈動最小；在文獻[13]中，Bianchi

圖2 PMaSynRM一個磁極下的幾何結構

N設計的R型模塊：vb1=14.8°，vb2=24.7°；設計的J型模塊：vb1=22.2°，vb2=40.2°；到優化后的“Machaon”型模塊，vb角介于R型和J型之間在達到轉矩脈動較低的同時，轉矩質量也較可觀。

本文主要對轉子中永磁體和磁障位置的放置和形狀進行設計及優化，通過仿真軟件Maxwell得到轉矩及脈動，對比試驗結果，從而得到最優值。最后通過分析等效磁路模型來預測開路氣隙磁通密度分布，并與有限元分析得到的氣隙磁通密度分布相對比，得到誤差在5%以內，檢驗此分析模型下的等效磁路法的正確性。

1 磁體與磁障徑向段選取策略

對永磁體厚度的優化，既要確保q軸電感較小，以增大凸極率，又要避免過多的浪費，降低成本，還要確保厚度太薄后電機在滿載運行時的退磁現象。對永磁體厚度的選擇在文獻[14-15]中有詳細的探討。

從轉矩公式和弱磁控制[16-17]可以看出,d，q軸的電感差值越大，磁阻轉矩值越可觀, 磁場調節代價也越小。因此,磁障徑向寬度設計的主要追求目標是最大限度地增大d，q軸磁阻差，即提高凸極率。其磁障徑向d，q軸尺寸設計如圖2所示，通過β角處的虛槽間距以調整α角，借助Maxwell仿真得出最優轉矩質量與轉矩波動。

由于q軸上存在多層永磁材料(其磁導特性近似于氣隙)，阻礙q軸磁力線通過，使q軸電感由氣隙和永磁體層相疊加而成，因而在氣隙中產生的磁動勢波形如圖3所示，圖中每個柱形對應相應的α角及si間距。

圖3 磁動勢交軸反應

2 參數選取與仿真結果比較

在圖2中，ti(i=1,…,k)為在q軸上第i層永磁體的厚度，lmagnet表示q軸上k層永磁體厚度的總和(lmagnet=t1+…+ti)；si(i=1,…,k)為在q軸上第i層軟磁材料的寬度，liron表示q軸上k層軟磁材料寬度的總和(liron=s1+…+si)；+α表示轉子從q軸處旋轉的機械角；而：

kmq=lmagnet/liron

(1)

(2)

式中：kmq為q軸上總的永磁體厚度與軟磁材料寬度的比值(此比值直接影響著凸極率的大小)；α為轉子內磁障夾角；β為最后層磁障基于α的控制角；p為磁極對數；k為磁障層數，本文取k為3。

在圖3中，可有:

(3)

(4)

Δfi-1=fqi-fqi-1i=2,…,k

(5)

(6)

如圖4所示，d軸上電感在氣隙中產生的磁動勢波形對應的d軸磁動勢間距：

(7)

(8)

(9)

(10)

圖4 磁動勢直軸反應

kmq=0.7時，改變β角而產生的轉矩和轉矩脈動，在圖5、圖6中描繪出來。圖5給出不同β角下的平均轉矩和轉矩脈動峰峰值,由圖5可以知道，在-3°到0區間內，轉矩脈動可以降到最低。圖6為不同角度下的轉矩曲線，可以看到在一個周期40 ms內的轉矩波動狀況,圖6中給出α為13.9°，12.9°，10°，β相應為-3.75°，0，10°的轉矩曲線。

圖5 平均轉矩與

圖6 轉矩曲線(Is=50 A,

3 PMaSynRM空載磁路分析

本節討論PMaSynRM在空載狀態下運行時，電機內整個磁場的分布狀態。圖7顯示PMaSynRM在有限元分析下描繪的磁力線分布。

圖7 有限元分析下的磁力線圖

氣隙橫截面面積可分為3個部分：

Sg1=Sg2=α(Rrotor+g/2)Lstk

(11)

Sg3=(α+β)(Rrotor+g/2)Lstk

(12)

從圖7中的磁通路徑可看出，通過Sg1磁力線φg1由PM1所激勵；通過Sg2磁力線φg2由PM1和PM2所激勵；而通過Sg3磁力線φg3由PM1，PM2和PM3所激勵。并假定Sg2區磁通是由PM1和PM2所在的Δ1=(wm2-wm3)/2區所激勵，Sg1區磁通是由PM1所在的Δ2=(wm1-wm2)/2區所激勵。因此，圖8為一個磁極通過這3個區域所對應的氣隙磁通密度分布曲線和對應電阻Rgi=g/(μ0Sgi)，i為相應的1,2,3區域。

圖7中經過各層磁障的漏磁通φb1，φb2，φb3分別由所在的永磁體PM1，PM2，PM3所激勵，相應的漏磁阻為Rb1，Rb2，Rb3。圖9為PMaSynRM一個磁極單個磁障的截面圖和其等效電路。

圖8 一個磁極下氣隙磁場密度分布曲線

(a) 截面圖

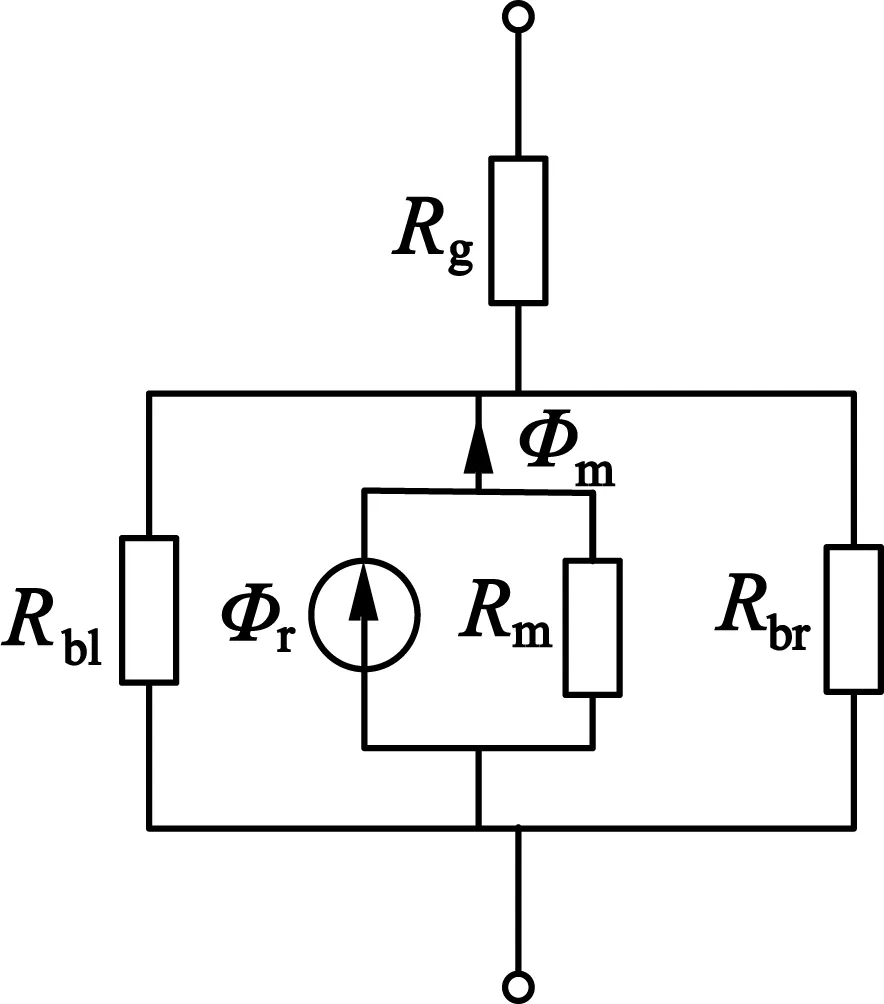
(b) 等效電路

(c) 等效簡化電路

永磁體作為磁通源而產生磁場，形成磁路，而永磁體自身的磁阻Rm與磁源Φr相并聯，并有

Φr=BrwmLstk

(13)

(14)

式中：Br為永磁體剩磁密度；μr為相對磁導率，μr≈1。圖9(b)中永磁體PM的左邊磁障磁阻Rbl和右邊磁障磁阻Rbr在等效電路中相并聯，并聯后的等效磁阻可得出：

(15)

式中：磁障厚度tb與tm近似相等。

圖9(c)為其等效簡化電路，簡化后電路總磁阻：

(16)

由以上分析，可畫出圖7磁路的等效電路圖，如圖10(a)所示。Rs1，Rs2，Rs3和Rrotor分別是磁路經過定子磁軛和轉子磁軛的磁阻，一般情況下，定、轉子磁軛上的磁路沒有充分飽和，與氣隙磁阻Rg1，Rg2和Rg3相比較可以被忽略[11-13]。

(a) 等效電路圖

(b) 簡化電路圖

圖10(b)為其簡化電路，且Uri=ΦriRbmi，i=1，2，3。選取環路φ1～φ3，根據基爾霍夫電壓定律，有：

(17)

由式(17)可以較容易計算出φ1,φ2,φ3的值，進而從圖10(b)中可以得到φg1=φ1-φ2，φg2=φ2-φ3，φg3=φ3，因此通過式(11)、式(12)和φgi=BgiSgi可以相應地計算出Bg1=φg1/Sg1，Bg2=φg2/Sg2，Bg3=φg3/Sg3。

表1給出了PMaSynRM的參數設計。

表1 PMaSynRM設計參數

圖11為在轉子運動90°機械角度下(0～+α)，采用解析法和有限元法得出的氣隙磁通密度分布和對比。有限元法分析時忽略定子開槽的影響，且可以看出轉子內磁障對應處氣隙磁場密度的抑制效果，可以理解為磁障為虛槽的影響，體現在圖中降低處，前提是磁障和轉子邊緣相距得足夠近。圖12為考慮定子槽的實際氣隙磁場密度分布，從圖12中可算出每層磁體對應的Bg1,Bg2,Bg3與圖11中對應的氣隙磁場密度結果近似，驗證了此分析的正確性。

圖11 氣隙磁場密度

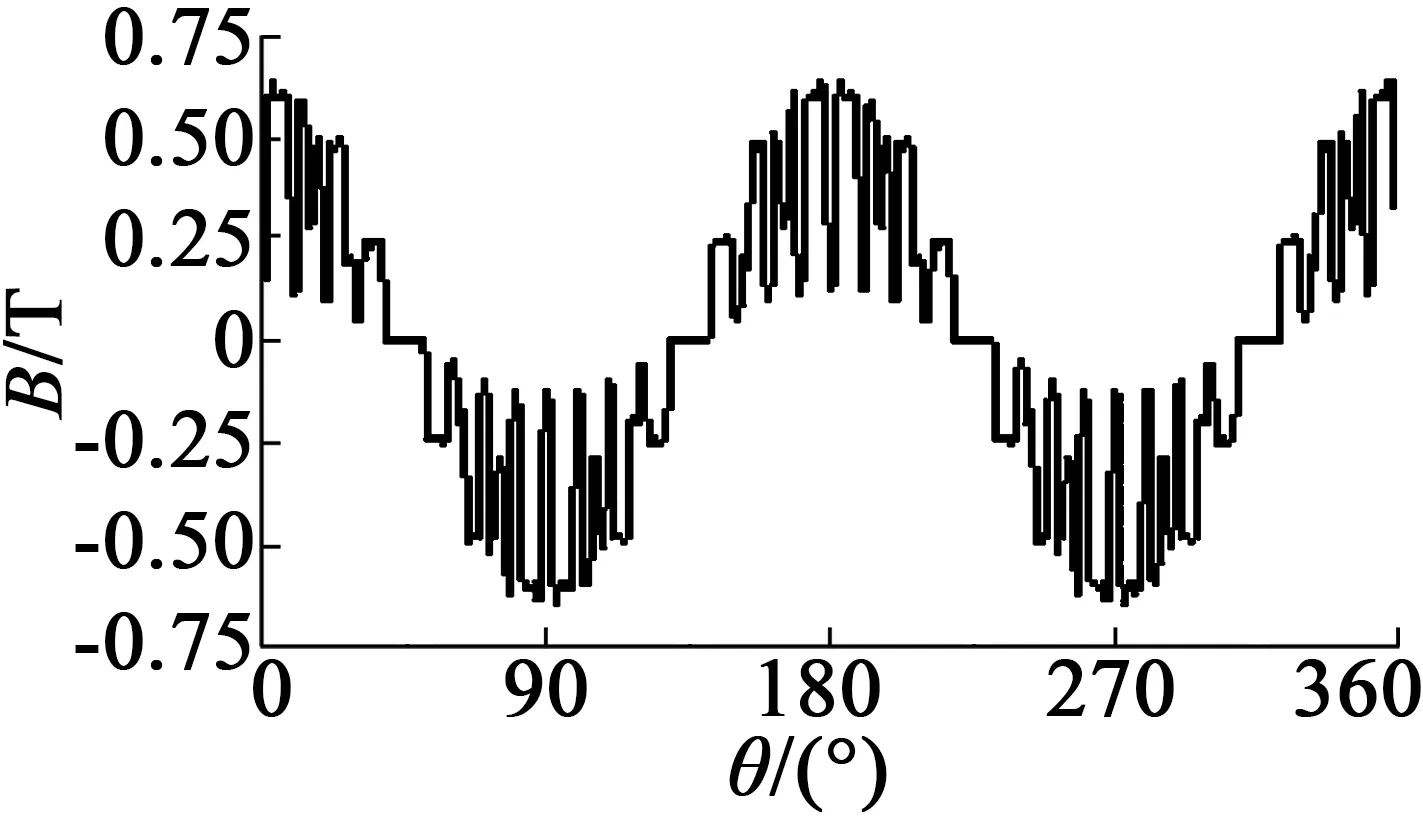
圖12 實際徑向氣隙

4 結 語

本文采用CAD繪圖工具，將所得模型導入Maxwell中仿真，分析了PMaSynRM負載下的轉矩質量與轉矩脈動，并擇以優化。隨后對PMaSynRM空載下的磁路進行分析，采用解析法，通過MATLAB仿真工具與有限元仿真，得出實驗結果相一致，從而驗證該方法的準確性。在目前有關奇異性轉子PMaSynRM的設計與研究資料較少的情況下，本文介紹和改進的設計方法對PMaSynRM的設計和研究有一定的參考作用。