數學建模下的高中數學函數教學探討

楊帆 湖南省懷化市新晃一中 419200

運用數學建模解決高中函數,將數學建模方式納入到函數教學設計中,是一個把實際問題進行抽象,化繁為簡,用數學語言描述問題,進而建立數學模型,解決問題的過程.

一、數學建模是函數教學中的應用

按照新課程對高中函數的要求,是要掌握基本概念和理論知識,并且解決相關應用問題,如,分段函數、二次函數和三角函數.另外要學會將函數和實際相結合,通過函數模型解決現實生活問題,同時建立函數和其他數學知識的聯系.

因此在高中函數教學課堂中教師要根據課程要求,對函數教學進行相應的改進和完善,從實踐角度對函數教學進行不斷優化和革新.

使用數學建模進行高中函數教學就是其中一種比較實用的方法,用建模解決高中函數問題,主要途徑包括利用基本函數模型解決復合函數模型,通過現實背景抽象函數模型,利用換元解決數形結合問題等.利用數學建模進行教學設計還能有效提升教學效率,提升課堂授課質量,更新師生教學觀念,滿足新課程下的課堂教學需求,同時綜合提高學生的創新能力和應用能力.

二、數學建模下的高中函數教學設計具體內容

(一)根據現實生活情境構建函數模型

函數是描述變量之間的一種數學模型,在解決相關應用問題時,利用數學建模,把實際生活情境抽象化,掌握基本的函數模型,利用數學建模方法的基本步驟解決實際問題.而二次函數的實際應用是比較常見的,其描述的是兩個變量的關系,在現實生活中主要是結合圖形解決面積、產量等問題.

例一、某商場購進一批玩具,每個20元,每天銷量是100個,后因為購進成本提升,要對店內玩具進行提價,經過調查發現每提價2元,則日銷量減少10個,如果不考慮其他因素,那么要想使每天的銷售額達到最高,則玩具的價格應當是多少元?

分析:在實際生活中這類問題是很常見的,而用數學思維來思考,這道題考察的是銷售總額和單價的函數關系.那么在課堂授課過程中,教師可以引導學生進行分析,將這類實際應用題抽象為數學函數模型.

模型構建:該題可以構建二次函數模型.假設玩具價格為x元,銷售總額為y元.

X10)=-5(x-40)2+8000

根據二次函數圖象與性質可得當x=40時,銷售額最高,最高收入為8000元.

例二、將生活實際情境抽象為對數函數

對數函數的應用集中體現在放射性物質,銀行利息和細胞分類等方面.

如,要確定古蓮子的年份,需要用到某種放射性物質,已知動植物死亡后,這種放射性物質就不再生產,原有的物質也會自動衰退,經過5730年,原有的放射性物質會衰退到原始量的一半,根據科學家的測量,古蓮子的原始放射性物質含量為m,經過x年后剩余量m1與m的關系滿足:m1=m.e

假設從古蓮子中檢測剩余的放射性物質為原始量的87.9%,那么古蓮子的年份為多少年?

分析:這是一道和考古有關的現實生活情境問題,關于探求古蓮子年份類的題目是十分常見的,在解決這類題的時候要善于分析,教師可以用對數函數的相關概念將這類題目抽象化,通過數學思維和語言來描述這類題,利用對數函數的相關理論知識來分析和解題.

模型構建:對數函數

(二)構建數學模型,換元法解決復合函數

換元法是高中數學中常用的解題方法,在將數學建模納入到高中函數教學中的時候可以將換元法和建模結合起來,尤其是面對復合函數問題,可以將復合函數簡化為簡單函數.教師在講解此類問題時,首先要分析復合函數由哪幾種簡單函數組成,然后對其中一種函數進行換元,構造成簡單函數.

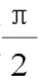
分析:這類題從表面上分析是一道常見的三角函數題,利用三角函數的二倍角公式和誘導公式,可以將函數簡化為:

f(x)= -2sin2x+6sinx+1;

模型構建:可以看出這個函數的變量是三角函數,但形式是二次函數,因此這是一道二次函數和三角函數結合的復合函數,在解題過程中采用換元法,將三角函數轉化為二次函數形式;

令t=sinx,可得f(x)= -2t2+6t+1,其中t∈[-1,1];

利用二次函數的解題模型,考慮定義域的求值范圍,可得:

當t=1.5時,f(x)最大,最大值為5.5;

因為t∈[-1,1];因此當t=1時,f(x)最大,最大值為5.

三、教學反思

筆者在課堂教學中一般采用自主教學法,給學生充分的時間進行討論,首先教師會進行系統講解,每類函數問題應該怎么構建數學建模,然后讓學生進行討論,并總結出有關函數應用題的具體解決方法,從而培養出他們在實際解題過程中舉一反三的能力.

總之,在數學建模下對高中函數教學進行教學設計,需要培養學生的建模意識,了解建模理論,并且不斷深化學生對相關函數知識的理解程度,在課堂教學中采用"探究-討論"的教學方法,更好地推動函數教學中的建模教學模式.