基于二次規劃法的動力定位能力分析研究
張文彬,潘國平,周 興
?
基于二次規劃法的動力定位能力分析研究
張文彬1,潘國平2,周 興3
(1. 湖州新開元碎石有限公司,浙江 313000;2.中船重工集團公司第七0二研究所,江蘇 214082;3. 武漢船用電力推進裝置研究所,武漢 430064)
動力定位能力分析是動力定位系統前期能力評估的重要環節。動力定位能力分析基于沒有角度限制和推力變化率限制的推力分配,通過二分法完成動力定位能力風速包絡曲線的繪制,可將其等同為一個具有限制條件的優化問題。本文采用二次規劃法完成推力優化分配,結合二分法進行動力定位能力分析。仿真結果表明二次規劃法求解推力分配問題及極限風速曲線的有效性。
動力定位能力分析 推力分配 二次規劃
0 引言
動力定位能力曲線是一條極坐標上從0°到360°的封閉包絡曲線,通常采用極限風速曲線,在系統設計初期,能有效地對船舶動力定位系統的定位能力作出評估。極限風速曲線通過船舶能力抵抗的最大環境條件來衡量動力定位系統的定位能力[2]。
包絡曲線上任意一點角度代表環境載荷相對船舶的方向,該方向上船舶保持自身位置與艏向所能抵抗的最大環境條件。最大環境條件的獲得是通過不斷加大作用在船舶上的環境力和力矩,直至推進系統提供的最大有效推力不能與環境載荷平衡為止。環境載荷通常包括有風,浪,流。一般情況下,流速為固定值,風力和浪力成正相關。由推力優化分配計算出的分配結果,往往能最大效度的利用推進器的能力,從而得到極限風速值,本文利用二次規劃方法,簡化推力分配模型,結合二分法,完成極限風速曲線的繪制。
1 二次規劃法求解極限風速曲線原理
在極限風速曲線繪制時,每個風向角可以獨立求解,使用二分法來求解,即先給定一個風速的范圍,用上限風速和下限風速的中間值作為輸入風速進行推力優化分配計算,步驟如圖1所示[3,4]。
其中推力分配模塊用以求解當前風速及風向下,推進系統能發出的最大推力及力矩是否能滿足抵抗環境載荷所需要的要求。環境載荷的計算參考IMCA140[1]。
推力分配問題作為極限風速曲線繪制的重要環節,最終可簡化為求解帶約束條件的優化求解問題,即在滿足推力大小的限制條件下,尋找最優的且能滿足等式約束的推力分配組合。
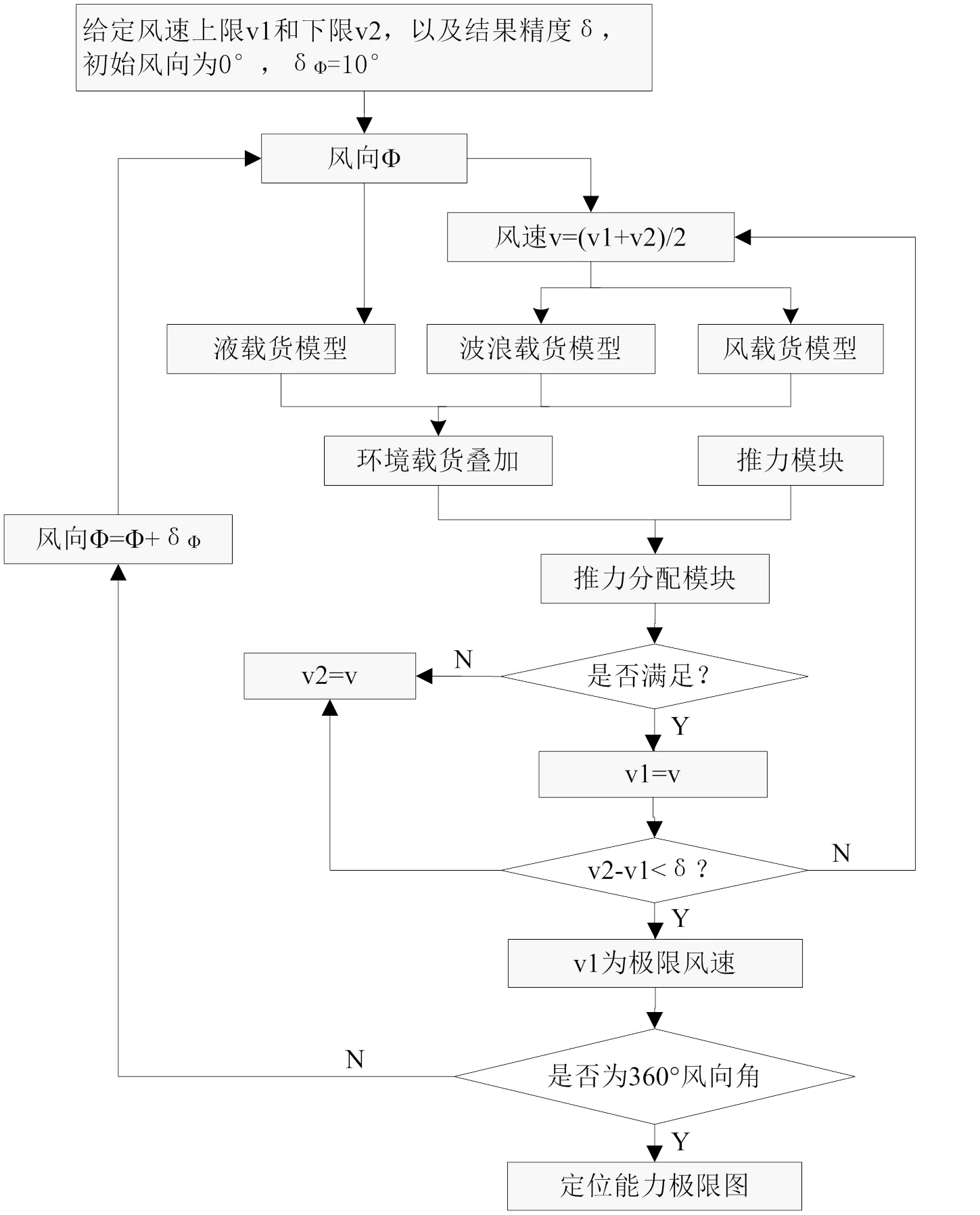
圖1 二分法求解極限風速曲線
2 極限風速曲線求解模型
2.1 環境載荷計算
根據IMCAM140文件的指導準則,動力定位能力曲線計算的環境載荷可由如下公式進行估算:
風載荷的估算公式如下:
其中,A和A為正向和側向風投影面積,C(α)、
C(α)和C(α)是風載荷系數。
流載荷的估算公式如下:
其中,C(α)、C(α)和C(α)是流載荷系數。
波浪平均二階漂移力和力矩缺乏載荷系數,采用的估算公式如下:
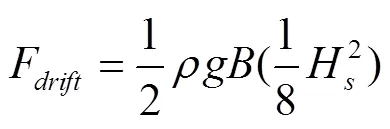
其中H為有義波高。
2.2 推力優化分配模型
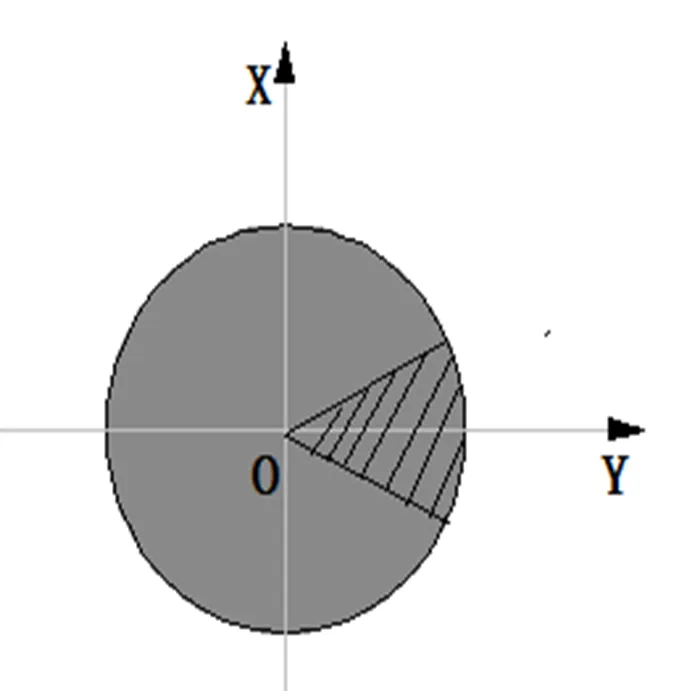
圖2 全回轉推進器推力可行域
動力定位船舶通常配備有全回轉推進器及槽道推進器,全回轉推進器的推力可行域在考慮推力禁區時如圖所示,除去陰影部分,推力可行域為非凸區域,需要將其沿Y軸負向將其分解為兩個凸推力可行域。
二次規劃法求解單目標優化問題時,通常將非線性約束條件,轉換為線性約束,結合二次優化目標進行求解。推力優化分配的目標函數通常設置為推力二次方的函數,非線性的扇形不等式約束可近似為線性約束條件,結合推力和力矩的等式約束條件,可將推力優化分配問題轉換為帶有線性不等式約束的二次規劃問題,方便優化求解。用擴展推力形式表示推進器的推力時,即優化變量為u和u時:此時優化目標函數可表示為:
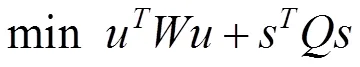
不等式約束條件經過線性化處理之后可表現為如下形式:
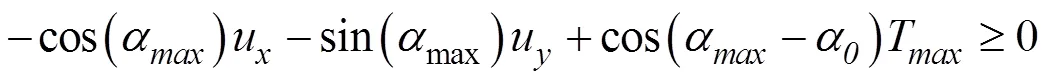
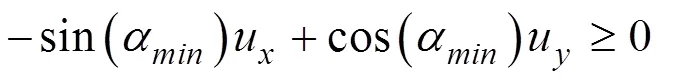
等式約束則可表現為如下形式:
=Bul(5)
3 仿真結果與分析
為了驗證基于二次規劃算法求解極限風速曲線的有效性,利用一條工程船舶參數進行仿真實驗,船體參數如下:
船長:49.8 m;船寬:4.1 m;吃水:2.1 m。
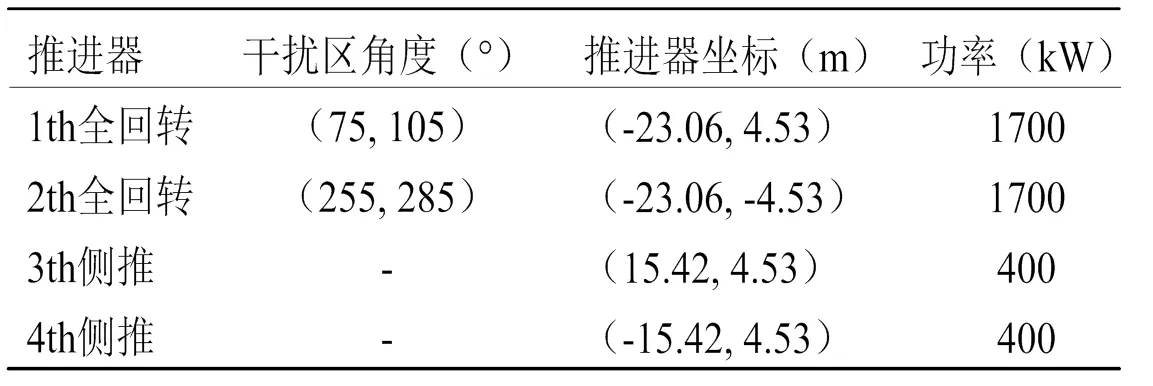
推進器的配置見表1。作業海域流速設定為2 knot/s。
表1 推進器配置
(a)所有推進器可用

(b)損失一個側推
(c)損失一個主推
采用二分法計算時,風速上限設置為50 m/s。仿真中針對本船分別作了四種情況下的計算,分別是推進器全部正常工作。損失一個側推、損失一個主推及損失一個主推和一個側推的情況。本文中的仿真在MATLAB上進行。仿真結果及分析如下:
由圖3中仿真結果中可以看出風速極限曲線在四種情況下,最小極限風速一般產生在60°左右方向。當推進器全部正常工作時,最小極限風速在35 m/s左右;出現一個主推或一個側推損失時,極限風速有所減小,尤其在損失側推時,減小幅度較大;在損失一主一側時,在最小極限風速產生的方向則完全失去抵抗風載荷的能力。仿真結果與實際情況趨勢相符。
4 結束語
本文研究了基于二次規劃優化算法的動力定位能力分析。結合二分法,對推力優化分配模型進行約束線性化處理,利用二次規劃法進行求解。仿真結果說明了二次規劃法求解推力分配問題及極限風速曲線的有效性很高。
[1] IMCA. Specification for DP capability plots[R]. M140,2008.
[2] 邊信黔, 付明玉, 王元慧. 船舶動力定位[M]. 北京: 科學出版社, 2011.
[3] 廣超越. 船舶動力定位系統定位能力分析[D]. 武漢理工大學, 2011.
[4] 許林凱. 動力定位推力分配混合策略研究[D]. 武漢理工大學, 2015.
Analysis Research on Dynamic Positioning Capability Based on Quadratic Programming
Zhang Wenbin1, Pan Guoping2, Zhou Xing3
(1. Huzhou Xinkaiyuan Stone co. LTD, Zhejiang 313000, China; 2. China Shipbuilding Industry Corporation NO.702 Institute, Jiangsu 214082; 3. Wuhan Institute of Marine Electric Propulsion, Wuhan 430064, China)
TP391.9
A
1003-4862(2018)09-0035-04
2018-05-14
張文彬(1968-),男,工程師。研究方向:電氣技術及工程管理。Email: 43721785@qq.com。

