N-gram模型綜述①

尹 陳, 吳 敏

(中國科學技術大學 軟件學院, 合肥 230051)

想象一個人機對話系統, 當計算機在屏幕上顯示:

Please turn your homework …

大部分人認為homework后面應該接to或者是over, 但是不可能是on. 那么計算機處理這個任務時,它根據什么來決定后面接什么？

讓計算機處理自然語言的一個基本問題是為自然語言這種上下文有關的特性建立數學模型——統計語言模型, 它是今天所有自然語言處理任務的基礎. 在20世紀70年代由賈里尼克提出的N-gram模型是最常用的統計語言模型之一, 廣泛用于當今的多種自然語言處理系統中[1]. 目前關于N-gram模型應用的研究有機器翻譯自動評分, 摘要生產系統自動評分, 單詞分類, 文本分類等[2–5], 但是卻沒有對于N-gram模型主要平滑方法的綜合介紹, 所以本文著重介紹了幾種常用的平滑方法.

計算機利用N-gram模型計算出后面每個可能的詞的概率, 并選擇概率最大的詞放到homework后面,N-gram模型還用于計算整個句子在語料庫中出現的概率, 比如下面兩條語句:

S1:I am watching movie now.

S2:watching I am now movie.

N-gram模型會預測句子S1的概率p(S1)大于句子S2的概率p(S2).

在語音識別和手寫識別任務中, 我們需要估算出每個詞w的概率p(w)來識別出帶有噪音的詞或者是模棱兩可的手寫輸入.

在拼寫糾錯系統中, 我們需要找出并糾正句子中拼錯的詞, 比如句子:

S3:Their are so many people.

S4:There are so many people.

在句子S3中計算機認為There被錯拼成了Their了, 因為S4出現的概率p(S4)大于S3出現的概率p(S3), 所以系統會將Their更正為There.

在機器翻譯任務中, 需要確定每個詞序列的概率以找出最正確的翻譯結果:

S5:我今天要去上學.

S6:I today want go on learn.

S7:I today want go to school.

S8:I am going to school today.

由于在英語短語中, go to school出現的概率要比go on learn大以及時間通常放在句尾, 所以計算機認為p(S8)＞p(S7)＞p(S6), 因此S8更有可能是正確的翻譯[6].

N-gram模型常用于估算給定語句在語料庫中出現的概率, 一個N-gram是一個長為N的詞序列. 當N=1時稱為Unigram模型即一元模型, 也叫上下文無關模型;當N=2時稱為bigram模型即二元模型;當N=3時稱為trigram模型即三元模型.

1 N-gram模型

N-gram模型的基本原理是基于馬爾可夫假設, 在訓練N-gram模型時使用最大似然估計模型參數——條件概率.

1.1 基本原理

假設S=w1w2w3…wn表示給定的一條長為n的語句, 其中wi(1≤i≤n)是組成句子S的單詞, 則S出現在語料庫中的概率:

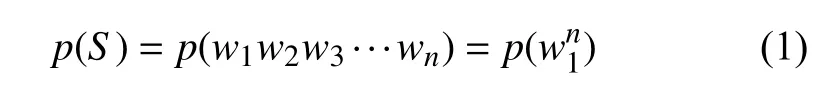
根據鏈式法則和條件概率公式,S出現的概率p(S)等于S中每個單詞wi(1≤i≤n)出現的概率相乘:

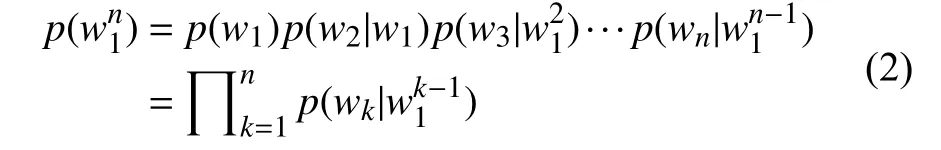
所以為了簡化計算的復雜度, 馬爾可夫提出了馬爾可夫假設:假設任意一個單詞wi出現的概率只和它前面的單詞wi-1有關:

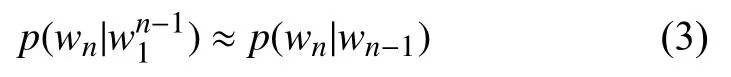
基于馬爾可夫假設得到的是二元模型:

馬爾可夫的假設有不足之處, 比如“happy new year”中“year”其實和“new”與“happy”都有關, 因此柯爾莫果洛夫將馬爾可夫假設推廣到一般形式:假設句子中的每個單詞與其前面N–1個詞有關:

這稱為N–1階馬爾可夫假設[6].

1.2 參數估計

在訓練N-gram模型時, 一個重要的問題就是模型的參數估計即估計條件概率. 以二元模型為例, 需要估計條件概率p(wi|wi-1), 假設c(wi-1)為詞wi-1在訓練語料庫中出現的次數,c(wi-1,wi)為二元組(wi-1,wi)在訓練語料庫中出現的次數, 于是:

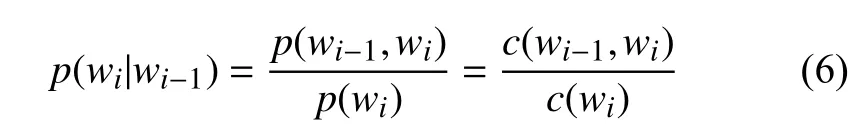
假設一個只有三條語句的語料庫, 每條語句以結束:

則二元模型計算出的部分條件概率如下:

現在我們將在實際中使用N-gram模型, 以布朗語料庫的新聞類別為訓練語料庫, 該語料庫的規模有10054個標識符, 以句子:

S9:I will run for the governor.

為例, 考慮二元模型, 在語料庫中的各項統計數據如表1和表2所示.

表1 S9中單詞在訓練語料庫中的頻數

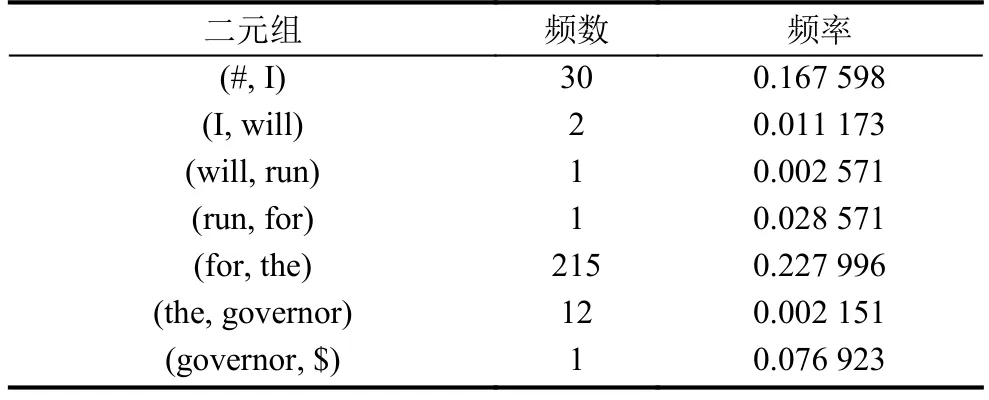
表2 S9中二元組在訓練語料庫中的頻數和頻率

表1和表2中, (#, I)表示S9以I開頭, (governor,$)表示S9以governor結尾, 根據公式(6)計算S9出現的概率, 由于概率值均在0～1之間, 導致多個概率相乘的結果會非常小, 所以我們對最終的概率值取以10為底的對數, 結果是–11.2849(后面概率計算結果均是取對數后的結果).

在實際應用中, 通常使用三元模型的居多, 谷歌公司的翻譯系統則使用四元模型, 這個模型存儲在500臺以上的服務器中.

1.3 零概率問題

假設有如下語句:

S10:Will I run the for governor.

考察一下它出現的概率

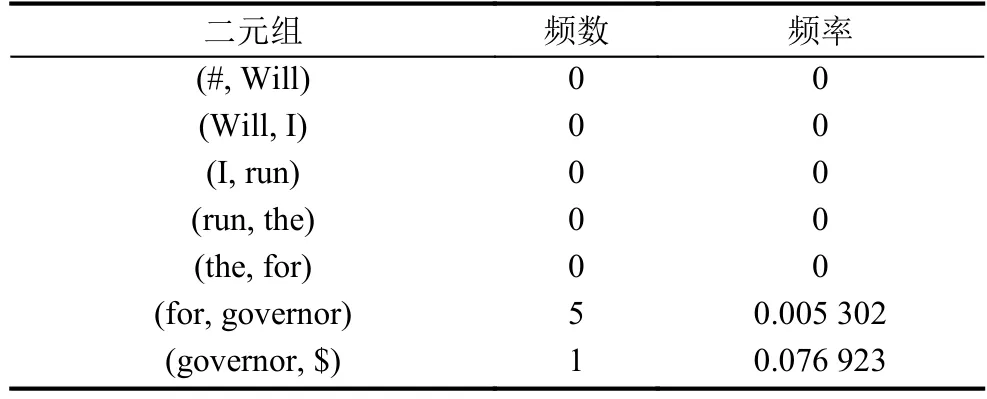
表3 S10中二元組在訓練語料庫中的頻數和頻率

統計時出現了很多頻數為零從而導致頻率為零的結果, 即所謂的零概率問題.

布朗語料庫的新聞類別中使用最頻繁的前50個單詞的頻數變化(包括標點符號)如圖1所示.

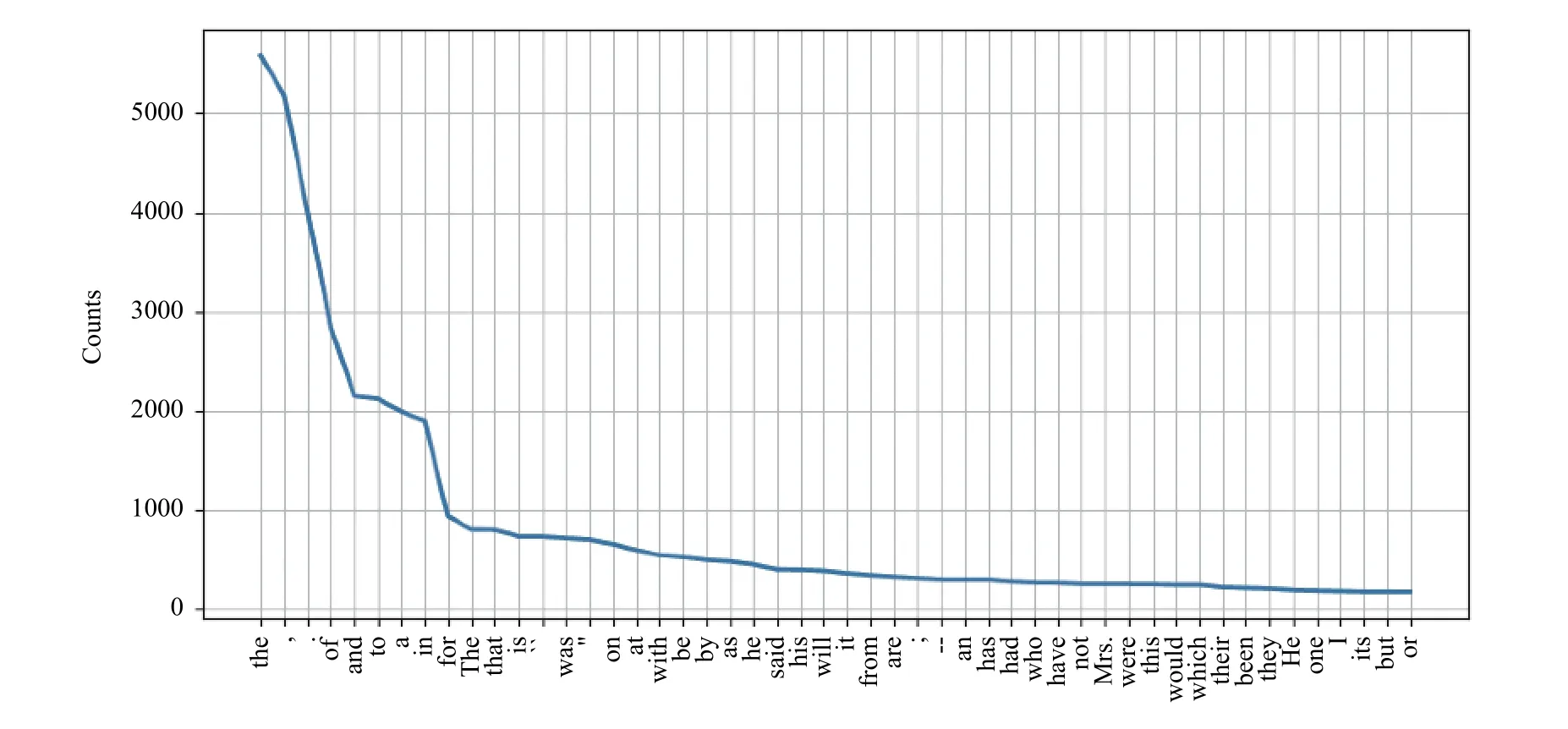
圖1 單詞頻數變化

在該語料庫中只有極少數單詞被經常使用, 而絕大多數單詞很少被使用, 這就是著名的Zipf定律:一個單詞出現的次數與它在頻率表里的排名成反比. 假設在語料庫中出現r次的詞有Nr個, 那么在布朗語料庫的新聞類別中它們之間的關系符合圖2所示的Zipf定律.

詞出現的次數r與詞的數量Nr是反比例關系, 即Nr+1＜Nr. 假設語料庫的規模為M, 未出現的詞的數量是Nr, 則有:

那么出現r次的詞在語料庫中的頻率為r/M, 那么由于語料庫規模的限制, 導致我們統計二元組(Will,I)的頻數為0, 但是事實上Will I這種搭配在英語中很常見, 所以根據這樣的方法估算概率顯然是有誤差的.

圖2 Zipf定律

2 N-gram模型的評價標準

評價一個語言模型的最佳評價方法是把模型應用到實際的產品中, 比較該產品在應用模型前后的性能提高程度, 這稱為外部評價. 但是在實驗中, 由于資源的限制我們無法使用外部評價, 更多的是使用內部評價方法, 即在測試集上使用困惑度作為語言模型的評價準則.

假設測試集W=w1w2w3···wN, 于是在測試集上的困惑度如下:

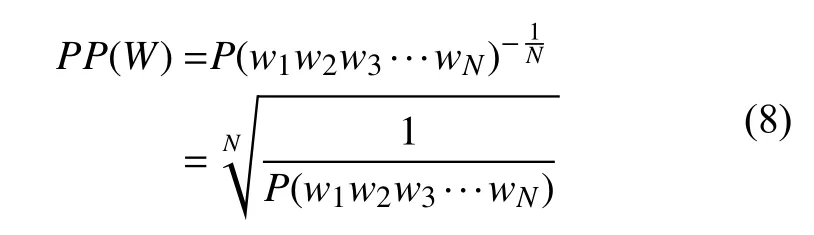
然后使用鏈式法則擴展:

因此, 應用到二元模型就得到:

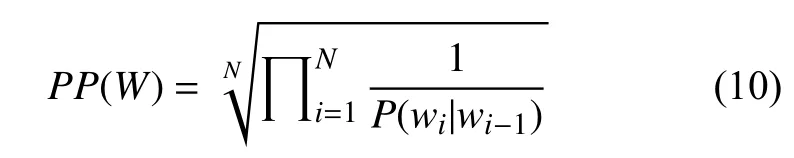
由式(8)可知, 一個詞序列的概率越大, 它的困惑度就越小, 所以語言模型的優化目標就是最小化困惑度.

我們可以從另一個角度來看待困惑度:語言的加權平均分支因子. 語言的分支因子指的是可以跟在任意一個詞后的所有可能的詞的數量. 假設有一個數字識別系統, 用來識別0, 1, 2, ···, 9共10個數字, 假設每個數字出現的概率都是P=1/10, 于是對于任意長為N的數字序列, 這個系統的困惑度是10:

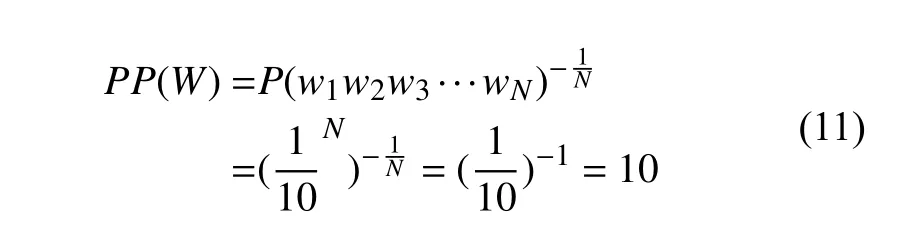
換句話說, 任意的一個數字后面可以接0～9共10個數字中的任意一個數字, 所以這個數字語言的分支因子是10.

我們在布朗語料庫上分別訓練了一元模型, 二元模型和三元模型, 它們的困惑度是

表4 三種N-gram模型的困惑度

由此可見, N-gram模型考慮的上下文越長, 模型的困惑度就越低.

3 平滑

回到前面的零概率問題, 避免零概率問題的方法之一是防止模型把沒看到的事件(如二元組(Will,I))的概率算為零. 所以我們有兩種解決方法, 增大語料庫和改變概率估算方法.

我們加入了布朗語料庫的政府文本類別和學術文本類別, 統計S2中二元組頻數如表5所示.

表5 S2中二元組在擴大后的語料庫中的頻數

在增加了語料庫規模后, 還是沒有解決零概率問題. 所以我們需要平滑:將一部分概率分配給沒看到的事件, 主要的平滑方法有拉普拉斯平滑, 卡茨回退和Kneser-Ney 平滑[7–9].

3.1 拉普拉斯平滑

最簡單的平滑方法是規定所有的詞或詞對至少出現一次, 所以即使是未出現的詞或詞對, 它們的出現次數也被人為設定為1. 這種平滑方法稱為拉普拉斯平滑. 拉普拉斯平滑在現代的N-gram模型中表現不是十分好, 但是它是所有其他平滑方法的基礎, 現在仍然被廣泛應用在文本分類領域中.

假設語料庫規模為M, 語料庫的詞匯表規模為V.對于一元模型來說, 設詞wi的出現次數為ci, 未使用平滑方法之前估算wi的概率為:

應用拉普拉斯平滑后的概率為:

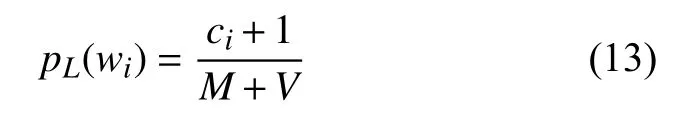
可見拉普拉斯平滑方法將所有的詞計數都增加1,這種平滑方法也叫做Add-one平滑.

為了計算的方便, 通常情況下定義一個調節計數:

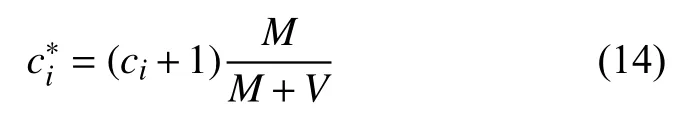
顯然有ci＞, 于是拉普拉斯平滑相當于對原始計數ci打了一個折扣dc:

現在我們將其推廣到二元模型:

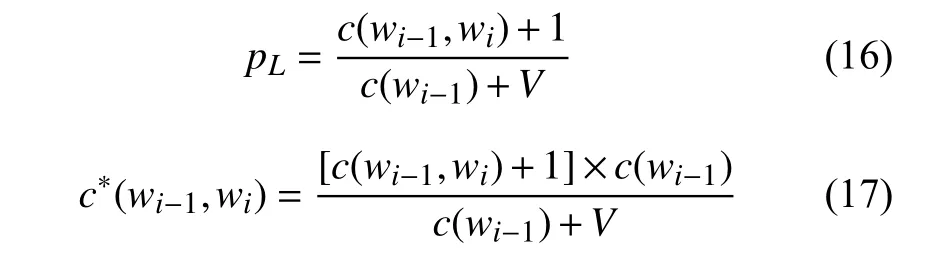
再次統計出S2中二元組在訓練語料庫中的頻率,如表6.

表6 經過Add-one后的S2中二元組的頻率

可以發現零概率問題已經被解決. 但是由于語料庫中未出現的詞或詞對的數目太多, 拉普拉斯平滑導致為它們分配了很大的概率空間, 所以我們可以不加1, 轉而選擇尋找一個小于1的正數k, 此時的概率計算公式為:

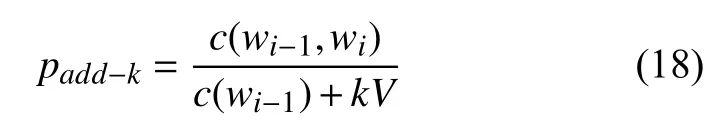
此時叫做Add-k平滑.

3.2 卡茨回退

古德和圖靈提出了一種在統計中相信可靠的統計數據, 而對不可靠的統計數據打折扣的一種概率估計方法:從概率的總量1中分配一個很小的比例給沒有看見的事件, 這樣沒有看見的事件也擁有了很小的概率.

在一個語料庫中出現次數越小的詞, 說明這個詞很少使用, 甚至是不可靠的. 所以當r較小的時候, 統計數據可能不可靠, 于是選取一個閾值σ , 按照古德-圖靈估計重新計算r小于σ 的詞的出現次數:

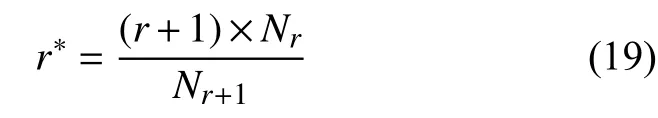
仍然有:

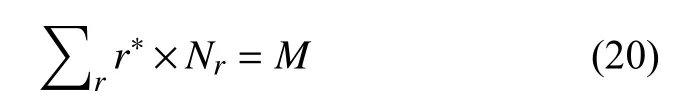
于是當r＞σ時, 對應的詞的概率估計是r/M;當r＜ σ時, 對應的詞的概率估計是r?/M;將1-r/M-r?/M這部分概率分配給沒有看到的詞. 因此二元模型的概率估計公式如下:

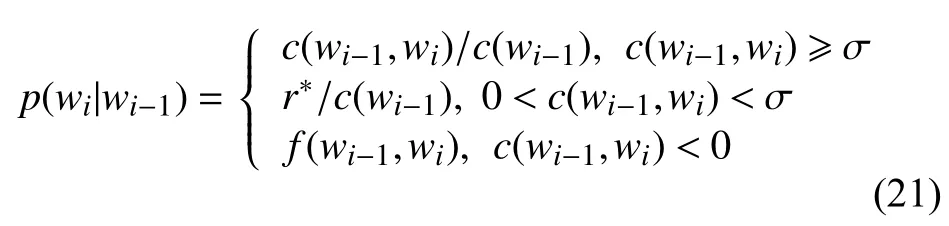
其中,

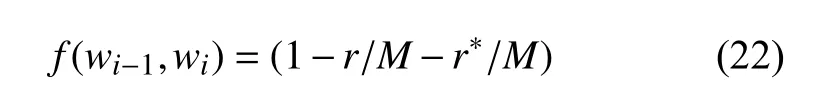
當我們取σ =8時對句子S2的統計數據如表7.

表7 經過卡茨回退后的S2中二元組的頻率

由于一個單詞wi出現的次數比兩個單詞(wi-1,wi)出現的次數要多得多, 所以它的頻率就越接近概率分布. 同理, 兩個單詞 (wi-1,wi)出現的次數要比三個單詞wi-2,wi-1,wi)出現的次數多得多, 所以兩個單詞的頻率比三個單詞的頻率更接近概率分布. 同時, 低階模型的零概率問題要比高階模型輕微, 所以可以使用線性插值的方法, 將高階模型和低階模型做線性組合, 這種方法叫做刪除插值.

比如估算三元模型的概率時, 把一元模型, 二元模型和三元模型結合起來, 每種模型賦予不同的權重1,λ2,λ3, 公式如下:

其中, λ1+λ2+λ3=1. 但是刪除插值的效果略低于卡茨回退, 所以現在很少使用.

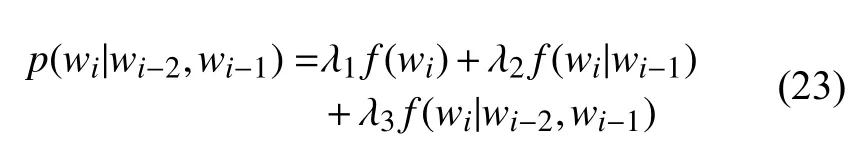
3.3 Kneser-Ney平滑

Kneser-Ney算法是目前使用最為廣泛的, 效果最好的平滑方法. 它的基本思想是絕對折扣.

我們從訓練語料庫中隨機抽取25%的數據作為驗證集, 統計得出在訓練集和驗證集中出現次數在0～9之間的bigram的對比數據如表8.

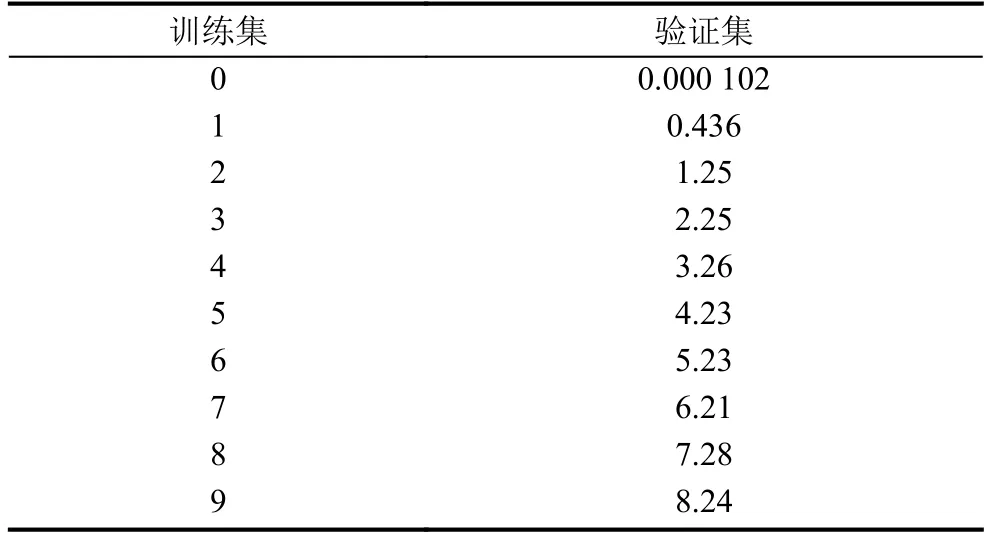
表8 bigram數據對比

可以看出訓練集中的bigram數目在超過1后, 比驗證集中bigram數目約多0.75, 所以對統計出的bigram打一個絕對折扣——總是將這0.75分配給那些沒看見的bigram:

其中,d可以直接設為0.75, λ是一個權重值.

Kneser-Ney平滑對絕對折扣進行了改進, 給定一條語句w1w2···wi-1, 則接下來的詞wi出現的概率:

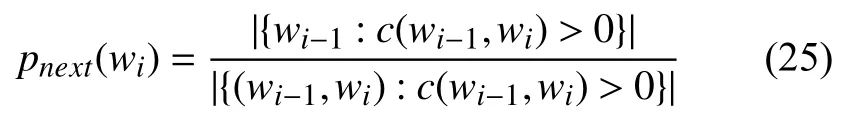
于是Kneser-Ney平滑為:

表示正則化的折扣量[10].

4 總結

N-gram模型在目前的自然語言處理任務中使用最為廣泛的統計語言模型, 它的顯著缺點是無法避免的零概率問題, 有時可以通過增大語料庫規模來解決,但是自然語言是一種動態的語言, 所以從概率計算的方法這一角度來解決零概率問題是在目前是比較科學的. 經過實驗對于規模較小(語料庫規模在3萬以內)的語言處理任務, 卡茨回退平滑方法效果就已經很明顯, 在接下來的研究中, 我們將重點放在優化與綜合利用卡茨回退和Kneser-Ney平滑方法, 利用N-gram模型構建一個提取文章潛在語義的英語作文批改系統.

表9 經過Kneser-Ney后的S2中二元組的頻率