基于量子漫步算法的地震震前異常挖掘①

孔祥增, 江小英, 郭躬德, 李 南, 林 嶺

1(福建師范大學 數學與信息學院, 福州 350117)

2(福建農林大學 計算機與信息學院, 福州 350002)

引言

地震是一種常見的破壞性極大的自然災害,嚴重損害著災區人民的生命和財產安全. 在過去的數十年中,國內外相關領域的研究人員早已開始關注地震前產生的異常, 以期對地震未來的發展趨勢進行預測. 20世紀80年代前蘇聯學者Gorny等[1]首次報道了在中亞及東地中海地區,許多中強震前出現大面積衛星熱紅外輻射增強現象. 其他學者也提出了許多新的震前異常研究成果[2]. NěMEC等[3]使用統計方法研究地震前低頻電磁波數據, 發現在地震前短時間內電磁波的強度會出現異常, 這種與多種因素有關. 張元生等[4]選用靜止衛星紅外遙感亮溫資料證明在大地震發生之前亮溫變化存在明顯的特征周期和振幅以及熱異常分布區域.Kong等[5]使用幾何移動平均鞅算法分析NOAA衛星遙感OLR數據的變化過程, 挖掘汶川地震和蘆山地震前OLR數據的異常. Yeha等[6]采用多個連續GPS基準站建立一個GPS網絡實時監測臺灣南部地殼形變,發現GPS信號在地震發生前很短時間內出現了系統性擾動. Kuo等[7]應用了改進的巖石圈-大氣-電離層(LAI)耦合模型計算日本2011年 Tohoku-Oki 9.0級大地震發生前的電離層總電子含量, 并將計算結果與所報道的TEC觀測結果進行比較, 以研究地震前電離層TEC異常. 文獻[8]中使用渦流場計算和小波變換檢測地震前OLR數據的異常. 文獻[9]中使用模糊神經算法用于檢測震前電磁異常. 文獻[10]中提出了基于誤差和關鍵點的自頂向下分段算法以及基于時間鄰域的局部異常因子的分析方法對地震前兆觀測數據進行異常挖掘. 文獻[11]中提出地面持續增溫是一種相當普遍的臨震前兆增溫異常, 這種前兆異常的時空動態,可實時地反映于衛星熱紅外圖象上. 文獻[12]中提出使用一種非線性過濾器HMMs來提取GPS數據中可能與地震有關的異常信號, 進而達到預測地震的目的. 文獻[13]提出用小波變換來識別并分析數據中的奇異點與地震的關系. Marzocchi等[14]使用貝葉斯估值方法分析地震數據, 構建地震整體預測. 錢國紅[15]利用中國大陸GPS連續觀測站資料,獲取了2011年3月11日日本9.0級地震造成的連續站同震位移, 通過對時間序列分析發現,有明顯同震位移的連續站,震前水平方向的運動速度都有放緩的趨勢. 他們認為這可能是一種地震形變前兆現象. 衛星熱紅外異常是一種臨震預報的新指標. Ouzounov等[16]通過系統地應用衛星數據分析技術, 將衛星數據分析技術應用于大地震后的圖像, 從而驗證TIR異常與已知的地震相關聯. 從上面可以看出,地震發生前會產生很多異常信號, 通過對地震前兆異常的研究與分析, 尋找其中蘊含的地震前兆異常信息對預測地震, 防震減災具有重要意義.

本文的貢獻主要在于:雖然衛星遙感技術已經廣泛地應用于地震科學研究, 但由于熱紅外遙感數據是通過衛星來監測地面的變化, 通常會受到云層等各種因素的影響, 衛星能夠監測到的信號往往比較弱. 缺乏有效的熱紅外遙感數據處理技術來提取地震異常相關信息以及探討震前熱異常內部機制, 導致大多數的熱紅外衛星遙感數據沒有被充分利用. 雖然已經有不少學者開始運用數據挖掘中的異常檢測算法來分析地震異常, 但是通過量子漫步算法來分析震前異常的研究相對較少, 這種算法具有魯棒性, 是一種可行的算法.因此, 為了能夠有效的識別地震熱紅外(射出長波輻射)異常, 本文基于數據挖掘技術的基本原理, 結合Martingale理論[17], 提出一種量子漫步概率算法來識別熱紅外異常特征, 然后在經過一定的信號放大來發現異常. 針對發生在中國比較具有代表性的汶川和蘆山地震, 運用該算法, 對地震前后震中附近OLR數據、P值、CD值進行分析研究. 并且, 通過實驗將該算法擴展到最近十年全球發生的8.0級及以上地震, 驗證該算法的有效性與可靠性. 結果表明, 量子漫步算法是一種具有魯棒性的OLR異常變化識別方法. 同時, 它對將數據挖掘算法運用于地理科學研究領域具有重要的借鑒意義.

1 相關數據

本文研究的對象是發生在中國的2008年5月12日汶川大地震和2013年4月20日蘆山大地震,以及從2005年6月到2014年9月期間全球發生的8級及以上中的16個地震. 具體地震相關數據如表1所示.

2 研究方法

量子漫步作為量子信息領域的一個重要分支, 是經典隨機漫步向量子場景轉變的概括. 量子漫步大致分為離散量子漫步和連續量子漫步兩類. 本文所用的是在直線上的離散量子漫步算法挖掘震前異常. 在直線上的離散量子漫步可以描述為一個維度HP無限但卻可數的希爾伯特空間[18].HP相應的計算基礎是{|n〉|n∈Z}, 其中Z表示整數集. 硬幣空間HC是一個二維的希爾伯特空間, 它的計算基礎是| 0 〉和| 1 〉, 分別對應量子漫步運動的向左走向右走的方向.

量子漫步異常識別方法具體實現步驟如下:

首先, 由硬幣算子UC和轉換算子US組成演化算子U, 且有

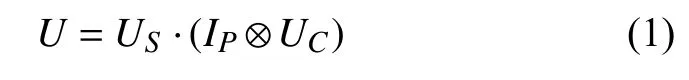
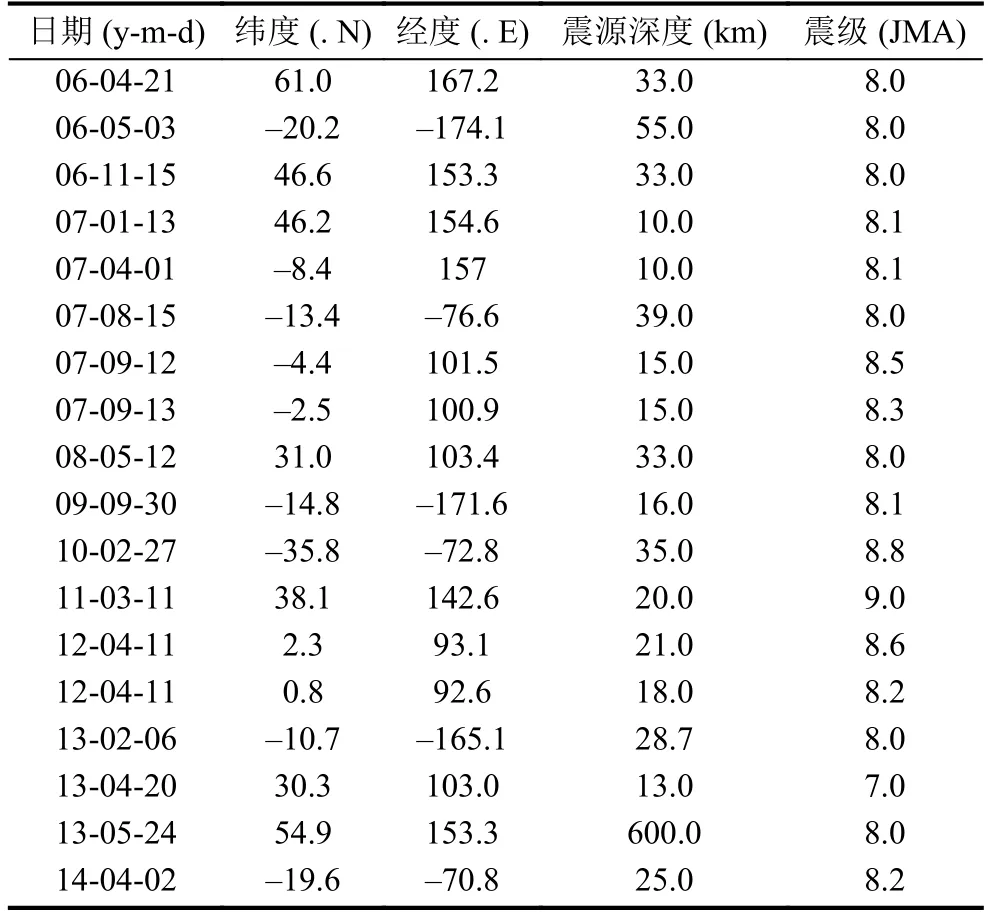
表1 地震相關信息

在每一步中, 硬幣粒子都經過一次哈達瑪變換, 然后, 運動粒子根據硬幣粒子的狀態向對應方向運動. 具體漫步規則如圖1(a)～(c)所示, 從t時刻開始, 粒子在手性“右”(或“左”), 經過哈達瑪變換,粒子現在處于“左”手性態和“右”手性態的相等疊加態, 粒子隨之移動到t+1時刻的狀態.

圖1 離散量子漫步游走規則示意圖

其次, 經過t步之后, 整個量子漫步的狀態為:

其中, | ψ0〉=|P0〉|C0〉, |P0〉表示漫步的初始狀態, |C0〉表示硬幣粒子. 選擇當前監測數據點前ws個數據點, 通過公式(2), 計算每一個數據點的量子漫步概率特征, 分別計算獲得當前數據點根據量子漫步游走的概率分布.

再次, 結合Martingale理論[17],對前兩個步驟獲得的特征序列做如下處理,定義數據點的概率變化程度(CD):

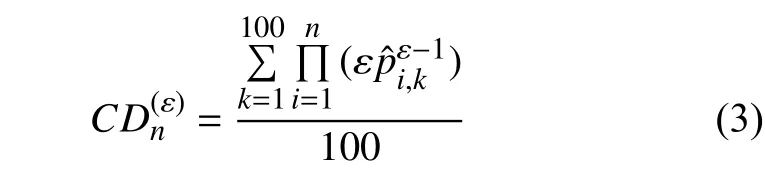
對于無標簽的時間序列數據集Z={z1,···,zi-1}和當前計算的數據點zi. 異常度評分該點跟其他點的區別定義如下:

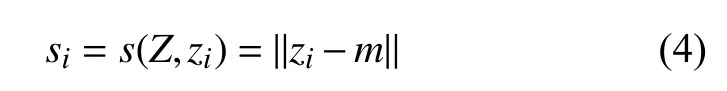
其中, ∥·∥定義的距離度量,m是 集合Z∪{zi}中點的均值.在上面定義的基礎上,我們定義i,k計算如下:

其中, # {}是一個用于返回滿足給定條件的樣本的數量的函數, θi,k為(0,1)范圍內選取的參數,i=1,2,···,n,sj是點zj,j=1,2,···,i的異常度評分,通過等式(4)計算得到Si, 初始化值

通過等式(3)的計算可以看出,CD值越大, 說明地震OLR異常越明顯.

最后, 用上一步計算方法計算每一個數據點的異常度. 為了避免CD值在短時間內出現大波動, 導致結果不可控, 本文算法中設置了一個閾值h作為停止參數,當某一個數據點滿足下面條件時, 說明異常度很大,重新初始化步驟二, 繼續計算剩余點的異常度:

綜上所述, 基于量子漫步算法的異常挖掘算法的流程圖如圖2所示.

3 結果與分析

(1)汶川地震和蘆山地震對應的原始射出長波輻射OLR數據分別如圖3(a)和圖4(a)所示. 量子漫步算法中, 窗口大小ws取值為30–45的每個數, 然后求均值,以降低隨機因素對結果造成的影響. 實驗時, 根據文獻[5], 將閾值h設置為1000. 研究的數據時間周期為一年, 即從發生地震上一年的9月1日到第二年的9月1日. 黑色豎線表示地震發生時間.

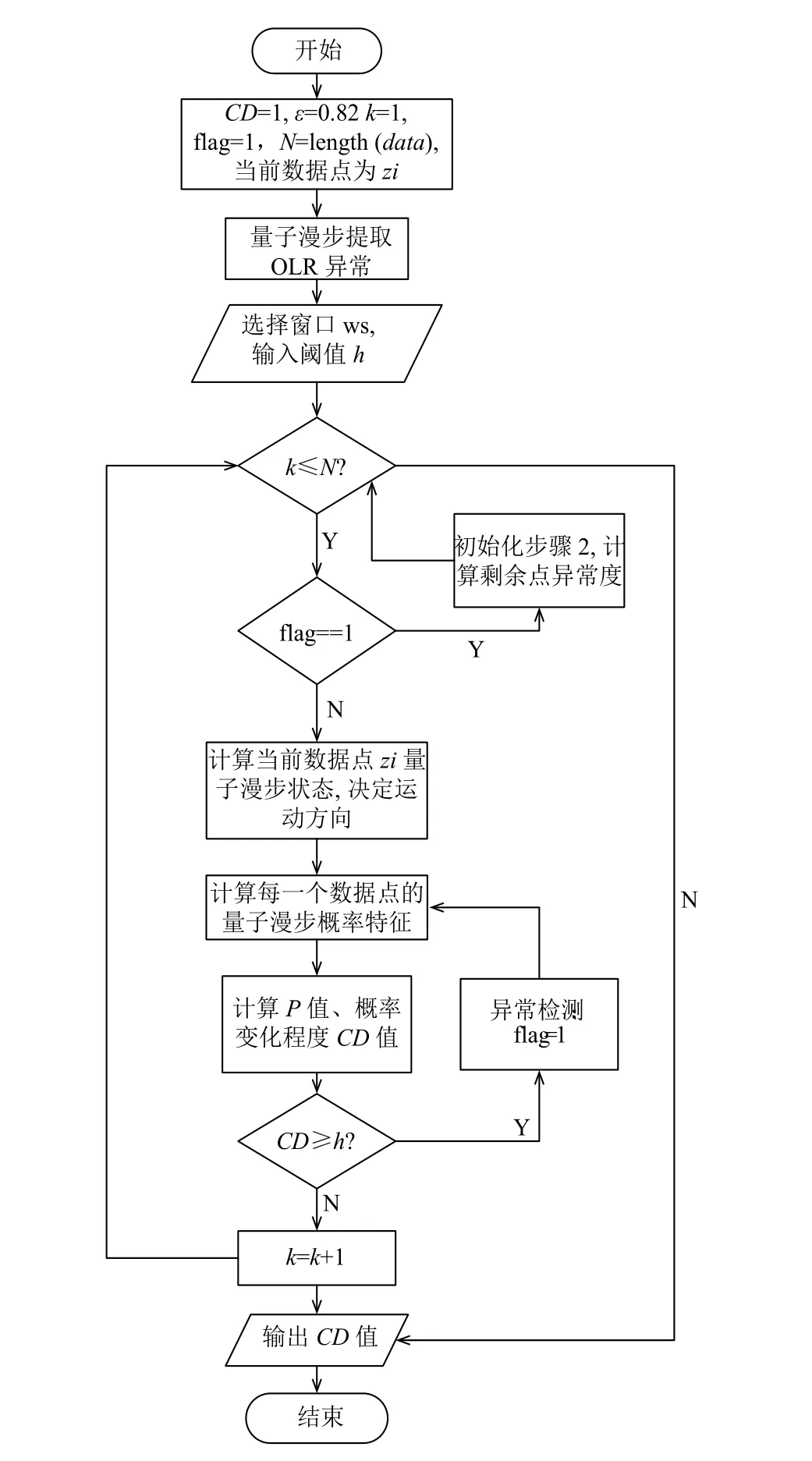
圖2 基于量子漫步算法的異常挖掘流程圖

通過量子漫步算法進行初步處理OLR數據, 計算得到P值, 如圖3(b)和圖4(b)所示. 進一步處理特征序列, 計算數據點的概率變化程度CD, 得到的異常值結果如圖3(c)和圖4(c)所示.

從圖3(c)和圖4(c)可以看出, 在距離地震發生時間較遠的地方,CD值趨近于0, 幾乎沒有任何變化, 說明OLR數據比較穩定. 而臨近地震前后, 兩個地方的CD值均出現了顯著變化, 說明汶川地震和蘆山地震發生前熱紅外異常就已經出現, 且在地震后仍有異常. 這進一步證實了OLR數據中含有大量地震異常信息.

結合圖3(b), 圖3(c), 圖4(b)和圖4(c)可以看出,當地震的P值圖像在短時間內有連續且密集的上下波動的區間內會出現較大的異常值, 即CD值的圖像會在該處出現較大幅度的波峰. 而圖3(a)和圖4(a)的原始OLR數據圖像并未出現明顯的異常趨勢, 這證實了基于量子漫步的異常挖掘算法提取OLR數據異常的有效性.

由于汶川和蘆山兩個地震的震中位置相對較近,成因相似, 因此所提取的異常值CD變化規律比較類似,這從側面說明本文提出的基于量子漫步算法的異常挖掘算法的可靠性.

(2)為了進一步說明本文所提出的基于量子漫步算法的異常挖掘算法的可靠性和有效性, 現在擴展該算法的適用范圍, 將該算法運用于分析2005年6月到2014年9月全球發生的16個8.0級及以上地震的異常數據. 受文章篇幅限制, 本文只展示其中部分地震的實驗結果, 實驗結果如圖5～圖10所示.

通過研究近10年來的時間長度為一年的OLR時間序列, 綜合以上圖5～圖10所示圖像可以看出, 各個地方CD值圖像的變化趨勢有相似的規律, 在距離地震發生時間較遠的地方,CD值趨近于0, 幾乎沒有任何變化, 而在地震前后, 各個地方的CD值均出現了顯著變化, 即臨近地震前后會出現較大異常, 而且越大的地震異常越明顯. 然而, 如果僅從地震區域的原始OLR數據圖像無法直觀地看出是否存在異常. 這也說明本文提出的基于量子漫步算法的異常挖掘算法幾乎適用于所有地震, 具有可靠性和有效性.

(3)為了說明P值和CD值在震前出現異常和地震發生之間的因果關系, 本文針對汶川和蘆山地震分別設計了對比實驗.

首先, 將汶川地震與其他年份(2005年到2017年)汶川地區的P值和CD值圖像進行比較. 實驗結果表明, 在總共12年數據中,CD值大于100, 且小于200的有8個;大于200且小于300的有1個;大于300, 且小于400的有2個;大于400的有1個. 在這12個數據中, 其中有10個異常發生的時間與汶川或其周邊發生的5.0級以上地震發生時間相吻合;出現誤報的僅2個(2007和2016), 即出現異常后, 地震真正發生的概率為83.3%, 誤報率為16.7%.

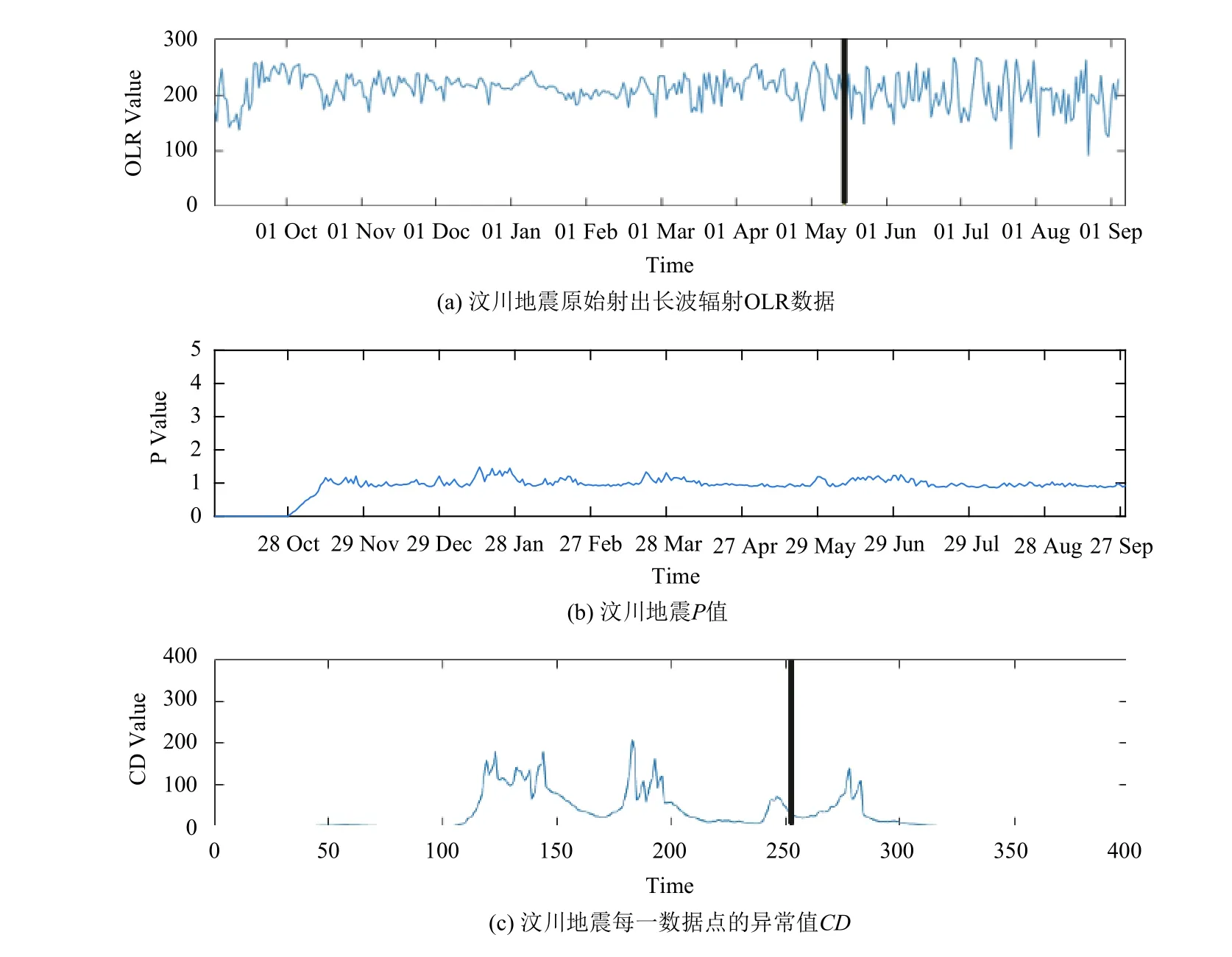
圖3 汶川地震原始OLR數據、P值和異常值CD(2008-05-12)

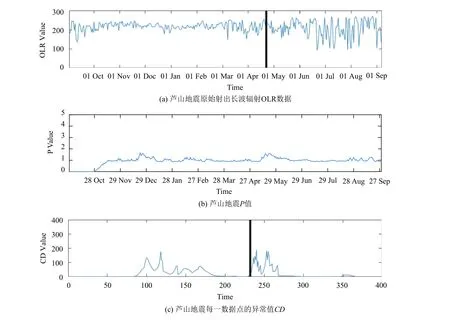
圖4 蘆山地震原始OLR數據、P值和異常值CD(2013-04-20)

圖5 秘魯中部海岸附近地震異常值CD值(2007-08-15)

圖6 印尼蘇門答臘南部海中地震異常值CD值 (2007-09-12)

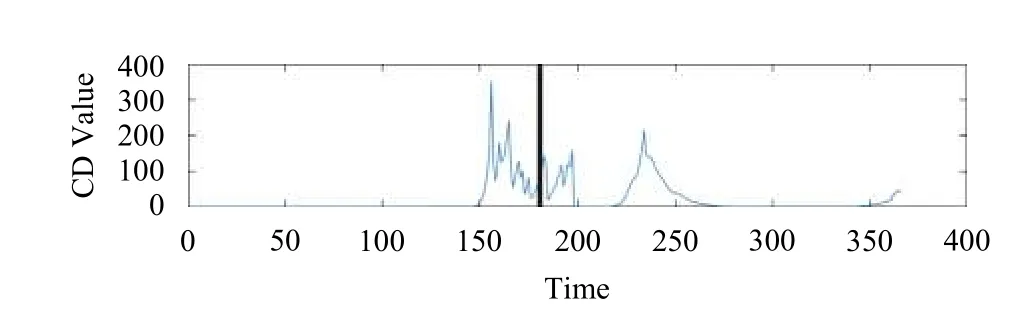
圖7 智利比奧比奧省地震異常值CD值 (2010-02-27)

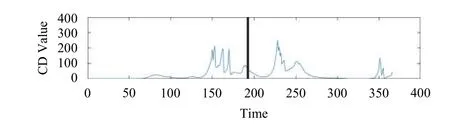
圖8 日本本州東海岸附近海域地震異常值CD值 (2011-03-11)

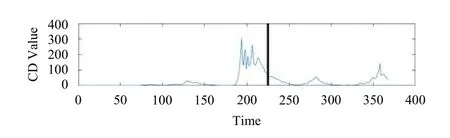
圖9 蘇門答臘北部附近海域地震異常值CD值 (2012-04-11)

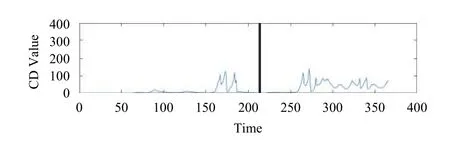
圖10 智利北部沿海岸近海地震異常值CD值 (2014-04-02)

其次, 將蘆山地震與其他年份(2005年到2017年)蘆山地區的P值和CD值圖像進行比較. 實驗結果表明, 在總共12年數據中,CD值大于100, 且小于200的7個;大于200且小于300的有2個;大于300, 且小于400的有2個;大于400的有1個. 在這12個數據中, 其中有10個異常發生的時間與汶川或其周邊發生的5.0級以上地震發生時間相吻合;出現誤報的僅2個(2007和2016), 即出現異常后, 地震真正發生的概率為83.3%, 誤報率為16.7%.

汶川和蘆山2007年都出現大于100, 且小于200的異常, 及2016年都出現大于200且小于300, 筆者猜測可能是由于氣候、溫度或人為活動等原因引起的異常.

(4)為了說明本文提出的算法的優越性, 本文通過實驗, 比較本文提出的基于量子漫步算法的異常挖掘算法與經典隨機漫步算法提取地震異常特征的方法.結果如下圖所示. 其中, 實線曲線(圖中左曲線)為100步量子漫步概率分布, 虛線曲線(圖中右曲線)為隨機漫步概率分布.

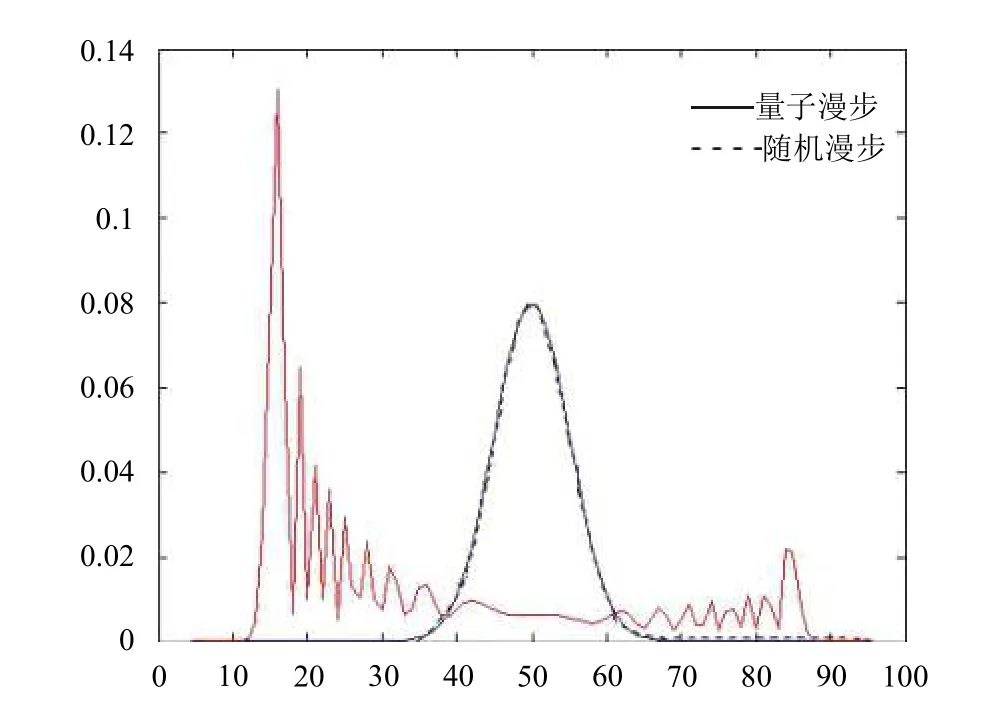
圖11 量子漫步與經典隨機漫步概率模型對比

從圖11中可以看出, 由于硬幣和粒子的量子干涉效應, 在多步以后, 量子漫步算法展現出比經典隨機漫步更好的一些性質. 在執行N步之后, 與經典隨機漫步不同, 離散量子漫步的概率分布并不是高斯分布, 它的分布偏向左邊, 比經典隨機漫步收斂性快, 顯然本文提出的基于量子漫步算法的異常挖掘算法更具有優勢.

4 結束語

本文結合Martingale理論, 提出了一種基于量子漫步算法的震前異常挖掘算法, 并運用該算法分析汶川和蘆山兩個地震的地震前后, 震中附近OLR數據發生的顯著異常變化, 挖掘有用的震前異常信息. 從結果中可以看出, 即使原始OLR數值沒有明顯異常, 在地震前后一段時間內其對應的CD值也會出現較大的變化. 相對于其他傳統的算法, 使用量子漫步算法計算的CD值的變化更能客觀形象地刻畫出地震前后數據的異常程度.CD值越大, 則表明當前數據點的異常變化越大. 這不僅進一步證實了OLR數據中蘊含著震前異常信息, 也為使用量子漫步算法分析OLR數據, 計算CD值預測地震提供了很大的可能. 為了進一步驗證該算法的有效性和可靠性, 本文應用該算法分析近10年左右的全球8.0級地震的OLR, 挖掘地震異常, 結果可觀, 擴展了該算法的適用范圍. 然而, 基于目前的數據量和研究水平, 應用該算法研究地震異常取得的成果很少, 使用量子漫步算法預測地震仍任重道遠. 本文提出的基于量子漫步算法的異常挖掘算法所對應的CD值的異常已經找出了一些初步規律, 但還需要收集更多的地震數據, 進行更完善的實驗進一步挖掘CD值的變化程度與地震相關參數(震源深度、震級、GPS等)之間的關聯性問題, 這也是本文下一步的研究方向.