結(jié)合SIFT和Delaunay三角網(wǎng)的遙感圖像配準(zhǔn)算法①

祁 曦, 陳志云

(華東師范大學(xué) 計(jì)算機(jī)科學(xué)與軟件工程學(xué)院, 上海 200062)

隨著航空航天技術(shù)的不斷進(jìn)步和發(fā)展, 遙感影像不斷向多時(shí)相、多角度及多分辨率方向發(fā)展[1]. 越來越多的科研人員開始對(duì)高分辨率遙感影像數(shù)據(jù)處理進(jìn)行研究[2]. 而遙感影像快速配準(zhǔn)就是這些處理中的關(guān)鍵一步. 遙感圖像是由不同類型的傳感器或從不同角度、不同時(shí)間對(duì)同一場(chǎng)景拍攝形成的, 所以遙感圖像之間會(huì)存在幾何變形, 給遙感圖像處理帶來一定的困難. 圖像配準(zhǔn)就是在對(duì)各類遙感數(shù)據(jù)進(jìn)行處理之前, 先對(duì)兩幅或多幅不同類型的圖像進(jìn)行空間幾何變換, 使得圖像中代表同一位置的對(duì)應(yīng)區(qū)域映射到相同坐標(biāo)下, 而后進(jìn)行匹配或疊加.

目前主要有兩類圖像配準(zhǔn)方法:一類是基于灰度的配準(zhǔn)方法, 另一類是基于特征的配準(zhǔn)方法[3]. 基于灰度的配準(zhǔn)方法主要是比較兩幅圖像的灰度相似性, 找出相似度高的區(qū)域[4]. 該方法對(duì)圖像灰度的依賴程度很高, 運(yùn)算量比較大, 對(duì)圖像灰度差異大、圖像旋轉(zhuǎn)、圖像噪聲等情況的處理效果不佳[5]. 代表方法有最大互信息法[6]、傅里葉變換[7]等. 基于特征的圖像配準(zhǔn)方法是匹配兩幅圖像中的共性顯著點(diǎn), 它大大地降低了計(jì)算量, 且由于只關(guān)注圖像的局部, 所以對(duì)圖像的灰度變化、遮擋都有較好的不變性[8]. 該方法一般選取遙感影像的點(diǎn)、線、區(qū)域等特征, 而其中特征點(diǎn)的提取相對(duì)于線、區(qū)域特征來說, 既可以保證圖像的信息量, 又能降低自身的數(shù)據(jù)量, 且提取容易, 不易受光照、尺度、旋轉(zhuǎn)等圖像變化的影響[9]. 因此基于點(diǎn)特征的方法已成為國(guó)內(nèi)外學(xué)者的研究重點(diǎn). 常用的點(diǎn)特征提取算子有SIFT 算子[10]、Moravec 算子[11]、Harris算子[12]、SURF算子[13]、SUSAN算子[14]等. 其中公認(rèn)最好的點(diǎn)特征提取算子是Lowe于1999年提出并于2004年改善形成的SIFT算子[10]. 相比于其他算子, SIFT算子具有較好的亮度、尺度、旋轉(zhuǎn)不變性, 且對(duì)仿射變換、視角變化、噪聲保持一定的穩(wěn)定性. 但是SIFT算法也有計(jì)算量大、實(shí)時(shí)性差、存在誤配點(diǎn)等問題. 樊東昊等人[15]針對(duì)SIFT算法提取的特征點(diǎn)數(shù)目量大且正確匹配點(diǎn)率不高的問題, 提出了一種基于區(qū)域選擇和SIFT的配準(zhǔn)算法, 避免提取冗余特征點(diǎn), 提高正確匹配率且加快配準(zhǔn)速度. 冷成財(cái)?shù)热薣8]針對(duì)基于SIFT算法的遙感影像配準(zhǔn)過程中產(chǎn)生誤配點(diǎn)且遺漏正確匹配點(diǎn)的問題, 提出了一種改進(jìn)的SIFT配準(zhǔn)算法, 即SODCSIFT算法, 提高正確匹配點(diǎn)對(duì)數(shù)量且提升配準(zhǔn)精度. 李孚煜等人[16]則對(duì)基于SIFT的遙感圖像配準(zhǔn)算法進(jìn)行了總結(jié)概述, 并對(duì)各類算法的優(yōu)缺點(diǎn)進(jìn)行了詳述.

對(duì)高分辨率遙感影像來說, 地物細(xì)節(jié)信息更加豐富, 因此易受拍攝角度、時(shí)相等影響, 比如建筑物等,在傳感器從不同角度拍攝時(shí), 該物體形狀、位置以及陰影區(qū)域等會(huì)發(fā)生不同程度的變化. 由于建筑物的高度變化和陰影區(qū)域的不同, 會(huì)影響特征點(diǎn)的準(zhǔn)確提取和有效匹配, 容易出現(xiàn)誤匹配點(diǎn), 降低圖像的配準(zhǔn)精度[17].同時(shí)為了消除高分辨率影像中的局部幾何變形, 也需要提取恰當(dāng)數(shù)量且均勻分布的特征點(diǎn). 馬旭燕等人[18]針對(duì)高分辨遙感影像中控制點(diǎn)數(shù)目多且分布不均的問題, 提出了SIFT和MSER(極大穩(wěn)定區(qū)域)結(jié)合圖像分塊的配準(zhǔn)算法, 剔除冗余特征點(diǎn)且改善特征點(diǎn)分布的均勻性. 程國(guó)華等人[19]針對(duì)遙感影像本身匹配方法單一且特征點(diǎn)分布不均的問題, 在改進(jìn)Harris算子的基礎(chǔ)上, 結(jié)合分塊迭代剔除策略和小三角形面元TIN, 完成了影像配準(zhǔn).

針對(duì)高分辨率遙感圖像數(shù)據(jù)量大且易出現(xiàn)誤配點(diǎn)的問題, 本文提出了一種基于SIFT和Delaunay三角網(wǎng)的高分辨率遙感圖像配準(zhǔn)方法. 下文首先介紹了SIFT算法、圖像分塊和Delaunay三角剖分的原理, 然后描述了高分辨率遙感圖像配準(zhǔn)改進(jìn)算法的具體步驟,之后對(duì)配準(zhǔn)實(shí)驗(yàn)結(jié)果進(jìn)行分析并得出結(jié)論, 最后對(duì)本文算法進(jìn)行總結(jié)和展望.

1 相關(guān)術(shù)語

1.1 SIFT配準(zhǔn)原理

SITF算法是由David G. Lowe于1999年提出, 并在2004年加以完善. Lowe將尺度的概念引入到SIFT算法中, 利用SIFT方法檢測(cè)圖像特征點(diǎn)的實(shí)質(zhì)就是在不同尺度空間上查找特征點(diǎn), 這些特征點(diǎn)對(duì)應(yīng)的就是不同尺寸的地物[17]. 而在高分辨影像中, 往往就是較小尺寸的地物會(huì)容易發(fā)生變化, 如房屋、汽車等等, 因此為了減少這些小尺寸地物對(duì)特征點(diǎn)提取的影響, 那么就要分尺寸的對(duì)圖像中的地物進(jìn)行分析.SIFT配準(zhǔn)方法主要分為四步:尺度空間的建立, 尺度空間中提取關(guān)鍵點(diǎn), 生成特征點(diǎn)描述子, 特征點(diǎn)匹配.

(1) 尺度空間的構(gòu)建:SIFT算法用函數(shù)L(x,y,σ)來表示圖像的尺度空間, 用函數(shù)I(x,y)表示遙感圖像, 則尺度空間就是由圖像I(x,y)和高斯函數(shù)G(x,y,σ)卷積生成的, 公式為:

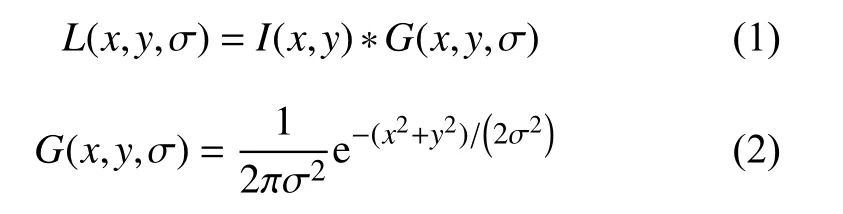
其中, *指的是在x方向和y方向上進(jìn)行卷積操作, σ表示尺度空間坐標(biāo).

為了檢測(cè)穩(wěn)定特征點(diǎn)的位置, SIFT算法用DOG尺度空間來代替LOG尺度函數(shù). 通過對(duì)兩幅相鄰高斯尺度空間圖像相減, 得到DOG尺度空間, 該尺度空間的計(jì)算公式如下:

(2) 尺度空間中提取特征點(diǎn):尺度空間中的所有檢測(cè)點(diǎn)都與其同尺度相鄰的8個(gè)點(diǎn)和上下尺度各相鄰的9個(gè)點(diǎn)進(jìn)行比較, 只保留局部極值點(diǎn). 之后去除其中不好的關(guān)鍵點(diǎn), 通過子像元插值和剔除對(duì)比度低的點(diǎn)以及不穩(wěn)定的邊緣響應(yīng)點(diǎn)來對(duì)精化檢測(cè)到的關(guān)鍵點(diǎn).

(3) 生成特征點(diǎn)描述子:在以關(guān)鍵點(diǎn)為中心的鄰域窗口內(nèi)采樣, 計(jì)算鄰域內(nèi)各像元的梯度幅值和梯度方向, 并用梯度方向直方圖來統(tǒng)計(jì)鄰域內(nèi)像元的梯度方向, 則關(guān)鍵點(diǎn)的主方向就是直方圖的峰值. 之后將坐標(biāo)軸旋轉(zhuǎn)為特征點(diǎn)的方向, 以確保旋轉(zhuǎn)不變性, 然后對(duì)特征點(diǎn)周圍區(qū)域進(jìn)行分塊, 分為 4 ×4個(gè)子區(qū)域, 對(duì)每個(gè)塊內(nèi)的梯度方向進(jìn)行統(tǒng)計(jì), 得到8個(gè)方向的梯度方向直方圖, 最終形成128維的SIFT特征向量.

(4) 特征點(diǎn)匹配:使用歐氏距離來判斷兩幅圖像特征點(diǎn)的相似性. 在匹配過程中, SIFT算法使用的是Kdtree算法, 即找出待配準(zhǔn)圖像中與參考圖像特征點(diǎn)A距離最近的點(diǎn)B和距離次近的點(diǎn)C, 將最近鄰和次近鄰距離相比, 若比值小于給定的閾值, 則認(rèn)為匹配正確, 特征點(diǎn)A與B是一對(duì)匹配點(diǎn).

1.2 圖像分塊策略

在提取特征點(diǎn)之前對(duì)圖像進(jìn)行分塊處理, 有助于改善特征點(diǎn)提取的均勻性, 對(duì)圖像進(jìn)行分塊有兩種方式:

(1) 第一種方式是預(yù)先設(shè)定圖像塊的邊長(zhǎng), 然后對(duì)整幅圖像分塊. 適用于塊數(shù)未知的情況.

(2) 第二種方式是預(yù)先設(shè)定好劃分的塊數(shù), 根據(jù)塊數(shù)來對(duì)整幅圖像進(jìn)行分塊. 通常可劃分 2 ×2、4×4 8×8等.

本文采用的就是第一種方式, 定義劃分的子塊圖像大小為n1×n2, 而這些劃分的子塊圖像之間有一小部分是重疊的, 因?yàn)镾IFT沒有辦法提取圖像邊緣的特征點(diǎn), 重疊區(qū)域的寬度定義為oval.

1.3 Delaunay三角形相似函數(shù)

現(xiàn)在的三角形剖分技術(shù)已日趨成熟, 因?yàn)槠錁?gòu)建的三角網(wǎng)靈活性大且能較好逼近邊界, 所以廣泛應(yīng)用于測(cè)繪學(xué)、地質(zhì)學(xué)、地理學(xué)和圖像學(xué)等領(lǐng)域中.Delaunay三角形剖分就是其中一項(xiàng)比較重要的三角形剖分技術(shù)[20]. Delaunay三角形剖分有最大化最小角和空外接圓兩個(gè)特性, 可以有效的避免常規(guī)三角剖分所帶來的病態(tài)三角形的問題.

三角網(wǎng)的構(gòu)建一般有三個(gè)算法:分治算法、三角形生長(zhǎng)法和逐點(diǎn)插入算法. 由于三角網(wǎng)生長(zhǎng)法搜索效率低, 不適合海量數(shù)據(jù)的搜索建網(wǎng), 分治算法效率很高但會(huì)占用大量?jī)?nèi)存, 而逐點(diǎn)插入算法實(shí)現(xiàn)簡(jiǎn)單且占用內(nèi)存較少, 因此成為本文構(gòu)建三角網(wǎng)的首選算法[20].

構(gòu)建完三角網(wǎng)之后, 就要對(duì)三角形進(jìn)行相似度比較, 以確定相互匹配的特征點(diǎn)[20]. 假設(shè)需要判斷相似性的兩個(gè)三角形分別為 ?ABC和?A′B′C′, 其中A、B、C和A′、B′、C′分別為對(duì)應(yīng)的點(diǎn)對(duì). 還假設(shè)兩個(gè)三角形之間的相似度為I, 三個(gè)對(duì)應(yīng)角度之間的相似度分別為Ia、Ib和Ic, 角A的值為a, 角A′的值為a′, 則角A和角A′的相似度公式為:

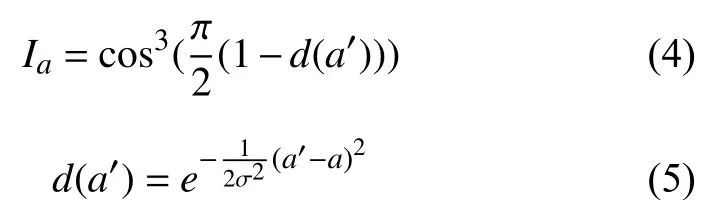
在這里, σ =a/6.

之后再分別求另兩對(duì)內(nèi)角的相似度Ib和Ic, 則?ABC和?A′B′C′為:

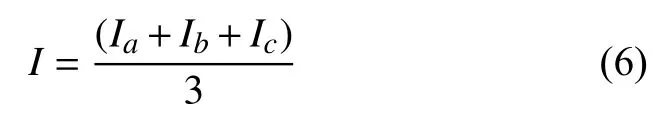
之后定義參數(shù)s, 把該參數(shù)作為判斷兩個(gè)三角形是否相似的標(biāo)準(zhǔn), 即如果計(jì)算出的兩個(gè)三角形的相似度I≥s, 則這兩個(gè)三邊形是相似三角形, 否則兩個(gè)三角形并不相似.

算法對(duì)三角網(wǎng)中的所有三角形進(jìn)行相似度計(jì)算,并構(gòu)造一個(gè)相似度矩陣D, 從中尋找相似度大于等于參數(shù)s的元素, 則該元素所對(duì)應(yīng)的三角形對(duì)就是相匹配的三角形, 以此得到精確匹配點(diǎn)對(duì).

2 高分辨率遙感圖像配準(zhǔn)改進(jìn)算法

2.1 算法思路

本文配準(zhǔn)算法的具體步驟如下:

(1) 對(duì)圖像降采樣后利用SIFT算法對(duì)圖像進(jìn)行粗配準(zhǔn). 因?yàn)閱畏叻直媛蕡D像的數(shù)據(jù)量很大, 所以從圖像上提取的特征點(diǎn)數(shù)目很多, 如果直接利用這些特征點(diǎn)進(jìn)行配準(zhǔn)的話, 會(huì)增加計(jì)算量, 影響配準(zhǔn)速度, 還容易造成誤匹配, 從而降低配準(zhǔn)精度. 因此, 在進(jìn)行配準(zhǔn)之前, 先對(duì)圖像進(jìn)行降采樣處理, 然后利用SIFT算法提取兩幅降采樣圖像的特征點(diǎn). 通過對(duì)SIFT算法進(jìn)行分析發(fā)現(xiàn), 該算法中低尺度層的特征點(diǎn)往往對(duì)應(yīng)的是高分辨率圖像中較小尺寸地物, 比如城市區(qū)域中的建筑物等, 由于尺寸較小的地物在高分辨率圖像中容易發(fā)生變化, 所以這類特征點(diǎn)的提取一般容易出現(xiàn)錯(cuò)誤;而算法中的高尺度層的特征點(diǎn)則對(duì)應(yīng)的是一些尺寸比較大的地方, 比如說大面積的草坪、廣場(chǎng)等等, 這類特征點(diǎn)一般比較穩(wěn)定, 不會(huì)輕易的就發(fā)生變化[17]. 所以本文在進(jìn)行粗配準(zhǔn)時(shí), 選用的就是這些比較穩(wěn)定的特征點(diǎn). 首先在進(jìn)行SIFT尺度空間構(gòu)建時(shí), 把第三組及其以上尺度空間的特征點(diǎn)作為該尺度空間的高尺度特征點(diǎn), 其它尺度空間的特征點(diǎn)作為該尺度空間的低尺度特征點(diǎn). 選擇高尺度空間的特征點(diǎn)進(jìn)行特征匹配工作,尋找待配準(zhǔn)圖像中與參考圖像中特征點(diǎn)的距離最近與次近的特征點(diǎn), 求得最近距離與次近距離的比值, 并將該值與給定閾值進(jìn)行比較來得到匹配點(diǎn)對(duì). 最后使用這些匹配點(diǎn)求得仿射變換模型, 對(duì)圖像進(jìn)行幾何校正,完成圖像粗配準(zhǔn).

(2) 在圖像分塊的基礎(chǔ)上提取特征點(diǎn), 并完成初始匹配. 在上一步之后, 得到了待精配準(zhǔn)圖像和基準(zhǔn)圖像,之后對(duì)這兩幅圖像進(jìn)行精配準(zhǔn)工作. 首先對(duì)兩幅圖像進(jìn)行分塊, 因?yàn)橹耙褜?duì)圖像進(jìn)行了粗配準(zhǔn), 所以此處對(duì)應(yīng)位置的子塊圖像構(gòu)成一組圖像子塊對(duì), 之后分別對(duì)各組圖像子塊對(duì)進(jìn)行特征點(diǎn)提取和匹配工作. 在這里使用的是SIFT算法對(duì)子塊圖像提取特征點(diǎn), 完成初始匹配工作, 得到初始匹配點(diǎn)對(duì).

(3) 構(gòu)建Delaunay三角網(wǎng), 利用三角形相似函數(shù)獲得精確匹配點(diǎn)對(duì). 首先使用逐點(diǎn)插入算法進(jìn)行Delaunay三角形剖分, 得到三角形網(wǎng). 之后針對(duì)三角形網(wǎng)使用三角形相似函數(shù)來度量三角網(wǎng)中所有三角形對(duì)之間的相似度, 構(gòu)建相似度矩陣, 從中選取相似度大于等于判斷標(biāo)準(zhǔn)s的三角形對(duì)作為候選三角形對(duì), 該三角形對(duì)所對(duì)應(yīng)的頂點(diǎn)對(duì)就是精確匹配點(diǎn)對(duì). 本文對(duì)這一步的改進(jìn)之處在于求解三角形對(duì)之間相似性時(shí), 不需要計(jì)算整幅圖像三角形之間的相似度, 而是利用第二步的圖像分塊, 分別在子圖像上構(gòu)建三角網(wǎng), 然后計(jì)算一組圖像子塊對(duì)之間的三角形相似度矩陣這樣可以大大減少計(jì)算量, 提高匹配效率. 最后得到了每組子圖像對(duì)之間的精確匹配點(diǎn)對(duì), 然后把這些子圖像匹配點(diǎn)對(duì)的坐標(biāo)轉(zhuǎn)化為分塊之前圖像中點(diǎn)的坐標(biāo), 以便之后進(jìn)行整幅圖像的精配準(zhǔn).

(4) 在獲得精確匹配點(diǎn)對(duì)之后, 進(jìn)行仿射模型變換,求解空間變換模型, 對(duì)圖像進(jìn)行幾何校正, 完成最終的圖像配準(zhǔn).

根據(jù)上述算法步驟, 總結(jié)算法具體流程如圖1所示.

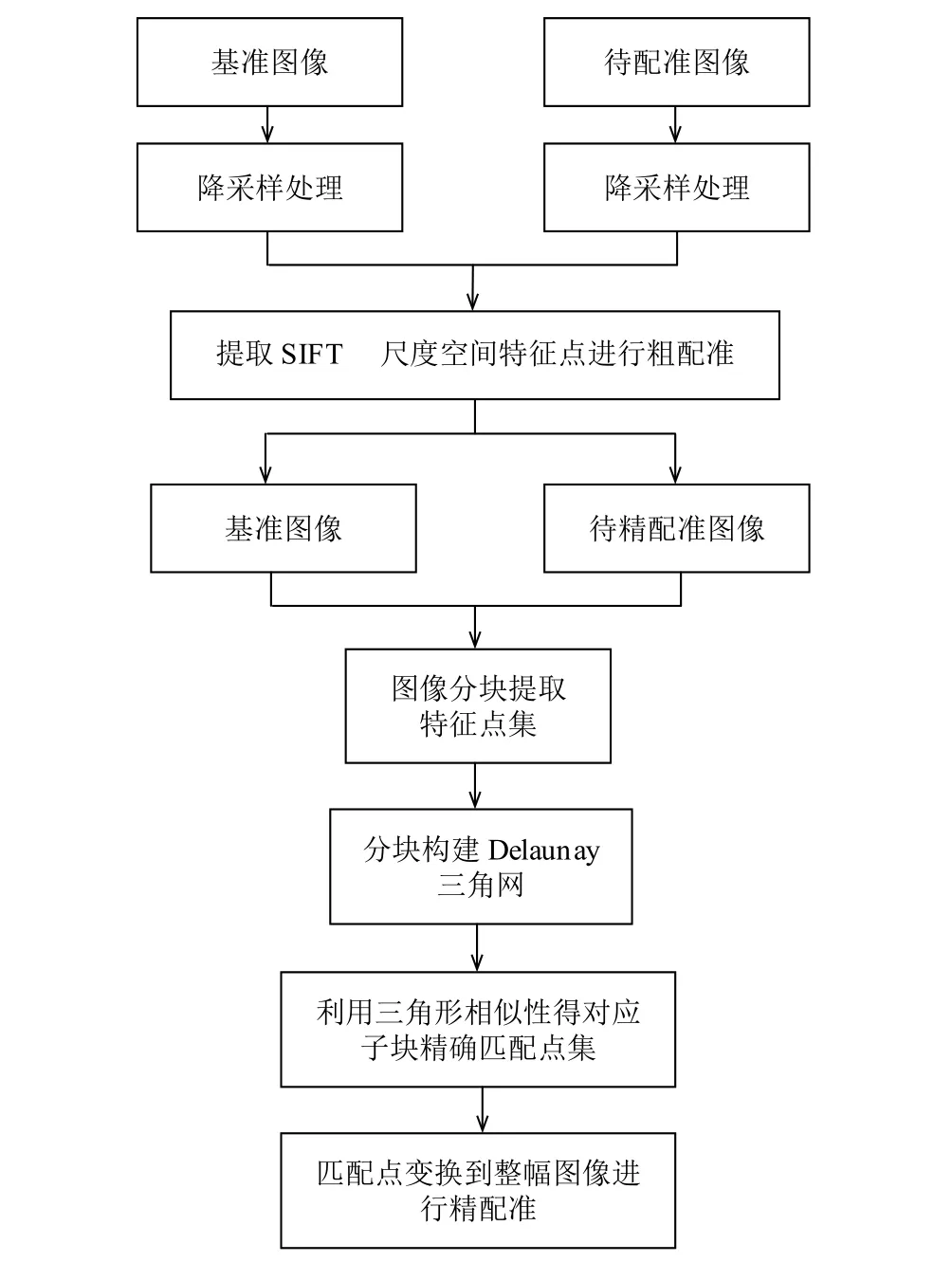
圖1 改進(jìn)算法流程圖

2.2 評(píng)價(jià)標(biāo)準(zhǔn)

本文采用CMR和RMSE作為評(píng)價(jià)指標(biāo)對(duì)配準(zhǔn)精確度進(jìn)行描述.

其中, 公式(7)中,N是參與匹配的特征點(diǎn)個(gè)數(shù),n是正確匹配點(diǎn)個(gè)數(shù), 則CMR求得的是正確匹配點(diǎn)率.CMR越大, 正確匹配點(diǎn)率越高, 那么用該匹配點(diǎn)對(duì)求得的轉(zhuǎn)換模型就越精確, 配準(zhǔn)精度也就越高. 公式(8)、(9)、(10)中,t11、t12、t21、t22、tx和ty分別是求得的仿射變換模型的參數(shù);(x1i,y1i)是基準(zhǔn)圖像的特征點(diǎn)坐標(biāo), (x2i,y2i)是與基準(zhǔn)圖像相對(duì)應(yīng)的待精配準(zhǔn)圖像特征點(diǎn)坐標(biāo), 而(x1i′,y1i′)是待精配準(zhǔn)圖像圖像的特征點(diǎn)進(jìn)行仿射變換后求得的點(diǎn)坐標(biāo). 那么RMSE公式的含義就是利用求得的轉(zhuǎn)換模型參數(shù), 計(jì)算待精配準(zhǔn)圖像坐標(biāo)經(jīng)過準(zhǔn)換后的坐標(biāo)值, 并將其與基準(zhǔn)圖像的坐標(biāo)值進(jìn)行比較, 求兩者的標(biāo)準(zhǔn)誤差來評(píng)價(jià)配準(zhǔn)的精確度. 在這里用RMSE來衡量配準(zhǔn)精度,RMSE的值越小, 配準(zhǔn)精度越高.

3 配準(zhǔn)實(shí)驗(yàn)結(jié)果及分析

3.1 實(shí)驗(yàn)數(shù)據(jù)和實(shí)驗(yàn)環(huán)境

本文的實(shí)驗(yàn)數(shù)據(jù)是由三組城市區(qū)域遙感衛(wèi)星圖像組成, 第一組是OVS-1A/B衛(wèi)星于2017拍攝的美國(guó)達(dá)拉斯市區(qū)遙感影像, 全色圖像分辨率為1.98米, 多光譜圖像分辨率也為1.98米, 圖像大小為3396× 2644. 第二組是lUtraCam-D衛(wèi)星于2005年拍攝的伊朗首都德黑蘭的兩幅RGB圖, 兩幅圖像的大小都為1256× 1278.第三組圖像也是由lUtraCam-D衛(wèi)星于2005年拍攝的伊朗首都德黑蘭的兩幅RGB圖, 兩幅圖像大小為1161× 1169. 圖2是本文實(shí)驗(yàn)數(shù)據(jù)圖.

本實(shí)驗(yàn)是在Windows 10操作系統(tǒng)的運(yùn)行環(huán)境中完成的, 計(jì)算機(jī)配置是Intel(R)Core(TM) i5-7200U 2.50 GHz CPU, 內(nèi)存8 GB, 使用Matlab 2013a軟件實(shí)現(xiàn)編程運(yùn)行.

3.2 實(shí)驗(yàn)結(jié)果及分析

3.2.1 實(shí)驗(yàn)分析過程

本文針對(duì)以下幾個(gè)問題進(jìn)行了對(duì)比實(shí)驗(yàn):

首先針對(duì)三組圖像, 分別使用SIFT算法和本文算法提取特征點(diǎn), 比較兩種方法提取特征點(diǎn)數(shù)目的不同.分析本文算法與SIFT, 得出兩種方法在計(jì)算量上的差異.

其次針對(duì)三角形相似度判斷標(biāo)準(zhǔn)s的合適取值問題, 對(duì)s不同取值下獲得的正確匹配點(diǎn)率進(jìn)行實(shí)驗(yàn)對(duì)比, 找出恰當(dāng)?shù)膮?shù)大小.

再次針對(duì)匹配階段獲得精確匹配點(diǎn)對(duì)的問題, 對(duì)Delaunay三角形剖分和傳統(tǒng)方法使用的RANSAC(隨機(jī)采樣一致性)算法進(jìn)行對(duì)比實(shí)驗(yàn), 分析兩種算法的正確匹配點(diǎn)率, 得出最佳匹配算法.

最后對(duì)本文改進(jìn)算法和傳統(tǒng)SIFT算法的配準(zhǔn)精度進(jìn)行評(píng)價(jià), 顯示最終的配準(zhǔn)效果圖.

圖2 實(shí)驗(yàn)數(shù)據(jù)圖

3.2.2 實(shí)驗(yàn)對(duì)比結(jié)果

首先是對(duì)圖像提取特征點(diǎn)的工作. 對(duì)三組圖像分別用傳統(tǒng)SIFT算法和本文算法提取特征點(diǎn), 比較兩種算法在特征點(diǎn)提取上的不同. 圖3(a)是第一組遙感圖像分別使用SIFT和本文算法提取特征點(diǎn)圖;圖3(b)是第二組圖像分別使用SIFT和本文算法提取的特征點(diǎn)圖;圖3(c)是第三組圖像分別使用SIFT和本文算法提取的特征點(diǎn)圖. 從圖中可以看出, 傳統(tǒng)SIFT算法提取的特征點(diǎn)數(shù)目過多, 三組圖像提取的特征點(diǎn)數(shù)分別是5546、1088和760個(gè)特征點(diǎn);而使用本文算法對(duì)三組圖像提取特征點(diǎn)數(shù)目分別為2559、719、521. 通過比較分析可以得出, 本文算法確實(shí)大大減少了提取的特征點(diǎn)數(shù)目, 減少了計(jì)算量, 降低了計(jì)算復(fù)雜度.

實(shí)驗(yàn)中, 本文使用的分塊大小是n1=512,n2=424, 預(yù)留邊界的大小是15%的分塊大小. 在三角形相似度計(jì)算中, 對(duì)參數(shù)s的設(shè)定進(jìn)行了試驗(yàn)分析, 分析結(jié)果如表1.

從表1中可以看出, 參數(shù)s的適合大小是0.75. 本文不同參數(shù)提取的特征點(diǎn)數(shù)目相差不大, 但是當(dāng)參數(shù)大于0.75時(shí), 正確匹配點(diǎn)率雖然會(huì)高, 但是正確匹配點(diǎn)的數(shù)目是逐漸減少的, 當(dāng)參數(shù)小于0.75時(shí), 會(huì)提取出較多的錯(cuò)誤匹配點(diǎn), 所以選擇了一個(gè)恰當(dāng)?shù)膮?shù)0.75.

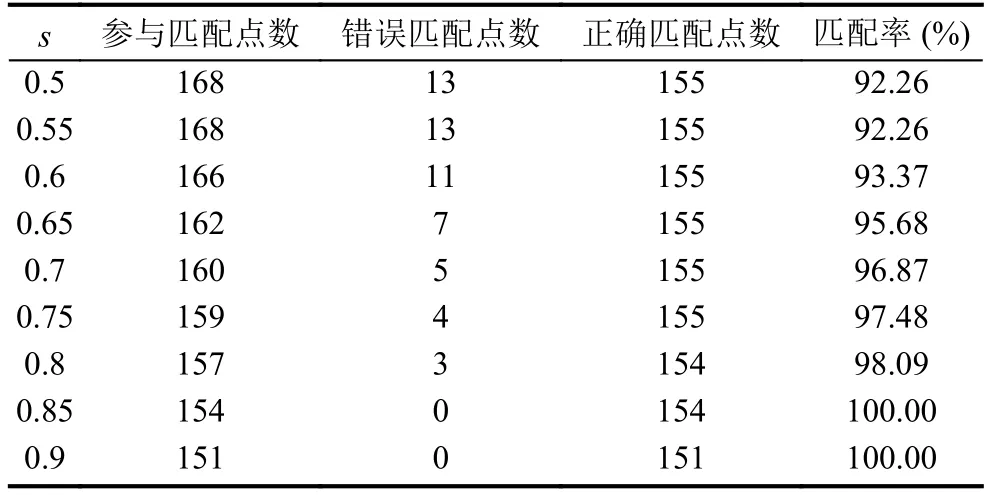
表1 使用不同參數(shù)s的匹配結(jié)果

其次在特征點(diǎn)匹配工作上, 本文利用三角形相似度度量的方法與RANSAC算法進(jìn)行了對(duì)比實(shí)驗(yàn), 結(jié)果如圖4和圖5所示, 圖4(a)是對(duì)第一組圖像使用傳統(tǒng)SIFT算法使用RANSAC算法之后得到的精確匹配點(diǎn),圖4(b)是它的連線圖. 而圖5是本文算法中, 使用RANSAC算法和Delaunay三角形剖分得到的精確匹配點(diǎn)的對(duì)比圖. 圖5(a)和(b)是第一組和第三組圖像得到的待精配準(zhǔn)圖像與基準(zhǔn)圖像, 圖5(c)和(d)是本文算法對(duì)第一組和第三組圖像分塊子圖像使用RANSAC算法后的匹配點(diǎn)圖, 圖5(e)和(f)是對(duì)第一組和第三組圖像相同的子圖像對(duì)使用Delauany三角剖分構(gòu)建了的三角網(wǎng)圖像, 圖5(g)和(h)是對(duì)第一組和第三組圖像進(jìn)行三角形相似度度量得到的精確匹配點(diǎn). 可以看出, 本文算法使用Delaunay三角剖分進(jìn)行精確匹配后,誤匹配點(diǎn)的數(shù)目減少了, 且正確匹配點(diǎn)數(shù)目比RANSAC算法得到的正確匹配點(diǎn)數(shù)目多. 表2、表3分別是第一和第三組圖像在提取精確匹配點(diǎn)時(shí), 使用RANSAC算法和Delaunay三角形剖分得到的精確匹配點(diǎn)結(jié)果對(duì)比.

圖4 使用傳統(tǒng)SIFT算法得到的匹配點(diǎn)及其連線圖

圖5 使用RANSAC和Delaunay三角剖分分別進(jìn)行匹配點(diǎn)配對(duì)的效果圖

表2 第一組圖像使用RANSAC和Delaunay方法提取正確匹配點(diǎn)對(duì)比

表3 第三組圖像使用RANSAC和Delaunay方法提取正確匹配點(diǎn)對(duì)比

從表中可以看出, 使用Delaunay三角形剖分提取的精確匹配點(diǎn)數(shù)目多且減少了誤匹配點(diǎn)的數(shù)目.

最后計(jì)算SIFT算法和本文算法的RMSE和CMR,可以得到, 第一組圖像使用SIFT算法的正確匹配點(diǎn)率為91.33%, 本文算法的正確匹配點(diǎn)率為97.48%;第三組圖像使用SIFT算法的正確匹配點(diǎn)率為81.25%, 本文算法的正確匹配點(diǎn)率為93.18%, 說明本文算法的正確匹配點(diǎn)率高于傳統(tǒng)SIFT算法. 而第一組圖像使用本文算法的RMSE為1.76, 傳統(tǒng)SIFT算法得到的RMSE為3.15;第三組圖像使用本文算法的RMSE為1.28, 傳統(tǒng)SIFT算法得到的RMSE為2.56, 說明本文算法的配準(zhǔn)精度高于傳統(tǒng)SIFT算法. 表4、表5分別為第一組和第三組圖像使用SIFT算法和本文算法的RMSE、CMR以及運(yùn)行時(shí)間的對(duì)比. 從表中可以看出,本文算法運(yùn)行時(shí)間比SIFT較小. 圖6是本文最終配準(zhǔn)結(jié)果圖.

表4 第一組圖像本文方法與SIFT方法的精度評(píng)價(jià)

表5 第三組圖像本文方法與SIFT方法的精度評(píng)價(jià)

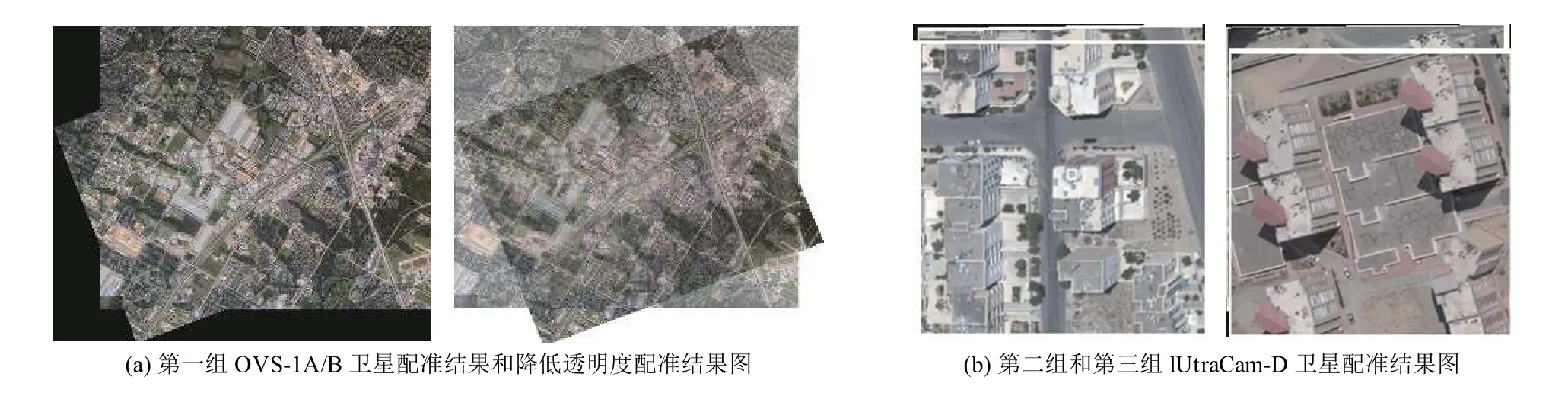
圖6 配準(zhǔn)結(jié)果圖

4 結(jié)論與展望

針對(duì)高分辨率遙感圖像配準(zhǔn)中圖像本身數(shù)據(jù)量過大且存在誤匹配點(diǎn)的問題, 本文提出了一種基于SIFT和Delaunay三角網(wǎng)的高分辨率遙感圖像配準(zhǔn)方法, 該方法分為粗配準(zhǔn)和精配準(zhǔn)兩個(gè)階段. 為了降低高分辨率遙感圖像本身的數(shù)據(jù)量, 在進(jìn)行配準(zhǔn)工作之前采用降采樣方法處理兩幅圖像. 之后僅提取高尺度空間下的SIFT特征點(diǎn)用于粗配準(zhǔn). 之后進(jìn)入精配準(zhǔn)階段,為了提取均勻分布的特征點(diǎn), 本文引入了圖像分塊策略, 對(duì)待精配準(zhǔn)圖像進(jìn)行圖像分塊. 之后對(duì)每幅子塊圖像提取特征點(diǎn)并構(gòu)建Delaunay三角網(wǎng), 利用三角形相似函數(shù)求得精確匹配點(diǎn)對(duì), 然后將得到的子匹配點(diǎn)對(duì)坐標(biāo)轉(zhuǎn)化為分塊之前圖像中點(diǎn)的坐標(biāo), 以便進(jìn)行整幅圖像的精配準(zhǔn)工作. 從實(shí)驗(yàn)中可以看出, 該算法提取的特征點(diǎn)是減少的, 且算法的正確匹配點(diǎn)率要大于傳統(tǒng)SIFT算法得到的正確匹配點(diǎn)率, 因此, 本文算法配準(zhǔn)精度更高. 但是受實(shí)驗(yàn)數(shù)據(jù)的限制, 本文只是針對(duì)城市建筑物區(qū)域遙感衛(wèi)星像進(jìn)行實(shí)驗(yàn), 并未對(duì)非城市建筑物圖像或其他類別圖像進(jìn)行實(shí)驗(yàn), 且算法速率也有待于進(jìn)一步優(yōu)化.