復(fù)雜邊界下大渦模擬的格子Boltzmann并行方法

徐 磊 宋安平 劉智翔 張 武

1(上海大學(xué)計(jì)算機(jī)工程與計(jì)算科學(xué)學(xué)院 上海 200444)2(上海海洋大學(xué)信息學(xué)院 上海 201306)

0 引 言

格子Boltzmann方法LBM是介于流體的微觀分子動(dòng)力學(xué)模型和宏觀連續(xù)模型之間的介觀模型。由于Boltzmann方程自身的運(yùn)動(dòng)學(xué)特性，以及可以根據(jù)經(jīng)典的Chapman-Enskog展開(kāi)從LBM得到Navier-Stokes方程，使得LBM比基于連續(xù)介質(zhì)假設(shè)的Navier-Stokes方程包含了更多的物理內(nèi)涵。目前，LBM已經(jīng)應(yīng)用在了很多流體問(wèn)題(多項(xiàng)流、湍流、多孔介質(zhì)以及微尺度流等)中[1-4]。LBM將流體視為比分子大，但在宏觀上無(wú)限小的一系列粒子。這些粒子按照一定物理規(guī)律在網(wǎng)格上進(jìn)行演化計(jì)算，通過(guò)對(duì)反映粒子狀態(tài)的分布函數(shù)進(jìn)行統(tǒng)計(jì)平均求得宏觀物理量。

文獻(xiàn)[5-6]首先分別提出了單松弛時(shí)間格子Boltzmann模型SRT-LBM(Single-Relaxation-Time LBM)和格子BGK模型LBGK(Lattice Bhatnagar-Gross-Krook)。它們采用單一松弛時(shí)間系數(shù)，計(jì)算效率得到極大提高。盡管SRT-LBM已經(jīng)被成功地應(yīng)用于模擬各種流體問(wèn)題，但是該模型仍然存在缺點(diǎn)：當(dāng)無(wú)量綱松弛時(shí)間過(guò)于趨近0.5時(shí)，模型會(huì)產(chǎn)生數(shù)值不穩(wěn)定導(dǎo)致程序發(fā)散。針對(duì)這一問(wèn)題，D′Humiéres[7]提出了廣義格子Boltzmann模型GLBE(Generalized Lattice Boltzmann Equation)，或稱為多松弛格子Boltzmann模型MRT-LBM(Multiple-Relaxation-Time LBM)。2000年-2002年間，文獻(xiàn)[8-10]對(duì)該模型對(duì)該模型二維和三維的物理原理、參數(shù)選取、數(shù)值穩(wěn)定性和計(jì)算效率等方面進(jìn)行了詳細(xì)的理論分析，表明了MRT-LBM的穩(wěn)定性和精確性都要優(yōu)于SRT-LBM。

相對(duì)于SRT-LBM，MRT-LBM穩(wěn)定性更高，但是并未克服松馳時(shí)間趨近于0.5時(shí)計(jì)算不穩(wěn)定導(dǎo)致程序發(fā)散的問(wèn)題。隨著雷諾數(shù)的增大，MRT-LBM和SRT-LBM雖然都可通過(guò)增加網(wǎng)格數(shù)保持計(jì)算穩(wěn)定，但是當(dāng)雷諾數(shù)更大時(shí)，利用SRT-LBM和MRT-LBM直接數(shù)值模擬流場(chǎng)全部動(dòng)態(tài)信息所需要的內(nèi)存和求解時(shí)間非常巨大[11]。為了在模擬湍流場(chǎng)時(shí)節(jié)省計(jì)算耗費(fèi)并在有限的計(jì)算機(jī)硬件條件下盡可能完整地給出瞬時(shí)流場(chǎng)信息，可在格子Boltzmann模型中引入大渦模擬技術(shù)LES(Large Eddy Simulation)[12]。Hou等[13-14]通過(guò)非平衡粒子分布函數(shù)的二階矩計(jì)算了應(yīng)變率張量，從而將Smagorinsky渦粘性模型引入SRT-LBM中。而Kxafczyk等[15]則利用傳遞矩陣將粒子分布函數(shù)的二階矩從速度空間傳遞到矩空間計(jì)算禍粘性系數(shù)，將Smagorinsky渦粘性模型與D3Q15 MRT-LBM組合。文獻(xiàn)[16-17]通過(guò)Chapman-Enskog分析推導(dǎo)應(yīng)變率張量，分別將Smagroinsky模型引入到D3Q19 MRT-LBM和包含外力項(xiàng)的D3Q19 MRT-LBM中，得到MRT-LBM-LES(MRT-LBM with LES)模型。

如今，計(jì)算流體力學(xué)研究對(duì)象的規(guī)模和復(fù)雜程度向更大更深的方向發(fā)展，單個(gè)計(jì)算節(jié)點(diǎn)不能滿足計(jì)算需求，需要借助于高性能計(jì)算機(jī)滿足計(jì)算的需要。大規(guī)模并行計(jì)算在一定程度上可以解決計(jì)算需要和超級(jí)計(jì)算性能之間的矛盾。LBM中格點(diǎn)演化主要分為碰撞和遷移兩個(gè)過(guò)程，碰撞是各個(gè)格點(diǎn)獨(dú)自同時(shí)進(jìn)行的，只與格點(diǎn)自身相關(guān)。遷移時(shí)格點(diǎn)上的粒子也只是與離它們最近格點(diǎn)上的粒子進(jìn)行信息交換，所以LBM非常適合并行計(jì)算。諸多研究人員對(duì)LBM的并行性能進(jìn)行了研究，設(shè)計(jì)了高可擴(kuò)展高效率的并行算法。Pan等[19]在不同并行計(jì)算平臺(tái)比較區(qū)域劃分方法的性能，利用D3Q15模型模擬了單向和多項(xiàng)流在多孔介質(zhì)中的流動(dòng)情況。Wu等[20]對(duì)高雷諾數(shù)二維方腔流，采用域分解方法對(duì)D2Q9 MRT-LBM和SRT-LBM進(jìn)行了比較。Velivelli等[21]利用CPU緩存的優(yōu)勢(shì)，將計(jì)算區(qū)域分塊循環(huán)計(jì)算，加快了計(jì)算速度。Schepke等[22]采用塊劃分策略對(duì)SRT-LBM進(jìn)行了并行性能的分析，該方法使得每個(gè)進(jìn)程都分配到整個(gè)計(jì)算區(qū)域中的一個(gè)子計(jì)算區(qū)域，各個(gè)子計(jì)算區(qū)域與相鄰的子計(jì)算區(qū)域進(jìn)行數(shù)據(jù)的傳遞。文獻(xiàn)[23]針對(duì)多孔介質(zhì)內(nèi)流體流動(dòng)提出了負(fù)載均衡策略減少計(jì)算時(shí)間。本文主要研究了MRT-LBM引入Smagorinsky渦粘性模型后在大規(guī)模并行計(jì)算機(jī)上的并行性能。

1 MRT-LBM-LES以及邊界條件

1.1 MRT-LBM-LES

MRT-LBM將速度空間的碰撞通過(guò)線性變換轉(zhuǎn)化為矩空間的碰撞，使得作用后得到的量具有物理意義。在矩空間完成碰撞后，再進(jìn)行逆變換到速度空間，進(jìn)行遷移的過(guò)程。MRT-LBM的碰撞過(guò)程是在矩空間中進(jìn)行的，它的演化方程為：

f(x+ciδt,t+δt)-f(x,t)=-M-1S[m(x,t)-meq(x,t)]

(1)

式中：f(x,t)是粒子分布函數(shù)，M是變換矩陣，m(x,t)=Mf(x,t)是矩空間的粒子分布函數(shù)，meq(x,t)是矩空間的平衡態(tài)分布函數(shù)。S是松弛對(duì)角陣，并且S對(duì)角線各項(xiàng)滿足0≤Si<2。

式(1)可以分為碰撞和遷移兩個(gè)過(guò)程:

f(x,t)=f(x,t)-M-1S[m(x,t)-meq(x,t)]

(2)

f(x+ciδt,t+δt)=f(x,t)

(3)

常用的二維LBM模型為D2Q9(如圖1所示)。它的離散速度為:

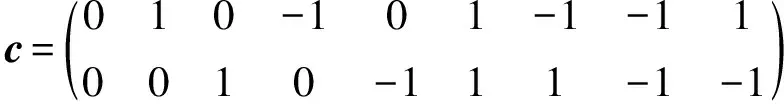
(4)

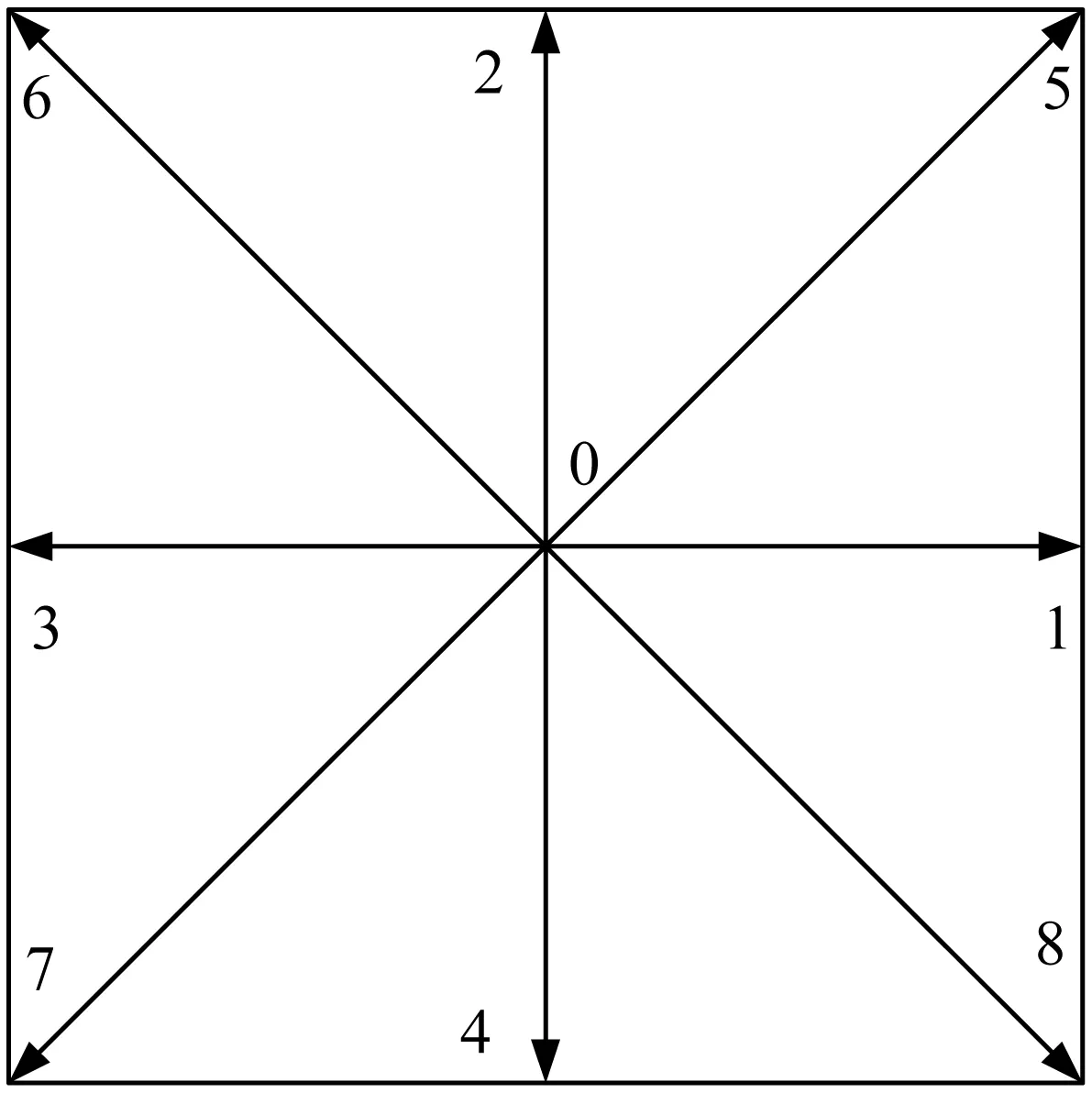
圖1 D2Q9

平衡態(tài)分布函數(shù):

(5)

(6)

D2Q9對(duì)應(yīng)的變換矩陣:

(7)

矩空間的平衡態(tài)分布函數(shù)meq為:

meq=ρ(1,-2+3u2,α+βu2,ux,-ux,uy,-uy,

(8)

式中:α和β為自由參數(shù)，ρ為密度，u為速度。松弛矩陣diag(0,se,sε,0,sq,0,sq,sv,sv)。剪切粘性和體粘性系數(shù)分別為：

(9)

(10)

宏觀量為:

ρ=∑fi

(11)

(12)

為了能夠模擬湍流，Hou等[13]將Smagroinsky模型引入到D2Q9中。在引入的Smagorinsky模型中，無(wú)量綱的運(yùn)動(dòng)粘性系數(shù)v由分子運(yùn)動(dòng)粘性v0和渦粘性vt組成:

υ=v0+vt

(13)

式中：vt由應(yīng)變率張量Sαβ，參數(shù)Cs以及格子步長(zhǎng)δx決定,其表達(dá)式如下：

vt=(Csδx)2|Sαβ|

(14)

1.2 邊界條件

在處理曲面復(fù)雜邊界時(shí)，如果使用平直邊界的邊界處理方法，精度較低。為此，Yu等[24]提出了一種曲面邊界的處理方法。如圖2所示，實(shí)心圓表示固體點(diǎn)，空心圓表示流場(chǎng)點(diǎn)，曲線表示實(shí)際的物理邊界，它將流場(chǎng)分為固體點(diǎn)和流場(chǎng)點(diǎn)，方格點(diǎn)為邊界節(jié)點(diǎn)。

圖2 曲面邊界

這里將流場(chǎng)點(diǎn)記為xf，固體點(diǎn)記為xb，與xf相鄰的流場(chǎng)點(diǎn)記為xff，邊界點(diǎn)記為xw。則流場(chǎng)點(diǎn)xf的分布函數(shù)為：

(15)

(16)

對(duì)于平直邊界，本文采用Guo等[25]提出的非平衡態(tài)外推方法。

2 格子類(lèi)型的判斷

當(dāng)流場(chǎng)中物體存在復(fù)雜邊界時(shí)，需要判斷物體附近格子點(diǎn)的類(lèi)型，通過(guò)不同類(lèi)型的格子點(diǎn)計(jì)算出物體邊界處的格子點(diǎn)粒子分布函數(shù)。本文通過(guò)射線法判斷格子的類(lèi)型。從待判斷點(diǎn)的某一個(gè)方向引射線，計(jì)算和物體邊界的交點(diǎn)個(gè)數(shù)，通過(guò)交點(diǎn)個(gè)數(shù)的奇偶性得到格子點(diǎn)的類(lèi)型。本文使用圓柱和Rae2822翼型為例判斷格子點(diǎn)的類(lèi)型，如圖3和圖4所示。該方法可以準(zhǔn)確的判斷出圓柱和翼型流場(chǎng)中的格子類(lèi)型。

圖3 圓的格子類(lèi)型(包括固體點(diǎn)和邊界點(diǎn))

圖4 Rae2822翼型的格子類(lèi)型(包括固體點(diǎn)和邊界點(diǎn))

3 并行策略

對(duì)于二維問(wèn)題，流場(chǎng)可以沿著一個(gè)方向或兩個(gè)方向進(jìn)行劃分。當(dāng)并行環(huán)境中核數(shù)增多時(shí)，沿著一個(gè)方向進(jìn)行劃分并不符合實(shí)際問(wèn)題的需要，所以本文選擇沿著兩個(gè)方向?qū)α鲌?chǎng)進(jìn)行劃分。在進(jìn)行并行處理時(shí)，每個(gè)MPI進(jìn)程負(fù)責(zé)處理一個(gè)流場(chǎng)的子區(qū)域，每個(gè)子區(qū)域用一個(gè)二元組(i,j)標(biāo)記。進(jìn)程總數(shù)記為n。二元組可以通過(guò)下式獲得：

i=mod(n,nx)

(17)

(18)

式中：nx為沿著x方向的劃分?jǐn)?shù)。每個(gè)子區(qū)域的范圍為:

(19)

(20)

式中：nLx是x方向格子點(diǎn)數(shù)，xmin是子區(qū)域的起始格點(diǎn)位置，xmax是子區(qū)域的結(jié)束格點(diǎn)位置。子區(qū)域在y方向的范圍可以類(lèi)似計(jì)算得到。

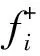
圖5 進(jìn)程(i,j)傳遞部分?jǐn)?shù)據(jù)給進(jìn)程(i+1,j)

圖6 流場(chǎng)中各個(gè)子區(qū)域信息傳遞

4 數(shù)值實(shí)驗(yàn)

4.1 數(shù)值驗(yàn)證

為了驗(yàn)證本文并行算法的正確性，我們使用圓柱和翼型在流場(chǎng)中的情況分別進(jìn)行了測(cè)試。流場(chǎng)的速度為U=0.115 5。圖7中，(a)和(b)是圓柱繞流雷諾數(shù)Re=20和40時(shí)的流線圖，從圖中可以看出，在圓柱后產(chǎn)生了一對(duì)對(duì)稱的渦，隨著雷諾數(shù)的增大，渦也在逐漸變大。(c)和(d)是雷諾數(shù)Re=100和150時(shí)的流線圖，圓柱后方兩側(cè)的渦隨著雷諾數(shù)的增大開(kāi)始出現(xiàn)震蕩，當(dāng)超過(guò)臨界值時(shí)，圓柱后的渦逐漸分離，形成周期性交替脫落、旋轉(zhuǎn)方向相反的非對(duì)稱渦[26]。

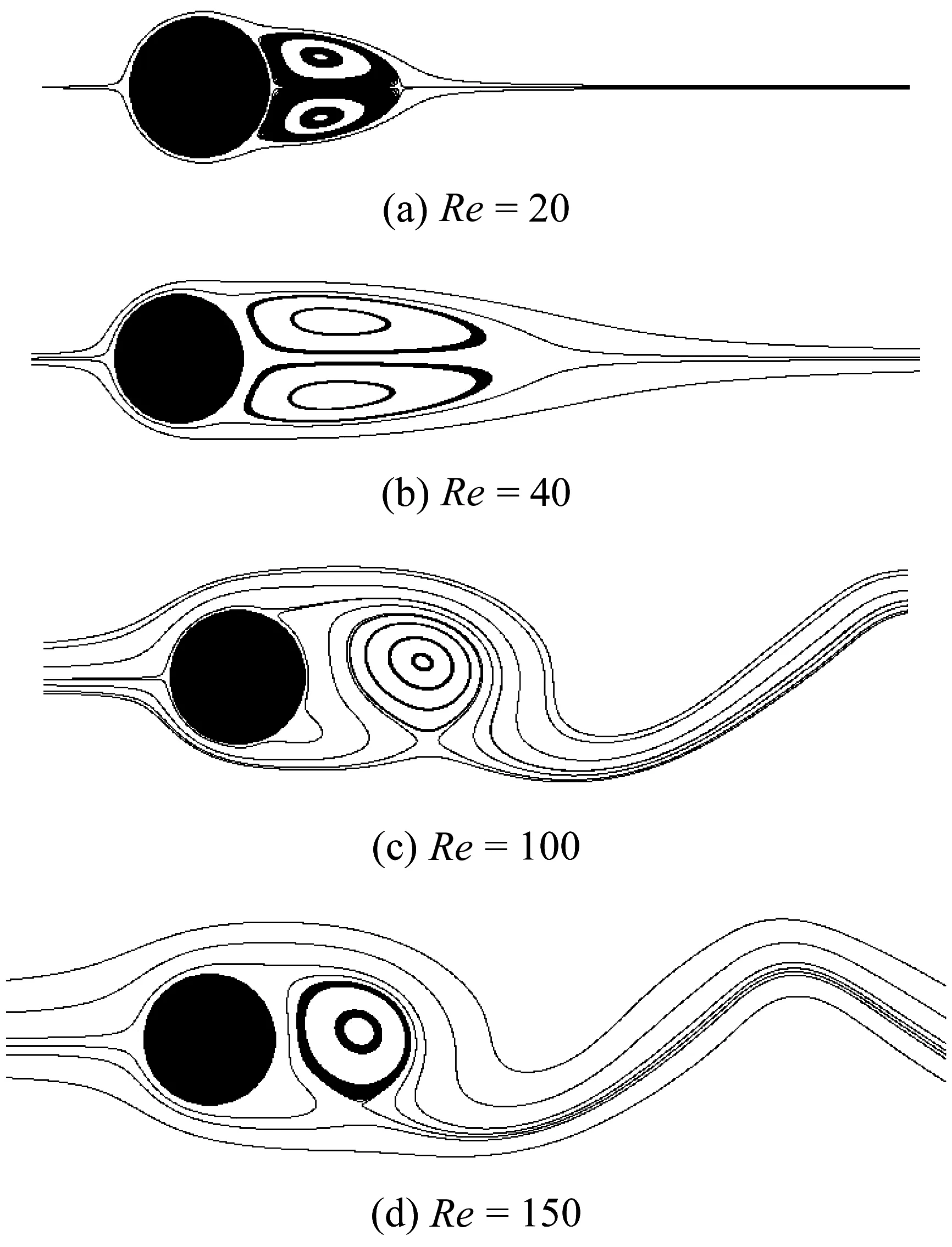
圖7 圓柱繞流流線圖

圖8中的(a)和(b)是翼型繞流雷諾數(shù)Re=100 000時(shí)的流線圖，(a)的攻角為0°，(b)的攻角為3°。可以看出，實(shí)驗(yàn)結(jié)果與文獻(xiàn)[27]一致。

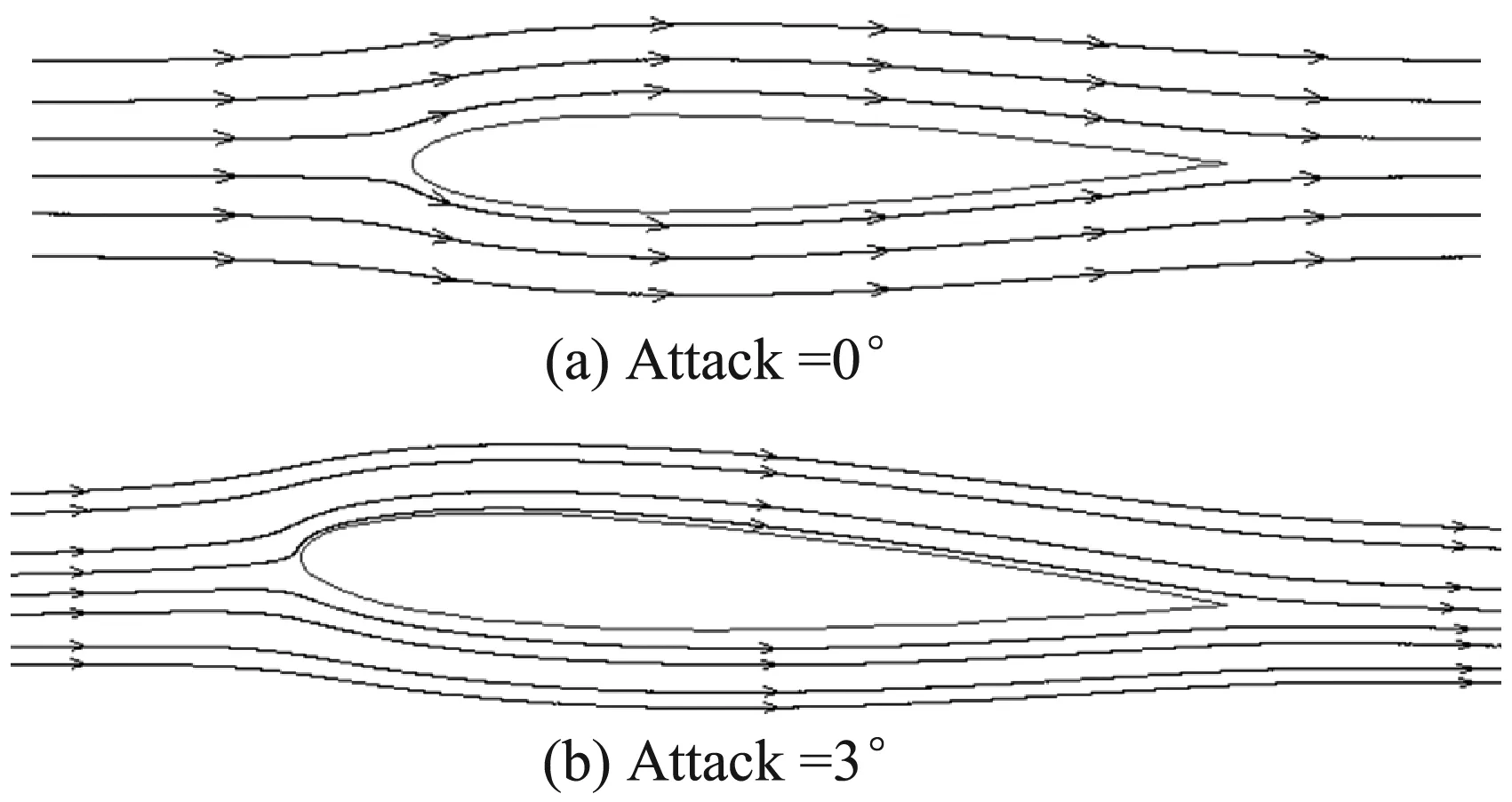
圖8 翼型繞流渦量圖

4.2 效率驗(yàn)證

本節(jié)基于128核集群進(jìn)行并行性能的測(cè)試，該集群包含1個(gè)登錄節(jié)點(diǎn)、8個(gè)計(jì)算節(jié)點(diǎn)，每個(gè)節(jié)點(diǎn)有16個(gè)核，配置了兩塊2×Intel Xeon E5-2660 CPU。每個(gè)節(jié)點(diǎn)的內(nèi)存為128 GB。節(jié)點(diǎn)之間通過(guò)56 GB Infiniband線連接。

為了統(tǒng)計(jì)程序運(yùn)行時(shí)間，進(jìn)行了500步迭代。采用了1 000×1 000和1 500×1 500兩種格子規(guī)模進(jìn)行了加速比和效率的測(cè)試，比較了兩種不同規(guī)模下的加速比和效率。

分別在核數(shù)為8、16、32、64以及128核上進(jìn)行了時(shí)間的統(tǒng)計(jì)。圖9為兩種不同格子規(guī)模下加速比的比較，圓形為格子規(guī)模1 500×1 500的加速比，正方形為格子規(guī)模1 000×1 000的加速比，黑色直線為理想加速比。可以看出，兩種格子規(guī)模的加速比都呈直線上升，格子規(guī)模較大的加速比要略高。由于進(jìn)程之間需要進(jìn)行邊界上格子信息的通信，加速比要低于理想加速比。因?yàn)檫M(jìn)程間的通信量只發(fā)生在相鄰進(jìn)程間，并沒(méi)有大規(guī)模的主從式通信，所以加速比基本為直線。

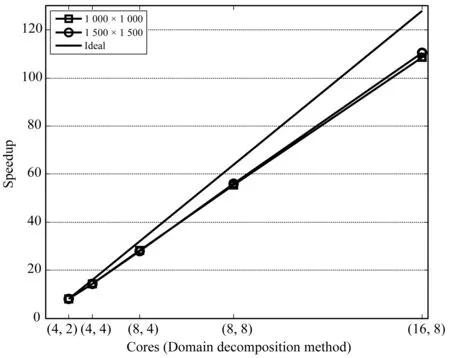
圖9 加速比

圖10為兩種不同規(guī)模下效率的比較，圓形為格子規(guī)模1 500×1 500的效率，正方形為格子規(guī)模1 000×1 000的效率。可以看出，兩種格子規(guī)模的效率都在緩慢下降，隨著核數(shù)的增加，格子規(guī)模較大的效率下降趨勢(shì)更為緩慢，當(dāng)核數(shù)達(dá)到128核時(shí)，計(jì)算效率可以達(dá)到86.5%。從圖9和圖10可以看出，我們所實(shí)現(xiàn)的并行算法有良好的可擴(kuò)展性。

圖10 效率

5 結(jié) 語(yǔ)

本文提出了一種高可擴(kuò)展的格子Boltzmann方法。該方法可以有效判斷格子類(lèi)型，模擬高雷諾數(shù)下流場(chǎng)中的湍流，采用雙向的區(qū)域分解方法，并設(shè)計(jì)了詳細(xì)的劃分策略以及數(shù)據(jù)交換策略，大大降低了通信量，減少了通信時(shí)間。數(shù)值結(jié)果表明，該算法具有良好的可擴(kuò)展性，效率可以在128個(gè)核心上達(dá)到86.5%。