三階擴展GNL電池模型的研究

杜森，謝立潔，徐梓薦，翟世歡

（天津易鼎豐動力科技有限公司天津300385）

電池系統(tǒng)是新能源車輛的心臟，是車輛的動力來源，如何能夠準(zhǔn)確可靠的輸出動力是電池管理系統(tǒng)的關(guān)鍵所在。市場上對于電池管理系統(tǒng)的算法五花八門，各廠家也都各顯神通，但是歸根結(jié)底都是對電池狀態(tài)特性的估算，所以如果能夠準(zhǔn)確的估算出電池的屬性和狀態(tài)，就會減小對算法的依賴，降低產(chǎn)品的復(fù)雜程度提高電池管理系統(tǒng)的可靠性。

對電池的特性分析和估計可以從電池的化學(xué)特性開始，分析電池的原材料特性，總結(jié)和預(yù)計各化學(xué)分子的運動規(guī)律，模擬電池內(nèi)部各相關(guān)原材料的分子擴散效應(yīng)等現(xiàn)象，體現(xiàn)電池的動態(tài)變化特性。另外一種方式可以模擬電化學(xué)場域，基于電化學(xué)中電流場的相關(guān)理論進行模型的設(shè)計。上述兩種模型建立過程原理比較復(fù)雜，需要精通電化學(xué)，電磁場，物理學(xué)等比較復(fù)雜的知識，不利于推廣和應(yīng)用，而且各個電芯的化學(xué)成分也不相同，每次都需要搭建模型，工作量比較大，成本比較高。此外由于電池廠家對自己電芯配方的保密，對于電池管理系統(tǒng)開發(fā)人員基于此方法構(gòu)建模型困難比較大。

再有就是通過大數(shù)據(jù)分析，通過大量的試驗統(tǒng)計，將大數(shù)據(jù)進行整理統(tǒng)計建立模型，此方法雖然原理簡單，但是需要大量的試驗和計算，開發(fā)成本比較高，且一旦電芯成分改變或者電池管理系統(tǒng)更換單體，所有的試驗還需重新開始，數(shù)據(jù)需要重新統(tǒng)計，不適合如今快節(jié)奏的開發(fā)需求。

1 市場主流電池模型分析

基于上述建模思路的弊端，現(xiàn)在市場上應(yīng)用比較多的是基于歐姆定律等物理理論創(chuàng)建等效電路模型，來模擬電池復(fù)雜的化學(xué)變化。

目前市場上最常用的是，采用如圖1中的Rint模型。

圖1 Rint模型

利用電阻R0兩端的電壓變化模擬電池充放電過程中電壓的上升和下降。此方法雖然簡單有效，但是對于估算精度要求越來越高的市場需求就有些捉襟見肘了。

圖2 Thevenin模型

在Rint模型中只是能夠簡單表征電池的電壓線性變化的特性曲線，對于電池的非線性特征就不能準(zhǔn)確表達(dá)了。所以在一些高端的BMS中提出了較為先進的Thevenin模型如圖2所示，此模型利用電容模擬電池在充放電過程中的電池非線性的特征，對BMS的各種算法能夠提供很好的數(shù)據(jù)支撐。但是對于一些化學(xué)特性比較活躍的鋰離子電池，單純的一階模擬非線性只能表征電池的特征曲線，如圖3所示。

圖3方框中是基于模型仿真的數(shù)據(jù)，從圖上可以看出精度上還是有些差距的。因此是不能滿足高精度算法需要的，特別是隨著科學(xué)技術(shù)的不斷進步，車輛的電池系統(tǒng)會越來越復(fù)雜，而對電池的安全和壽命要求也越來越高，目前市場上的這些模型對于高精度的電池管理系統(tǒng)還有些差距。針對于此筆者提出了能夠更好模擬電池特性曲線的三階擴展GNL模型。

圖3 Thevenin電池模型特征曲線

2 三階擴展 GNL等效電路模型

三階擴展GNL模型指的是利用三階RC電路對電池的特性曲線進行更加細(xì)致的分段估計，能夠使創(chuàng)建的電池模型的特性曲線更加貼合實際曲線，進而在BMS的算法中減少由于電池模型參數(shù)造成的誤差，提高結(jié)果的精確度。

2.1 模型的創(chuàng)建

三階擴展GNL模型是在Thevenin基礎(chǔ)上增加到三階RC等效電路。在圖3中可以看出Thevenin模型雖然加入了電容Cp和Rp可以表征電芯在充放電過程時的容性負(fù)載變化，但是誤差還是比較大的，因此可以增加容性負(fù)載的階數(shù)細(xì)化此部分的變化特征如圖4所示。

圖4 三階擴展GNL電池模型

Uoc模擬電池的開路電壓，可以理解為一個電壓源，電容Cb表征電池的容性負(fù)載特征，模擬放電或充電引起的電池開路電壓的變化，Cb兩端的電壓定義為Ub；R0表征電池的直流內(nèi)阻，模擬電池的線性特征；Re，Ce和Rp，Cp分別表征電池在充放電過程中的極化反應(yīng)的過程一階極化特性和二階極化特性；Rc表示了極化補償內(nèi)阻，Cc表示極化補償電容；Rs為自放電電阻。

2.2 模型參數(shù)確定需要的試驗依據(jù)

模型中的參數(shù)獲取主要是通過對單體電池HPPC（Hybrid Pulse Power Characterization）試驗獲得。通過HPPC測試獲得電池的動態(tài)特性。

為了得到較為準(zhǔn)確的模型，需要HPPC測試過程是在不同溫度、不同電流下進行測試。每次的測試過程需要恒定放電流為1C，SOC每隔10%做一個循環(huán)，電量變化10%間隔的實驗之間電池靜置1小時（。在每個復(fù)合脈沖試驗開始前測量電池電壓，以便得到對應(yīng)SOC的電池開路電壓近似值。

文中以某款三元材料的鋰電池作為研究對象，該電池容量為26 Ah，額定電壓為3.7 V。以3C放電為例得到的數(shù)據(jù)如圖5中所示。

圖5 HPPC測試曲線

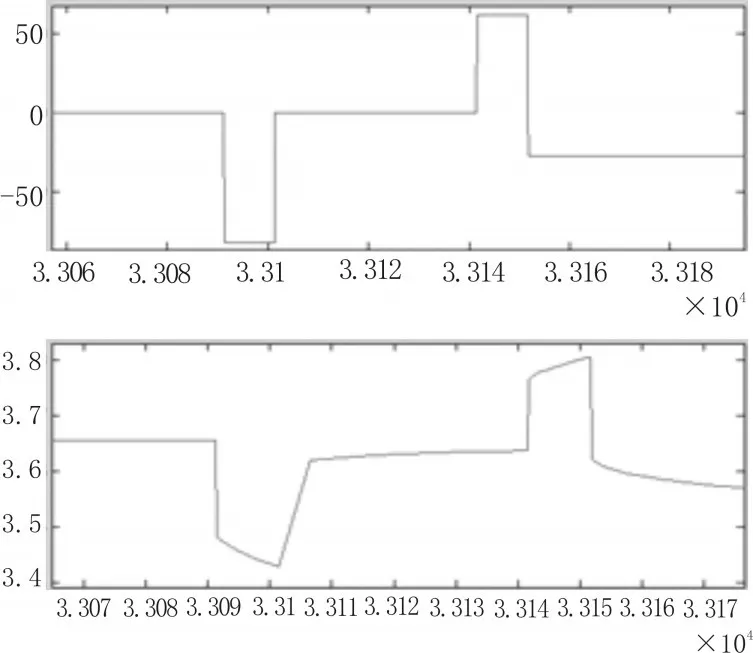
圖6 SOC為50%時HPPC測試曲線

圖5為HPPC電流示意圖和電流對應(yīng)的電壓響應(yīng)曲線，上面曲線是電流和時間的曲線，下面的曲線是對應(yīng)的電壓和時間的曲線，其中圖5和圖6分別表示了整個HPPC的過程和50%SOC時的局部細(xì)節(jié)展示。

2.3 模型中的參數(shù)確定

上述模型中的比較容易得到的是歐姆內(nèi)阻，它的特性由電池兩端電壓UL的突變表征。因此可以通過圖5中電壓的變化和電流值根據(jù)歐姆定律到歐姆內(nèi)阻，如下式所示：

模型中的其他參數(shù)的確定可以借助于Matlab/Simulink中的parameter estimation工具進行計算。首先依據(jù)一些基本的物理定律創(chuàng)建狀態(tài)方程，然后根據(jù)方程創(chuàng)建simulink模型，將試驗數(shù)據(jù)帶入模型，利用曲線擬合得到方程中的各個參數(shù)。具體原理如下闡述。

根據(jù)電容和電壓的關(guān)系方程:

以3.1提出的模型中電容兩端的電壓為狀態(tài)，基于基爾霍夫定律建立狀態(tài)方程如下

電池的輸出端電壓和模型中每一階RC電路及內(nèi)阻的電壓關(guān)系如下：

假設(shè)電池輸出端功率為PL，由能量守恒定律得出功率計算公式

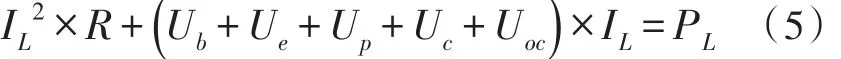
從而得出

基于式（2）對電流的積分得到Cb的電壓得到

將上式離散化得到i時刻的電池端電壓的期望值。

由3.1中的模型根據(jù)基爾霍夫電流定律可以得到三階RC電路中各個電容上的電流值如下所示

其中的τe，τp，τc為時間常數(shù)，他們的值如下所示：

基于上述原理利用MATLAB/Simulink搭建電池模型，基于最小二乘法擬合后得到模型中的各個參數(shù)值。

在Simulink模型中，以2.2章節(jié)中測試得到的電流信號作為模型的輸入信號，電壓信號作為輸出信號帶入上述的狀態(tài)方程，利用Simulink中的parameter estimation工具自動進行估算得出模型中的各個參數(shù)值。

2.4 電池模型的驗證

為了驗證電池模型的精確性，可以將計算結(jié)果帶回到2.1中的模型進行輸出結(jié)果的比較。

圖7 三階擴展GNL電池模型特性曲線

圖7中淺色的曲線表示的原始的試驗數(shù)據(jù)輸出，即測量到的真實的電壓曲線。深色的是基于創(chuàng)建的電池模型，計算得到的輸出曲線。通過數(shù)據(jù)比較可以看出創(chuàng)建的電池模型基本跟實際的電池相吻合。比市場上現(xiàn)在較先進的Thevenin模型（圖3）在精度上有了很大的提升，為高精度的BMS算法提供了很好的支撐。

3 結(jié)論

在BMS的開發(fā)過程中無論采用何種算法都是基于創(chuàng)建電池模型的基礎(chǔ)上進行的，如果創(chuàng)建的電池模型跟實際的電池出入較大，無論算法有多先進都不可能得到準(zhǔn)確的結(jié)果。電池模型中各個參數(shù)的精確性決定了BMS中所有算法的結(jié)果，是BMS開發(fā)中最重要也是最基礎(chǔ)的內(nèi)容，它的準(zhǔn)確與否直接決定著最終的結(jié)果。本文介紹的電池模型的創(chuàng)建方法簡單有效，且精確度很高，為BMS中高精度的算法進一步開發(fā)奠定了基礎(chǔ)，能夠有效提高SOC，SOH，SOF等關(guān)鍵參數(shù)的精度大大提高電池的使用壽命和安全性。