多屬性逆向同步增價拍賣模型及最優投標策略

冉茂盛,黃 俊,蔣衛艷

(1.重慶大學經濟與工商管理學院,重慶400030;2.香港理工大學建筑及房地產學系,中國香港999077)

1 引 言

逆向拍賣又被稱為采購拍賣,是一種存在唯一賣方(采購商)和多個競爭性買方(供應商)的拍賣形式.隨著互聯網的普及和電子商務的發展,逆向拍賣機制已經被越來越廣泛的用于企業的電子采購[1].由于采購商在進行電子采購時,除了關心物品的提供價格外,往往還會考慮物品的質量、交貨期和售后服務等其他非價格屬性,例如在飛機采購合同中,產品的質量、交貨期等與價格處于同等重要的位置.多屬性逆向拍賣日漸成為電子采購的主流形式,并成為拍賣理論研究的熱點之一.

早期的文獻主要研究單物品的多屬性拍賣.Che[2]基于投標人成本獨立的前提,提出了二維多屬性拍賣模型,而Branco[3]則研究了基于投標人成本相互關聯前提的二維多屬性拍賣模型.在Che的研究基礎上,David[4,5]進一步將模型擴展到任意多維屬性的情形,構建了一般意義上的多屬性拍賣模型.孫亞輝等[6]對David的模型進行改進,使其更符合現實且具有更廣泛的適用性.曾憲科等[7]在模型中加入了質量屬性最低值的約束,建立了基于非對稱投標人的多屬性英式逆向拍賣模型,并得出了供應商的均衡投標策略.此外,王明喜等[8]通過對采購商的評分函數進行修改,建立了基于簡單加權法的多屬性逆向拍賣模型,從而解決了價格屬性和質量屬性量綱不統一和數值不可比的難題.

而現實中的采購商往往一次性采購多個物品,且物件間又具有一定的互補性,此時單物品的多屬性拍賣機制已不能滿足實踐的要求.于是,此后的研究將多屬性拍賣從單物品情形拓展到多物品情形.在組合效應存在的前提下,關于多物品多屬性拍賣的文獻主要研究以下兩種拍賣機制:1)同步二級價格密封拍賣(simultaneous sealed-bid second-price auction,SSA)機制.在Krishna等[9]包含兩類供應商的單屬性SSA拍賣模型的基礎上,黃河等[10]將多屬性拍賣引入SSA機制,建立了采用SSA機制的多物品多屬性逆向拍賣模型,并分析了物品組合效應對供應商投標策略的影響.2)動態拍賣機制.在另一篇論文中,黃河等[11]基于組合拍賣規則,設計了一種多屬性逆向拍賣的動態機制,并分析了投標者的均衡投標策略.姚升保[12]則在Zhang等[13]研究的基礎上,將多輪逆向拍賣機制(iterative multi-attribute multi-unit reverse auction,IMMRA)引入到多屬性拍賣中,研究了采購商信息披露政策對拍賣的影響.

上述關于多物品多屬性拍賣的文獻,均未涉及同步增價拍賣(simultaneous ascending auction,SAA)機制下的多屬性拍賣.同步增價拍賣是單物品英式拍賣在多物品情形下的推廣,該機制中的多個物品同時進行公開叫價,直到所有物品的出價均不變時拍賣結束,物品的最高出價人獲得相應物品[14].SAA機制作為一種重要的多物品拍賣機制,由于可操作性強及便于投標者對標的物的比較選擇,被各國政府大量應用于特定市場的牌照拍賣中,例如美國聯邦通訊委員會(FCC)主要使用SAA機制來拍賣無線電頻譜拍照[15].SAA機制還被用于采購拍賣中,現實中的采購商除關心物品的價格外,往往還會考慮物品的其他非價格屬性,為了對該情形下的多物品拍賣進行分析,有必要研究多屬性逆向SAA機制及其均衡策略.基于此,本文將同步增價拍賣機制引入到存在組合效應的多屬性逆向拍賣中,建立了基于兩類非對稱供應商的多屬性逆向同步增價拍賣模型.從供應商期望收益最大化角度,給出了兩類非對稱供應商的均衡投標(包括價格投標和非價格投標)策略,并驗證了均衡最高得分關于組合效應單調遞增.與黃河等[10,11]的密封多物品多屬性拍賣機制不同,本文將一種應用最普遍的公開多物品拍賣機制—–SAA機制引入到多屬性拍賣中去,從而進一步拓展了現有的多物品多屬性拍賣理論[10-12].從機制設計的角度,一方面將Zheng[16]和Goeree等[17]的SAA機制由單屬性拓展到了多屬性,另一方面將黃河等[10]的多屬性逆向拍賣由SSA機制拓展到了SAA機制.此外,由于SAA機制在現實中的廣泛應用,研究作為其拓展的多屬性逆向SAA機制,有利于指導現實的多物品多屬性電子采購實踐.

為此本文構建了多屬性逆向同步增價拍賣模型,在推導出兩類供應商的均衡非價格屬性投標的基礎上,得出了地方供應商的均衡價格投標策略,然后運用逆向遞推法,進一步的分析給出了全局供應商的均衡價格投標策略,并對組合效應進行了比較靜態分析.最后,通過在線拍賣的實例給出了兩類供應商均衡投標策略的計算步驟及結果.

2 多屬性逆向同步增價拍賣模型

多屬性逆向同步增價(分)拍賣是多屬性逆向英式拍賣由單物品向多物品的擴展.在多屬性逆向同步增價拍賣中,采購商向多個潛在供應商采購n個物品,n個提供物品的競拍同時進行.采購商對物品的要求包含價格屬性和非價格屬性,物品的分配由采購商制定的評分函數來決定.此時,供應商之間通過公開報分對提供物品的機會進行競爭,物品由獲得最高得分的供應商提供,因此該拍賣又可以被稱為多屬性逆向同步增分拍賣.

本文考慮唯一的采購商采購兩個物品.拍賣中有兩類供應商,第一類供應商只對提供兩個物品中的某一個有興趣(有能力),稱為地方供應商;第二類供應商對提供全部兩個物品均有興趣,且同時提供兩個物品產生的價值大于分別提供這兩個物品分別產生的價值之和,稱為全局供應商.此時,同時提供兩個物品給全局供應商帶來的額外收益稱為物品的組合效應,用α表示.

2.1 模型的基本假設

為簡化分析,除假設物品的拍賣最小加分幅度無窮小之外,還建立了如下假設:

假設1采購商購買的物品具有1+m個屬性,價格屬性為p,其余m個相互獨立的非價格屬性用qj表示,j=1,2,...,m.模型中的非價格屬性為為效益型屬性,即屬性值越大表明產品質量越高;而對于成本型屬性,可運用取倒數或極差變換等方法轉化為效益型屬性.

假設2拍賣中的所有參與人都是風險中性的,且滿足個體理性條件.因此,供應商選擇在自身效用大于零時參加拍賣,且采供雙方的效用均具有可加性.

假設3對任意非價格屬性qj,采購商的效用遞增,而邊際效用遞減;供應商的生產成本和邊際生產成本均是遞增的.

假設4供應商對所感興趣物品的成本參數在區間上獨立同分布,其分布函數及相應的密度函數分別為F(x)和f(x),是公共知識,且.特別的,由于地域的限制,地方供應商只能提供某一個物品;全局供應商可同時提供兩物品,且對兩物品的成本參數相同,這與Krishna等[9]的假設相同.

假設5拍賣中有兩個地方供應商和一個全局供應商,全局供應商同時提供兩個物品時獲得的額外收益即為組合效應,用α表示,為正常數.這里從收益角度來理解組合效應,但若從成本角度看,組合效應可被視為成本的減少,即供應商提供兩個物品可以享受規模經濟.然而,無論是理解為收益的增加還是成本的減少,都不會對最終的分析產生影響.

假設6供應商的類型為共同知識,而組合效應及成本參數為相應供應商的私人信息,其他供應商只知道其分布函數.不同于Krishna等[9]和Albano等[18]關于α為公共知識的假設,這里更具一般性的假設α為全局供應商的私人信息.

2.2 采購商的效用函數與評分函數

在多屬性拍賣中,采購商以價格p購買非價格屬性值為q1,q2,...,qm的物品時,其獲得的效用為

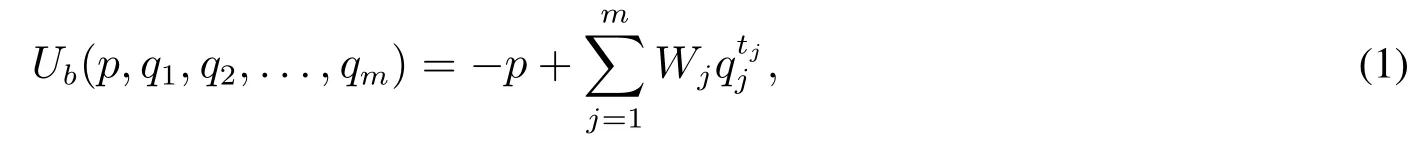
其中Wj為采購商賦予非價格屬性qj的權重,表示其對qj的偏好程度,且Wj＞0;tj為采購商賦予非價格屬性qj的冪次,則0＜tj＜1表示采購商邊際效用關于qj遞減,與假設3一致.Wj和tj為采購商的私人信息.

假設采購商對不同物品的Wj和tj相同.用pi表示采購商購買物品i的價格,則采購商購買兩個物品時的效用為.

評分函數是由采購商制定并在拍賣前向所有潛在供應商公布的獲勝者確定及物品分配方案,由價格屬性p和非價格屬性q1,q2,...,qm構造而成.采購商公布的評分函數可能偏離其真實效用,其評分函數為

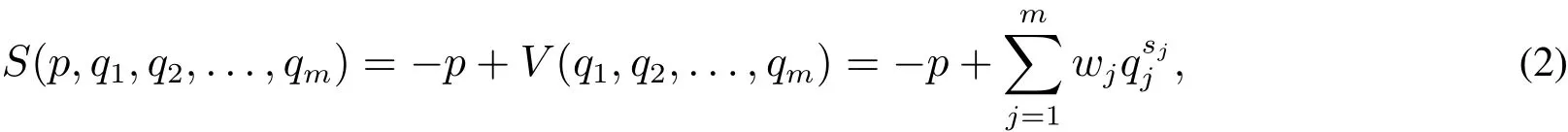
2.3 兩類供應商的效用函數

若成本參數為θ的供應商以價格p及非價格屬性值q1,q2,...,qm獲得提供物品的機會,則其效用函數為

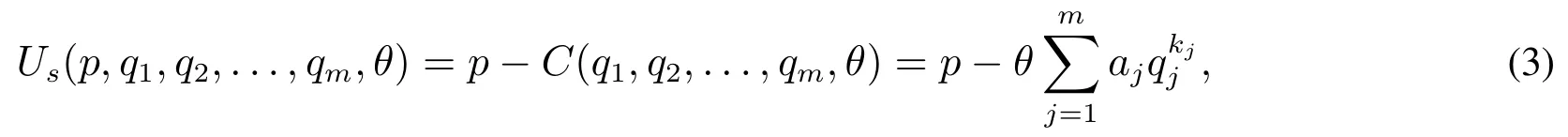
用pi表示全局供應商對物品i的價格屬性投標,由于同時提供兩個物品可獲得額外收益α,故此時全局供應商獲得的總效用為.

2.4 多屬性逆向同步增價拍賣機制描述

首先,由采購商公布拍賣的規則,包括所拍賣物品包含的價格屬性和非價格屬性(質量)、物品數量、評分函數和結束規則等.

然后,是供應商競分及獲勝者確定階段.以兩個地方供應商和一個全局供應商的情形為例進行說明.兩個物品的采購同時進行,兩地方供應商分別參與相應物品的采購競標,而全局供應商同時參與兩個物品的采購競標.采用公開叫分的方式,兩類供應商根據評分函數計算出的得分進行競爭,直至兩物品的采購中都僅剩唯一供應商時采購結束.僅剩的供應商獲得提供對應物品的合同.

最后,每個物品的最終獲勝者為相應拍賣中得分最高的供應商,獲勝者按照其投標的價格屬性值和非價格屬性值配置出售物品.

3 兩類供應商非價格屬性均衡投標策略

在多屬性逆向同步增價拍賣中,供應商的投標策略由價格屬性值p和非價格屬性值q1,q2,...,qm構成,供應商根據評分函數計算出的得分進行投標.不同于密封拍賣的一次性報價(分),本文的模型為公開拍賣形式,供應商通過互相競分直至最高得分者勝出,此時供應商的均衡策略就意味著其最優退出水平.在給定采購商的評分函數和供應商效用函數的前提下,供應商的目標為選擇合適的價格屬性值p及非價格屬性值q1,q2,...,qm,計算得出可接受的最高得分以最大化其期望效用.

在非價格屬性的投標方面,全局供應商和地方供應商是對稱,下面的定理給出了兩類投標者的非價格屬性投標策略.

定理1給定采購商的評分函數和供應商的效用函數,在第一得分拍賣中,供應商的最優非價格屬性值q1?,q2?,...,qm?獨立于價格屬性p和其他供應商的策略,為.進一步的,由一階條件可以得到

證明運用反證法.給定供應商成本參數θ,假設存在至少一個非價格屬性值使投標組合(p,q1,q2,...,qm)最大化供應商期望效用π(p,q1,q2,...,qm,θ).再構造一個投標策略組合(p′,q?1,q?2,...,q?m),其中p′=p+V(q?1,q?2,...,q?m)-V(q1,q2,...,qm),故S(p,q1,q2,...,qm)=S(p′,q?1,q?2,...,q?m).此時,如果證得構造的策略組合(p′,q?1,q?2,...,q?m)帶給供應商的效用大于策略組合(p,q1,q2,...,qm)的效用,那么就與假設矛盾,從而原命題成立,即最優非價格屬性qj=q?j.

下面只需證策略組合(p′,q?1,q?2,...,q?m)帶給供應商的效用大于策略組合(p,q1,q2,...,qm).用G(S)表示供應商得分為S時獲勝的概率.此時,供應商的期望效用為

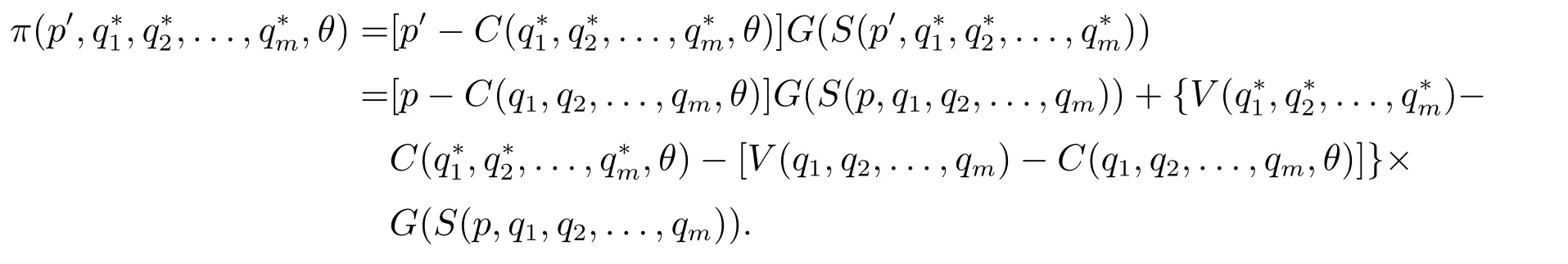
由q?j(θ)的定義,可知V(q?1,q?2,...,q?m)-C(q?1,q?2,...,q?m,θ)＞V(q1,q2,...,qm)-C(q1,q2,...,qm,θ).于是,有

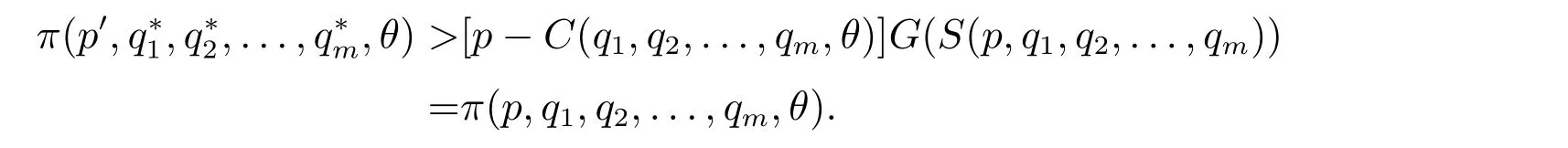
因此,原命題成立.再由一階條件,可得式(4)成立. 證畢.

定理1的證明與Che[2]和曾憲科等[7]的方法類似.由定理可以看出,供應商的非價格屬性投標在每輪投標中固定不變且不受組合效應影響.而由于全局供應商對兩個物品成本參數相同,所以其非價格屬性投標策略也相同.為進一步分析,給定由定理1所確定的非價格屬性均衡策略,均衡時采購商估值函數可表示為V(θ)≡V(q?1,q?2,...,q?m),供應商的成本函數和得分函數可分別表示為C(θ)≡C(q?1,q?2,...,q?m,θ)和S(θ)≡S(p,q?1,q?2,...,q?m).

4 兩類供應商價格屬性均衡投標策略

組合效應對全局供應商均衡投標策略的影響主要體現在價格屬性投標方面,全局供應商和地方供應商在價格屬性投標方面不再對稱.在多屬性逆向拍賣中,由于供應商的非價格屬性投標均為固定不變的,供應商之間的競爭本質上是價格屬性投標的競爭,故這里的價格屬性均衡投標策略是指供應商的價格屬性投標最低值.

4.1 地方供應商價格屬性均衡投標

地方供應商的占優策略為在其效用等于零時退出,這是由于:對于使得效用為正的價格屬性值,地方供應商是有利可圖的,故其會繼續參加投標;對于使得效用為負的價格屬性值,理性的地方供應商不會選擇參與拍賣,所以在效用等于零時退出,此時的均衡投標策略滿足激勵相容和個體理性條件.由于非價格屬性投標固定不變,由此可以確定出其價格屬性投標策略.于是,可以得到如下定理.

定理2給定采購商的評分函數和供應商的效用函數,在第一得分拍賣中,物品相應地方供應商的均衡價格屬性值(最低出價水平)為

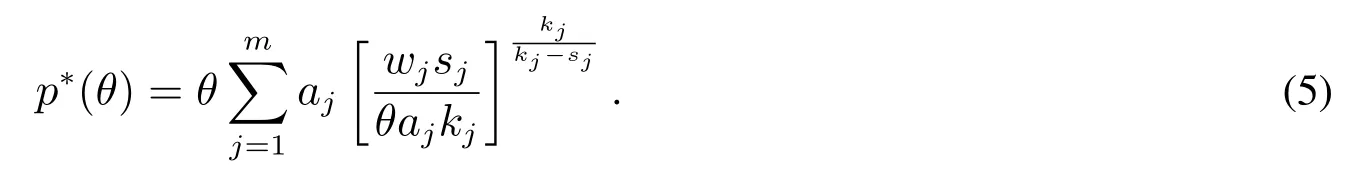
進一步地,地方供應商均衡投標的最高得分為

證明由于地方供應商在最低出價水平時的效用為零,即

推論1在第一得分拍賣中,地方供應商的均衡價格屬性值p?(θ)和均衡投標的最高得分S?(θ)關于成本參數θ嚴格單調遞減.

證明在式(5)中,對θ求導,可得

其中kj-sj＞0.所以,p?(θ)關于成本參數θ嚴格單調遞減.在式(6)中,對θ求導,可得

即S?(θ)關于成本參數θ嚴格單調遞減. 證畢.

由定理2可以看出,該機制中地方供應商價格屬性投標策略與多屬性逆向英式拍賣模型中的相同,最小加分幅度為D時,即為曾憲科等[7]得出的結論.此外,由地方供應商最高得分S?(θ)=V(θ)-C(θ)及推論1,得V′(θ)-C′(θ)＜0.

4.2 全局供應商價格屬性均衡投標

組合效應的存在使得全局供應商的價格屬性投標策略復雜化,下面對此進行分析.由于供應商的最高得分決定了拍賣的結果,而由推論1可知成本參數與非價格屬性均衡投標及地方供應商的最高得分一一對應,故可通過分析全局供應商均衡投標最高得分及對應水平的局部供應商成本參數來推出其價格屬性均衡投標.

用S?(1)(θ)和p?(1)(θ)分別表示僅剩一個地方供應商(或物品)時私人成本為θ的全局供應商的均衡投標的最高得分和價格屬性值;用S?(2)(θ)和p?(2)(θ)分別表示剩余兩個地方供應商(或物品)時全局供應商的均衡投標的最高得分和價格屬性值.用θ(1)表示以分數水平S?(1)(θ)為均衡最高得分的地方供應商成本參數,有S?(1)(θ)=S?(θ(1));用θ(2)表示以分數水平S?(2)(θ)為均衡最高得分的地方供應商成本參數,有S?(2)(θ)=S?(θ(2)).根據S?(θ)關于θ遞減,有θ(1)≡S?-1(S?(1)(θ))和θ(2)=S?-1(S?(2)(θ)).用θmin表示兩個地方供應商中的較小私人成本,用θmax表示兩個地方供應商中的較大私人成本.用Fn(θ|p)=[F(θ)/F(p)]n表示n個地方供應商中的最大私人成本小于水平p前提下,該最大私人成本小于θ的條件概率,n=1,2.

從決策順序角度,全局供應商的競拍決策分為兩個階段:在第一階段,若S?(2)(θ)＜S?(θmax),則全局供應商在分數達到S?(2)(θ)時退出拍賣;若S?(2)(θ)≥S?(θmax),則以分數S?(θmax)獲得提供該物品的機會并進入拍賣的第二階段.在第二階段,若S?(1)(θ)＜S?(θmin),則全局供應商在分數達到S?(1)(θ)時退出拍賣;若S?(1)(θ)≥S?(θmin),則以分數S?(θmin)獲得提供該剩余物品的機會.

定理3給定采購商的評分函數和供應商的效用函數,假定φ(θ,θ(2))關于θ(2)在[θ,θ]內為凸函數,在第一得分拍賣中,該逆向拍賣機制存在一個精煉貝葉斯均衡.全局供應商第一階段的均衡投標最高得分S?(2)(θ)=S?(θ?(2)),相應的均衡價格屬性投標p?(2)(θ)=V(θ)-S?(2)(θ).其中,

而θ(+2)為方程的唯一根或兩根中的較大者;全局供應商第二階段均衡投標最高得分S?(1)(θ)=S?(θ?(1)),相應的均衡價格屬性投標p?(1)(θ)=V(θ)-S?(1)(θ).其中

而θ+(1)為方程S?(θ(1))=V(θ)-C(θ)+α的唯一根.

證明運用逆向遞推法,先看第二階段全局投標人的均衡策略.此時,全局供應商已經是第一件物品的獲勝者.成本參數為θ的全局供應商在S?(1)時退出,其對S?(1)(θ)選擇可轉化為選擇θ(1)以最大化期望收益

上式對θ(1)求偏導數,得到以下一階條件

當S?(θ(1))=V(θ)-C(θ)+α時,π1(θ,θ(1)|θmax)取到最大值,用θ+(1)表示方程的解.由于

故方程的解θ(+1)唯一.由S?(θ(1))的單調性及,存在唯一使得成立.此時,對所有,全局供應商選擇最大化其期望收益;對所有,選擇最大化其期望收益.于是,由θ?(1)可得全局供應商的均衡投標最高得分.再由評分函數式(2),可得全局供應商在第二階段的均衡價格屬性投標.

再看第一階段全局投標人的均衡策略.第一階段全局供應商同時參加兩件物品競拍.在地方供應商私人成本均小于p前提下,全局供應商在S?(2)(θ)時退出拍賣,其對S?(2)選擇可轉化為對θ(2)選擇以最大化期望收益

上式對θ(2)求偏導數,得到以下一階條件

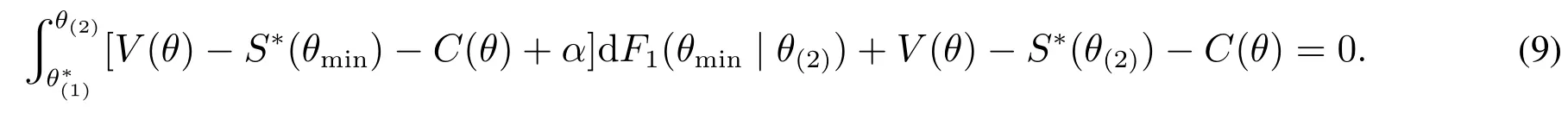
由φ(θ,θ(2))關于θ(2)的凹凸性,可知方程φ(θ,θ(2))=0最多存在兩個根,用表示方程的唯一根,或者兩根中的較大者.如果方程存在唯一的根,則為局部最優點;如果方程存在兩個根,由凸性假設可知為凹函數,而的導數在方程的較大根處取值為負,此時也是局部最優點.為得到全局最優解,再比較邊界解和內解.本文采用類似于Krishna等[9]和黃河等[10]的方法,定義.由于

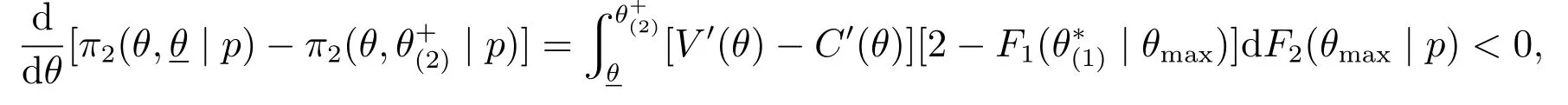
從定理3的結論中可以觀察到:首先,均衡價格屬性投標p?(1)獨立于全局投標人在第一階段的投標策略,而只取決于其成本系數和組合效應;其次,p?(2)不但取決于其成本系數和組合效應,還與私人成本系數θmin的分布有關;最后,私人成本系數θmax不影響全局投標人的均衡價格屬性投標p?(1)和p?(2),但是只有當時拍賣才會進入第二階段.

推論2給定采購商的評分函數和供應商的效用函數,對所有可得

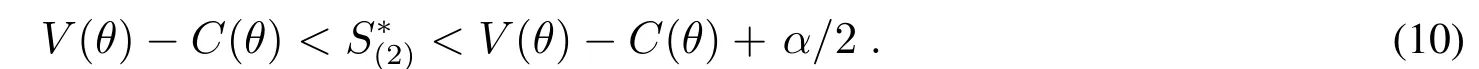
證明對,由式(9),有

另一方面,由于

所以S?(2)＜V(θ)-C(θ)+α/2. 證畢.

4.3 兩類供應商投標策略的比較靜態分析

以上部分均基于給定的α來分析兩類供應商的投標策略,下面分析α變化時供應商均衡策略變化情況.

對于地方供應商,由定理2可知,組合效應α對其均衡策略沒有影響.而對于全局供應商,由定理3可知,全局供應商在第一階段和第二階段的均衡投標策略均受α影響.于是,下面定理分析了組合效應對全局投標人均衡策略的影響.

定理4給定采購商的評分函數和供應商的效用函數,在第一得分拍賣中,全局供應商在兩階段的均衡投標最高得分S?(1)(θ)和S?(2)(θ)關于組合效應α單調遞增,均衡投標價格屬性值p?(1)(θ)和p?(2)(θ)關于組合效應α單調遞減.

證明由定理3,對于第二階段,在上,有,顯然其關于α遞增;而在上,為常數,由于,所以當α增大時,隨之增大.也就是說,隨著α增大,在上的關于α遞增,同時隨之增大,此時會使更大區域內的均衡投標最高得分為常數.同理,由,可以證得隨α遞減.

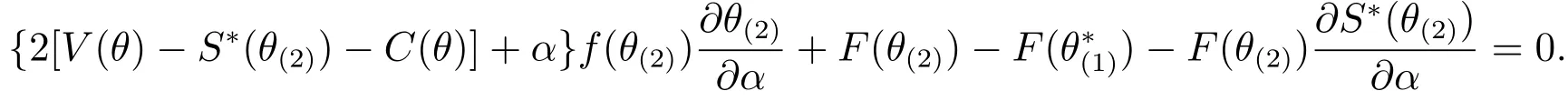
利用鏈式法則,上式可整理為

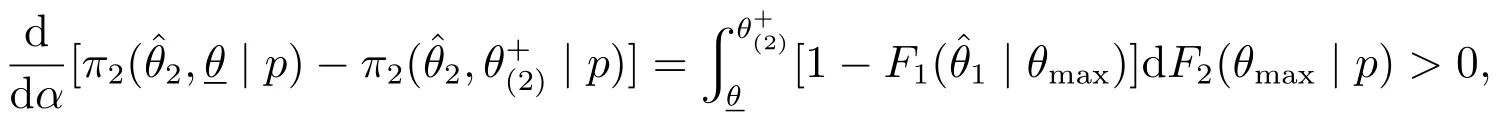
5 拍賣案例分析

假定某采購商通過逆向多屬性同步增價拍賣機制在兩相鄰地域采購兩件物品,該拍賣通過在線拍賣系統進行.地方供應商只需在系統中輸入其成本參數,而全局供應商在系統中輸入其成本參數和組合效應值,均衡投標的屬性值由相應命題推導出的公式計算得出,此時投標人可利用在線拍賣系統的代理投標功能進行自動投標,并由該系統決定最終物品的分配和支付.

在該拍賣機制中,除所采購物品的價格屬性外,采購商還關心物品所對應的兩個非價格屬性q1和q2.假定采購商公布的評分函數的參量w1=1,w2=2,s1=s2=0.5與其效用函數中的參量一致.拍賣中有兩個地方供應商和一個全局供應商,其成本函數中的參量為a1=0.5,a2=0.25,k1=k2=1.5,兩類供應商的成本參數在區間[0.2,0.6]上服從均勻分布.此時,.容易驗證,函數φ(θ,θ(2))滿足凸性要求.

對于給定的θ,根據定理1可以計算出兩類供應商的均衡非價格屬性值q?1和q?2;根據定理2可以計算出地方供應商的均衡價格屬性值p?和最高退出得分S?.分別給定θ為0.2,0.3,0.4,0.5,0.6,局部供應商的均衡非價格屬性值、最低價格屬性值和最高得分的計算結果如表1所示.

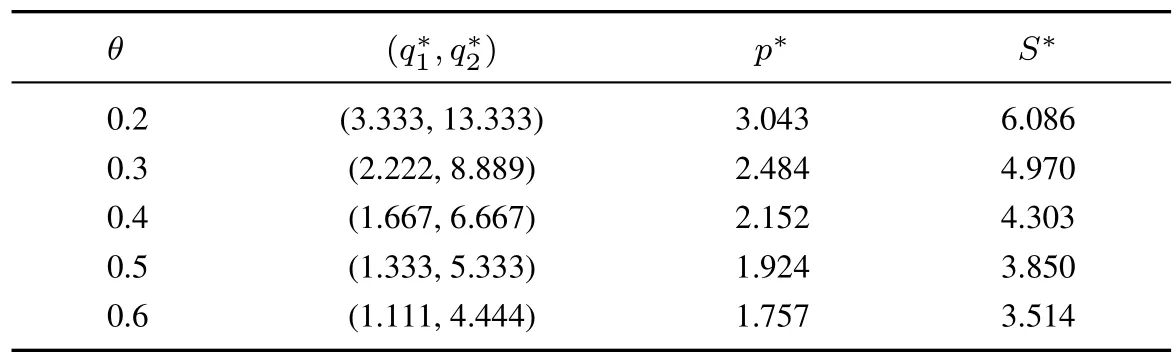
表1 地方供應商的均衡投標策略及最高退出得分Table 1 The local bidders’equilibrium bidding strategies and optimal drop–out scores

再給定α的取值,根據定理3可以計算出全局供應商在兩階段的均衡價格屬性值以及相應的最高退出得分.具體的計算步驟如下:

步驟1根據確定分界點;

步驟2在上,有,根據,計算出.在上,根據計算出S?(1)(θ)并求出唯一的根θ(+1),確定;

步驟3根據計算出的S?(1)(θ),由p?(1)(θ)=V(θ)-S?(1)(θ)計算出p?(1)(θ);

步驟4再計算拍賣第一階段的內解.已知θ?(1)及由供應商分布函數得到的條件分布函數,根據式(9)計算出θ(+2)為方程的唯一根或者兩根中的較大者.再將不同θ所對應的期望收益π2(θ,θ(+2)|p)與邊界點處的期望收益比較,從而確定出分界點;

步驟5在上,確定,在上,確定,從而計算出S?(2)(θ),然后再由p?(2)(θ)=V(θ)-S?(2)(θ)計算出p?(2)(θ).

下面的表2和表3給出了當α分別為0.5和1.0時,θ為0.2,0.3,0.4,0.5,0.6時,全局供應商在兩階段的均衡非價格屬性值、最低價格屬性值和最高得分的計算結果.

表2 當α=0.5時全局供應商的均衡投標策略及最高退出得分Table 2 The global bidder’s equilibrium bidding strategy and optimal drop-out score when α equals 0.5

表3 當α=1.0時全局供應商的均衡投標策略及最高退出得分Table 3 The global bidder’s equilibrium bidding strategy and optimal drop-out score when α equals 1.0

比較表2和表3中的數據,可以看出:組合效應α越大,全局供應商在兩階段的均衡投標最高得分和越大,而最低投標價格屬性值p?.(1)和p?(2)越小,這些結果與文中的定理相符.

下面以α=0.5情形為例進行說明.假定全局供應商的成本參數θ=0.5,兩個地方供應商成本參數0.2≤θmin≤θmax≤0.6,查表可知:當θmax＜0.482時,全局供應商退出拍賣,兩個地方供應商贏得拍賣且支付分數均為S?(0.482)=3.921;當θmax≥0.482時,全局供應商贏得提供一個物品的機會,其支付分數為S?(θmax),并進入拍賣第二階段.在第二階段,當θmin＜0.392時,全局供應商退出對第二個物品的競拍,該階段地方供應商的支付分數為S?(0.392)=4.350;當θmin≥0.392時,全局供應商繼續贏得提供第二個物品的機會,其支付分數為S?(θmin),此時全局供應商獲得了提供兩個物品的機會.

6 結束語

在多屬性拍賣中,多物品采購拍賣的相關研究尚不充分.基于存在兩類非對稱供應商的前提,本文將同步增價拍賣(SAA)引入多屬性逆向拍賣中,設計了一種多物品多屬性逆向拍賣機制,即多屬性逆向同步增價拍賣機制.從供應商的角度出發,在研究了兩類供應商的非價格屬性均衡投標策略的基礎上,分別對兩類供應商的價格屬性投標策略進行分析.針對公開競分的拍賣形式和拍賣中存在的組合效應,將全局供應商的投標決策分為兩個階段進行研究,得出了該拍賣機制下的精煉貝葉斯均衡,并對影響策略的組合效應作了比較靜態分析.最后,通過拍賣實例給出了兩類供應商均衡投標策略的計算步驟,并對物品的分配和支付作了示例,以便于該機制在現實采購拍賣中的運用.

本文的分析只是基于兩個物品的情形,運用類似的逆向遞推法,容易分析采購物品多于兩個的多屬性逆向同步增價拍賣模型.另外,本文的分析主要基于供應商視角,未來的研究可以從采購商的角度進行分析,研究采購商所采取的最優評分規則及對拍賣結果的影響[21].