永磁同步電機匝間短路-退磁耦合故障分析

王 歡，鄭安文，許小偉，王蘇娟，雷 鵬

(武漢科技大學，武漢 430074)

0 引 言

永磁同步電機是常用永磁電機之一，體積小、效率高、轉矩密度大和功率因數大是其顯著的優點。與傳統電機相比，永磁同步電機因自勵磁而無需電樞和滑環，減少了勵磁損耗、摩擦損耗和接觸電損耗，效率明顯提高[1]，因而被廣泛應用于混合動力汽車和純電動汽車等新能源汽車中，但由于其運行工況復雜、安裝空間狹小和散熱環境惡劣等缺點，導致使用中故障率較高[2]。就使用情況而言，永磁同步電機的常見故障主要分為單一故障和耦合故障兩類。

耦合故障即兩種或兩種以上故障同時存在，如匝間短路故障在故障發生早期不易被察覺，故障后會引起電機內部電磁場畸變，繼而引發永磁體退磁故障的產生，導致電機出現匝間短路和永磁體退磁同時存在的耦合故障情形[3]。如果不及時對電機故障做出相應處理，則會出現局部溫度過高，導致電機無法正常工作甚至被燒毀，不僅造成經濟損失，嚴重時還會威脅駕駛員的生命[4]。但是目前關于永磁同步電機故障分析的研究多數集中于單一故障的研究，對耦合故障的分析相對缺乏，因此對電機的耦合故障展開深入分析具有重要的現實意義。

單一故障則是指電機只存在一種故障類型，如匝間短路故障、永磁體退磁故障、轉子斷條和偏心故障等。現有的對單一故障的研究主要是在匝間短路故障、永磁體退磁故障和偏心故障等方面。文獻[5]以混合動力汽車用永磁同步電機為對象，研究其定子斷層故障，并指出該斷層在電流和電壓的作用下會產生特定的畸變；文獻[6]提出了一種基于模型的永磁同步電機匝間短路故障檢測與隔離的方法，根據狀態觀測者估計的定子電流和定子電流的差產生的殘余電流矢量(以下簡稱RCV)來實現故障檢測；文獻[7]以永磁同步電機的電氣故障研究為主體，分別通過MATLAB/Simulink和Ansoft對相間短路、單相接地、失磁故障和匝間短路故障進行仿真模擬，并提出小波分解和神經網絡相結合的故障診斷方法；文獻[8]以V形磁路結構的永磁同步電機為對象，分析了單個磁極的不可逆失磁對單槽反電動勢的影響，并推導出了任意單個磁極以及任意多個磁極的空載反電動勢的數學模型，該數學模型可應用于不同程度的失磁故障分析中。傳統的單一故障分析是建立在電機的數學模型基礎上，通過計算數據分析電機的故障，計算繁瑣且不能準確反映電機真實的工作狀態[9]。

通過對目前研究現狀的分析可知，多數研究人員采用仿真代替實驗來獲取電機正常及故障運行條件下數據。由于對退磁類耦合故障的實驗屬于破壞性實驗，本研究亦通過數學模型進行驗證，即在Ansoft Maxwell環境下建立永磁同步電機的二維物理模型，并進行瞬態磁場分析，準確獲得電機在空載和額定負載兩種工況下，正常運行情況以及各種不同耦合故障程度的電磁場分布及特征參數的性能曲線，再對相反電動勢進行傅里葉變換以建立判斷依據，旨在為電機耦合故障診斷提供一種簡潔有效的判斷依據。

1 電磁場及邊界條件分析

永磁同步電機定子上裝有繞組，轉子上裝有永磁體[10]。永磁體周圍會產生磁場，定子繞組有電流通過會產生電場，繼而電機會存在電場和磁場的耦合。

電磁場的求解通常歸結為求偏微分方程的解，主要研究沒有初始條件而只有邊界條件的定解問題；其分析一般采用位函數描述，而二維電磁場計算多采用磁矢位，以方便繪出磁力線分布并求出磁通[11]。

1.1 邊界條件及離散化

研究磁場問題一般用第一類和第二類邊界條件。第一類邊界條件是指邊界上的物理條件規定了物理量u在邊界Γ上的值:

u|Γ=f1(Γ)

(1)

第二類邊界條件則是指u的法向微商在邊界Γ上的值[12]:

(2)

二維電磁場為垂直于電機軸的平行平面場，平面場域Ω上的電磁場問題的邊界條件可表示:

(3)

式中：γ為磁阻率，γ=1/μ，μ為磁導率；A為磁矢位；Jz為源電流密度；Ht為磁場強度的切向分量；Γ1,Γ2分別為第一類邊界條件和第二類邊界條件[13]。

二維磁場只有x和y軸分量，表達式分別如下[14]:

(4)

則式(3)可等價:

(5)

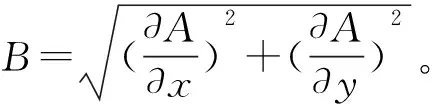
式(5)離散化后對應的非線性有限元方程組:

[k]A=p

(6)

令：{f(A)}=[k]A，按Taylor級數展開(略去高次項)后可得Newton-Lafayson迭代格式[14]:

Jk{ΔA}={Δp}

(7)

式中：{ΔA}={A}k+1-{A}k為磁位差；{Δp}=p-{f(A)}為剩余向量；Jk為第k次迭代時的Jacobin矩陣[13]，其單元計算公式:

(8)

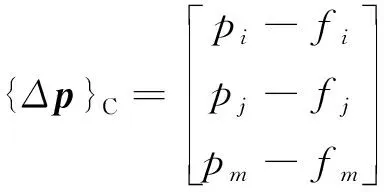
(9)

式中：

(10)

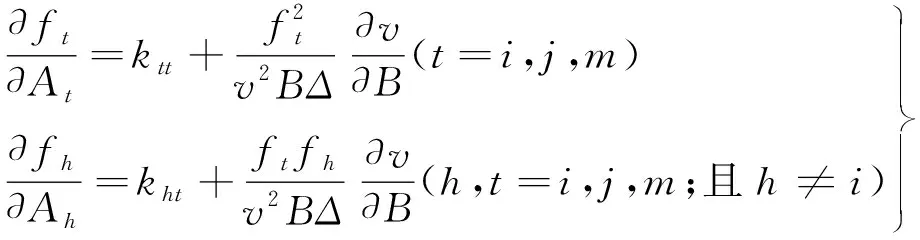
(11)

式中：Δ是離散為多個小單元時單個三角形單元的面積。

對磁化曲線的處理通常采用插值法，即用函數H=f(B)表示磁化曲線，每個插值節點Bi對應函數值為Hi(i=1，2，…，n)[12]。經線性插值法處理后可得:

顯然，獲得J和Δp，式(7)就可解得。

1.2 磁矢位的應用

(1)計算磁通

根據斯托克斯定理可得:

(13)

(2)計算感應電動勢:

(14)

(3)畫二維磁場

二維磁場中等A線即磁力線，證明如下。磁場中磁力線方程:

B×dl=0

(15)

而等A線就是A=常數的軌跡，其全微分是:

(17)

這與磁力線方程完全相同，說明等A線就是磁力線。

2 耦合故障關鍵特征量分析

這里耦合故障是指永磁同步電機匝間短路故障和永磁體退磁故障的耦合。

2.1 永磁同步電機正常模型及故障模型建立

根據電機的尺寸參數，在Ansoft中建立正常條件下的二維有限元全模型，如圖1(a)所示。永磁體呈雙層V形排列，材料為NdFe35；定子繞組為雙層分布短距繞組，節距為5，材料為銅；定、轉子鐵心材料為DW465-50，轉子軸材料為steel-1010，電機結構尺寸等基本參數如表1所示。

由于自適應網格剖分的單元格比較稀疏，會導致計算結果準確性不高，為提高計算精度選擇手動剖分方式。因永磁同步電機是對稱結構，為減少計算，選擇1/4模型進行二維瞬態磁場求解，圖1(b)為永磁同步電機1/4模型在初始時刻的網格剖分圖。

表1 電機主要參數

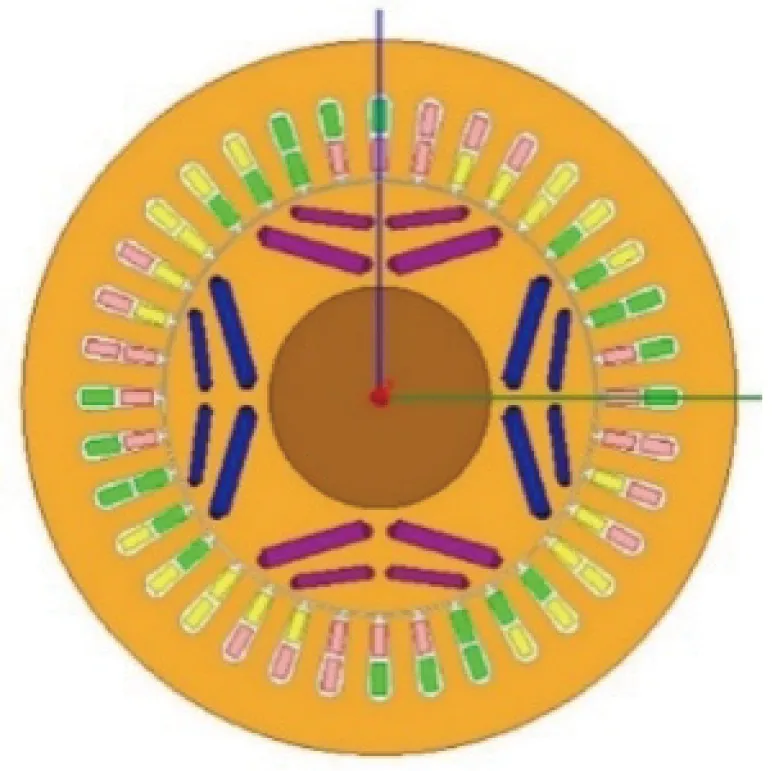
(a) 電機全模型

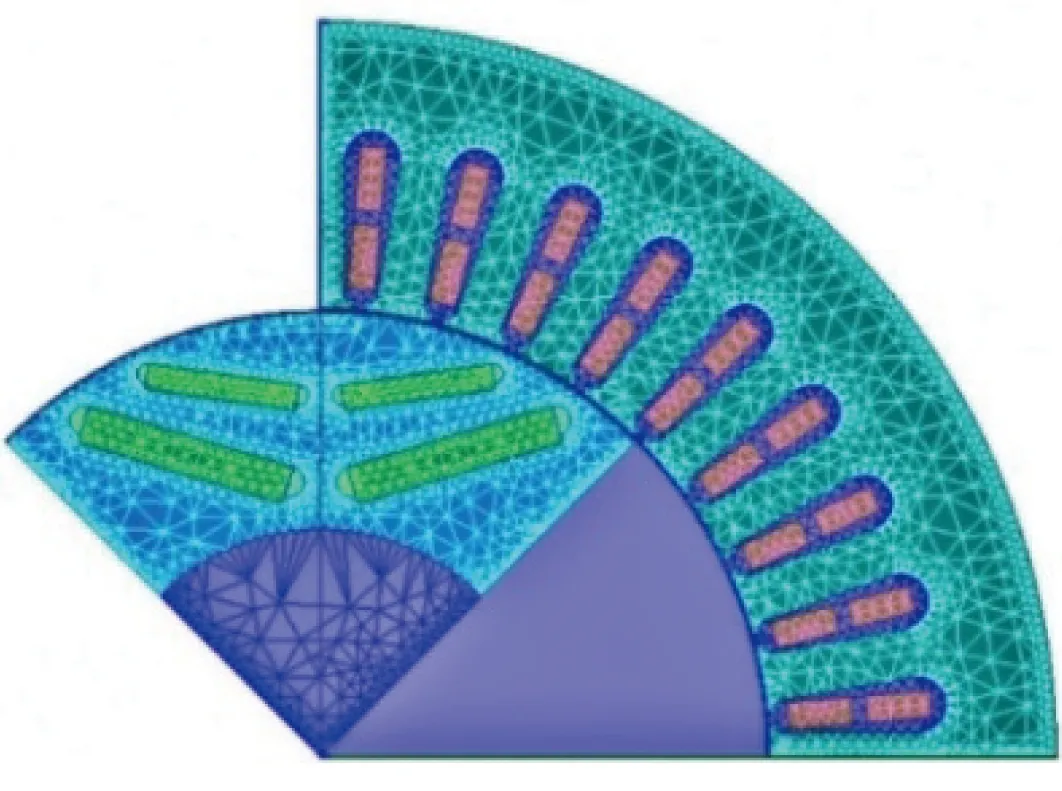
(b) 電機1/4模型在初始時刻

永磁同步電機常用的驅動電路類型有DC(直流)，PWM(光耦)，Sine Wave(交流正弦波)三種，本文采用Sine Wave供電，三相定子繞組各相差120°，如下所示：

(18)

以上建立的是電機正常條件下的有限元模型，而電機故障模型是在電機正常模型的基礎上，根據故障類型的機理而改變某些參數實現的，其具體分析過程如下。

設電機的正常相串聯匝數為N，A相未被短路的匝數為N1，A相被短路的匝數為N2，三者滿足[2]:

N1+N2=N

(19)

根據文獻[15]對永磁體材料退磁曲線的分析，得到電機發生退磁故障前后的磁場強度B與永磁體材料的性能參數Hc(永磁材料的矯頑力)和Br(剩余磁感應強度)的關系:

(20)

(21)

由式(19)和式(21)可得，在使用Ansoft軟件仿真分析過程中，建立永磁同步電機的匝間短路和永磁體退磁的單一故障模型只需分別改變繞組的匝數和永磁體的矯頑力；而建立耦合故障模型則需同時改變兩者的值，通過控制數值的大小分別建立故障程度為20%、40%、60%和80%的耦合故障模型。

2.2 耦合故障仿真及分析

對圖1(b)表示的電機1/4模型，分別在空載和額定負載工況下進行不同耦合故障程度的瞬態磁場分析，得到電磁場分布云圖和相關特征參數曲線圖，并將不同條件下的結果進行對比。

二維電磁場分布仿真結果主要包括磁感線分布云圖、磁密分布云圖和磁密矢量分布云圖等，由于不同云圖在不同故障程度下反映的結果相似，因此只需選擇其中一種作具體分析，將不同工況下不同故障程度的磁感線分布云圖作對比分析，如圖2所示。

(a) 無故障空載工況

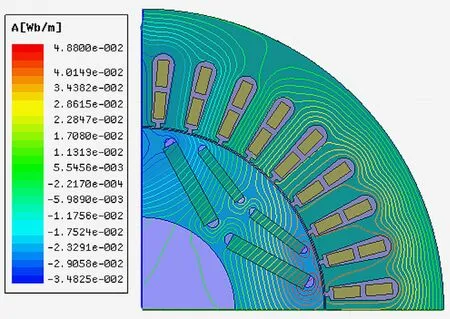
(b) 無故障額定負載工況

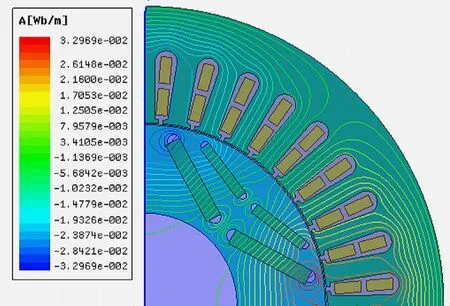
(c) 20%故障空載工況

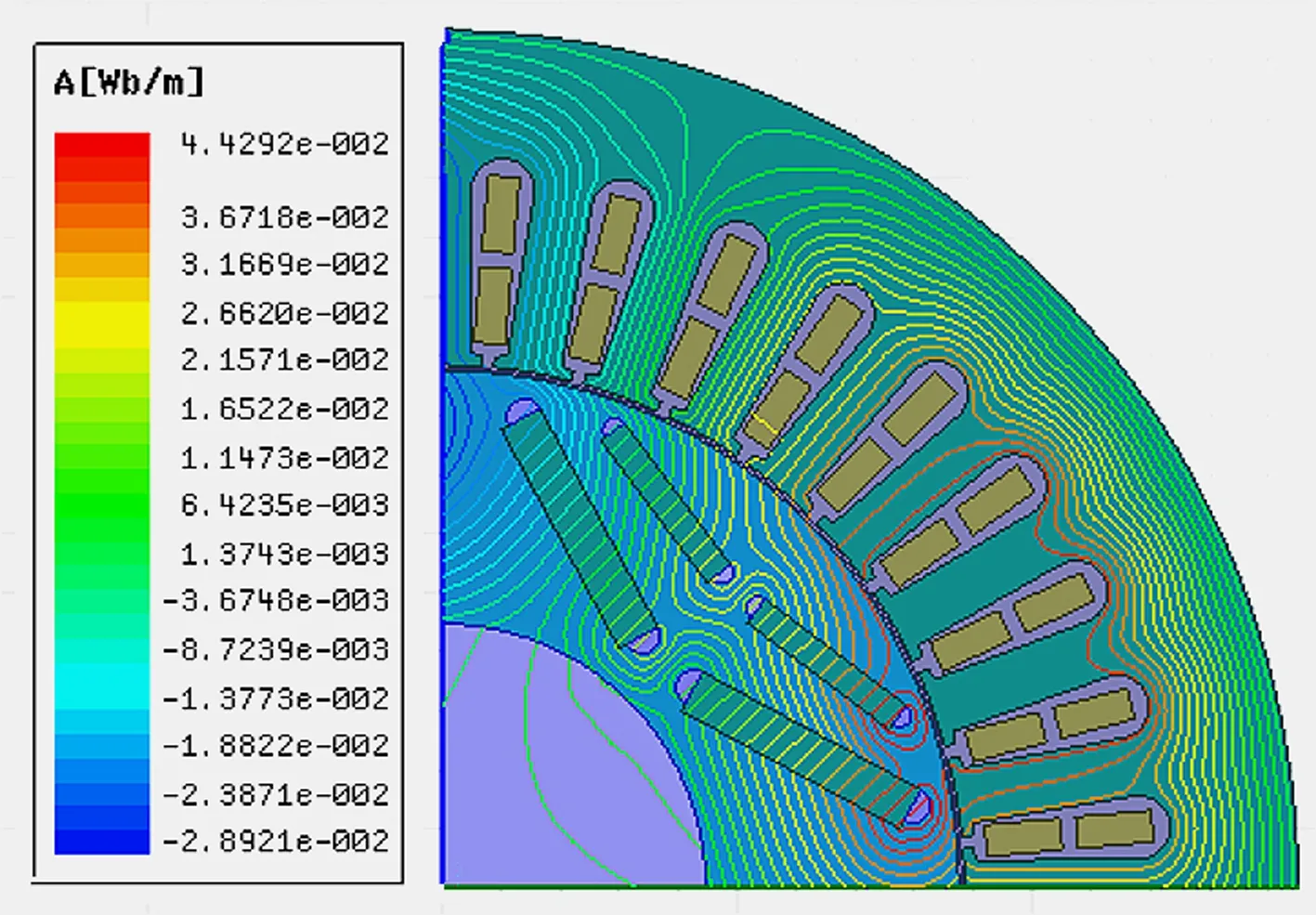
(d) 20%故障額定負載工況

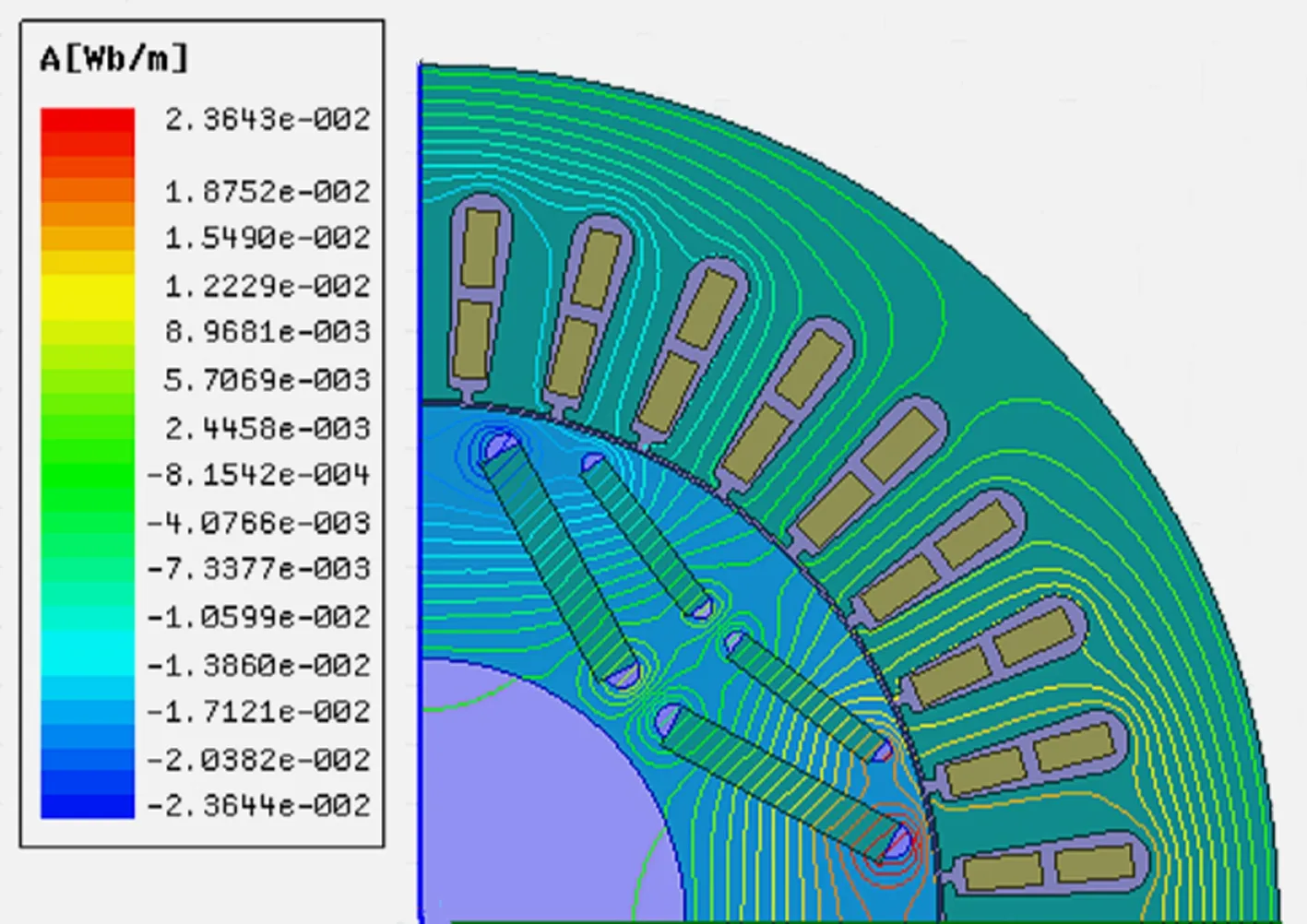
(e) 40%故障空載工況

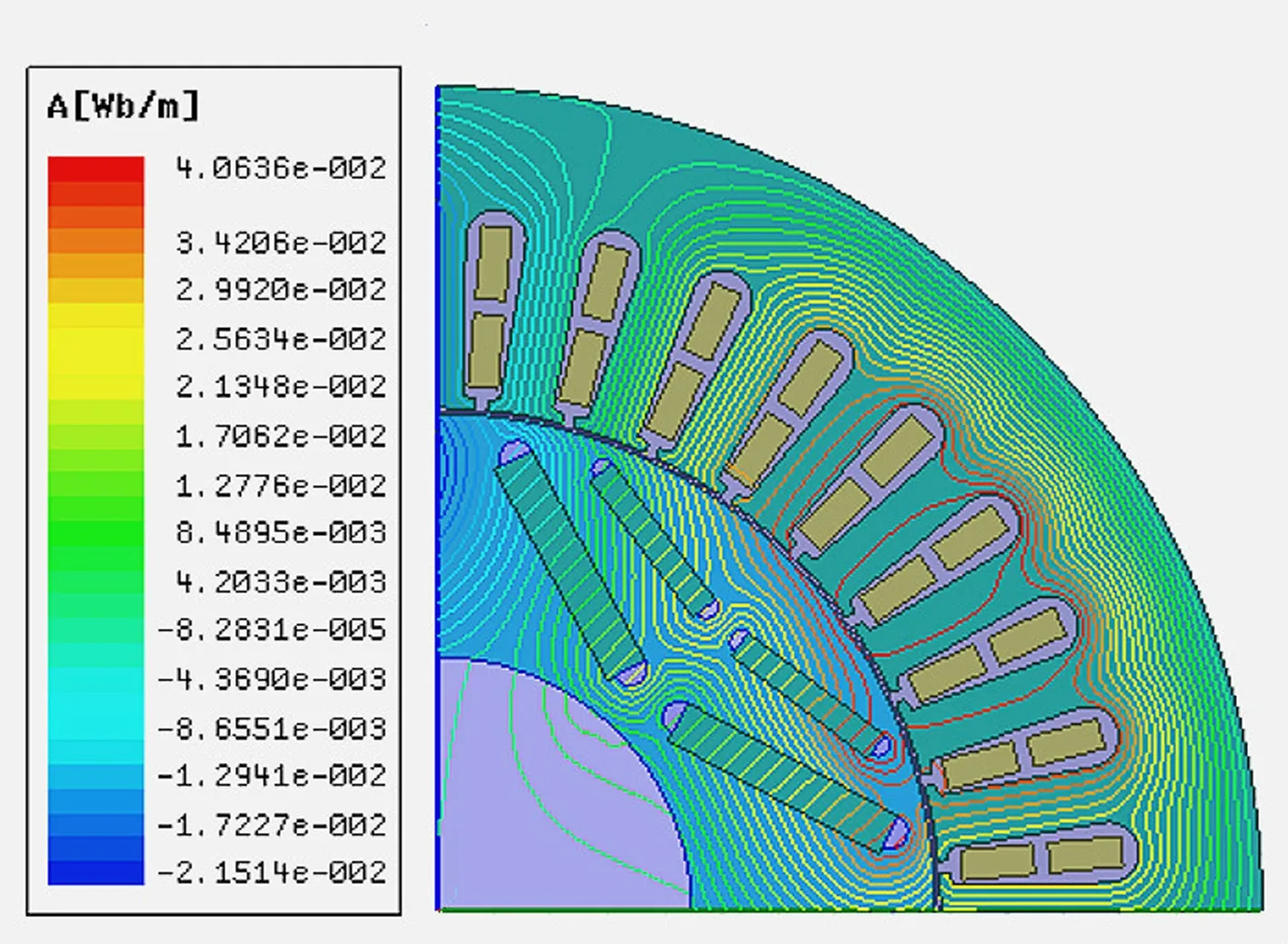
(f) 40%故障額定負載工況

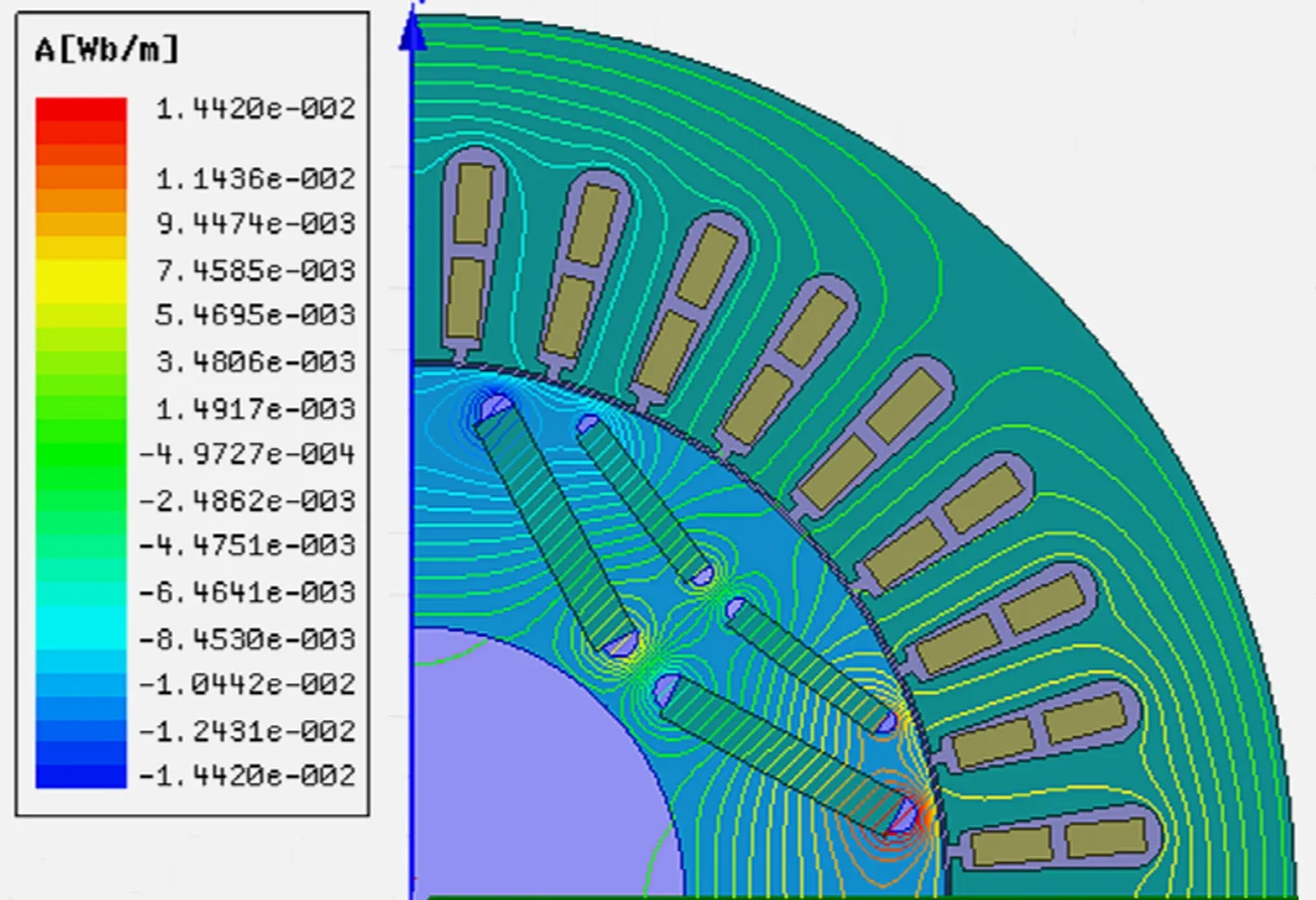
(g) 60%故障空載工況

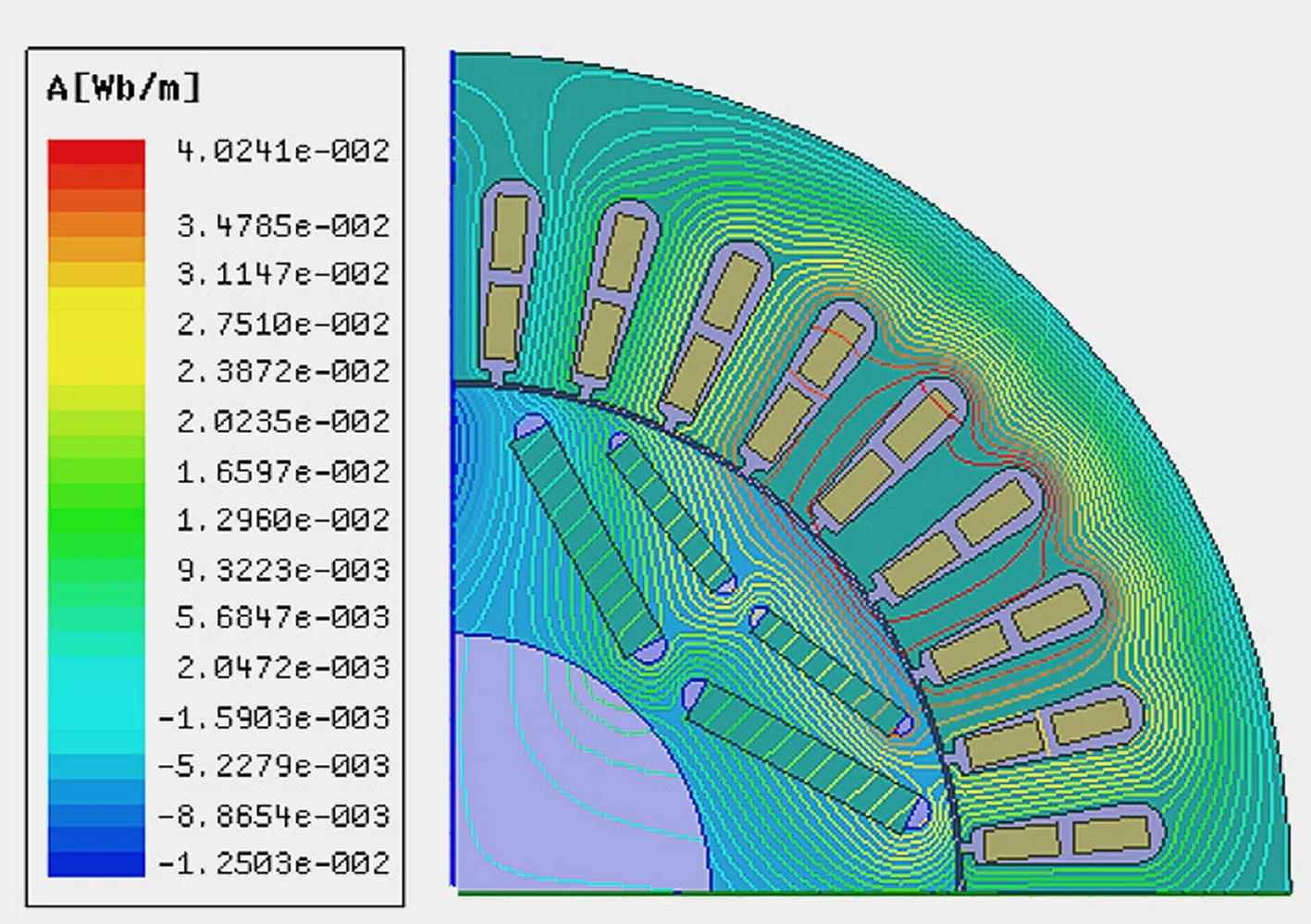
(h) 60%故障額定負載工況

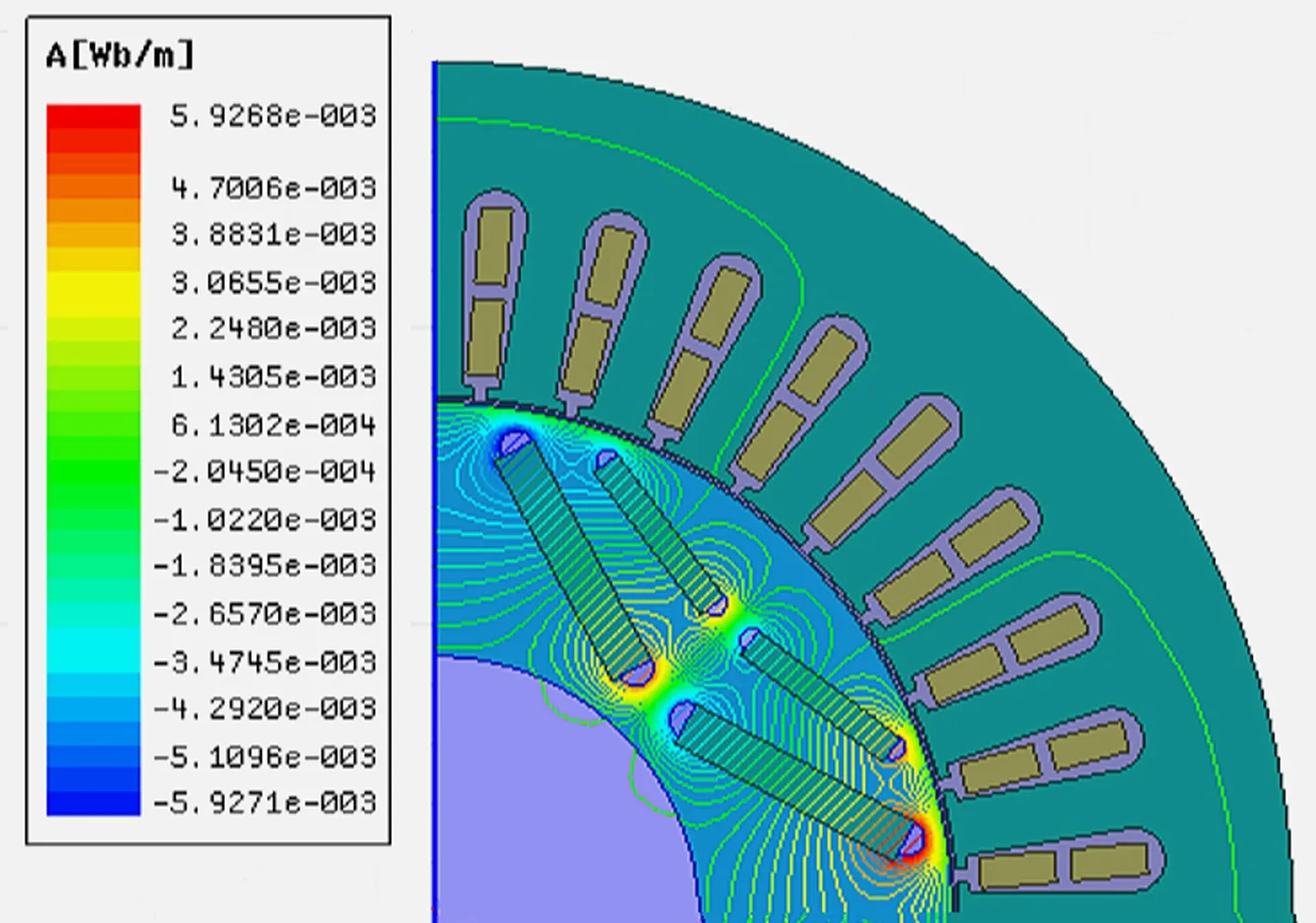
(i) 80%故障空載工況

(j) 80%故障額定負載工況

由圖2中空載和額定負載兩種不同工況對比可知，空載工況下，隨著故障程度的增加，磁感線變稀疏，數量明顯減少，數值也減小；額定負載工況下，磁感線數量看似變密集，實際上數值減小。因此，該耦合故障會引起電機電磁場的畸變，導致電磁場強度減小。

電機相關特征參數包括轉矩、相反電動勢、電流、轉速和轉子位置等，根據前面對永磁同步電機重要性能參數的計算分析以及該耦合故障的故障機理可知，轉矩和相反電動勢為典型特征參數，因而選擇對其曲線變化特點進行對比分析。

1) 轉矩曲線變化特點分析

不同工況下的轉矩變化曲線如圖3所示。為深入分析圖3(a)中曲線的變化特點，將其中一段時間內的曲線放大(見圖3(b))。由圖3可以看出，電機電磁轉矩的變化特點是，隨故障程度的增加，轉矩的幅值均減小；空載工況下的周期變化不明顯，額定負載工況下周期明顯變大。

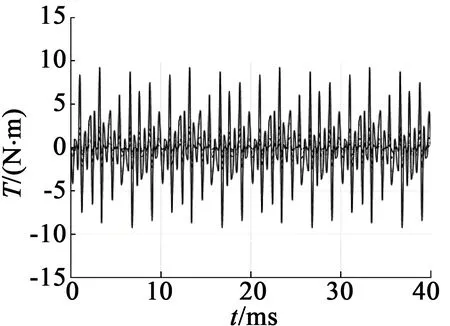
(a) 空載

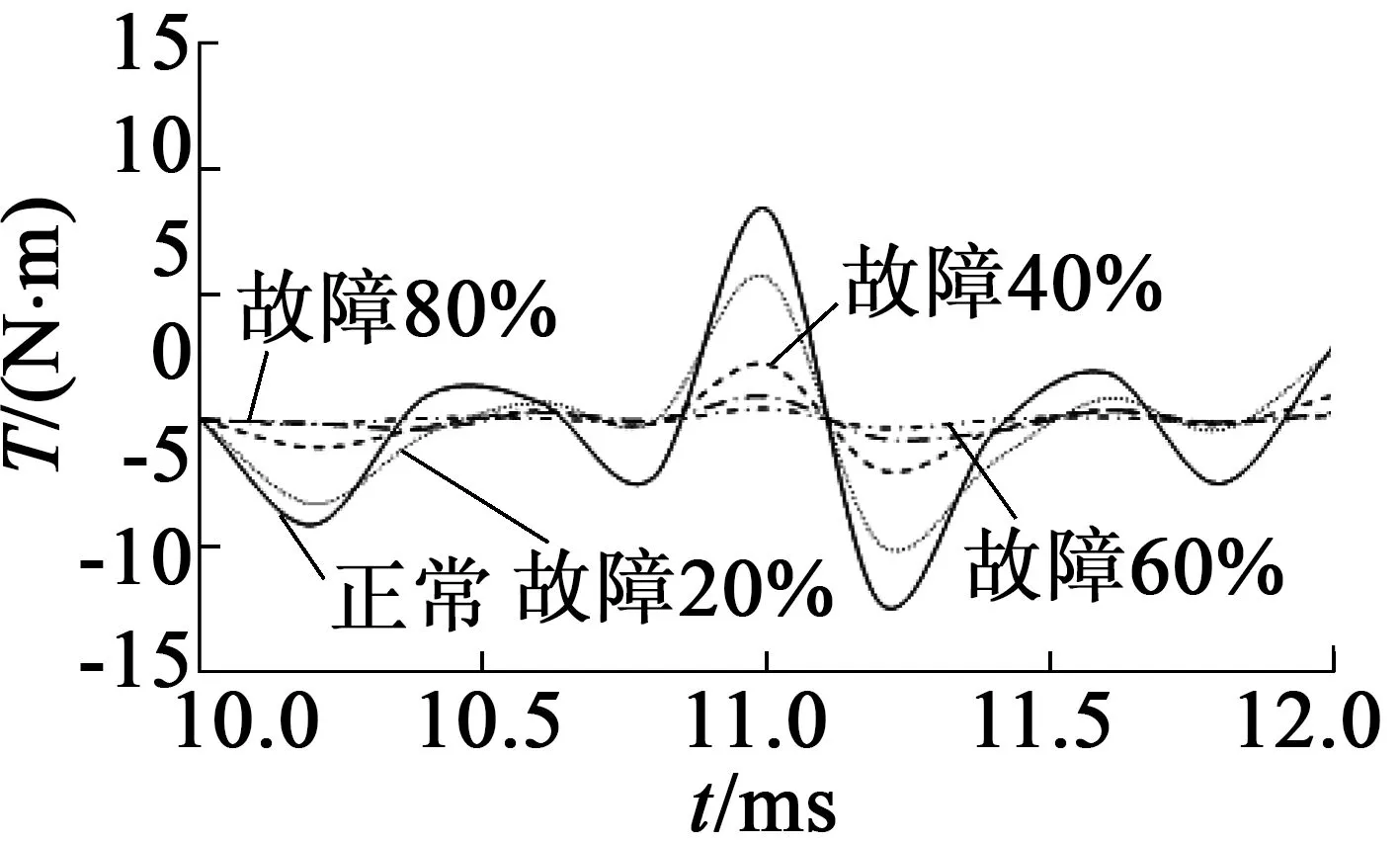
(b) 空載局部放大

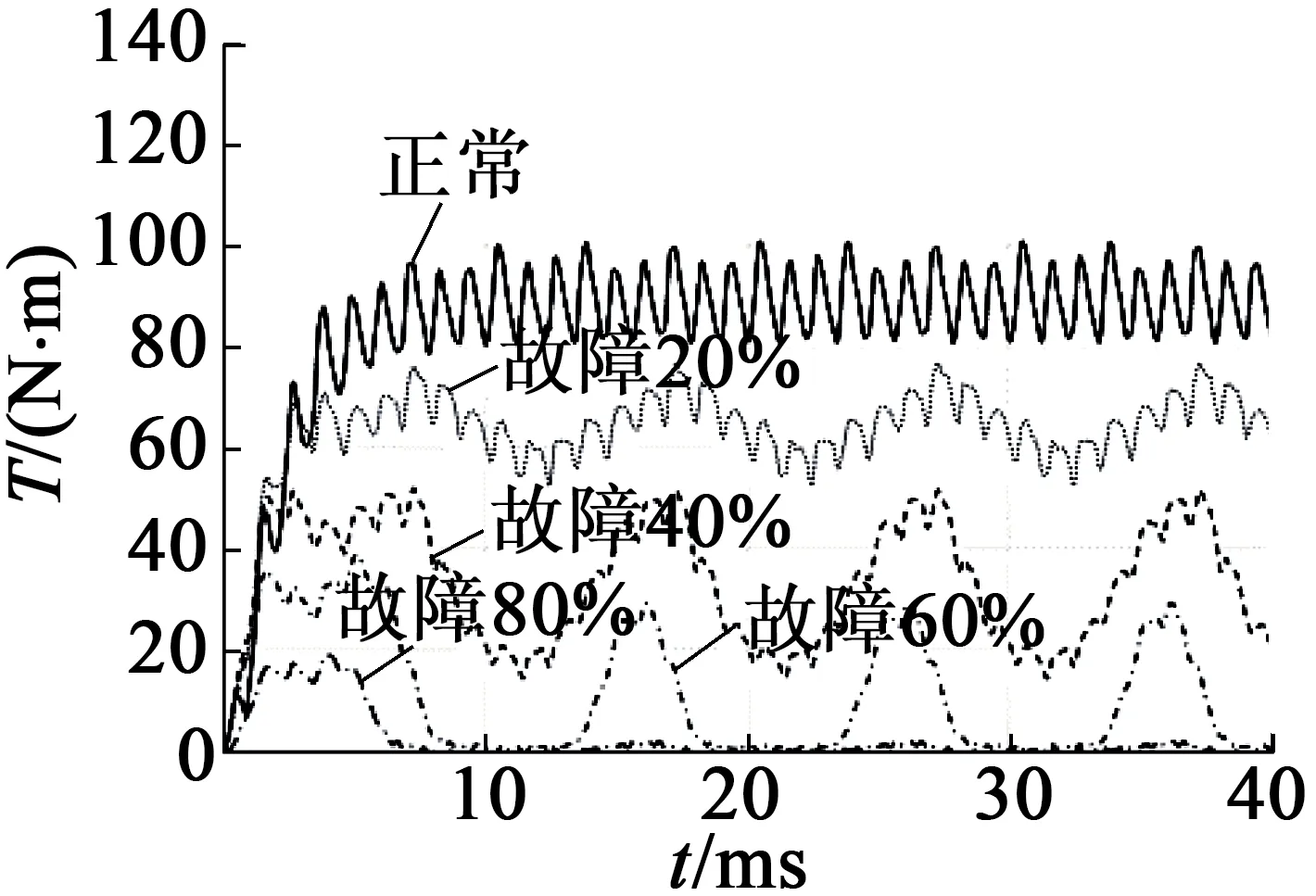
(c) 額定負載

圖3不同工況下轉矩曲線圖

2)相反電動勢曲線變化特點分析

如圖4所示，電機A相反電動勢的變化特點是，隨故障程度的增加，幅值均減小；空載工況下的周期變化不明顯，額定負載工況下周期有輕微變化。

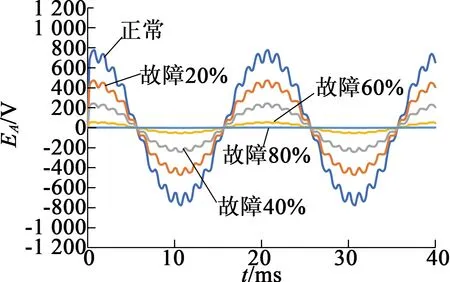
(a) 空載

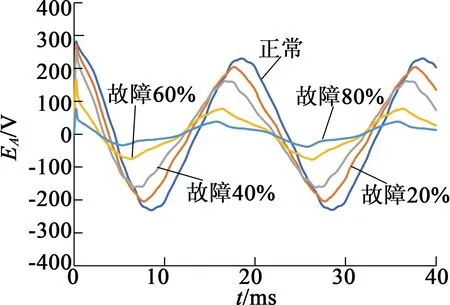
(b) 空載局部放大

圖4不同工況下A相反電動勢曲線圖

2.3 相反電動勢諧波含量分析

前面對電磁場分布和特征參數曲線的分析及仿真結果，僅給出了定性的變化趨勢。為進一步深入揭示永磁同步電機耦合故障的特性，利用傅里葉變換，分別分析不同工況以及不同故障程度下的相反電動勢諧波含量，如表2、表3所示(表中諧波含量是諧波與基波的比值，諧波次數是諧波頻率與基波頻率的比值，基波頻率是50 Hz)。

表2 空載工況下A相反電動勢諧波含量(單位：%)

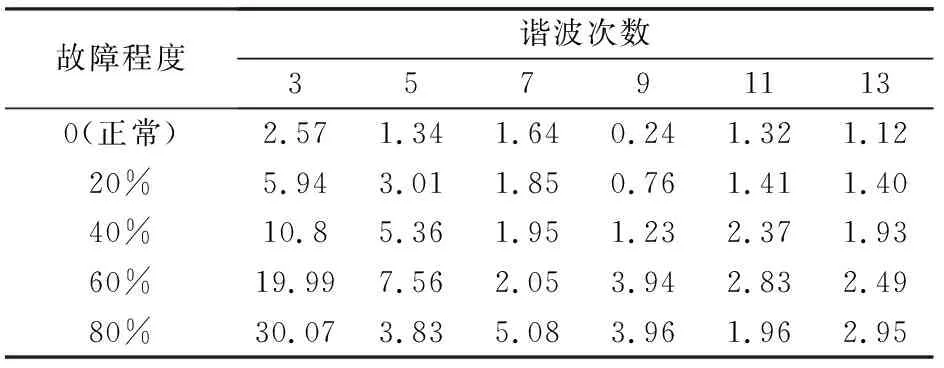
表3 額定負載工況下A相反電動勢諧波含量(單位：%)

由表2可知，空載工況下A相繞組反電動勢三次諧波含量呈小幅度增加趨勢，其它次數的諧波含量只有輕微改變，可忽略不計。

由表3可知，額定負載工況下A相繞組反電動勢三次諧波含量呈明顯增加趨勢，而其它次數的諧波含量雖有所增加，但相對于三次諧波來說可忽略。

綜合表2、表3可知，兩種不同工況下只有三次諧波含量變化最為明顯，其它次諧波含量較三次諧波含量而言，雖有變化但幅值較小，為此，特選擇三次諧波含量作為永磁同步電機匝間短路和永磁體退磁耦合故障的特征量，用以表征永磁同步電機是否存在對應耦合故障的判定依據。以此為基礎，額定工況下還可根據其增加量的大小進一步判斷電機的故障程度，如表4所示(表中的值為近似值，即在該數值左右即可)。

表4 三次諧波含量的增加量與故障程度的關系

3 數學模型驗證

3.1 永磁同步電機數學模型

永磁同步電機在三相坐標系下的數學模型[16]：

(22)

式中:ua,ub,uc分別為三相繞組電壓；ia,ib,ic分別為三相定子電流；Rs為定子繞組的電阻；φa,φb,φc分別為三相定子磁鏈；p為時間t的微分算子。

(23)

式中:

(24)

(25)

式中:LAA,LBB,LCC分別為定子繞組的自感；Mxx分別為定子繞組之間的互感；φf為永磁體交鏈于定子相繞組磁鏈的幅值；θ為轉角；L0S為主自感的恒定分量；L2S為主自感的倍頻分量。

3.2 數學模型解析

由仿真分析結果可將A相反電動勢作為判斷該耦合故障的特征量，因此通過數學模型求解驗證A相反電動勢的仿真曲線是否正確。

由于三相對稱，故三相電流大小相等，相位相差120°。將式(24)、式(25)代入式(23)可得:

將式(26)代入式(22)可得:

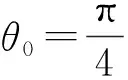
將式(18)代入式(27)得:

3.3 解析結果分析

由圖4可知，不同工況下的A相反電動勢曲線與正弦三角函數曲線(空載工況下的不平滑曲線是由于電機內部結構所致)非常相似，根據三角函數特性，式(28)可簡化成正弦函數曲線，這表明仿真得到的正常條件下的曲線趨勢和數學模型解析得到的曲線趨勢十分吻合。

將空載和負載工況下的φf分別代入式(28)中，可得到兩種不同工況下的A相電壓幅值分別為807.53 V和278.63 V。通過計算得到的幅值和仿真幅值相近。由于數學模型經過簡化，數值上有差距屬于正常范圍內。這表明前面建立的永磁同步電機二維物理模型是正確的，這為耦合故障仿真分析奠定了基礎。

4 結 語

耦合故障對永磁同步電機的電磁場分布和特征參數曲線都有明顯影響。電機出現耦合故障后電磁場強度減小，特征參數的幅值減小，周期也相應變化。

耦合故障對空載工況的電磁場分布影響明顯,隨著故障程度增加，空載工況下的磁感線數量減少明顯，且數值減小量也比額定負載多;耦合故障對額定負載的特征參數影響較大,隨著故障程度的增加，不同工況下各特征參數的幅值均減小，但額定負載工況下周期變化明顯。

三次諧波含量增加可作為判斷耦合故障的依據。在額定工況下，三次諧波含量的增加量可判斷電機的故障程度，即增加量越大，故障程度越重。