基于FSSI的環境激勵下機電振蕩特征參數快速識別方法研究*

王麗馨

(東北電力大學 電氣工程學院，吉林 吉林 132012)

0 引 言

隨著電力系統規模的不斷增大，低頻振蕩已成為制約大規模電能遠距離外送、威脅現代互聯電網安全穩定的關鍵問題之一。快速準確地獲取系統機電振蕩模式及模態信息對于大電網安全穩定運行具有重要意義[1]。

電力系統隨機響應數據以負荷投切等隨機擾動為激勵，數據量豐富，且蘊含大量系統實際工況的振蕩信息。隨著廣域測量系統在電力系統中迅速發展，以隨機響應數據為基礎的低頻振蕩分析法越來越受到學術界和工程界的廣泛關注[2-3]。文獻[4]利用頻域分解法從隨機響應信號中提取振蕩頻率、阻尼比和模態振型等信息。但對于阻尼良好的系統，該方法無法準確辨識系統阻尼比，同時對于頻率接近的模式區分存在困難。Zhou N[5]等人以隨機響應數據為基礎，利用改進的遞歸最小二乘法提取系統機電振蕩信息。但該方法數值穩定性較差。Khalilinia H[6]等人通過對獲得的隨機響應數據進行小波尺度分解從而得到系統模態信息。但小波函數及其參數的選擇對辨識結果影響較大。隨機子空間算法直接作用于時域數據，因而具有較好的頻率分辨率，同時在處理數據量較大以及動態過程較復雜的系統方面具有較好的適應性，成為基于量測信息參數辨識的常用方法[7-9]。但現有的隨機子空間算法大都需要對高維Hankel矩陣進行SVD分解，計算量大，同時計算過程相對復雜，計算耗時長，嚴重影響了SSI算法的在線應用。

為了進一步提高隨機子空間算法在電力系統機電振蕩參數識別方面的計算速率，本文提出了基于快速隨機子空間辨識法的電力系統機電振蕩參數識別方法。利用LQ分解取代了傳統隨機子空間算法中的SVD分解過程，在保證模態參數辨識精度的基礎上，極大提高了辨識速率。仿真算例表明本文所提方法在保證了辨識精度的同時極大提高了計算速度。

1 環境激勵下系統動態響應特征

系統實際運行過程中，負荷波動、新能源有功輸出的隨機性等均會給系統帶來隨機擾動。以負荷隨機波動為例，電力系統動態模型可以用如下的隨機微分代數方程形式描述[10]：

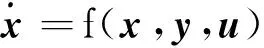
(1)

0=g(x,y,u)

(2)

式(1)為系統微分方程，描述了系統中發電機及相應的控制裝置、負荷等的動態過程，式(2)為系統的代數方程，一般由系統潮流方程及發電機、負荷等靜態方程組成。f和g為連續函數；x(x∈Rnx)為系統的狀態變量，如發電機功角等，y(y∈Rny)為系統的代數變量，如母線電壓，母線相角等，u為隨機波動變量。

假設負荷隨機波動服從(Ornstein-Uhlenbeck，OU)分布，建立負荷隨機波動的系統動態模型[11-12]：

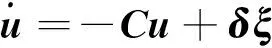
(3)

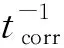
隨機擾動過程中，電力系統運行狀態未發生變化，即各臺發電機運行平衡點不變，則可以通過線性化系統狀態來近似分析系統狀態變量的動態過程。線性化式(1)～式(3)，同時消掉代數變量y，則：

(4)

式中fx、fy分別為式(1)中對應于x、y的雅可比矩陣；gx，gy，gu分別為式(2)中與變量x，y，u對應的雅可比矩陣。

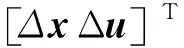
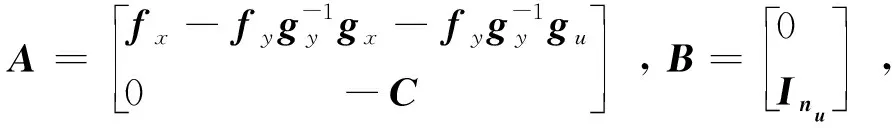
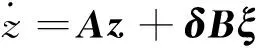
(5)

式(5)即為負荷隨機波動下，電力系統線性化狀態空間模型。求解得到系統n個振蕩模式對應的特征值λi=σi+jωi(i=1, 2, …,n)，則系統狀態變量的時域解析表達式為：

(6)

一般地負荷隨機波動幅值較小，加之系統中調速器等控制器的作用，使得系統狀態變量中的振蕩分量幅值亦非常小，使得測量得到的系統隨機響應信號外在表征為雜亂無章類似噪聲的信號。但通過對式(6)分析可知，表面看似雜亂無章的類似噪聲的隨機響應信號是環境激勵驅動下的系統動態響應和量測噪聲疊加的類噪聲信號，其中蘊含了豐富的電力系統動態信息，采用合適的技術手段可以從中提取系統的機電振蕩信息參數，及時掌握系統運行動態。

2 基于FSSI的機電振蕩特征參數識別

在實際應用中，量測數據在時間上都是離散的，經離散采樣后，可得如下隨機狀態空間系統[13]：

(7)

式中xk∈Rn為系統狀態量；yk∈Rl為測量得到的輸出量；wk∈Rn和vk∈Rl均為假定白噪聲，且E(wk)=E(vk)=0；A∈Rn×n和C∈Rl×n分別代表系統狀態矩陣和輸出矩陣；Δt為采樣間隔。

對式(7)所示的隨機系統，由采樣時序數據組成Hankel矩陣：

(8)

式中Yp表示過去時刻數據，Yf為將來時刻數據；H∈R2li×j，i為塊矩陣行數，且要大于系統階數2n；j為Hankel矩陣列數；若l為系統測點個數，則Hankel矩陣共有2li行；若量測數據樣本采樣點數為r，為了保證所有數據均能被放入Hankel矩陣中，必須滿足關系式j=r-2i+1。

高維Hankel矩陣的分解是影響隨機子空間辨識方法計算速率的關鍵因素，傳統隨機子空間利用SVD分解來處理Hankel矩陣，計算效率較低，影響了隨機子空間算法的計算速度。本文引入LQ分解代替SVD分解，有效的提高了計算效率。

將Yf投影到Yp得到正交投影矩陣，即：

Yf/Yp≡YfYp(YpYp)?Yp=Oi

(9)

式中，Oi正交投影矩陣，?表示相應矩陣的偽逆。

利用正交投影計算得到延伸觀測矩陣，即：

(10)

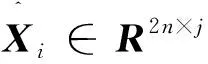
以Hankel矩陣LQ分解來代替式(8)投影計算：

lilij

(11)

(12)

由式(12)可知，L21與Γi列空間是同構的，因此在求得Hankel矩陣LQ分解的下三角矩陣L21后，即可計算出延伸觀測矩陣Γi。

進而計算L21奇異值(SVD)分解：

(13)

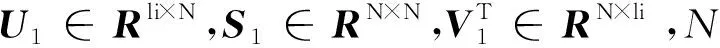
延伸觀測矩陣Γi可由矩陣U的前N列確定：

Γi=U1

(14)

計算求得連續系統狀態矩陣Ac及輸出矩陣Cc：

(15)

(16)

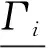
輸出矩陣Cc為延伸觀測矩陣Γi的第1行，即：

Cc=Γi(1,:)

(17)

連續系統狀態矩陣Ac確定之后，對其進行特征值分解：

Ac=ψΛψ-1

(18)

式中Λ=diag(λk)∈Rn×n，k=1,2,…,n；λk為第k階模態特征值；ψ為系統特征向量。

特征值與振蕩頻率和阻尼比存在下列關系：

(19)

式中：λk為系統第k個特征值；ωk為第k個振蕩模式的振蕩頻率；ζk為第k個振蕩模式的阻尼比。

進而求得系統第k個振蕩模式的振蕩頻率及阻尼比[14]：

(20)

式中ak=Re(λk),bk=lm(λk)

系統的模態振型定義為輸出點處的系統特征向量：

φ=Ccψ

(21)

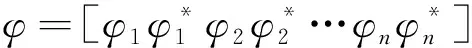
利用快速隨機子空間算法辨識系統機電振蕩模態參數，及時掌握系統當前的運行動態，對于調度運行人員進行準確有效的電力系統小干擾穩定分析具有重要意義。

3 仿真分析

3.1 4機2區域系統計算與分析

本節以IEEE 4機2區域系統為例，對提出的基于FSSI算法的電力系統模態參數快速識別方法進行仿真分析。IEEE 4機2區域系統結構如圖1所示，數據參見文獻[15]。

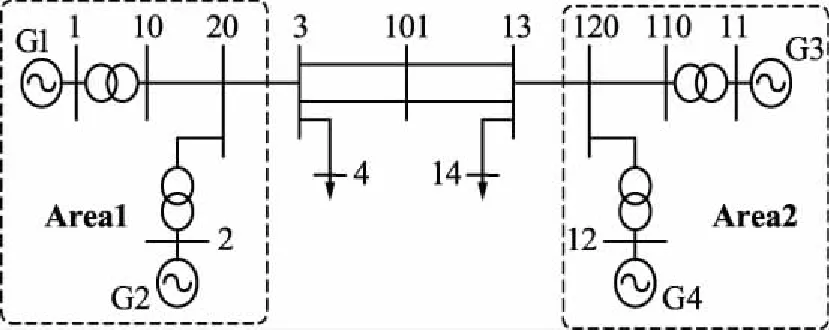
圖1 4機2區域系統接線

利用小干擾穩定分析算法(Small Signal Analysis Stability, SSAT)計算系統基礎運行方式下的機電振蕩模式，分析結果如表1所示。三個機電振蕩模式對應的模態振型如圖2所示。

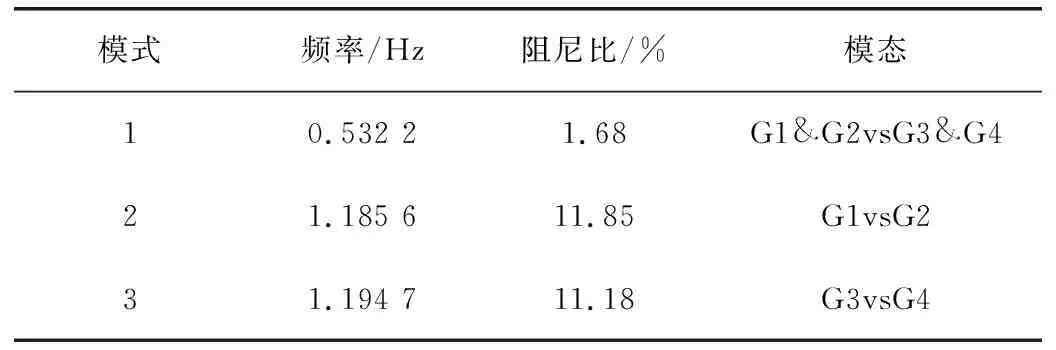
表1 4機2區域系統特征值分析結果

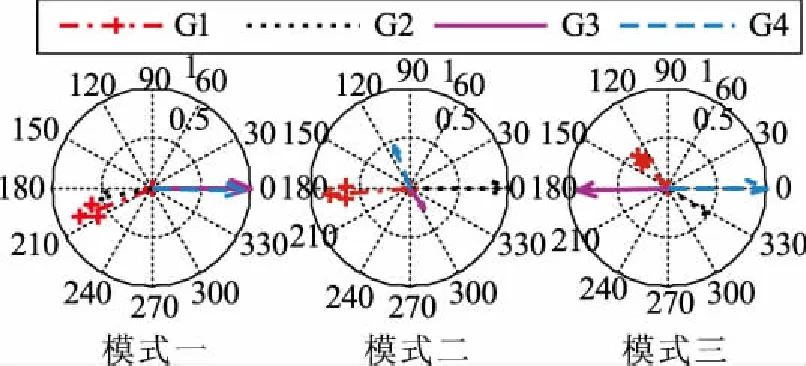
圖2 4機2區域系統模態振型圖

為了驗證本文所提方法在電力系統模態參數識別方面的準確性和有效性，為模擬實際系統的負荷隨機波動，本文假設節點4和節點14處的負荷以基礎運行值的5%隨機波動。

以系統各臺發電機的角頻率隨機響應數據為基礎，在惠普Z820(CPU：2*Intel至強E5-2600v3，2.6 GHz；內存：32 GB)工作站上分別利用傳統隨機子空間算法和本文提出的快速隨機子空間算法，針對不同長度時間段的隨機響應數據辨識系統模態參數。各長度數據段的CPU計算時間如表2所示。以120 s長度的發電機角頻率隨機響應數據段為例，分別利用傳統SSI算法和本文提出的FSSI算法辨識系統模態機電振蕩模態參數，分析結果如表3所示。

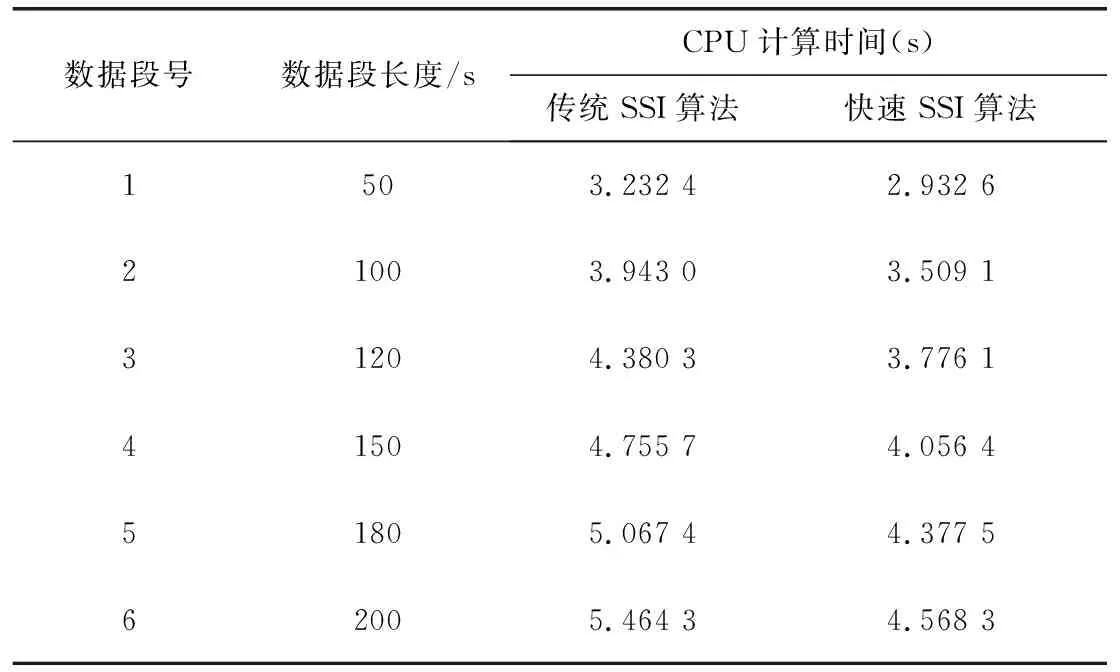
表2 4機2區域系統CPU計算時間

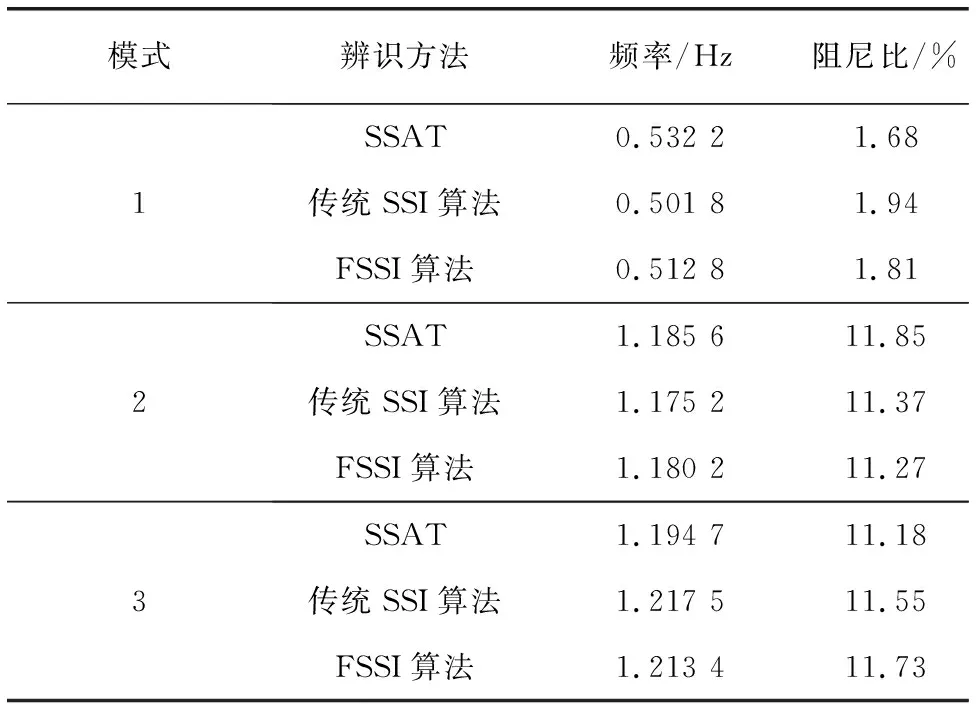
表3 4機2區域系統模態參數辨識結果

結合表2、表3及圖3分析可知，利用本文提出的FSSI算法能夠準確辨識出系統3個機電振蕩模式，相對于傳統SSI算法，辨識得到的三種模式振蕩頻率及阻尼比結果與基礎運行方式的機電振蕩參數更加接近；在計算速度方面，對于相同長度數據段，若數據較短，兩種方法的計算時間相差不明顯，但對于樣本數據較多的情況，本文提出的方法具有較大的優勢，CPU計算時間更少，具有更快的計算速率，能夠更好的滿足現代電力系統對安全穩定評估快速性的要求。

以系統角頻率隨機響應數據為基礎，利用本文提出的快速隨機子空間算法辨識得到系統振蕩頻率、阻尼比及模態振型信息。選取時長為20min隨機響應數據為基礎，以10s為數據窗口，每6s滑動一次計算窗口數據，20min內計算統計結果如表4所示，三個機電振蕩模式的頻率-阻尼比關系如圖4所示。

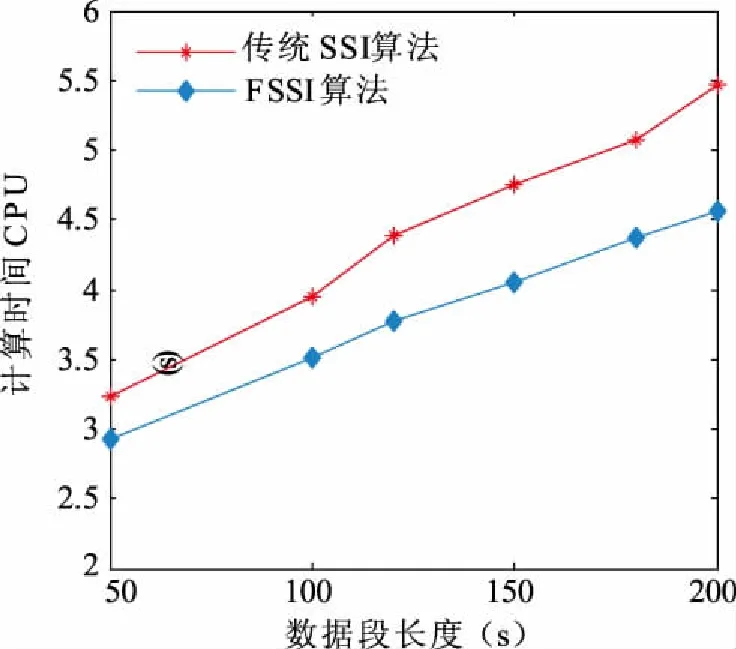
圖3 4機2區域系統CPU計算時間變化圖

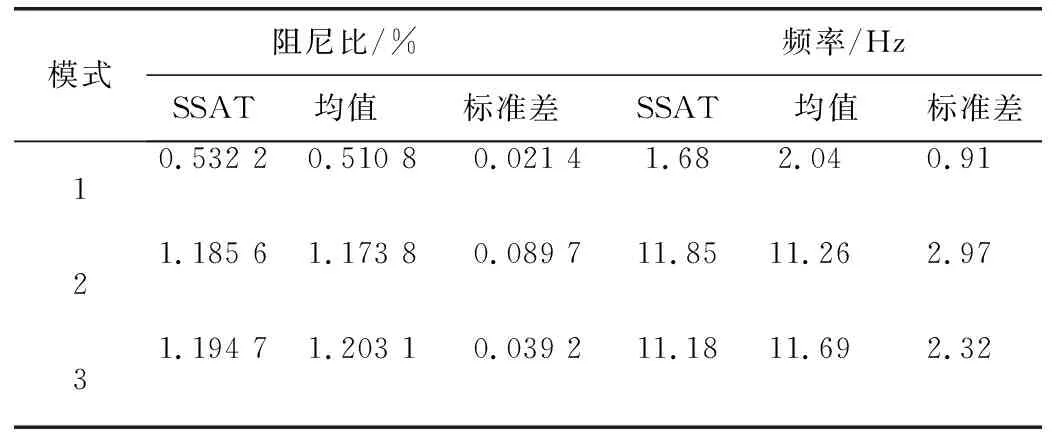
表4 機電振蕩參數辨識結果

結合表1和表4分析可知，利用本文提出的FSSI算法辨識得到系統3個機電振蕩模式的振蕩頻率分別為：0.520 8 Hz、1.173 8 Hz、0.532 2 Hz、1.203 1 Hz，基礎運行方式下振蕩頻率分別為：0.532 2 Hz、1.185 6 Hz、1.194 7 Hz，統計均值與基礎運行方式值十分接近，且標準差很小；同樣，辨識得到的阻尼比分別為1.87%、11.26%、11.69%與基礎運行方式值1.68%、11.85%、11.18%接近，標準差小。

快速隨機子空間20 min內辨識得到的頻率-阻尼比關系如圖4所示。分析圖4可知，系統各振蕩模式每次滑動窗內辨識得到的頻率和阻尼比均以基礎運行值為中心分布，辨識得到的結果與基礎運行值接近，辨識結果良好。

同時，圖5所示的基于角頻率隨機響應數據辨識得到的模態振型反映的機組參與振蕩的信息與圖2所示的基礎運行方式的模態振型形基本一致，進一步驗證了本文提出的快速隨機子空間方法的有效性。

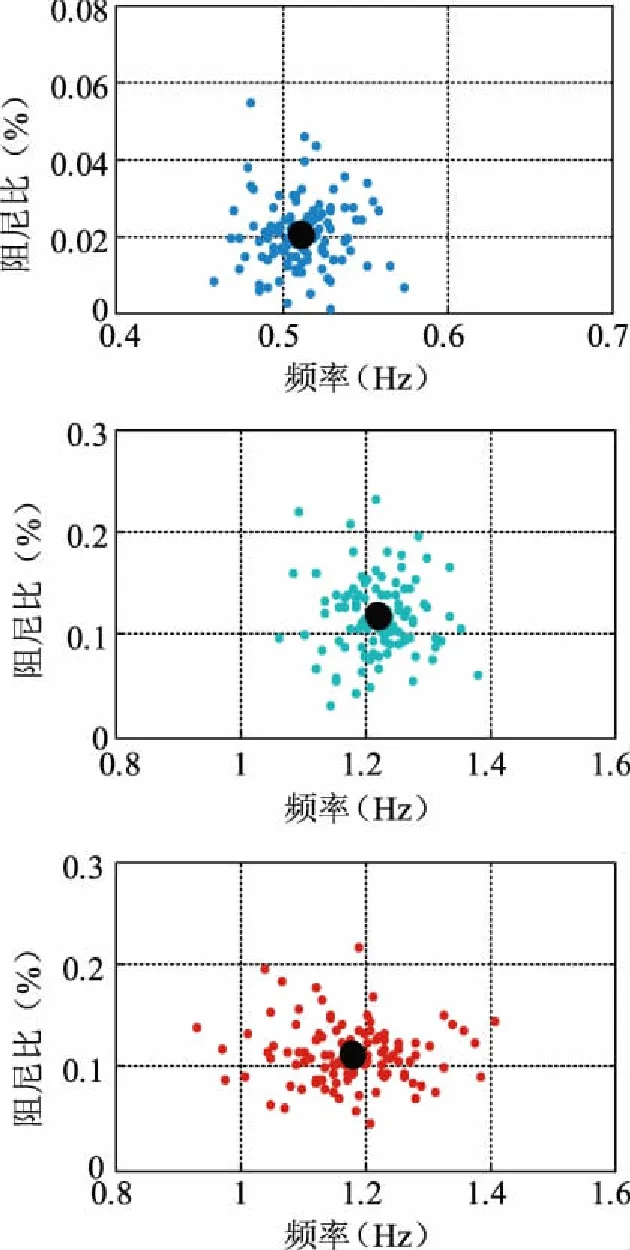
圖4 4機2區域頻率-阻尼比辨識結果

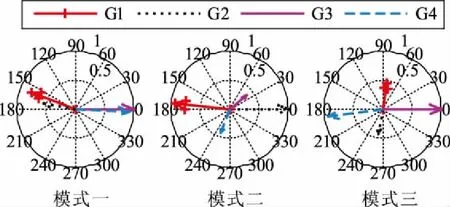
圖5 4機2區域系統模態辨識結果

3.2 IEEE 16機68節點系統

IEEE 16機68節點系統結構圖及數據參見文獻[16]。

同樣，對系統進行小干擾穩定分析，獲取基礎運行方式下系統機電振蕩模式。就實際系統而言，區間振蕩影響更為廣泛，是調度運行人員主要關心的振蕩模式。因此，本文主要針對16機68節點系統的區間振蕩模式進行分析，得到系統4個區間振蕩模式參數如表5所示，模態振型如圖6所示。

與IEEE 4機2區域系統分析類似，假設系統內所有負荷均以基礎運行值的5%隨機波動，分別利用傳統SSI算法和本文提出的FSSI算法，以角頻率隨機響應數據為基礎辨識系統模態參數。不同長度數據段的CPU計算時間如表6所示。

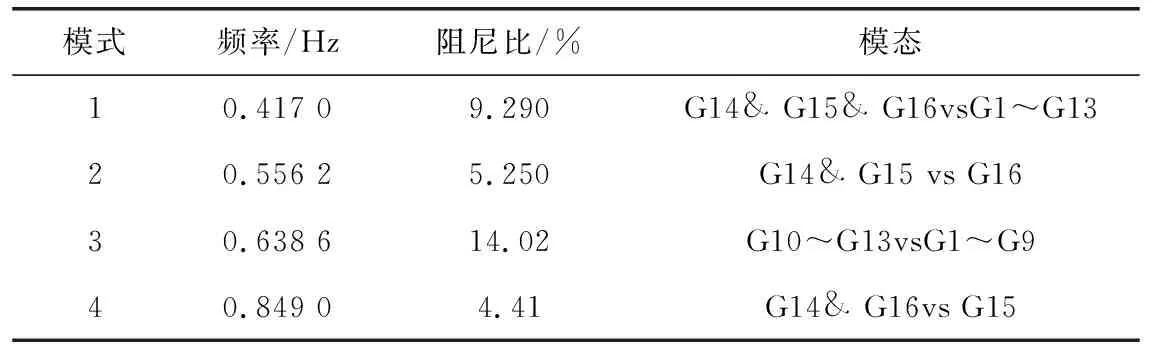
表5 16機68節點系統特征值分析結果

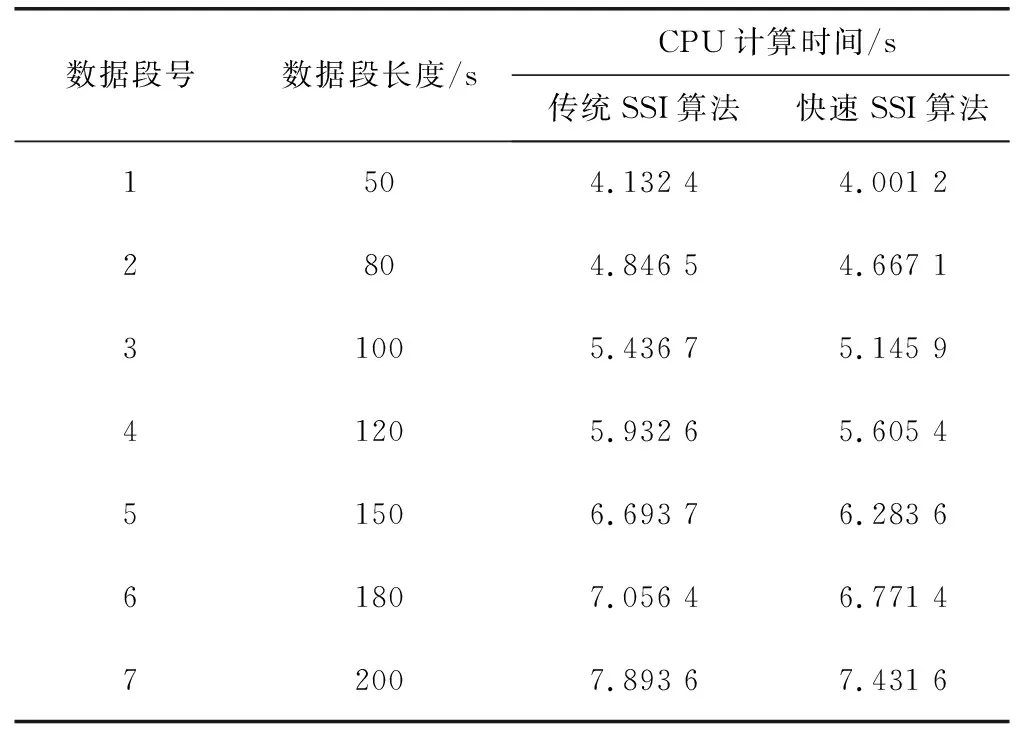
表6 16機68節點系統CPU計算時間

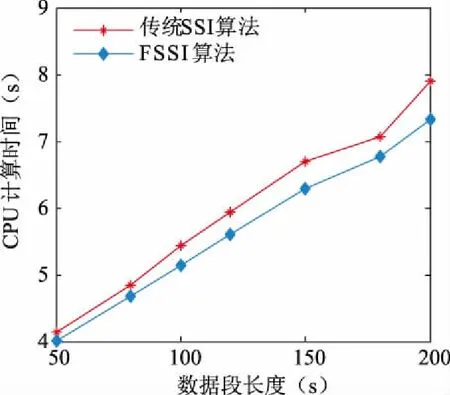
圖7 16機68節點系統CPU計算時間變化圖

結合表6和圖7分析可知，由于16機68節點系統相對于4機2區域系統的系統規模大，兩種辨識算法所需的時間均有所增加，但本文提出的快速隨機子空間法相對于傳統的隨機子空間法的計算時間要少，計算速度快。

以20 min角頻率隨機響應數據為基礎，10 s為數據窗口，6s滑動一次窗口數據，16機68節點系統20 min辨識得到的統計結果如表7所示，頻率-阻尼比關系如圖8所示。

分析表7可知，快速SSI辨識得到的4個區間振蕩的振蕩頻率和阻尼比與基礎運行方式下的模態參數十分接近，同時結合圖8亦可以看出，每次滑動窗內辨識得到的頻率和阻尼比以基礎運行值為中心，在其周圍分布，進一步驗證了本文所提方法在系統模態參數辨識方面的有效性和準確性。

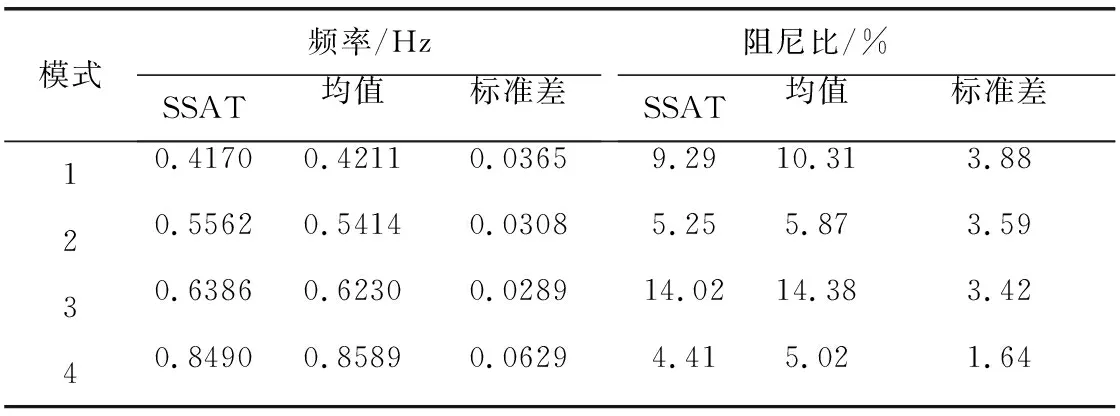
表7 16機68節點系統辨識結果統計

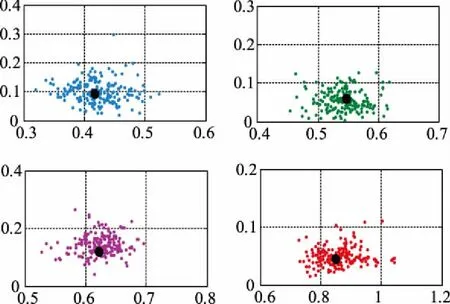
圖8 16機68節點系統頻率-阻尼比辨識結果

4 結束語

本文推導了環境激勵下電力系統動態響應的解析表達式，利用快速隨機子空間算法辨識系統振蕩頻率、阻尼比及模態振型，仿真分析與計算表明：

(1)環境激勵作用下的系統隨機響應蘊含豐富的動態信息，采用合適的參數識別技術能夠從中提取出系統機電振蕩參數；

(2)與傳統隨機子空間相比，本文提出的快速隨機子空間算法以LQ分解法為基礎，降低了CPU計算時間，有效提高了辨識速度，更好的滿足了電力系統安全穩定評估快速性的要求；

(3)快速辨識系統機電振蕩參數，及時掌握系統動態信息，為調度運行人員采取及時有效的控制措施提供依據。

電力系統模態參數識別的結果是為了更好的實現電力系統小干擾穩定分析控制，如何根據辨識結果采取有針對性的控制措施是下一步需要考慮的問題。