微動條件下材料磨損率的一種計算分析方法?

楊曉麗 王斌容 胡海云

(北京理工大學物理學院,北京 100081)

1 引 言

微動一般是在機械振動、疲勞載荷、電磁振動或熱循環等交變載荷作用下,接觸表面間發生的振幅在微米量級的相對運動.在結構工程中如各種連接件、各種緊固和夾持機構、各種彈性支撐機構、振動環境下的零部件等廣泛存在微動現象.微動可以直接導致表面磨損,造成零件松動、功率損失或噪音增加,也可能由于磨屑聚集造成運動副咬死,有時也會引起災難性事故.所以對微動磨損的研究具有現實意義,也越來越受到國內外學者的廣泛重視[1].

磨損直接表現為物體表面材料的損失,因此,磨損過程中材料磨損率的研究對微動磨損的分析具有重要的意義.郝宏偉等[2]對高氮不銹軸承鋼進行了不同應力和不同滑動速度下的微動磨損試驗,得出試驗鋼的摩擦因數隨應力和滑動速度的增加而減小;磨損率隨應力和滑動速度的增加而增加.王璋等[3]對純鐵開展了球/平面接觸模式下的沖擊微動磨損試驗,在增大沖擊能量的條件下,磨損體積、磨損率也隨之提高.丁燕等[4]對鈦合金TC4-DT在不同試驗條件下的抗微動性能進行了研究,并以磨損量、摩擦因數為指標分析了其微動摩擦磨損特性.張德坤等[5]對6×19點接觸式礦用提升鋼絲繩進行了鋼絲的微動磨損試驗研究,以摩擦系數和磨損深度作為評定微動磨損的參數,分析了不同載荷下摩擦系數的變化規律以及載荷、循環次數的變化對鋼絲試樣磨損深度的影響.以上研究都是通過對具體材料進行磨損試驗來分析磨損率,缺乏統一的、普適的理論對材料磨損率進行計算分析.

2017年第21屆材料磨損國際會議[6]指出摩擦學建模方面的工作具有巨大的理論指導意義,是未來大力發展的課題.微動磨損過程中摩擦、黏著和磨損三者密切相關,均需了解發生在分子水平的非平衡過程決定的宏觀行為.非平衡統計理論正是從微觀機理出發,通過統計方法推導出宏觀特性及演化規律的理論方法,而微動摩擦學系統的不可逆性、時變性和隨機性正好符合非平衡理論模型建立的依據.本文借助不對稱雙勢阱模型,利用非平衡統計理論提出了一種新的研究微動磨損過程中磨損率的計算方法,并進一步對磨損過程中磨損時間、材料的勢阱寬度及載荷正壓力對磨損率的影響進行了分析.

2 理論模型

2.1 不對稱雙勢阱模型

將發生微動磨損的兩種材料A和B的近表面部分看作一個摩擦副系統.其中,設材料A為軟材料,材料B為硬材料.磨損表現為材料表面物質的損失,摩擦表現為阻礙相對運動的作用力及其產生的機械能損耗.也就是說,磨損影響系統的結構,摩擦影響系統的功能.本文重點研究的是微動摩損過程中磨損量的變化情況,因此,研究側重于摩擦副表層材料的損失.

借鑒分子動力學[7,8]的基本思路,從納米量級考慮粒子在摩擦副系統中的運動.因摩擦副系統中兩接觸材料的不同是微滑產生的條件(若組成摩擦副的材料相同,根據Hertz理論力學[9]分析,兩接觸體所產生的切向位移相同,則相對滑動就不可能發生),在界面處兩不同材料能量發生了變化,因此可以假設兩接觸材料中的粒子處在不同的兩個勢阱中[10].

圖1所示不對稱雙勢阱模型的勢能函數表達式為

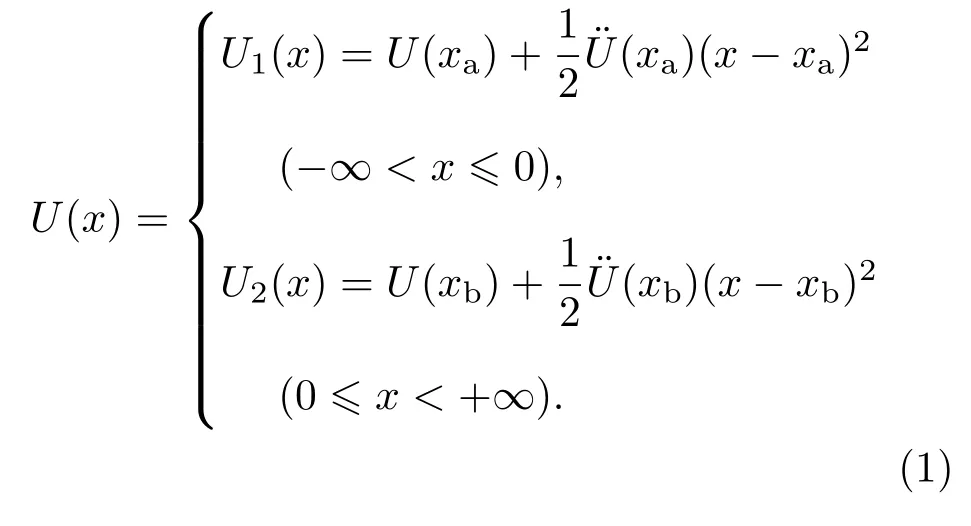
當x=0時,U1(x)=U2(x);其中U(x)為摩擦副系統中材料的勢能函數,U1(x)和U2(x)分別為兩材料A,B的粒子處在各自勢阱中的勢能函數;x為兩材料中粒子所在位置到材料表面的距離,x=0為兩材料的接觸表面,x=xa和x=xb分別表示兩材料A,B的勢阱底部;U(xa)和U(xb)分別為距兩材料接觸表面xa和xb位置粒子的勢能;和分別與A,B兩勢阱的寬度有關.

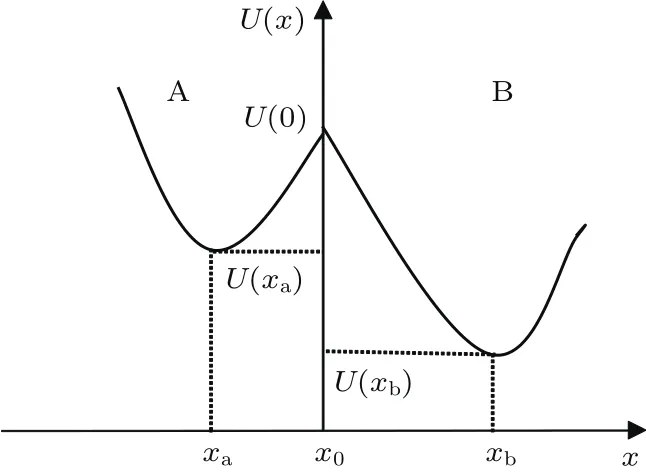
圖1 不對稱雙勢阱模型Fig.1.Asymmetric double well model.

不對稱雙勢阱模型中決定兩勢阱形狀的量,如勢阱底部最小值、勢壘高度和寬度等由兩材料A,B本身的性質決定,而在實際微動過程中,粒子在兩勢阱中的運動及轉移受到兩材料間的接觸時間、法向載荷、滑移距等的影響.因此,兩摩擦副間的磨損過程就可以看作態A(材料A)和態B(材料B)間粒子的轉移.在無外界環境影響時,初態處于原勢阱的粒子仍處在原勢阱中,它們各自在本勢阱中趨于定態.但在實際生活中,摩擦副系統所處的環境總會有漲落或勢壘壁熱能產生,這種環境引起不可避免的噪聲使摩擦副系統處于振動狀態,兩摩擦副材料表面產生微滑,導致磨損,即微動磨損.在雙穩態勢中,振動引起系統中的粒子在亞穩態和穩態間轉移,這個過程就是粒子在兩個勢阱間進行交換,使系統從局域平衡過渡到整體平衡的過程.

2.2 非平衡統計理論模型

統計力學方法[11]的起點是系統的微觀結構和粒子間的相互作用,即系統的微觀模型.一旦微觀模型確定之后,原則上可以采用力學的方法分析出系統所處的微觀狀態.通過分析這些微觀狀態和宏觀狀態之間的對應關系,并引入適當的假設,求解方程,可得到表征系統特性的關鍵,即分布函數.由此可討論系統的宏觀平均特性,從而導出宏觀量.

微動摩擦學系統是典型的開放的動態非線性復雜系統,具有很強的系統依賴性、時變性、隨機性和不可逆性,系統的各組元間相互作用,微觀結構的微小變化可引起宏觀量的改變,這些性質正是使用非平衡統計理論的依據.因此可以從微動摩擦學系統的微觀機理出發,基于非平衡統計理論,研究系統狀態的變化規律.

當受到外界環境影響,使兩材料的摩擦副系統處于振動狀態下時,材料內部的粒子會不斷運動.由于材料的相結構、缺陷及范性變形等的不均勻性,其微觀結構可看成是平均結構背景上疊加了這種不均勻的漲落.平均結構是確定的,不均勻性漲落是隨機的.粒子在運動過程的各階段,因這種不均勻性漲落的隨機存在,使其速率與所經途徑有關且一直在隨機變化.所以,可以將粒子的運動看成隨機過程.描述這個過程的方程是一個隨機微分方程,具體如下.

設t表示在振動作用下粒子在材料內的運動時間,x(t)表示t時刻粒子運動的位移,表示t時刻粒子的運動速率.由于摩擦副系統中的材料可看成是確定性背景結構上疊加了隨機性漲落,故粒子的運動速率遵守以下廣義Langevin方

程[12]:

其中k(x)為粒子運動速率的確定部分,即平均運動速率;f(x,t)為粒子運動速率的隨機部分,即漲落運動速率.在一定外界振動條件下,k(x)由平均結構和外界振動共同決定;f(x,t)由不均勻性漲落決定.

由于粒子的運動只與當時及稍早的外界振動和材料微觀結構有關,而與其更早的歷史無關,故可將其運動過程看成一個馬爾可夫過程.依據隨機理論[13],低速率運動的粒子f(x,t)為乘性噪聲,可表示為

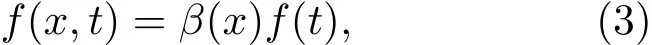
式中β(x)為乘性因子;f(t)為白噪聲,且f(t)是高斯分布,滿足條件

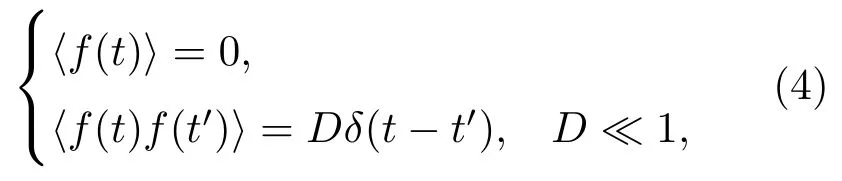
其中D為擴散系數.則(2)式變為

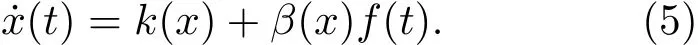
描述一個隨時間演化的動力學系統通常用兩種等價的方程:一種是動力學變量隨時間演化的方程,即廣義Langevin方程;另一種是概率密度函數隨時間演化的方程,即Fokker-Plank方程.廣義Langevin方程描述單個粒子轉移,為了建立大量粒子的系統,可以得出相應的Fokker-Plank方程,從而推出勢阱內粒子的概率密度分布情況.

根據隨機理論,與Langevin方程對應的Fokker-Plank方程[14]為

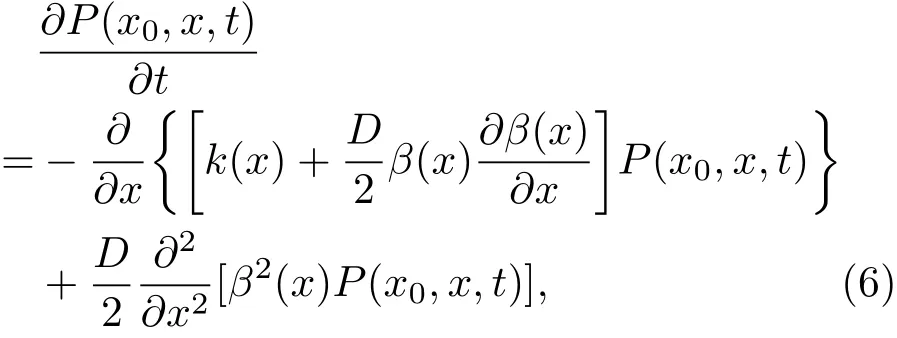
其中P(x0,x,t)dx表示在振動環境下,初始距材料表面x0處位置的粒子在t時運動到距表面x和x+dx間位置的概率,P(x0,x,t)稱為概率密度分布函數.

根據外界環境漲落和材料結構背景漲落的特性,對于(5)式中k(x),β(x)和(6)式中的D有如下關系:

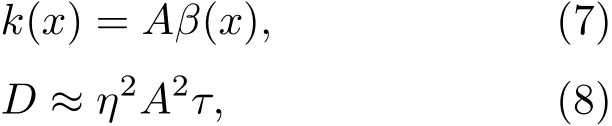
其中τ為微動磨損的平均時間,η為總的相對偏差,A為與x無關的常量.則Foker-Planck方程(6)變為

3 計算結果與討論

3.1 模型應用

對于穩態系統,在微動的初始階段,黏著材料可能轉移到對磨面上,也可能轉移回來.對于不同材料配副,由于硬材料B的表面比較不易破壞,磨損主要發生在軟材料A上,粒子從低強度低硬度表面轉移到高強度高硬度表面.因此,我們以軟材料A中的粒子為研究對象,粒子受到黏滯阻力、勢阱力和隨機力的作用.

初始時刻粒子處于勢阱A中,其運動方程為

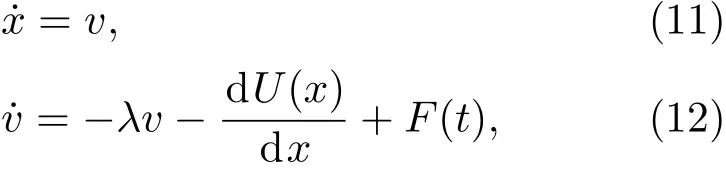
其中x為材料中粒子所在位置到材料表面的距離,v為粒子運動的速度,λ為耗散系數,?λv為黏滯阻力,U(x)為勢能函數,為勢阱力,F(t)為漲落力.

微動磨損過程中,摩擦副系統內兩材料間相對位移很小,類似于高黏度情況,所以可近似認為與(12)式聯立可得

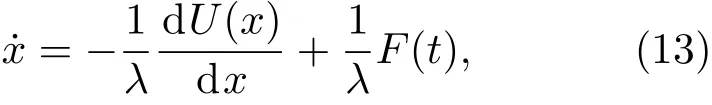
此處,為方便計算,可設黏滯系數λ=1,則(13)式變為

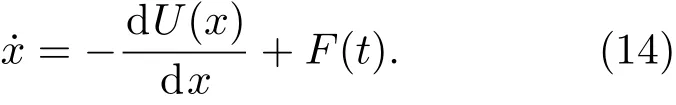
由不對稱雙勢阱模型的函數(1)式知,材料A中粒子在勢阱A中的勢能函數為

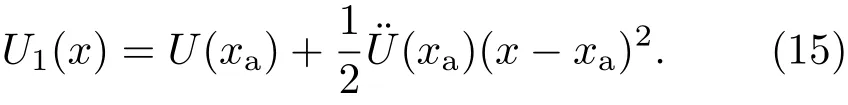
將(15)式代入(14)式得粒子在勢阱A中運動的Langevin方程為

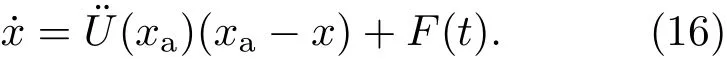
由(5),(7)和(16)式可得

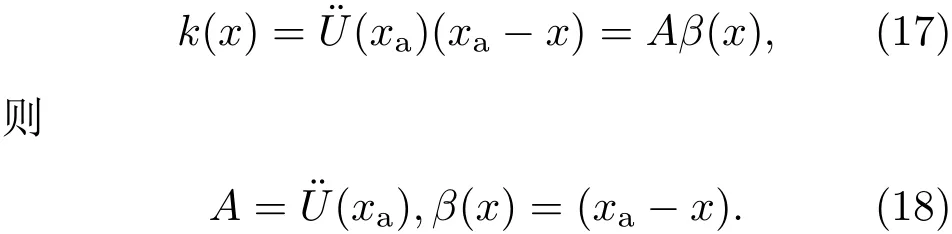
根據(8),(10)和(18)式,對于材料A內在勢阱A中運動的粒子,其概率密度分布函數為

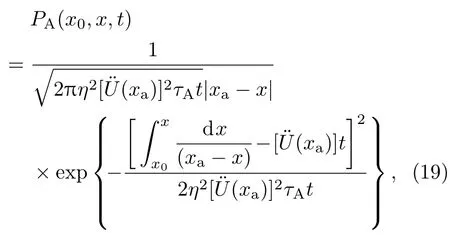
其中τA為粒子在勢阱A中運動的平均時間.

同理分析可得,對于材料B內在勢阱B中運動的粒子,在振動環境下,粒子的概率密度分布函數為

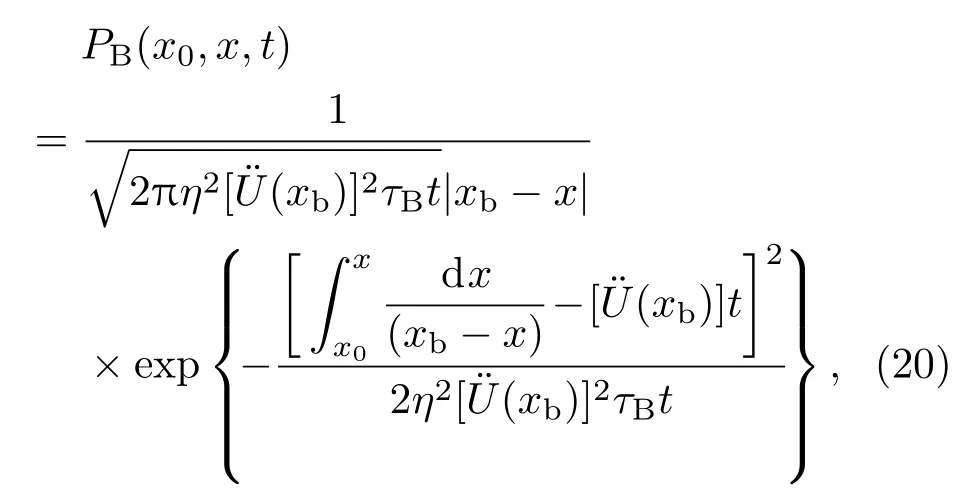
其中τB為材料B內粒子在勢阱B中運動的平均時間.

3.2 計算與結果分析

將模型應用于由金屬材料Mg(材料A)和Fe(材料B)組成的摩擦副系統.由于微動磨損主要發生在兩接觸材料的近表面部分,因此僅研究距材料表面微米量級位置的粒子在勢阱中的運動.故在雙勢阱模型表達式(1)中,取兩材料接觸表面x0=0 m,表面勢能U(x0)≈2×10?19J,兩材料A,B勢阱底部位置的值分別為xa=?2×10?6m,xb=2×10?6m. 根據文獻[16]中數據可得材料A(Mg)和B(Fe)的勢阱底部勢能分別為U(xa)≈?1×10?19J,U(xb)≈?3×10?19J.計算可得:10?7J/m2.

在整個微動磨損過程中,粒子運動的平均時間τ滿足

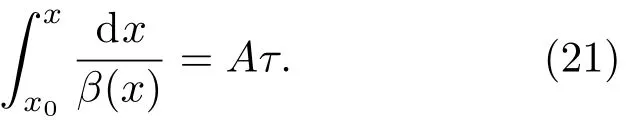
將(18)式代入(21)式,并代入數據可解得粒子在勢阱A中運動的平均時間τA=2×107s.同理,可計算出粒子在勢阱B中運動的平均時間τB=1.2×107s.

(6)式中P(x0,x,t)表示粒子從初始位置距材料表面x0處位置在t時運動到距材料表面x處位置的概率密度分布函數.因我們要研究的是微動磨損過程中材料的磨損,即粒子從材料內部到達材料表面的情況,所以可以用x表示材料表面,其值為0.將x0看作變量,其變化范圍為要研究的勢阱底部到表面部分,這里取為(?2×10?5,0]m和(0,2×10?5]m.

將上述數據分別代入(19)和(20)式并繪圖,可得到不同情況下材料內各處粒子的概率密度分布情況.圖2和圖3分別為在勢能函數不變的情況下,不同時刻摩擦副系統內兩材料A,B中距材料表面不同位置的粒子可到達材料表面的概率密度分布;圖4和圖5分別為在時間不變的情況下,對于摩擦副系統中兩材料A,B在不同勢阱寬度下,各位置的粒子可到達材料表面的概率密度分布.

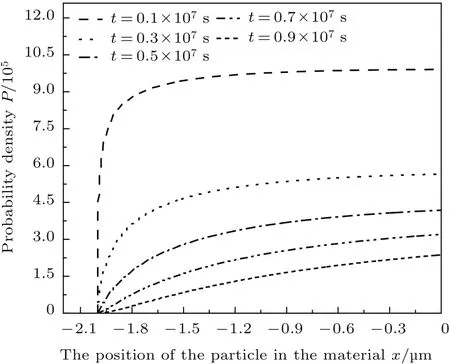
圖2 不同時刻勢阱A中概率總量隨位置變化1.5×10?7J/m2)Fig.2.The probability density variation with position in potential well A

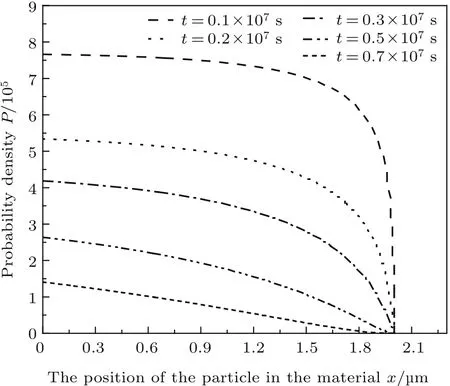
圖3 不同時刻勢阱B中概率總量隨位置變化2.5×10?7J/m2)Fig.3.The probability density variation with position in potential well B

由圖2和圖3可知,在初始時刻,材料A,B中距材料表面[1.8×10?6,0]m范圍內各處的粒子到達材料表面的概率幾乎相同,且都比較大.隨著時間的增加,同一位置的粒子,其到達材料表面的概率在逐漸減小;同一時刻,不同位置的粒子,越接近材料表面的粒子可以到達材料表面的概率相對越大,即越容易到達材料表面.這是因為在磨損初期,材料內粒子較活躍,相對容易被磨損掉而成為磨屑.隨著時間的增加,磨損趨于穩定,離表面較遠的粒子需受振動傳遞及一些力的影響,才能到達材料表面,而材料近表面的粒子由于直接受到外界振動的影響,所以較材料內部粒子更活躍,因此,更容易被磨損掉.總體來看,隨時間的增加,材料總磨損率減小,磨損減輕.這與微動磨損理論[1]中,隨著磨損的進行,有磨屑第三體的產生,磨屑起到潤滑作用,使磨損減輕這一結論相符合.

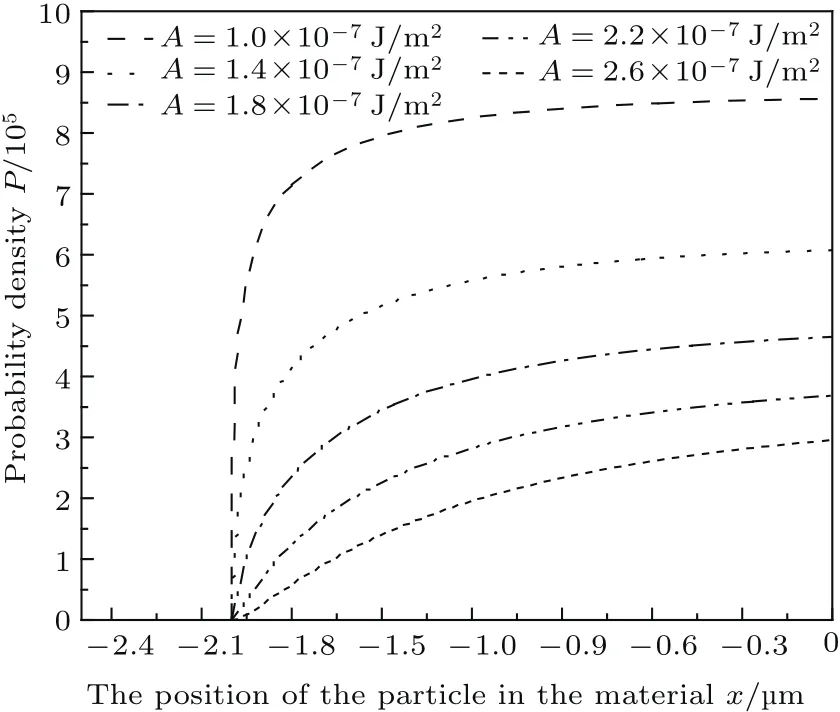
圖4 材料A粒子在不同勢阱寬度中概率密度隨位置的變化(t=0.3×107s,勢阱參量即A的值影響勢阱寬度)Fig.4.The probability density variation with position in the A material(t=0.3×107s,the potential well parameteraffects the width of the potential well).

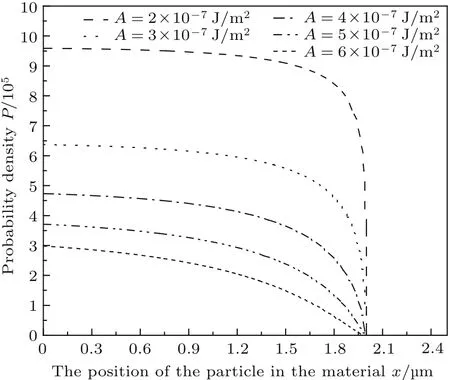
圖5 材料B粒子在不同勢阱寬度中概率密度隨位置的變化(t=0.1×107s,勢阱參量即A的值影響勢阱寬度)Fig.5.The probability density variation with position in the B material(t=0.1×107s,the potential well parameteraffects the width of the potential well).

將圖2和圖4與圖3和圖5對比可得,距材料表面相同位置的粒子在同一時刻、相同勢阱寬度的情況下,材料B中的粒子運動到材料表面的概率明顯小于材料A.這是因為在摩擦副系統中,材料A是軟材料,材料B是硬材料,由于材料本身性質的不同,軟材料的粒子更容易由于微動而轉移到達其表面,從而被磨損成為磨屑.

對(19)和(20)式中的概率密度分布函數PA(x0,x,t)和PB(x0,x,t)在摩擦副系統中材料A所研究的總范圍[?2×10?5,0)m和材料B所研究的總范圍(0,2×10?5]m內分別進行積分,可得在微動條件下材料內部的粒子從t時刻單位時間內運動到材料表面的總概率,即磨損率,表示為

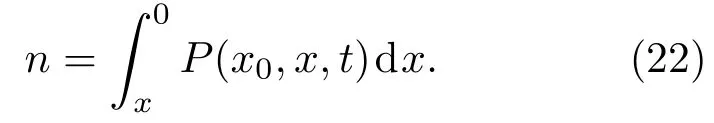
根據(22)式,結合(19)和(20)式并代入數據計算可得磨損率大小.僅改變磨損時間,計算多組數據,繪圖可得摩擦副系統中材料內粒子在勢能函數不變時磨損率隨時間的變化曲線,如圖6所示.同樣,僅改變表征勢阱寬度的參量可得摩擦副系統中材料內粒子在相同時刻處在不同勢阱中磨損率隨勢阱寬度的變化曲線,如圖7所示.

從圖6可以看出,摩擦副系統在磨損過程中兩材料A,B的磨損率均隨時間的增加而減少,而且剛開始減小得快,隨后較慢并逐漸趨于穩定,這與微動摩擦學理論中的第三體理論[1](在磨損過程中形成磨屑作為第三體起到潤滑作用而使磨損減輕,最后趨于平衡)相符合.從圖7可以看出,在磨損過程中,摩擦副系統中兩材料A,B的磨損率均隨¨U(x)的增大而減小,即隨著勢阱寬度的變小而減小.這與前邊概率分布隨勢阱寬度變化呈現出相同的規律,與勢阱寬度變化引起勢阱對粒子束縛力變化的現象相一致.分別對圖6和圖7中材料A,B的兩條曲線進行對比可得:在摩擦副系統中材料A的磨損率始終大于材料B,這是因為這里選取的材料A為軟材料,材料B為硬材料,在磨損過程中,由于材料本身性質的不同,軟材料表面更容易發生磨損,材料中粒子更容易被磨損掉.但不管軟材料還是硬材料,呈現的變化趨勢相同.

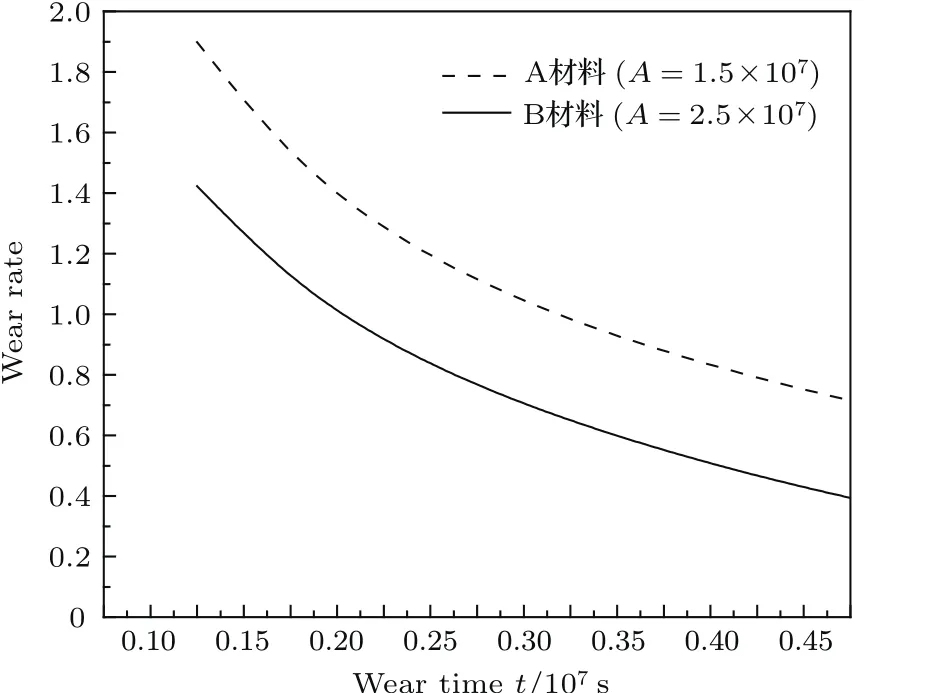
圖6 勢阱中磨損率隨時間的變化Fig.6.The change of wear rate in a potential well with time.

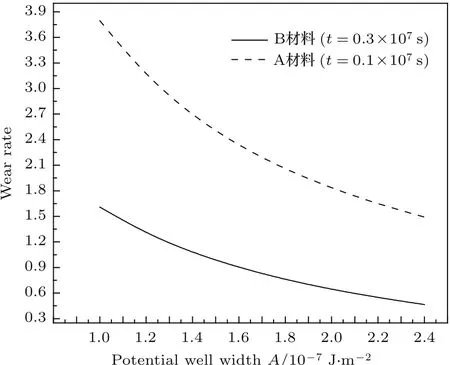
圖7 材料中磨損率隨勢阱寬度的變化Fig.7.The change of wear rate in material with potential well width.

3.3 模型延伸分析

摩擦副間粒子相互作用的勢能函數,其函數圖像的形狀與多種因素有關,包括接觸載荷和滑移距等.這里通過建立勢能函數和接觸載荷的關系,可進一步得出其對磨損率的影響.

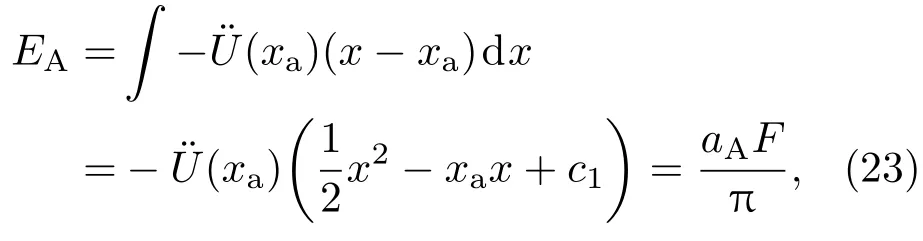
材料B的粒子在勢阱B中有

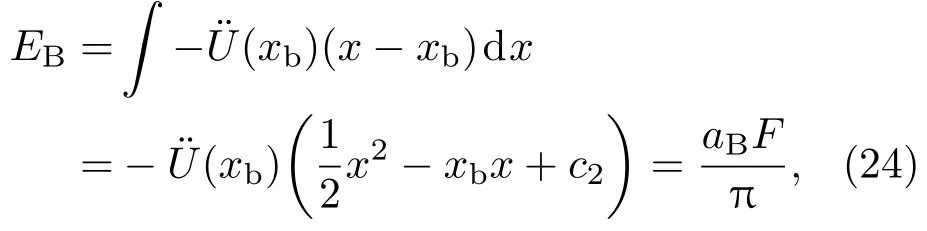
其中,EA和EB為兩材料A,B內粒子的勢能;aA和aB分別為兩材料A,B的晶格系數;F為載荷正壓力;c1和c2分別為兩材料A,B的積分常數.由(23)和(24)式可看出,對于材料內相同位置的粒子,與勢阱寬度有關的量與載荷正壓力F呈線性反比關系.由越大,勢阱寬度越小,磨損率越小可知,載荷正壓力越小,磨損率越小,反之載荷正壓力越大,磨損率越大.磨損率隨載荷正壓力的變化如圖8中的理論曲線所示,其變化趨勢與磨損率隨勢阱寬度的變化趨勢相同.開始階段,接觸載荷較低,微動磨損率變化幅值很小;當接觸載荷增加到臨界接觸載荷后,微動磨損率隨載荷的增加而急劇增大.

4 試驗驗證

通過以上內容的論證和計算,推導出了磨損率隨勢壘寬度和時間的變化關系,為了驗證其合理性,將理論結果和試驗結果[17]進行對比,如圖8所示.

從圖8可以看出,微動磨損率隨載荷的增加而呈指數增長,理論計算結果與試驗所得曲線的趨勢基本一致,這進一步說明了理論的正確性.當載荷正壓力較大時,理論計算結果和試驗曲線有一定的差異,這主要是由于在理論計算中沒有考慮邊界條件等的影響.因磨損率表示單位時間材料內的粒子運動到材料表面的概率,故從材料磨損率能直接反映材料的磨損量.圖8中理論曲線所反映的結論與有關磨損量隨載荷變化的試驗分析結果[18?21]相符合,從而也進一步證明了所得理論模型的準確性.

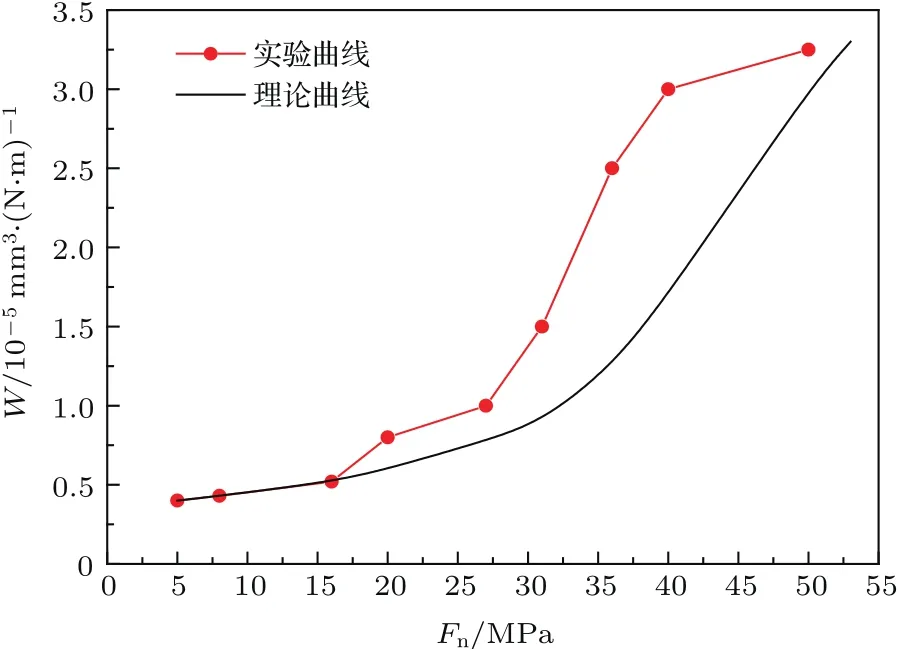
圖8 載荷正壓力磨損率的理論計算值與試驗結果的比較Fig.8.The comparison between theoretical calculation and experimental of load positive pressure-wear rate.

5 結 論

建立了微動磨損過程摩擦副系統中粒子運動的非平衡統計理論模型,計算出了粒子在任意時刻從材料內部運動到表面的概率密度分布函數,求得了材料內粒子從t時刻,單位時間內運動到材料表面的總概率,即磨損率,進一步直接反映出材料的磨損量.同時,將理論模型應用于由金屬材料Mg和Fe組成的摩擦副系統,從微觀角度出發說明了磨損率隨時間的變化和磨損率與勢阱寬度的關系.結果表明:在相同摩擦副系統中,磨損率隨時間的增大而減小;在相同時刻,勢阱寬度不同的摩擦副系統,磨損率隨勢阱寬度的減小而減小.將勢阱寬度與磨損率關系轉化成載荷正壓力與磨損率的關系,與已有試驗數據結合對比,得出相同的結論,并與微動摩擦學中已有的磨損理論所得結論相符合,說明了該理論模型的正確性.

此模型適用于探究不同材料在微動過程中磨損率隨一些影響因素的變化,從而達到對工業生產中一些儀器器件在微動磨損方面造成破壞的壽命預測,減少未知因素造成的損失.