反應擴散系統中反螺旋波與反靶波的數值研究?
倪之瑋 李新政 白占國 李燕
(河北科技大學理學院,石家莊 050018)
1 引 言
螺旋波斑圖是非線性系統中自組織形成的時空有序結構,是自然界中最常見和最基本的一種遠離平衡態的斑圖形式,它廣泛地存在于自然界和各實驗系統中[1?5],根據傳播形式可分為螺旋波(spiral)和反向螺旋波(antispiral).螺旋波(運動形式由波頭向外傳播的螺旋波)由于其廣泛存在和容易形成被人們所熟知,國內外學者已對其進行了系統的實驗及理論研究,并發表了大量的研究結果.人們通過分析多個系統中的單臂螺旋波的性質及其動力學行為,系統地研究了單臂螺旋波的破缺機制和控制方法[6?12],并對復雜的多臂數螺旋波和超級螺旋波也從理論模擬和實驗上進行了多方面的研究[13?19].而反螺旋波(運動形式由外向波頭反方向傳播的螺旋波)直到2001年Vanag和Epstein[20]在BZ-AOT化學反應系統中發現,才被命名,隨后開始引起人們的注意與研究.Gong和Christini[21]通過模擬發現反應擴散系統在霍普失穩附近會出現反螺旋波;Wang等[22]發現弛豫振蕩介質中遠離霍普失穩時以及單相反應擴散系統在臨近霍普失穩時也可以自發出現反螺旋波;Nicola等[23]利用復Ginzburg-Landau理論方程討論了反應擴散系統在霍普失穩附近產生螺旋波與反螺旋波的區別;Qian等[24]利用耦合FitzHugh-Nagumo(FHN)模型研究了多普勒失穩造成穩定反螺旋波到湍流態的演化.鑒于反螺旋波的研究起步較晚,目前相關研究結果相對較少.研究不同失穩時系統出現的反螺旋波以及反螺旋波的多樣性,將有助于人們對反螺旋波的了解.
本工作采用三變量Brusselator擴展模型,分析了反應擴散系統反螺旋波與反靶波的產生機制與時空特性,并對反應擴散系統中的反螺旋波與反靶波以及多臂反螺旋波的形成及其轉化過程進行了數值分析,其研究結果對于豐富和深入理解反螺旋波和反靶波的理論具有一定的參考意義.
2 理論模型
目前,用于研究螺旋波斑圖的理論模型主要有復Ginzburg-Landau方程、三變量Purwins模型、Barkley模型、FHN模型和B?r模型等.本工作采用三變量Brusselator擴展模型[25],其無量綱的形式如下:
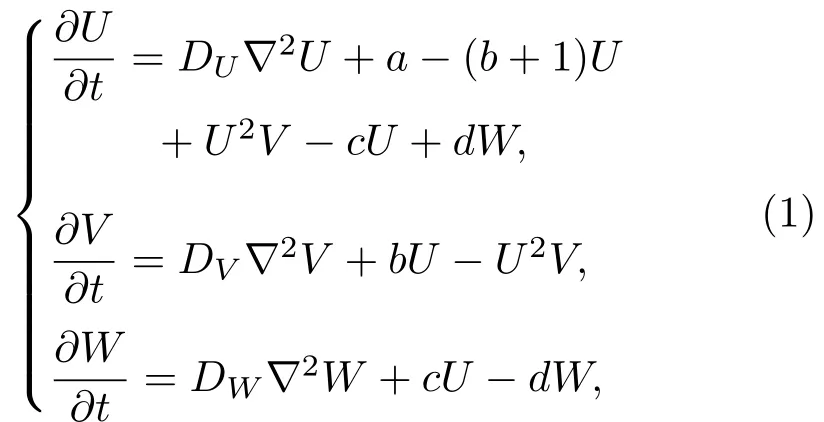
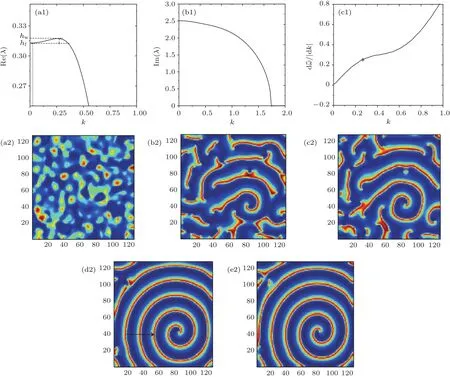
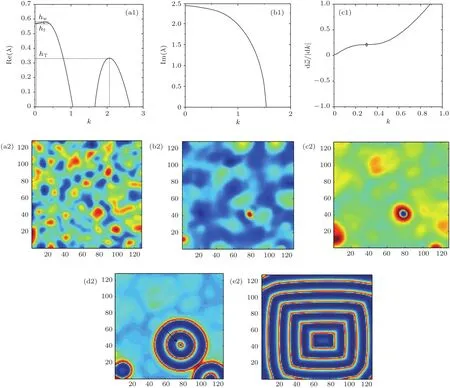
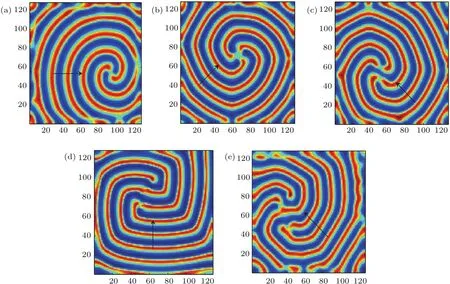
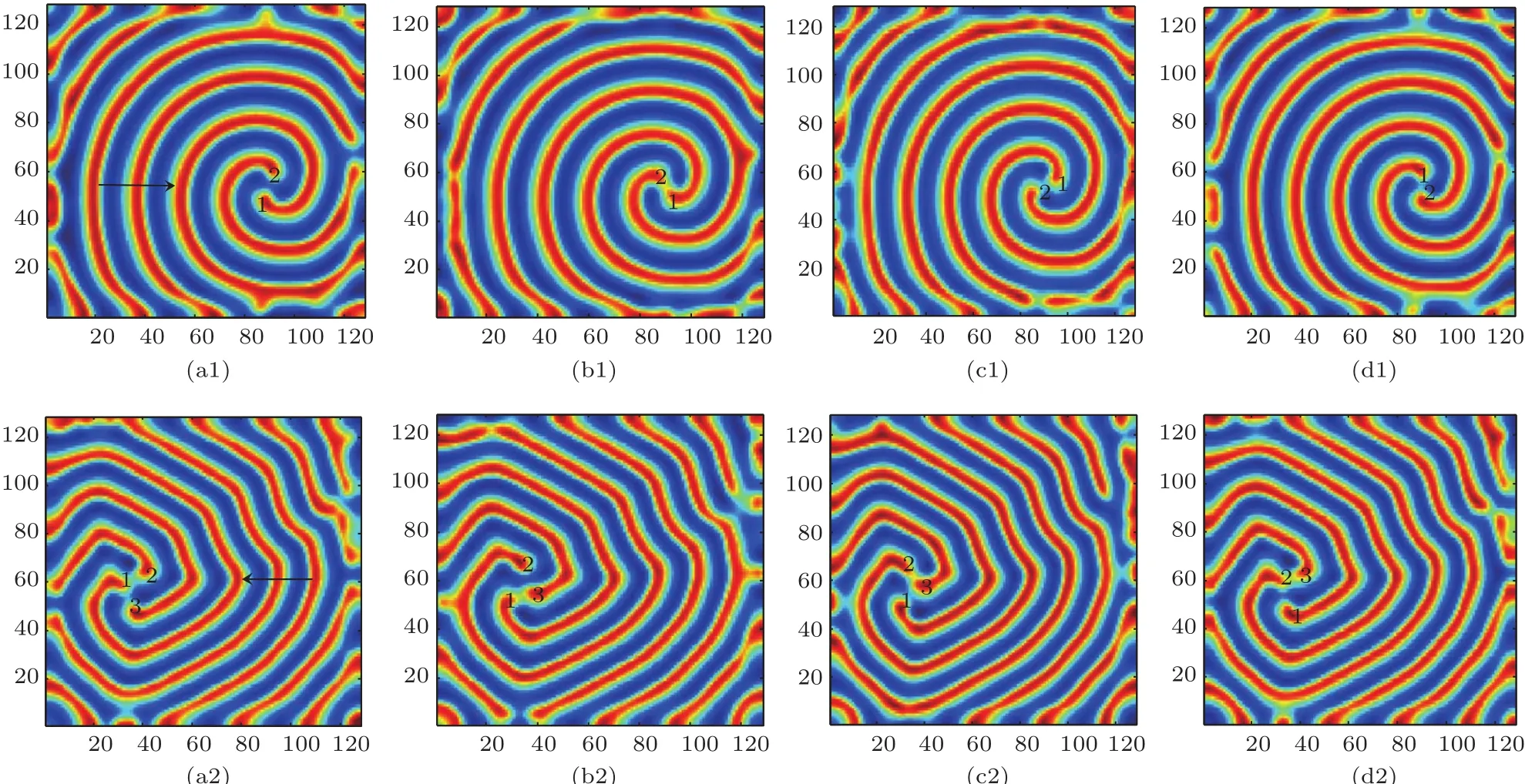
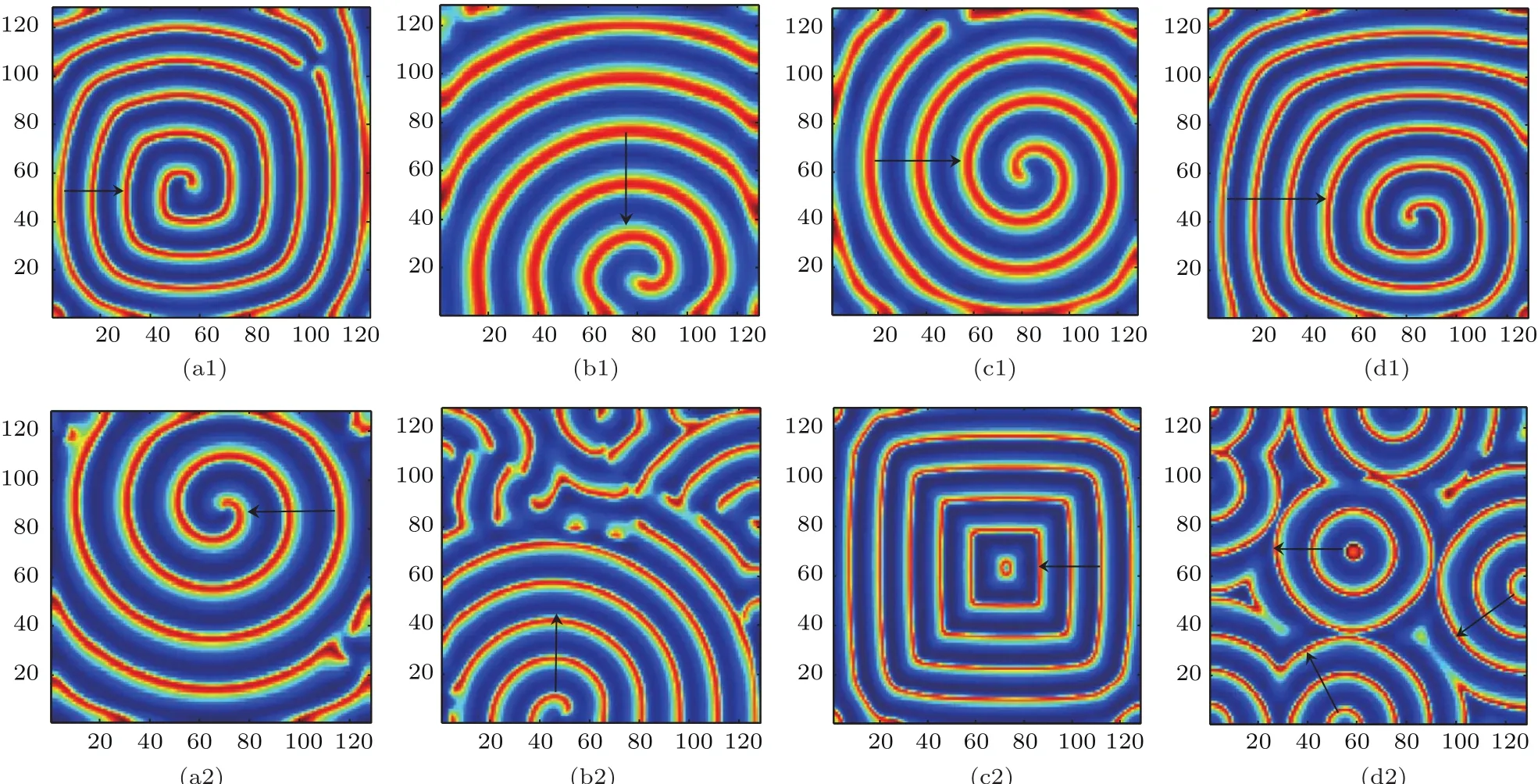
式中,U,V和W分別為活化子和禁阻子以及不活躍中間物質的濃度;DU,DV,DW分別表示三個變量的擴散系數(DU 解此特征方程可以得到色散關系: 利用色散關系可以判斷系統的失穩特性,進而可知系統形成斑圖的時空特征.當Im(λ)=0,Re(λ)=0(k=kT=0)時,系統發生圖靈失穩,形成空間上周期性分布的靜態斑圖;當Im(λ) =0,Re(λ)=0(k=0)時,系統經歷霍普失穩,形成隨時間周期變化的均勻動態斑圖;當Im(λ) =0,Re(λ)=0(k=kw=0)時,系統經歷波失穩,產生時間和空間上都具有周期性的動態斑圖. 在本文的數值模擬中,采用歐拉向前差分的方法進行積分,數值模擬在一個含有N×N(128×128)個格子的二維平面上進行,時間積分步長為?t=0.01個時間單位,邊界條件選用零流邊界條件,為確保其穩定性所有結果的積分時間均超過2000個時間單位. 非線性系統發生霍普失穩或波失穩時系統的均勻性會遭到破壞,從而引起物質濃度的變化,系統形成隨時間變化的空間動態斑圖.模擬研究發現反應擴散系統不僅在霍普失穩、波失穩附近產生反螺旋波,并且在霍普失穩與波失穩共同作用下也可以形成多種反向螺旋波.圖1是系統參數(a,b,c,d,Du,Dv,Dw)在(2.0,7.0,1.0,1.0,0.5,1.0,8.0)附近時,形成的單臂反螺旋波.從色散曲線進行分析,可以看出系統在經歷霍普失穩的同時發生波失穩,且霍普模的強度hf大于波失穩處模的強度hw,因此霍普失穩占主導地位,而波失穩相對較弱,系統可形成隨時間和空間周期變化的動態斑圖.由于反螺旋波的群速度vg>0(圖1(c1)),所以其波源成為中心位置的拓撲缺陷點,而由于波的傳播方向由外向內,與螺旋波的方向相反,所以相速度vp<0,因此可判斷反螺旋波的色散關系為負[23,25,26].從反螺旋波的形成過程(圖1(a2)—(e2))可以看出:二維模擬系統首先隨機產生隨時間變化的空間動態點狀斑圖,隨模擬時間的延長,不同動態點狀斑圖間相互碰撞融合,逐漸演化成動態線狀條紋斑圖,由于條紋斑圖不同位置的波速不同,邊緣端點的波速小于中間位置點的波速,條紋逐漸變為蜷曲狀,一個端點形成波頭,在局部形成反螺旋波的初始形態,隨模擬時間的延長最終演化成產生于邊界、波由外向內傳播、消失于中心的單臂反螺旋波.圖1(d2)和圖1(e2)是同一周期中波頭的不同相位,兩圖的時間間隔約為T/4,從圖中可以看出單臂反螺旋波的走向與波頭的相位運動方向相同,均為逆時針,這與所熟悉的單臂螺旋波的情況相反,是波由外向內的反向傳播造成.經過多次模擬發現反螺旋波的波頭在旋轉過程中表現出與螺旋波相同的運動特點,如運動軌跡為定點、圓形、漫游等.此外,系統還可觀察到同向和反向轉動的偶極子反螺旋波對. 圖1 單臂反螺旋波的色散關系曲線及形成過程 (a1)色散的實部Re(λ)曲線;(b1)色散的虛部Im(λ)曲線;(c1)虛部的導數曲線;(a2)—(e2)為單臂反螺旋波的形成過程(模擬時間順序:13.9,577.3,657.7,1279.6,1280.3)Fig.1.Dispersion relation curves and forming process of single-arm antispral:(a1)The real part of dispersion;(b1)the imaginary part of dispersion;(c1)the first derivative of the imaginary part;(a2)–(e2)the forming process of single-armed antispiral(The simulation time sequence is as follows:13.9,577.3,657.7,1279.6,1280.3). 圖2 反螺旋波變量的時空分布 (a)三變量的時間分布(選取時間間隔5000—6000);(b)三變量的空間分布Fig.2.Spatio-temporal distribution of variables:(a)The time distribution of the three variables(The selected time interval is between 5000 and 6000);(b)the spatial distribution of the three variables. 圖3 反靶波的色散關系曲線及靶波的形成過程 (a1)色散的實部Re(λ)曲線;(b1)色散的虛部Im(λ)曲線;(c1)虛部的導數曲線;(a2)—(e2)為靶波的形成過程截圖(模擬時間順序:13.8,75.8,121,200.2,5284.8)Fig.3.Dispersion relation curves and forming process of antitarget wave:(a1)The real part of dispersion;(b2)the imaginary part of dispersion;(c1)the first derivative of the imaginary part;(a2)–(e2)the forming process of antitarget wave(The simulation time sequence is as follows:13.8,75.8,121,200.2,5284.8). 利用u,v,w三個變量的濃度隨時間和空間的變化對單臂反螺旋波的時空特性進行分析.從變量隨時間和空間的變化曲線(圖2)可以看出:三者均隨時間做周期性振蕩,在空間上也是周期性分布的,且兩圖中三變量的峰值出現的位置不同,這是由于三變量具有不同的時間尺度和擴散速度造成的.從變量的時空特征可以判斷反螺旋波是一種時間上振蕩,空間上呈周期性分布的時空斑圖. 系統不僅可以生成反螺旋波,還可以生成向里傳播的反靶波.圖3是系統參數(a,b,c,d,Du,Dv,Dw)在(2.0,7.5,1.0,1.0,0.4,1.0,8.0)附近時,二維模擬系統形成的反靶波斑圖.通過對色散關系曲線分析,發現系統在經歷霍普失穩和波失穩的同時還經歷了圖靈失穩,并且霍普模的強度hf和圖靈模的強度hT遠大于波失穩處模的強度hw,因此系統以霍普失穩和圖靈失穩為主,而波失穩相對較弱,系統在多種失穩的共同作用下可形成復雜運動形式的動態斑圖.由于反靶波的群速度vg>0(圖3(c1)),所以中心為波源,與螺旋波和反螺旋波的位置相同;又因波的傳播方向與反螺旋波相同——由外向內傳播,所以相速度vp<0,由此可判斷反靶波的色散關系為負.經研究發現反靶波的形成過程與反螺旋波不同,二維模擬系統首先在某些區域出現強度周期變化的無規則點狀斑圖,空間位置基本不變.隨模擬時間延長,其中幾個區域周期變化的點狀斑圖逐漸突顯,并影響到整體,二維模擬空間在這幾個區域逐漸形成靶源,并形成由外向靶心傳播的多個自持續反靶波,多個反靶波間通過相互影響,最終二維模擬系統形成單一中心的反靶波,但由于受模擬邊界及空間位置的影響,形狀為圓形的反靶波最終演化成方形反靶波. 通過大量模擬發現:在一定條件下單臂反螺旋波也可以轉化成反靶波,此過程初始階段與二維系統直接形成反靶波不同,而與反螺旋波的過程相同.從圖4可以看出,系統首先由無規則動態點狀斑圖演化成動態條紋斑圖,進而形成單臂反螺旋波斑圖,但所形成的反螺旋波斑圖的波頭較為特殊,在隨模擬時間延長過程中,波頭區域會逐漸增大,在旋轉過程中由于其波速較低,會與反螺旋波的臨近部位相碰撞,并在此位置截斷反螺旋波,原波頭區域會形成一個自持續的周期性靶源,從而在局部區域形成不規則的反靶波,隨模擬時間延長,二維模擬系統最終形成反靶波斑圖. 圖4 單臂反螺旋波向反靶波轉化過程(模擬時間順序:702.7,2115.8,3605,4164.9,4739.4)Fig.4.Conversion process of single-armed antispiral to anti-target wave(The simulation time sequence is as follows:702.7,2115.8,3605,4164.9,4739.4). 通過數值模擬獲得了單臂、雙臂、三臂等多種不同臂數的反螺旋波斑圖.圖5為二維模擬系統獲得的雙臂到六臂的反螺旋波斑圖.從圖5可以看出,波傳播方向均由外向里,波頭的相位運動方向與反螺旋波的走向相同,旋轉方向隨機,可為順時針或逆時針方向,除三臂反螺旋波的波頭順時針轉動外,其余則為逆時針轉動.研究發現,反螺旋波隨臂數的增加,不僅波頭的動力學行為更加復雜,而且中心區域的半徑也逐漸增大,這與實驗系統系統對多臂螺旋波研究結果相一致[27]. 圖5 不同臂數反螺旋波斑圖(其余固定參數:a=3.0;b=11.39;c=d=1.0) (a)雙臂(Du=0.5,Dv=1.0,Dw=23.0);(b)三臂(Du=0.6,Dv=1.0,Dw=25.0);(c)四臂(Du=0.7,Dv=1.0,Dw=25.0);(d)五臂(Du=0.45,Dv=1.0,Dw=40.0);(e)六臂(Du=0.6,Dv=1.0,Dw=26.0)Fig.5.Various kinds of multi-armed antispiral patterns(Parameters:a=3.0;b=11.39;c=d=1.0):(a)Two arms(Du=0.5,Dv=1.0,Dw=23.0);(b)three arms(Du=0.6,Dv=1.0,Dw=25.0);(c)four arms(Du=0.7,Dv=1.0,Dw=25.0);(d) five arms(Du=0.45,Dv=1.0,Dw=40.0);(e)six arms(Du=0.6,Dv=1.0,Dw=26.0). 在模擬多臂反螺旋波過程中,發現不同臂數反螺旋波的波頭運動規則不同,并且波頭間的碰撞順序與波頭的旋轉方向有關.圖6是雙臂與三臂反螺旋波的波頭逆時針旋轉運動的情況,可以看出:波頭的轉動方向都與波的走向相同,雙臂反螺旋波的動力學行為相對比較簡單(圖6(a1)—(d1)),在T/2周期內兩臂的波頭不斷發生碰撞和遠離,且繞著同一個中心點做周期性運動,旋轉過程中每半個周期兩旋轉臂的波頭碰撞一次,兩個波頭位置總是關于中心點對稱分布,這就意味著雙臂反螺旋波的兩個波頭相位差始終保持π;三臂反螺旋波的波頭具有非常復雜的動力學過程(圖6(a2)—(d2)),由于相鄰兩臂的相位差為2π/3,所以旋轉臂失去了對稱性,在T/3周期內波頭碰撞兩次,它的三個波頭端點兩兩相互碰撞,順序為1-3-2-1的逆時針排序.由于多臂螺旋波的波頭在不停地碰撞和遠離,所以隨著臂數的增加,四臂、五臂和六臂反螺旋波的波頭運動情況更為復雜,并且發現隨臂數的增加,波頭的旋轉運動周期逐漸增大,其原因可能與中心區域的旋轉半徑有關. 通過觀察不同情況的多臂反螺旋波發現,在一定模擬條件下多臂反螺旋波經歷一段時間后,其中的一個旋轉臂會逐漸遠離波頭中心區域,并逐漸消失,系統形成一個新的臂數少一的反螺旋波斑圖.圖7是逆時針旋轉的反螺旋波從四臂→三臂的轉化過程,可以看出:四臂反螺旋波中心波頭的旋轉及相互碰撞比雙臂與三臂反螺旋波運動更加復雜,在波頭旋轉運動的過程中其中心會發生緩慢的移動,從而使四臂反螺旋波逐漸失去了空間旋轉不變對稱性;同時由于它的中心四個端點也在不斷地相互作用,造成其中的一個旋轉臂逐漸遠離旋轉中心區域,并在邊界條件的限制下逐漸消失,二維模擬系統形成一個新的三臂反螺旋波.分析其原因主要是由于微擾的作用或者其他條件的影響,使位錯的拓撲荷符號與反螺旋波的拓撲荷符號相反造成的.圖7中四臂反螺旋波為逆時針走向時,因與螺旋波運動方向相反,所以其拓撲荷符號應為負值;而反螺旋波的波頭相位運動方向同為逆時針,因此位錯的拓撲荷符號為正值.此外,還發現多臂反螺旋波在一定條件下可以實現從多臂到單臂的連續轉化. 圖6 雙臂與三臂反螺旋波波頭的旋轉運動情況 (a1)—(d1)雙臂模擬時間順序分別為 3424.5,3425,3425.7,3426.3;(a2)—(d2)三臂模擬時間順序分別為3074.7,3075.3,3075.7,3076.2Fig.6.Rotating motion of the wave tips with two arms and three arms.(a1)–(d1)the simulation time sequence of twoarmed antispiral is as follows:3424.5,3425,3425.7,3426.3.(a2)–(d2)the simulation time sequence of three-armed antispiral is as follows:3074.7,3075.3,3075.7,3076.2. 圖7 四臂反螺旋波向三臂反螺旋波轉化過程(模擬時間順序:2405.9,2529.9,2648.1,2895.8,3190)Fig.7.Conversion process of four-armed antispiral to three-armed antispiral(The simulation time sequence is as follows:2405.9,2529.9,2648.1,2895.8,3190). 由于斑圖的形成與穩定性依賴于參數的選取,因此研究系統參數對圖形的影響非常重要.文中在一定范圍內研究了控制參數a,b以及擴散系數對斑圖的影響:通過對比發現控制參數a,b的連續變化可引起反螺旋波空間尺度的規律變化,隨a的增加反螺旋波逐漸變稀疏(圖8(a1)和圖8(b1)),而隨b的增加反螺旋波逐漸變密集(圖8(c1)和圖8(d1)),并且參數a的可變化范圍遠小于b.擴散系數雖對斑圖的空間尺度沒有明顯的影響,但發現擴散系數Dw持續增加到一定值時,波的傳播方向會發生改變,由向內傳播改為向外,二維模擬系統形成的反螺旋波與反靶波會被螺旋波和靶波所取代(圖8(a2)—(d2)),且隨Dw的增大反螺旋波不僅會轉為同臂數的螺旋波,還可形成不同臂數的螺旋波.利用色散曲線分析其原因發現,隨Dw的增加,系統的波失穩程度逐漸增大,當波失穩達到一定程度時,波速vg為正值,從而導致了系統斑圖屬性的改變.因此得出系統在臨界波失穩附近時可形成反螺旋波和反靶波,而在遠離波失穩時易形成螺旋波和靶波. 圖8 系統參數變化對斑圖的影響 (a1),(b1)a變化時波空間尺度對比(a=1.95,2.05);(c1),(d1)b變化時波空間尺度對比(b=6.5,7.0);(a2),(b2)反螺旋波到螺旋波的轉變(Dw=6.0,19.0);(c2),(d2)反靶波到靶波的轉變(Dw=8.0,10.0))Fig.8.In fluence of system parameter variation on the pattern:(a1),(b1)Wave space scale changes induced by parameter a(a=1.95,2.05);(c1),(d1)wave space scale changes induced by parameter b(b=6.5,7.0);(a2),(b2)the transformation of antispiral to spiral induced by parameter Dw(Dw=6.0,19.0);(c2),(d2)the transformation of antitarget wave to target wave induced by parameter Dw(Dw=8.0,10.0). 本文利用三變量Brusselator擴展模型對反應擴散系統中反螺旋波和反靶波進行了數值研究,并與螺旋波的研究結果進行了對比,發現其形成機制和時空特性具有與螺旋波相同的特征,如失穩特征、時空的周期性、波頭運動軌跡的多樣性等,同時還發現反螺旋波的波頭旋轉方向與波的走向相同這一點與螺旋波不同,考慮其原因是反螺旋波由外向內傳播方式造成的.除霍普失穩外,系統得到在超臨界波失穩附近生成的多種反螺旋波.通過改變參數獲得了多種不同臂數的反螺旋波,發現隨臂數的增加,波頭的運動特點更為復雜,且波頭的旋轉周期隨臂數的增加逐漸增大.在一定的模擬條件下,由于受微擾及邊界條件因素的影響,多臂數的反螺旋波可以向臂數少的反螺旋波發生轉變,并可實現單臂反螺旋波到反靶波的轉化.通過研究系統參數對斑圖的影響發現:控制參數a,b對反螺旋波與反靶波的空間尺度影響比較明顯,而與參數a,b持續增大造成波空間尺寸變化的效果相反;擴散系數Dw的持續增加會造成波失穩程度的增大,并導致波速符號發生變化,從而系統斑圖出現反螺旋波到螺旋波以及反靶波到靶波的轉變.本文的研究結果不僅豐富了反螺旋波的相關理論,對于深入研究反螺旋波和螺旋波的相互聯系也具有重要的借鑒作用.

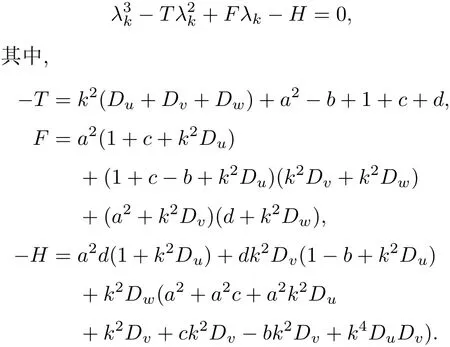
3 數值模擬結果與分析
3.1 反螺旋波的形成機制

3.2 反靶波的形成機制
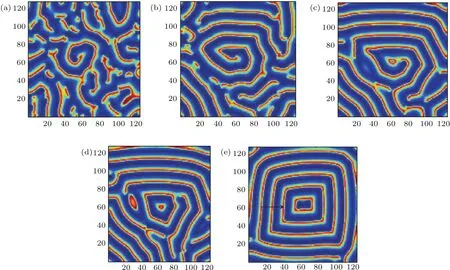
3.3 多臂反螺旋波的時空特性及其轉化

3.4 系統參數對反螺旋波和反靶波的影響
4 結 論

