基于多點預瞄最優控制的智能車輛路徑跟蹤

黃海洋 張建 王宇 王御 劉金波

（中國第一汽車集團有限公司智能網聯開發院，長春 130011）

主題詞：LQR 道路預瞄模型 路徑跟蹤 智能車輛

1 前言

路徑跟蹤作為自動駕駛系統中的關鍵執行層控制技術，是影響智能車輛安全性與舒適性的關鍵技術[1-3]。常見的路徑跟蹤方法按照使用模型不同可分為基于幾何/運動學模型的方法和基于動力學模型的方法，其中基于幾何/運動學模型的方法，通常將車輛簡化為四輪機器人剛性結構，由于相對簡單計算量小，已有較多實車應用，如名古屋大學的自動駕駛開源項目Autoware中使用的純跟蹤方法[4]。基于動力學模型的方法，考慮車輛輪胎側偏等動力學特性，通常結合最優控制理論，如線性二次型調節器（LQR）[5]、模型預測控制（MPC）[6]等。百度的自動駕駛開源項目Apollo中橫向控制器即提供了LQR和MPC兩種方法[7]。LQR方法未考慮預瞄前方目標路徑，易出現跟蹤偏差較大問題；MPC方法需要消耗大量計算資源，在車輛嵌入式控制器的計算環境中難以實現。而基于預瞄的LQR控制方法[8]，既能夠綜合考慮前方路徑特征，又不需要在線優化求解占用大量計算資源，具有較強的嵌入式環境實車應用價值。

因此，本文在文獻[8]LQR預瞄控制方法的基礎上，提出了一種新型基于多點預瞄的最優路徑跟蹤控制方法，改進了道路模型中的預瞄偏差計算方式，以及采用離線計算最優增益的方法，提高了算法的適應性及實時性，更加適合實車路徑跟蹤控制應用。

2 車輛及道路預瞄模型

2.1 車輛動力學模型

本文采用的車輛動力學模型如圖1所示，假設車輛是一個在平面內沿一定速度向前行駛的剛體，可通過前輪轉角進行橫擺旋轉和側向平移運動。

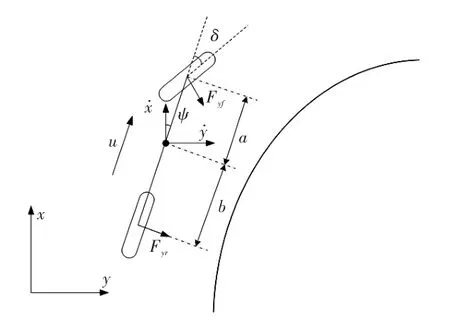
圖1 車輛動力學模型

通過如圖1所示的幾何關系，可推導出前后軸的側偏角αf、αr關系式：

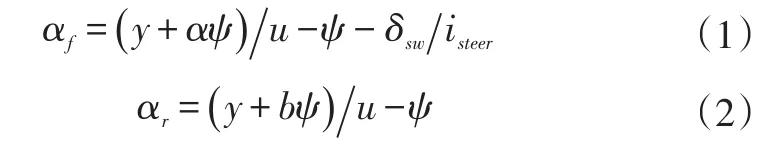
式中，y為車輛橫向位置；a、b分別為車輛質心到前后軸的距離；ψ為車輛航向角；u為車輛縱向速度；δsw為轉向盤轉角；isteer為轉向傳動比。

然后由車輛前后軸的側偏剛度Cf、Cr,可知前后軸的側向力Fvf、Fvr:

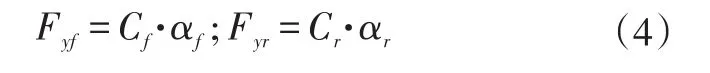
最后，根據牛頓第二定律進行側向力和橫擺力矩分析即可得到式（5）所示的動力學狀態方程。

式中，

式（5）狀態方程為連續量，在控制器中采用的是離散數字控制，需要根據實際采樣時間T對狀態方程進行離散化處理，如式（6）所示。

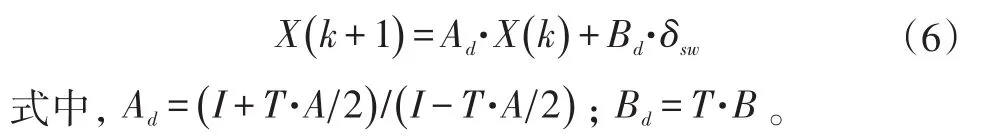
由此狀態方程即可確定車輛在一定速度下轉向盤轉角作為控制量，對車輛橫向位置及橫擺角速度狀態產生的影響。

2.2 道路預瞄模型

圖2（a）所示的為文獻[8]所使用的道路預瞄模型，以道路在局部坐標系下的未來n個周期的參考y軸方向橫向偏移作為道路狀態量，當前車輛在局部坐標系中的橫向坐標為y，朝向角為ψ，假設車輛縱向速度u恒定，當前車輛坐標為y，第一個道路狀態量即為yr0，第二個狀態量即車輛沿x軸方向移動uT后，對應的道路y坐標，即為圖中的yr1，以此類推再下一周期同樣x向移動uT，狀態量變為yr2，yr3，yrn。

此模型采用的局部坐標系方向固定不變，車體坐標系與局部坐標系夾角位置關系隨著車輛運動不斷變化，當車輛朝向角與x軸夾角過大時，車輛的每一時刻x向參考位置的變化將與uT差別較大，使得算法對于這種情況的適應性較差。因此本文的局部坐標系直接采用車體坐標系作為參考，車輛的初始y向坐標為0，航向角ψ也為0，這樣車輛沿x軸的參考位置uT對應橫向參考坐標隨著車體坐標系的不斷變化而不斷變化，縱向速度假設更加合理，算法適應性更強。

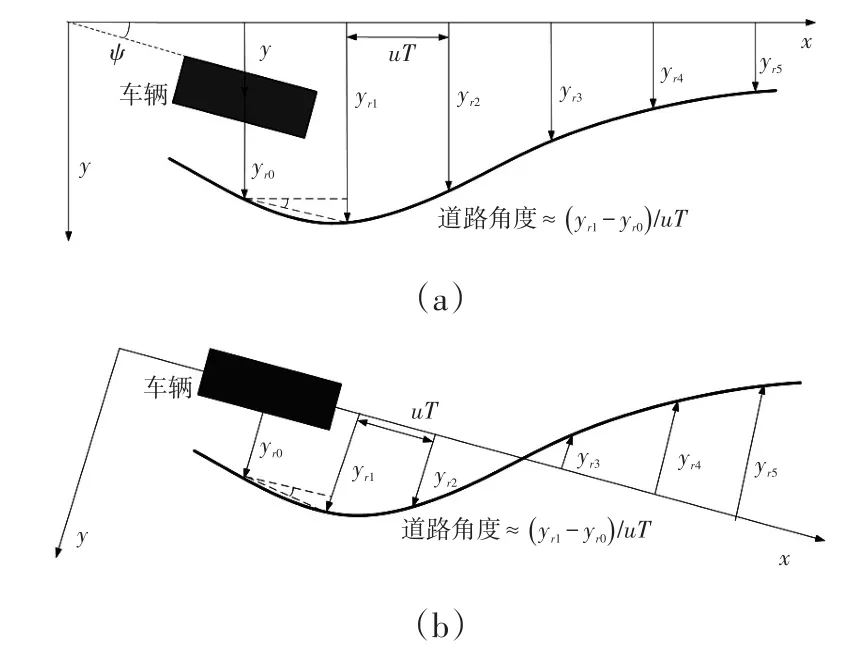
圖2 道路預瞄關系圖

對于車輛而言，k時刻的道路狀態yrn即為k+1時刻的道路狀態yrn-1，只需將前一時刻的道路狀態整體向前移動一個周期，同時補充最后一時刻的狀態yr_n+1，可將道路狀態整理為如下矩陣形式：

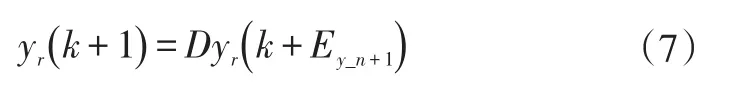
3 LQR最優預瞄控制

整合第2章的車輛模型和道路預瞄模型的狀態方程（6）和（7），可得下式：

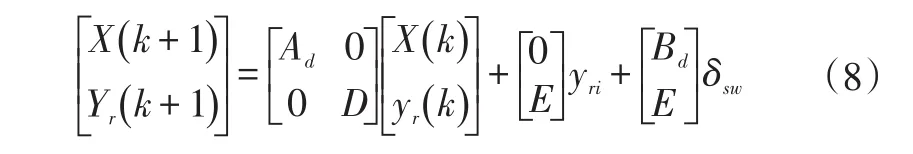
此狀態方程僅描述了車輛和道路間狀態量的變化關系，而車輛和道路則需要通過式（9）所示的目標函數產生關聯：

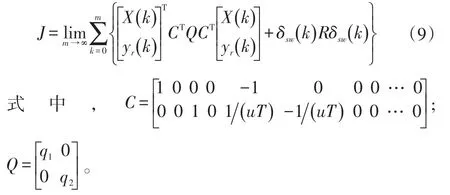
該目標函數為LQR標準的二次型形式，一共包含兩項，第一項目標為路徑跟蹤的橫向與角度的綜合偏差，C矩陣的第一行與式（8）的狀態相乘，即連接了車輛的y軸坐標與道路參考點的y軸坐標差，得到車輛橫向偏差；第二行連接了車輛的航向角與道路朝向角的差，得到車輛角度偏差，同時Q矩陣中的兩個元素q1和q2決定了橫向偏差與角度偏差的權重；第二項表示控制量轉向盤轉角的懲罰項，目的為減少轉向盤轉角輸出，提高系統穩定性，R為該項權重標量。

由上述目標函數和線性狀態方程，即可構成標準的離散LQR控制問題，從而求得由最優增益K和狀態量構成的最優控制量u(k)：

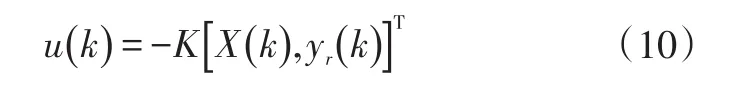
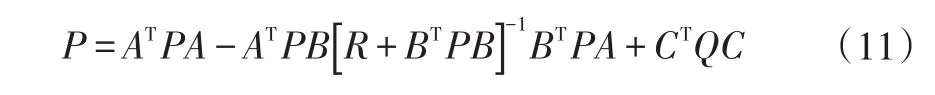
當道路預瞄窗口較大時，上述矩陣維數將明顯增多，求解黎卡提方程將消耗較多計算資源，在嵌入式硬件環境中實時求解難度較大。通過對最優增益矩陣中的元素進行分析，可以發現只有車速u是動態變化的，其他元素均為車輛固有參數，因此，本文采用離線計算不同速度u下的增益矩陣K，然后通過在線查表的方式使用與當前車速u最鄰近的離線增益K，然后與當前車輛狀態、道路狀態按式（10）計算即可獲得控制輸出轉向盤轉角，大幅提升算法實時性。

4 仿真及實車驗證

4.1 仿真結果

為驗證本文算法的跟蹤精度與算法實時性，在CarSim和Simulink聯合仿真的環境下，將本文方法與文獻[9]所提出的模型預測控制方法進行了對比測試，仿真對比結果見圖3和圖4。

仿真所使用的為CarSim中的車輛，其質量為1 723 kg，轉動慣量為4 175 kg·m2，質心距前后軸距分別為1.232 m和1.468 m，前后軸側偏剛度分別為119 552 N/rad和109 548 N/rad。

仿真試驗工況選用雙移線軌跡進行車輛路徑跟蹤能力測試。分別選用常規小側向力工況和達到路面附著極限的工況進行仿真，縱向速度分別為60 km/h和80 km/h，路面附著系數為1，控制周期為20 ms，MPC控制器的預測時域和控制時域均為50，權重矩陣Q和R的取值與文獻[9]中保持一致；本文LQR控制器預瞄周期也為1s，權重矩陣系數q1=0.001，q2=0，R=1。

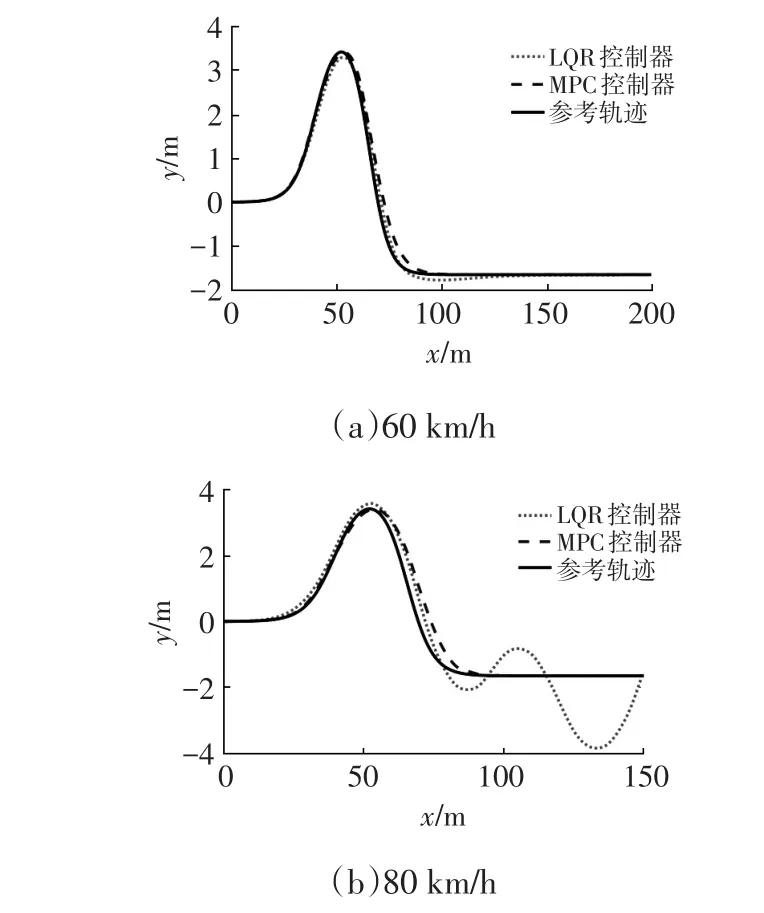
圖3 路徑跟蹤仿真結果曲線

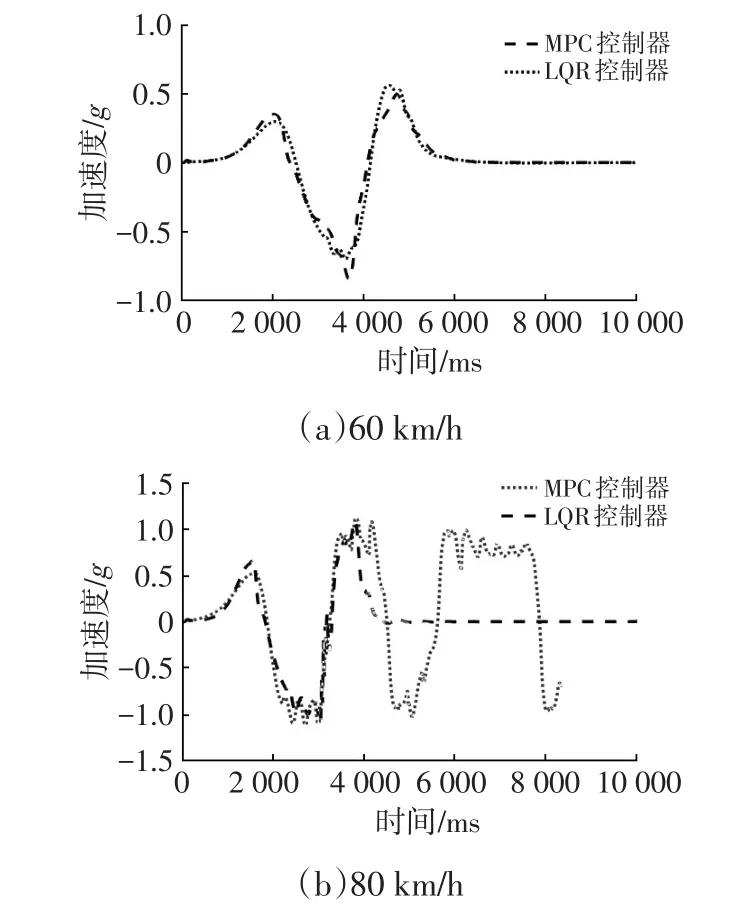
圖4 側向加速度仿真結果曲線

從路徑跟蹤結果中可以看出60 km/h時LQR控制器與MPC控制器均能較好的跟蹤目標路徑，其中LQR控制器的最大跟蹤偏差為0.36 m，而MPC控制器的最大跟蹤偏差為0.64 m；而圖4中可以看出最大側向加速度約為0.7g，尚未達到路面附著極限，提出的LQR控制器能夠較好地跟蹤目標路徑；而在80 km/h的仿真試驗可以看出最大側向加速度達到1g左右，已經達到了路面附著極限，LQR控制器由于不具有MPC控制器的側偏角約束，未能保持車輛穩定性，出現側滑現象。另一方面，本文提出的LQR控制器與MPC控制器仿真單步運行時間分別為8.5 ms和89 ms，LQR方法具有明顯的實時性優勢。由此可見，本文提出的LQR控制器由于具有與MPC控制器相同的優化目標，較為適合實車在附著良好的且未達到附著極限的行駛工況下進行實時控制。

4.2 實車試驗

實車控制器采用的是MicroAutoBox快速原型，LQR控制方法可在該平臺下良好地實時運行，傳感器為RTKIMU組合導航記錄位姿，目標路徑采用人工駕駛過程中錄制組合導航的位置姿態數據，試驗場地為一汽NBD園區內，試驗車輛為紅旗H7摯途試驗車，如圖5所示。

圖5 紅旗H7摯途試驗車

園區內試驗最大車速為30 km/h，覆蓋了長直線、長彎、環島和直角彎等城市道路典型工況，試驗結果如圖6所示，整車最大側向加速度在0.2g以內，橫向控制偏差在0.35 m以內，具有良好的跟蹤精度；以120 s附近的過環島工況為例，轉向盤最大轉角為281°，路徑跟蹤的最大橫向偏差為0.28 m，轉向盤轉動較為平穩。

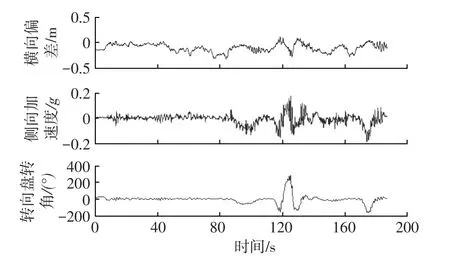
圖6 實車路徑跟蹤結果曲線

圖7所示為LQR控制器在彎曲道路換道工況下的實車路徑跟蹤結果圖，圖7a所示為參考路徑和跟蹤路徑，車速及跟蹤的橫向偏差如圖7b所示，換道時車速約為60 km/h，整體跟蹤偏差在0.3 m以內，最大側向加速度約3.2 m/s2。說明本文方法適合在實車嵌入式實時環境下，平穩地控制車輛實現良好精度的路徑跟蹤功能。

5 結束語

本文針對嵌入式控制器環境下的智能車輛路徑跟蹤問題，基于LQR最優控制方法并采用離線優化的方式，提出了一種基于多點預瞄最優路徑跟蹤控制方法，構建了車輛及道路預瞄模型。仿真及實車試驗表明該方法能夠適應常規工況下實車路徑跟蹤控制，具有良好的跟蹤精度。下一步研究將針對輪胎和路面附著極限工況下，優化輪胎模型，約束最終控制量輸出保證車輛穩定性，提高算法對極限工況的適應能力。

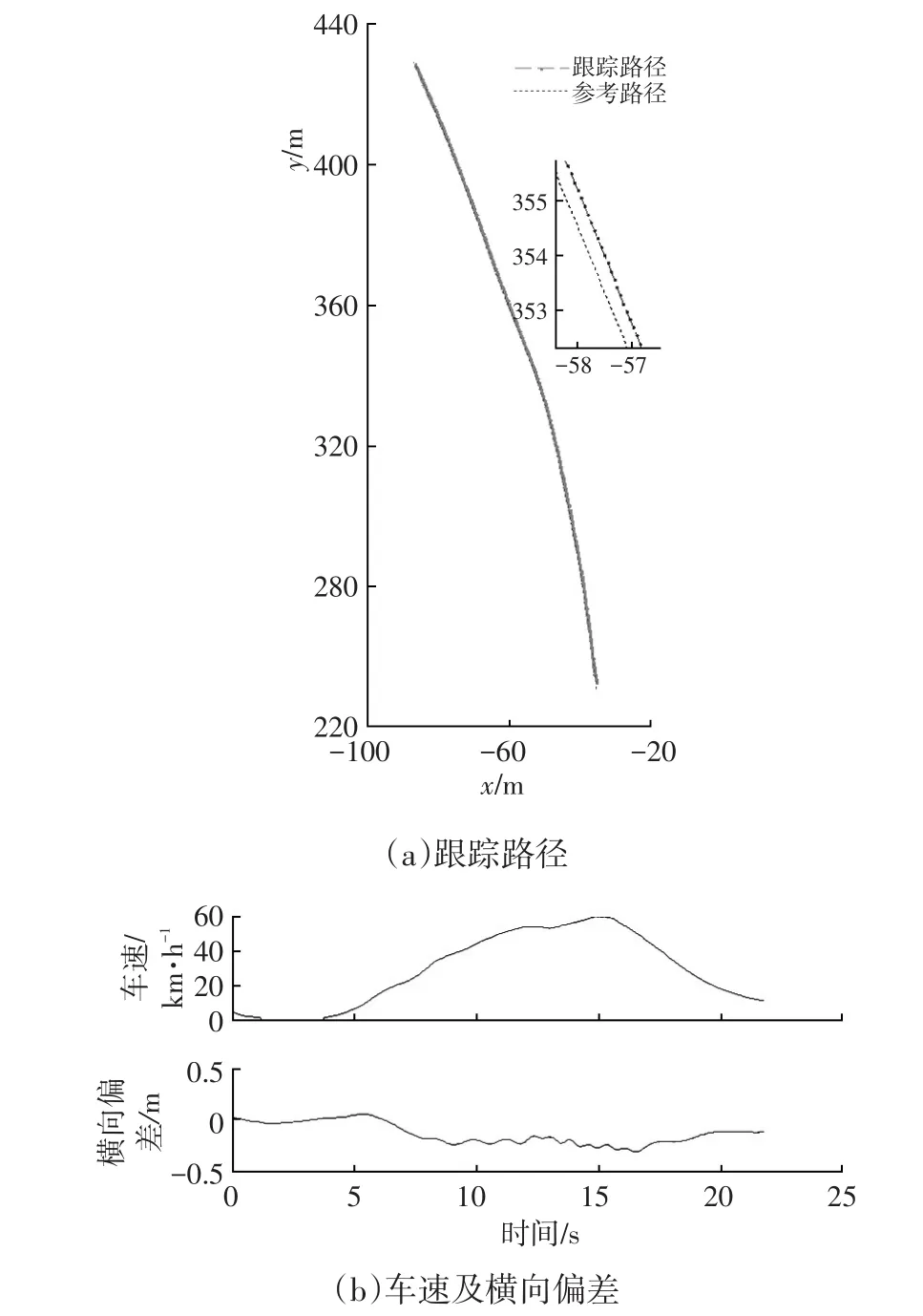
圖7 彎曲道路換道工況路徑跟蹤結果圖