基于非線性模型預測的繩系系統系繩擺振控制

張宇靖， 鐘睿

(北京航空航天大學 宇航學院, 北京 100083)

繩系衛星系統是由系繩連接繩端衛星構成的空間系統[1]。繩系衛星系統表現出了廣闊的應用前景，如空間發電、構建空間結構和拖拽離軌等，是近年來航天研究熱點之一[2]。空間繩系拖拽離軌是借助飛網等機構抓捕，并利用系繩連接主星和目標，由主星機動，實現目標拖拽轉移的新概念在軌操作技術[3-5]。在空間碎片主動移除技術中，空間繩系拖拽離軌是一種較為高效和具有應用前景的技術。

在實際拖拽離軌任務中，系繩的擺動會引起主星的擾動，進而影響整個系統的穩定，因此如何抑制離軌過程中的系繩擺動是拖拽離軌任務的一個關鍵問題。目前已有一些相關的理論研究但還不廣泛。文獻[6]進行了圓軌道上繩系系統捕捉目標的動力學研究。文獻[7]進一步進行了雙繩系系統進行碎片主動移除的動力學研究。基于直接算法的最優控制理論被廣泛應用于系繩回收控制領域，直接算法以其通用性能夠很好地實現非線性動力學過程控制而避免對動力學本身的討論。在這一領域，Williams[8]、Wen等[9]的研究具有代表性。文獻[10]研究得到繩系系統星體姿態擺動將激發系統高階擺動并影響繩系系統的穩定，文獻[11]對此提出保持系數張力下抑制廢星姿態擺動的控制方法并且文獻[12]對此方法進行了進一步研究。

繩系系統的運動學具有強非線性，而且拖拽離軌過程中存在許多約束。故而需要在考慮這些約束因素下設計合適的控制律抑制拖拽離軌過程中系繩擺動。從20世紀70年代開始，針對具有復雜約束優化需求的控制問題，多年來大量工業實際中的成功應用表現出預測控制在解決這類問題的優勢[13-15]。本文針對霍曼變軌推力段的繩系系統系繩擺振抑制問題，建立了軌道平面內繩系系統動力學模型；以最優化結果為參考軌跡、非線性模型預測控制方法為基礎設計繩系系統拖拽離軌過程系繩平穩控制律，并通過仿真驗證了控制方法的跟蹤能力。

1 繩系系統動力學建模

1.1 建模假設和坐標系定義

為突出關鍵問題，做如下假設，主要考慮系繩和主星的面內姿態運動，即假設主星的滾轉角、偏航角，以及系繩的面外擺角為小角度，目標視為質點；不考慮系繩的彈性和質量；忽略除重力外的其余空間干擾力，主動力僅考慮推力，作用于主星質心；忽略除重力梯度力矩外干擾力矩，控制力矩作用于主星。

首先建立軌道坐標系So，zo軸沿地心連線方向由地球指向繩系衛星系統(TSS)質心，xo軸位于TSS質心軌道平面內與zo軸垂直并指向軌道運動方向，yo軸遵循右手準則，三軸單位矢量依次為eox、eoy和eoz。另外定義TSS本體坐標系Sb，zb軸沿著系繩指向主星，xb軸垂直系繩且在軌道平面內，三軸單位矢量依次為ebx、eby和ebz。為描述主星姿態運動，定義主星本體坐標系Sb1(三軸單位矢量依次為eb1x、eb1y和eb1z)，記Sb1相對軌道坐標系So的滾動、俯仰和偏航角分別為φ1、θ1、ψ1(3—1—2旋轉順序)。繩系系統坐標系如圖1所示。

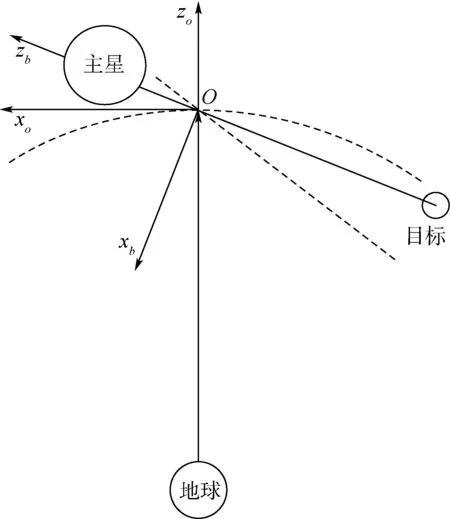
圖1 繩系系統坐標系示意圖Fig.1 Schematic of coordinate system of tethered system

1.2 簡化動力學方程

利用上述假設，整個主星拖拽系統可以由包含系繩長度、系繩面內外擺角和主星姿態角，將動力學方程線性化，消去高階項可以得到系統的動力學方程[16]。為簡化研究，忽略系統面外運動，本文研究霍曼變軌的第一次推力過程，主星初始位于同步軌道，變軌目標為墳墓軌道，因此系統運行的橢圓軌道偏心率很小，可以認為是圓軌道。在偏置耦合力當中引入上述假設，并忽略包括二階導數在內的高階小量。

簡化繩系系統的動力學方程式為[17]

(1)

(2)

(d1zsin(θ1-φ)+d1xcos(θ1-φ))Fte+T1y

(3)

式中：φ為系繩面內擺角(軌道坐標系So繞其y軸旋轉φ得到TSS本體坐標系Sb)；I1x、I1y和I1z為主星三軸慣量；T1y為主星y軸控制力矩大小；Fte為系繩張力；m1和m2分別為主星、子星的質量；m為系統總質量；l為系繩原長；ωo為軌道角速度；d1x、d1z分別為主星上x、z方向上的繩系點偏置大小；Fp為主星發動機推力大小；αp為主星發動機推力相對于軌道運動方向的夾角。動力學方程式(1)～式(3)形式較為簡單，利用了小角度假設，因此僅供穩定控制器設計所用。

為處理方便，采用的無量綱時間和無量綱長度分別為

(4)

式中：lt為單位繩長，可取為變軌前的TSS繩長。

做如下定義:

(5)

則可將式(5)轉化為狀態空間形式的系統動力學方程，x′=f(x,u)展開如下:

(6)

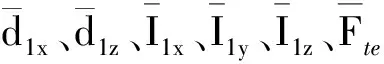
(7)

2 基于最優化求參考軌跡

參考軌跡采用最優化的方法求得。最優化方法一般描述為：尋找狀態和控制，使得性能指標達到最小，同時滿足包括系統狀態方程，一系列始末約束和過程約束在內的所有約束條件。下面針對由主星俯仰運動和系繩面內擺振組成的主星系統面內運動，具體分析應采用的性能指標和應滿足的約束條件，以建立最優問題。

2.1 性能函數選取

希望在最短的時間內完成所需的脈沖，因此將問題視為時間最短的最優問題，其性能函數為

(8)

2.2 控制約束

1) 始末約束

在開始變軌推力之前，繩系系統初值為

(9)

式中：φ0為系繩面內擺角初值，π/2-φmax≤φ0≤π/2+φmax，φmax為系繩面內擺角所允許的最大幅值。

變軌推力結束之后，繩系系統回到水平狀態，且繩長變化在可接受的范圍內，終值狀態如下：

(10)

式中：Λmin為出于防碰撞安全考慮所定義的最短無量綱繩長；Λmax為硬件所限最大的無量綱繩長。

2) 過程約束

系統的狀態變量應滿足系統動力學方程。對于控制量實際上也必然是有一個限度的。對控制量的約束這里主要考慮主星發動機推力方向φp的約束。

為了保證安全性，約束如下：

系繩面內擺角π/2-φmax≤φ≤π/2+φmax；主星俯仰角π/2-θ1max≤θ1≤π/2+θ1max；主星發動機推力方向αp,min≤αp≤αp,max；優化過程中對其他工程中重要性更低的量不做約束。其中φmax為系繩面內擺角所允許的最大幅值；?1max為主星俯仰運動所允許的最大幅值；αp,min為主星發動機推力方向所能達到的最小值，αp,max為主星發動機推力方向所能達到的最大值。

最后，整個推力段為避免系繩松弛，系繩的張力為非負。

(11)

3) 時間約束

顯然推力時間不可能是不受限的，最短時間應為推力方向一直維持軌道速度方向時，達到所需速度增量的時間，其表達式為

(12)

式中：ΔVp1為主星霍曼變軌第一段所需速度增量，其表達式為

(13)

其中：r1和r2分別為變軌前后的軌道半徑。

最大時間可人為設定，無量綱化即有

(14)

4) 推力約束

假定推力時間相對軌道周期而言很小(這個假設在同步軌道是成立的)，有限推力段在整個變軌過程中可以等效為脈沖推力，則推力提供的沖量在軌道方向應提供霍曼變軌所計算的速度增量，而在垂直軌道方向為0，即

(15)

(16)

至此，系統面內運動的最優控制問題已經建立：尋找滿足控制約束的狀態和控制集合，使得如式(8)所示的性能指標最小。

2.3 最優問題求解

本研究采用Legendre-Gauss-Lobatto(LGL)偽譜法，直接LGL偽譜法是目前應用最廣的偽譜方法之一[18]，具有較高的收斂速度并且能方便地處理高階導數，本文僅將此方法作為求解參考軌跡的方法，優化方法本身不是本文的重點。通過偽譜法將問題化為一個帶約束的非線性規劃問題，有成熟的尋優方法可以利用，本文采用MATLAB軟件自嵌的函數fmincon進行求解。通過求解這個最優控制問題得到參考軌跡。

3 基于非線性模型預測控制律設計

3.1 模型離散化

為了設計控制器，首先要將連續時間系統模型轉化為離散時間系統。將第1節得到的非線性連續時間系統x′=f(x,u)在(x(t),u(t-1))處線性化得到如下線性時變系統[19]：

Bt(u(t)-ur(t))

(17)

式中：xr(t)為參考狀態；ur(t)為參考控制量，由第1節給出;At和Bt的計算公式如下：

(18)

設定系統的采樣周期為T，得到離散化系統如下[20]：

x(k+1)=fd(x(k),u(k))=

Ad,tx(k)+Bd,tu(k)+dd,t

(19)

式中：

(20)

dd,t=xr(k+1)-Ad,txr(k)-Bd,tur(k)

(21)

其中：I為單位向量。

3.2 性能函數選取

模型預測控制的目標就是跟蹤期望的主星的三軸姿態和系繩擺角，即跟蹤參考軌跡。在離軌拖拽過程中，對于給定的主星參考姿態及系繩參考擺角，使得在空間拖拽過程中，主星姿態和系繩擺角的模型預測控制下的軌跡與最優化得到的參考軌跡相同。因此以主星姿態和系繩擺角速度跟蹤誤差、控制力矩和終端誤差作為優化目標，建立性能函數如下[15]：

e(Np)TPe(Np)

(22)

式中：e(k)為跟蹤誤差；Q、R和P為相應的跟蹤誤差、控制量和終端加權矩陣；Np和Nu分別為預測和控制時域。

3.3 主星姿態和系繩擺角的預測

利用繩系系統當前時刻k的信息x(k)，包括主星姿態、系繩繩長和繩長變化，得到k時刻非線性離散狀態空間模型如下[20]：

(23)

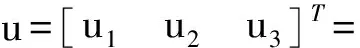
設定預測時域為Np，則可以根據繩系系統的當前狀態信息，利用離散化的繩系系統動力學及運動學方程，經過迭代計算，得到預測時域Np內的繩系系統狀態信息：

(24)

式中：x(k|k)=x(k)；y(k+i|k)為k時刻對未來k+i時刻系統輸出y(k+i)的預測值；u(k+i|k)為k時刻計算k+i時刻作用于系統的控制量。

因此得到預測時域Np內的控制量{u(k),u(k+1),…,u(k+Np-1)}。同時假設在區間[Np，Nu]內控制量保持不變，則可以得到

u(k+Nu-1)=u(k+Nu)=…=

u(k+Np-1)

(25)

因此利用繩系系統狀態模型和系統過去的控制量或輸出量，通過以上迭代計算出系統Np步預測輸出為

y(k)=(y(k+1|k),y(k+2|k),…,

y(k+Np|k))

(26)

3.4 控制約束

1) 始末約束

在開始變軌推力之前，繩系系統處于水平狀態，變軌推力結束之后，繩系系統回到水平狀態，這里約束和求解最優問題中的相同。

2) 過程約束

系統的狀態變量應滿足系統動力學方程。

模型預測控制過程約束包含跟蹤誤差的約束，對于狀態過程跟蹤誤差約束如下：

系繩面內擺角跟蹤誤差-Δφmax≤Δφ≤Δφmax；主星俯仰運動跟蹤誤差-Δθ1max≤Δθ1≤Δθ1max。

優化過程中對其他工程中重要性更低的量不做約束。其中Δφmax為系繩面內擺角跟蹤誤差所允許的最大幅值；Δθ1max為主星俯仰運動跟蹤誤差所允許的最大幅值。

系繩張力約束與最優問題中約束相同。

3) 推力約束

這里約束和求解最優問題中的相同。

3.5 非線性模型預測控制律實現

為了方便運算，將跟蹤誤差加權矩陣、控制力矩加權矩陣和終端加權矩陣設計為單位矩陣。并由式(19)和以上步驟可以形成如下滿足目標所要求的約束條件的繩系系繩擺振抑制控制的優化問題[15]。

(27)

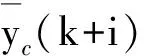
同樣通過偽譜法將問題化為一個帶約束的非線性規劃問題，并采用MATLAB軟件自嵌的函數fmincon進行求解。

4 基于非線性模型預測控制方法仿真驗證

取仿真參數如下：主星初始俯仰角為90°(90°為水平)，俯仰角速度為0；系繩初始擺角85°(90°為水平)，初始擺角速度為0。且繩系系統參數如表1所示。

設定拖拽約束要求如下：最短繩長10 m，最大繩長1 000 m；主星的姿態角擺動幅度不大于2°，姿態角速度不大于0.2 (°)/s；系繩擺動幅度不大于5 (°)/s，擺動角速度不大于0.2 (°)/s。主星推力方向最小值-π/4，主星推力方向最大值π/4。

設定模型預測控制誤差約束：系繩面內擺角跟蹤誤差所允許的最大幅值0.1°；主星俯仰運動跟蹤誤差所允許的最大幅值0.1°。

通過最優化方法求的最優軌跡即參考軌跡如圖2所示。使用模型預測控制得到的跟蹤路徑和最優化得到的參考軌跡的對比，如圖3所示。

從圖2中不難發現：采用最優化方法得到的參考軌跡能使實際離軌拖拽繩系系統回到水平位置，并使系繩面內擺角和主星俯仰角滿足約束要求，且系繩出于緊繃狀態。而且過程比較平滑。說明最優化得到的參考軌跡是可用的。

從圖3中可以看到：模型預測控制下的跟蹤路徑的各狀態很好地跟蹤了最優路徑即最優化得到的參考路徑。并且繩系系統的狀態控制在了約束范圍內，即系繩面內擺角和主星俯仰角滿足約束要求且系繩出于緊繃狀態。而且明顯可以通過縮小誤差約束范圍來提高跟蹤效果，但這樣又勢必提高計算量。又能從圖3看到，模型預測控制下的除了系繩面內擺角速度外，其他跟蹤路徑比較平滑，但系繩面內擺角速度抖動比較厲害，不夠平滑，如工程需要，須在跟蹤控制中對擺角速度誤差適當約束。模型預測算法具有在線優化的特點，魯棒性較好，但是其計算量較大的問題需要在今后進一步研究。

表1 繩系系統參數

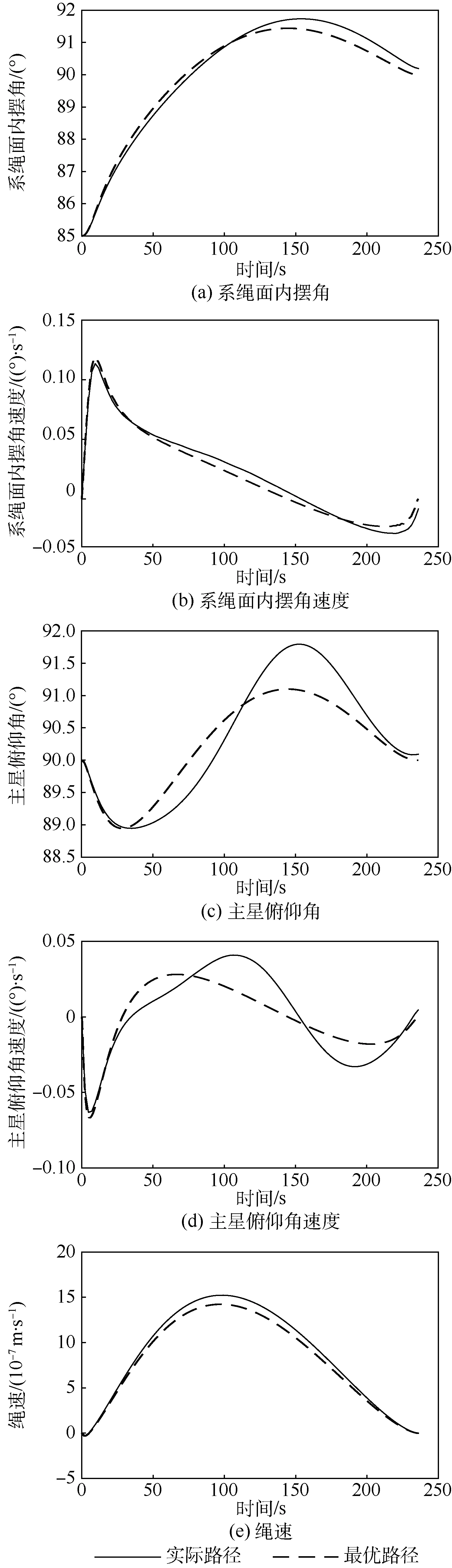
圖2 系繩面內擺角、系繩面內擺角速度、主星俯仰角、主星俯仰角速度和繩速的實際路徑和最優路徑Fig.2 Actual path and optimal path of tether’s in-plane swing angle, tether’s in-plane swing angular velocity, main satellite pitching angle, main satellite pitching angular velocity and tether speed

圖3 系繩面內擺角、系繩面內擺角速度、主星俯仰角、主星俯仰角速度和繩速的跟蹤路徑和最優路徑Fig.3 Tracking path and optimal path of tether’s in-plane swing angle, tether’s in-plane swing angular velocity, main satellite pitching angle, main satellite pitching angular velocity and tether speed

5 結 論

1) 考慮主星姿態、系繩擺角穩定、系繩張力為正、系繩長度變化有限等約束，針對繩系系統拖拽離軌推力作用過程中系繩擺振的抑制問題，進行系統狀態的最優軌跡求解，最優軌跡在滿足變軌速度增量要求的同時實現了推力時間最短。

2) 仿真結果表明，所設計的非線性模型預測控制方法很好地跟蹤了最優軌跡，并且滿足控制約束條件；在變軌推力作用下主星姿態和系繩擺動穩定，且動態過程平滑。