多無人機輔助定位信標的區域導航定位算法

許建新，熊智，陳明星，劉建業

南京航空航天大學 自動化學院，南京 210016

目前以GPS、北斗為代表的衛星導航系統已成為無處不在的定位、導航和授時信息源，是現代軍民通用的重要信息基礎設施，但是由于衛星導航系統自身固有的局限性，如信號功率低，易被敵方壓制或欺騙，在高對抗的作戰環境下的應用難以保障等，限制了其在一些特定條件和環境下的應用[1-2]。因此，為解決衛星導航系統的固有缺陷帶來的導航定位問題，世界各國都在積極發展衛星導航增強技術和區域導航系統[3]。為提高GPS抗干擾能力，美國國防高級研究計劃局最早提出了全球定位實驗偽衛星概念，并于2001年開始實施GPX計劃，演示了空基偽衛星概念的可用性。日本也提出平流層偽衛星飛艇輔助導航和定位的概念，將偽衛星置于高空平臺，擴大系統覆蓋范圍，將其應用于環境監測及通信等領域。澳大利亞的Locata公司發布了Locata系統，利用多個發射強無線電定位信號的地基偽衛星發射器組成的網絡實現定位，是采用類GPS定位技術的地基局域網絡[4-5]。

在利用偽衛星進行輔助定位過程中，需要確定偽衛星基站的位置及與用戶的距離，通過幾何定位解算出用戶位置[6-7]。為了更加快速靈活地部署偽衛星基站，實現無衛星環境下的區域導航定位功能，本文以無人機(UAV)作為空基平臺，提出一種區域導航定位算法，實現對地面用戶的定位。將無人機部署在預定空域，并播發自身位置及時鐘信息，地面用戶通過接收無人機位置及與無人機的距離，分別采用列文伯格-馬夸爾特(LM)算法模型和兩步最小二乘算法模型計算出地面用戶的實時位置，在衛星導航系統不可用情況下，滿足一定區域范圍內用戶的導航定位需求。

1 無人機輔助區域導航定位方案

(1)

以地面戰車為例，本文設計了基于無人機輔助的地面用戶導航定位方案。在圖1的區域導航定位場景中，在沒有GNSS信號的情況下，無人機編隊處于獨立組網模式，以其中一架無人機作為時間基準，其他無人機通過時間同步鏈路與基準無人機實現高精度時間同步[8-9]。考慮到無人機本身的定位誤差及測距誤差，直接采用式(1)求解可能會出現無解或虛數解的情況。

圖1 無人機輔助的地面用戶定位示意圖Fig.1 Sketch map of regional navigation based on unmanned aerial vehicles

為了綜合利用多架無人機的定位信息，本文采用LM非線性優化算法來求解地面用戶位置。LM算法能通過修改參數達到結合高斯-牛頓算法以及梯度下降法的優點，并對兩者的不足作改善，如高斯-牛頓算法中逆矩陣不存在時將無法繼續迭代的問題[10]。此外，為提高一般最小二乘算法的計算精度，消除地面戰車接收機與無人機之間的時鐘誤差，提出了兩步最小二乘算法，通過距離差分，消除鐘差，提高定位精度。在獲得地面戰車位置后，利用車載的慣性傳感器輸出信息，通過卡爾曼濾波算法進行數據融合，得到最終的導航結果輸出。具體方案圖如圖2所示。

圖2 基于無人機輔助的地面用戶定位方案Fig.2 Scheme of regional navigation based on unmanned aerial vehicles

2 無人機輔助的地面用戶定位算法模型

2.1 LM算法模型

在圖1的定位場景中，對地面用戶接收到的N架無人機信息，考慮到地面用戶的等效時鐘誤差εU，有

(2)

(3)

式中：AU為衛星導航偽距單點定位算法中的一個計算矩陣；

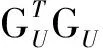
令

fi(Υ)=(xU-xi)2+(yU-yi)2+

(zU-zi)2-(Li-εU)2

式中：i=1,2,…,N，則用戶的坐標位置U的最優解U0等價為求解

(4)

根據泰勒公式將f(Υ)在Υ=Υk處展開，忽略二階小項，可得

f(Υ)≈f(Υk) +Ak(Υ-Υk)

(5)

式中：

f(Υ)的雅克比矩陣。

則

Q(Υ)≈(f(Υk) +Ak(Υ-Υk))T(f(Υk) +

Ak(Υ-Υk))

(6)

在傳統的高斯-牛頓迭代算法中，用戶位置及時鐘等效誤差的遞推公式為

(7)

(8)

(9)

在式(9)中，γk過大則會影響Υk+1的收斂速度，可以通過對比Q(Υk+1)和Q(Υk)的值進行動態調整。

2.2 兩步最小二乘算法模型

傳統最小二乘算法中，根據式(2)，第2～N個方程均減去第一個方程，整理后可得

HsΥ=bs

(10)

式中：

則，通過最小二乘計算可得

(11)

該算法簡單易實現，但是由于沒有考慮無人機的位置誤差和測距誤差，使得計算的定位結果誤差較大。針對圖1的定位場景，考慮到地面用戶與無人機的鐘差問題，并綜合利用無人機的位置誤差和測距誤差統計值，提出了兩步最小二乘算法，用于計算地面用戶的位置信息，其算法模型如下。

(12)

2(Uo-Si)TΔSi+2(Uo-S1)TΔS1

(13)

(14)

因此，式(13)可改寫為

(15)

(16)

(17)

式中：

(18)

(19)

(20)

cov(θ)=E(Δφ1(1:4)Δφ1(1:4)T)=

(GT(BQLBT)-1G-

GT(BQLBT)-1DR-1DT(BQLBT)-1G)-1

(21)

(22)

(23)

式中：Δθ(1∶3)為θ(1∶3)的估計誤差。

在式(23)中，兩端同時減去S1，再對向量中每個元素平方，略去二階小量，可得

-2(Uo-S1)⊙Δθ(1∶3)=

(Uo-S1)⊙(Uo-S1)

(24)

式中：⊙表示向量中對應元素的乘積。

(25)

將式(24)和式(25)合并寫成矩陣形式，得

(26)

式中：

根據最小二乘準則，可得地面用戶的位置結果為

(27)

由此可得地面用戶的定位結果表達式為

(28)

該算法第1步先求出地面用戶的誤差粗值，并求出其協方差矩陣，第2步利用誤差粗值的協方差矩陣及無人機的位置信息，計算出用戶與參考無人機的位置坐標差值，最終獲得地面用戶的位置估計結果。該算法綜合利用了無人機的位置誤差和測距誤差統計值，使得最終的計算結果相比一般最小二乘算法更為準確。

2.3 組合導航算法模型

以地面戰車為例，在采用以上方法計算出其位置之后，可以結合自身裝備的慣性導航系統輸出的傳感器信息進行組合導航，獲得連續可靠的定位。

2.3.1 系統狀態方程

在慣性導航系統中，選取18維系統誤差狀態量為[12]

X=

導航坐標系選取為東北天坐標系，可以獲得慣性導航系統的誤差狀態方程為

Xk=Φk|k-1Xk-1+Gk-1Wk-1

(29)

式中：Φk|k-1為慣性導航系統誤差方程所對應的狀態轉移矩陣；Gk-1為慣性導航系統誤差方程所對應的白噪聲誤差系數矩陣；Wk-1為慣性導航系統誤差方程所對應的白噪聲隨機誤差向量。

2.3.2 系統量測方程

在2.1和2.2節中，采用LM算法和兩步最小二乘算法計算出的地面用戶位置信息均為經度、緯度和高度。因此，在東北天導航坐標系下，2種 算法的量測模型相同，如式(30)所示。

ZM=HMX+VM=

(30)

式中：ZM為k時刻獲得的量測信息；HM為k時刻的量測系數矩陣；VM為k時刻的量測噪聲；wM1、wM2和wM3分別為緯度、經度和高度方向的定位誤差。

根據以上所推導的系統狀態方程和量測方程，設計對應的閉環卡爾曼濾波器為[13]

(31)

3 算法仿真驗證與分析

為驗證所提定位算法的有效性，首先采用Monte-Carlo方法進行靜態仿真，測試LM算法和兩步最小二乘算法的定位精度，然后再與地面戰車中的慣性導航定位算法進行組合導航仿真。

3.1 靜態測試

對無人機的空間分布已有學者進行了研究，本文假設有6架無人機，按照蜂窩型空間布局[14-15]，地面用戶靜止，仿真參數如表1所示，采用本文所提算法進行10 000次Monte-Carlo仿真。圖3為無人機和地面用戶的空間分布圖。

圖4～圖6分別為LM算法、一般最小二乘算法和兩步最小二乘算法的定位誤差分布。從圖中可以看出地面用戶的經度、緯度和高度的誤差分布皆近似服從正態分布，并且經度和緯度方向誤差較小，高度方向誤差較大。根據以上仿真結果分別統計了經度、緯度、高度3個方向的均值和標準差，如表2所示。

從表2的統計數據可以看出，LM算法和兩步最小二乘算法在水平方向定位誤差為10～13 m，2種算法的誤差標準差相近，但LM算法的誤差均值更小，在高度方向LM算法定位誤差標準差為334.5 m，兩步最小二乘算法誤差標準差為290.7 m，兩步最小二乘算法誤差更小，從三維分布誤差來看，兩步最小二乘算法略優。此外，從表中標準差數據可以得到，相比一般最小二乘算法，本文所提出的LM算法在經度、緯度和高度方向誤差分別降低了79.1%、63.2%和11.7%，兩步最小二乘算法在經度、緯度和高度方向誤差分別降低了78.9%、65.8%和23.2%，在精度上有較大提升。

表1 靜態環境下仿真參數設置Table 1 Simulation parameters setting in static condition

圖3 無人機和地面戰車的空間分布Fig.3 Space distribution of UAVs and terrestrial user

圖4 LM算法定位誤差Fig.4 Position error using LM algorithm

圖6 兩步最小二乘算法定位誤差Fig.6 Position error using two-step least square algorithm

AlgorithmParameterLongitude error/mLatitude error/mAltitude error/m3-D error/mConventional least square algorithmLM algorithmTwo-step least square al-gorithmMean value-0.76 0.195.265.32Standard deviation 61.39 30.42378.7384.85Mean value-0.19-0.295.175.18Standard deviation 12.85 11.19334.5334.93Mean value3.21 2.770.374.26Standard deviation 12.96 10.39290.7291.17

3.2 動態測試

在實際應用中，無人機和地面用戶每時每刻都處于運動狀態。本文設計了6架無人機及地面戰車的運動航跡，并通過提出的算法利用無人機位置信息和距離信息實時求解地面用戶的位置，再結合地面戰車本身的慣性導航系統獲得連續的位置輸出。圖7為無人機和地面戰車的三維航跡圖，在0～2 000 s，無人機起飛飛到預定區域，并在上空盤旋，在第2 000 s地面戰車開始運動，初始位置為109.75 °E，19.5 °N，高度為500 m。整個仿真時長為3 600 s。

圖8中紅色為一般最小二乘算法的定位誤差曲線，藍色為LM算法的定位誤差曲線，綠色為兩步最小二乘算法的定位誤差曲線。從圖中可以看出地面用戶的定位誤差呈現一定的周期性變化，這是由于無人機在空中盤旋使得幾何構型改變，從而引起定位誤差的變化。表3為動態情況下地面戰車的定位誤差統計，可以看出在地面戰車的運動過程中本文所提出的2種定位方法的標準差相近，但LM算法的高度方向精度稍差。

圖7 地面用戶和無人機的三維航跡圖Fig.7 Three dimensional trajectory of terrestrial user and UAVs

圖8 無人機輔助定位誤差Fig.8 Position error based on unmanned aerial vehicles

AlgorithmParameterLongitude error/mLatitude error/mAltitude error/m3-D error/mConventional least square algorithmLM algorithmTwo-step least square algorithmMean value-2.531.71-19.2919.53Standard deviation 44.1738.33 476.2479.8Mean value-0.310.44 2.542.60Standard deviation 17.118.91 330.1331.1Mean value 0.431.07-6.806.89Standard deviation 17.9318.81 297.2298.3

下面測試地面戰車組合導航結果。地面戰車的慣性導航系統參數配置如表4所示。

根據表3地面戰車定位誤差統計，將卡爾曼濾波算法中的量測噪聲經度、緯度和高度方向分別設置為20、20、300 m。

圖9和圖10分別為一般最小二乘算法、LM算法和兩步最小二乘算法下地面戰車組合導航的速度誤差和位置誤差曲線。表5對地面戰車組合導航的速度誤差和位置誤差進行了統計。從以上誤差對比結果可以看出，在與地面車輛慣性導航系統輸出進行卡爾曼濾波數據融合后，導航輸出結果更加穩定，本文提出的2種算法的誤差標準差相近。在高度方向，2種定位算法誤差均較大，可以考慮采用氣壓計等高度傳感器輔助，用以提高定位精度。

表4 地面用戶捷聯慣性導航系統參數配置

圖9 組合導航速度誤差曲線Fig.9 Velocity error curve of integrated navigation

圖10 組合導航位置誤差曲線Fig.10 Position error curve of integrated navigation

ParametersConventional least square algorithmLM algorithmTwo-step least square algorithmMean valueStandard deviationMean valueStandard deviationMean valueStandard deviationEast velocity error/(m·s-1)-0.330.93-0.290.72-0.250.75North velocity error/(m·s-1) 0.470.99-0.060.71 0.390.71Up velocity error/(m·s-1)-1.122.50 1.032.17-0.202.16Longitude error/m-5.2115.12-2.567.53-1.498.23Latitude error/m 5.7713.79 0.768.27 4.338.00Altitude error/m-28.37106.8 25.8579.01-8.7568.09

4 結 論

1) 針對衛星導航系統受到干擾不可用的情況，利用無人機的位置及其與用戶的距離信息，分別采用LM算法模型和兩步最小二乘算法模型計算出地面用戶的實時位置，解決了偽距定位算法中矩陣不可逆問題，從定位結果來看，本文所提出的算法相比一般最小二乘算法在精度有較大提升。

2) 結合地面用戶自身的慣性導航系統，通過卡爾曼濾波算法進行信息融合，獲得地面用戶連續的位置信息。仿真驗證表明，采用本文所提出的區域導航定位算法，可以在衛星導航系統拒止環境下，滿足一定區域范圍內用戶的導航定位需求。

3) 從靜態定位精度結果來看，LM算法和兩步最小二乘算法均能實現對地面用戶的定位，從三維空間誤差統計來看，兩步最小二乘算法精度略優。但由于2種算法的原理不同，無人機分布的幾何構型以及無人機本身定位精度和測距誤差等因素對這兩種算法的影響還需要再深入研究。