獨立泊松序列與指數(shù)序列的變點檢測方法比較

韓冰凌，孫佳楠

（北京林業(yè)大學 理學院，北京 100083）

0 引言

變點檢測涉及的基礎學科涵蓋了數(shù)理統(tǒng)計、應用數(shù)學、計算機科學等，并在金融學、經(jīng)濟學、氣象學、環(huán)境學等多個學科中廣泛應用。例如，在金融學研究中，宿成建和陳潔[1]應用變點模型研究了滬深股股市波動性突變行為，并分析了1992—2002年上證和深證綜合指數(shù)的方差變點，對這些變點的經(jīng)濟意義進行了解釋。在自然環(huán)境研究中，涂新軍和陳曉宏[2]基于變點原理，運用似然比方法研究了存在變點的河川徑流量序列，并給出了一系列的結論。

注意到對泊松分布序列和指數(shù)分布序列的變點檢測研究不多見，但其具有較強的實際應用價值。一些稀有事件如地震、煤礦災難等的發(fā)生近似服從泊松分布，總結這些稀有事件的發(fā)生規(guī)律及發(fā)展過程中的規(guī)律突變，對于防范自然災害等有重大意義，如對礦難發(fā)生次數(shù)的變點分析[3]、稀有事件變點問題的分析[4]等。一方面，產(chǎn)品的壽命以及隨機服務系統(tǒng)的服務時長等往往服從指數(shù)分布，檢測這些指數(shù)序列的變點，可以為提高生產(chǎn)質(zhì)量和改進服務質(zhì)量提供科學依據(jù)，如黃志堅和張志華[5]研究了可靠性數(shù)據(jù)在變點前后服從不同參數(shù)的指數(shù)分布產(chǎn)品的壽命分布，建立了產(chǎn)品故障分布的模型。

基于上述兩種分布的獨立序列數(shù)據(jù)，有必要通過模擬實驗就不同變點檢測方法的檢測效果進行比較研究，并給出能夠指導實際應用的有價值的參考建議。R軟件中的Changepoint程序包[6]是近年開發(fā)的簡單實用的變點檢測程序包，其中包含了經(jīng)典的僅一個變點（Atmost One Changepoint;AMOC）檢測法[6]和Binary Segmentation（BS）方法[7]，也包含了最近提出的Pruned Exact Linear Time（PELT）方法[8]。本文針對泊松和指數(shù)分布序列，使用該程序包下的上述三種變點檢測方法，分別對不同情境下的獨立泊松序列和指數(shù)序列進行均值方差變點的檢測和比較。

1 三種均值方差變點檢測方法

1.1 變點問題的提法

變點一般是指觀察序列中統(tǒng)計性質(zhì)發(fā)生變化的點的位置，統(tǒng)計學變點檢測問題是對該位置的估計問題。設一個按時間順序排列的觀察值序列記為 y1:n=(y1，...，yn)，若存在一個時間點τ∈{1，...，n-1}，使得這個時間點之前的序列{y1，...，yτ}和這個時間點之后的序列{yτ+1，...，yn}具有某方面不同的統(tǒng)計性質(zhì)，那么該時間點τ稱為一個變點。當這兩個子序列的均值參數(shù)變化，τ稱為均值變點；當這兩個子序列的均值和方差參數(shù)都變化，τ稱為均值方差變點。如果序列只存在一個變點，稱為單變點；如果變點數(shù)量為m，即存在不只一個變點，稱 τ1:m=(τ1，...，τm)為多變點[9]。

1.2 單變點問題

單變點檢測可以轉化為假設檢驗問題，原假設是觀察值序列無變點，備擇假設為存在一個變點。該檢驗問題可通過似然比檢驗實現(xiàn)，具體參見正態(tài)分布下均值單變點的檢測研究[10]和正態(tài)方差單變點的檢測研究[11]。

1.3 多變點問題

對于多變點問題，常將變點檢測問題轉換為目標函數(shù)的優(yōu)化問題其中，C為損失函數(shù)，可以采用負對數(shù)似然函數(shù)。βf(m)為懲罰函數(shù)，可以采用 AIC[12]、BIC[13]的懲罰形式。

具體地，使用BS方法[7]優(yōu)化上述目標函數(shù)的思想：第一步，在觀察值序列中只檢測一個變點的位置，如果序列中存在一個τ滿足 C(y1:τ)+C(y(τ+1):n)+β＜C(y1:n)，則認為發(fā)現(xiàn)了一個變點；第二步，針對yτ分得的兩個子序列，分別進行單變點檢測……直到每個子序列中不再檢測出變點。若第一步找不到單變點，則認為此序列沒有變點。BS方法是將單變點檢測的思路應用于多變點檢測問題，方法中常取 f(m)=m。BS方法具有運算效率高的優(yōu)點，但不能保證檢測出的變點是目標函數(shù)優(yōu)化的全局最優(yōu)解。

若使用PELT方法[8]優(yōu)化上述目標函數(shù)，則需以Optimal Partitioning(OP)算法為基礎。OP算法的思想是采用遞歸的方式優(yōu)化目標函數(shù)。記F(s)=min{F(t)+C(y(t+1):n) +β} ，其中，F(xiàn)(t)表示數(shù)據(jù) y1:t中函數(shù)最小值。OP算法沒有BS方法的求解效率高，于是PELT方法在OP算法的基礎上增加了一個剪枝[8]過程，通過剪枝操作來提高運算效率，剪枝的本質(zhì)是去掉每次迭代過程中不能起到減小F(t)作用的τ。

2 模擬研究

針對獨立泊松分布和指數(shù)分布序列中的變點檢測問題，分別應用AMOC、PELT、BS方法進行模擬實驗并比較其效果，從而給出觀察值序列服從兩種不同分布下的方法選擇建議。

2.1 研究設計

模擬數(shù)據(jù)分別來自獨立泊松分布和獨立指數(shù)分布。每種分布下分別設計觀察值序列的樣本量為1000、1500；當變點個數(shù)設計一個變點時，分布參數(shù)的變化范圍為由3變?yōu)?，或由2變?yōu)?.5；當變點個數(shù)為兩個時，分布參數(shù)的變化范圍為由3變?yōu)?再變?yōu)?，或由2變?yōu)?.5再變?yōu)?；故共8種情境。每種模擬情境生成5組數(shù)據(jù)來進行重復實驗。目標函數(shù)中分別采用AIC、BIC兩種信息準則作懲罰項。研究中使用R Changepoint程序包的不同變點檢測方法來檢測泊松和指數(shù)分布中的變點。泊松分布與指數(shù)分布有一個共同的特點：均值參數(shù)和方差參數(shù)同時變化。因此使用均值方差變點命令cpt.meanvar進行檢測。該程序包可以選擇檢測變點的懲罰項類型如AIC、BIC。

2.2 研究結果

模擬結果從以下角度分析：檢測的變點數(shù)、變點位置、輸出的負對數(shù)似然值的情況。影響結果的變量為觀察值序列的樣本量、變點個數(shù)、分布的參數(shù)、變點檢測方法的選取、懲罰函數(shù)類型。用N表示樣本個數(shù)，n表示變點個數(shù)，λ表示泊松或指數(shù)分布的參數(shù)。

2.2.1 泊松分布序列的變點檢測結果

在表1中，數(shù)字代表正確識別的變點數(shù)，“-”代表變點個數(shù)為2時不再使用AMOC方法。作為判定變點檢測效果的標準，此處著重考察每種方法得到的變點中，是否包含變點真值，即變點的準確位置。具體地，從檢測到的變點中，首先選出距離真實變點最近的位置，再判定其是否距離真實變點在三個時間點以內(nèi)；若是，則視為檢測正確。由表1看出：當變點數(shù)為一個時，使用三種方法正確檢測的變點數(shù)的均值相同，此時這三種方法沒有太大差異。當變點數(shù)為兩個時，PELT方法正確檢測的變點數(shù)平均而言多于BS方法。比較兩種懲罰類型，BIC懲罰下正確檢測的變點數(shù)平均而言多于AIC懲罰。

表1 不同方法正確檢測泊松分布序列變點的個數(shù)

由表2看出：從檢測到的變點個數(shù)看，不管選取的樣本量及參數(shù)如何變化，當真實情況存在一個變點時，顯然AMOC檢測的變點總數(shù)一定準確，而其他兩種方法的變點數(shù)在使用AIC類型的懲罰項時均大于一個，使用BIC類型的懲罰項時表現(xiàn)較好。若樣本量不同，其他條件相同，使用AIC懲罰項的PELT方法找出的變點數(shù)會隨著樣本量的增大而增大，而其他情況檢測出的變點數(shù)量與樣本量變化無關。當真實情況存在兩個變點時，顯然AMOC不再適用，使用AIC懲罰項的PELT方法找出的變點數(shù)會隨著樣本量的增大而增大。總體而言，針對懲罰類型選取的不同，BIC懲罰明顯優(yōu)于AIC懲罰下的變點識別效果。

表2 不同方法檢測的泊松分布序列的變點總數(shù)

再從負對數(shù)似然值的大小來看（由于篇幅所限，不展示負對數(shù)似然值的表格）：若檢測變點的方法選取不同（不再考慮AMOC方法），使用AIC懲罰下的PELT方法有時會出現(xiàn)NAN的情況。針對不同的懲罰類型進行比較，BIC懲罰下負對數(shù)似然值小于AIC懲罰下的負對數(shù)似然值。

2.2.2 指數(shù)分布序列的變點檢測結果

由表3，當變點數(shù)為一個時，使用三種檢測方法正確檢測變點的平均數(shù)相差不大，此時這三種方法沒有太大差異。PELT方法相比于另兩種方法正確檢測的變點數(shù)略多。當變點數(shù)為兩個時，比較BS方法和PELT方法，PELT方法正確檢測的變點數(shù)的均值與BS方法無明顯差異。BIC懲罰下正確檢測的變點數(shù)平均而言與AIC懲罰相似。

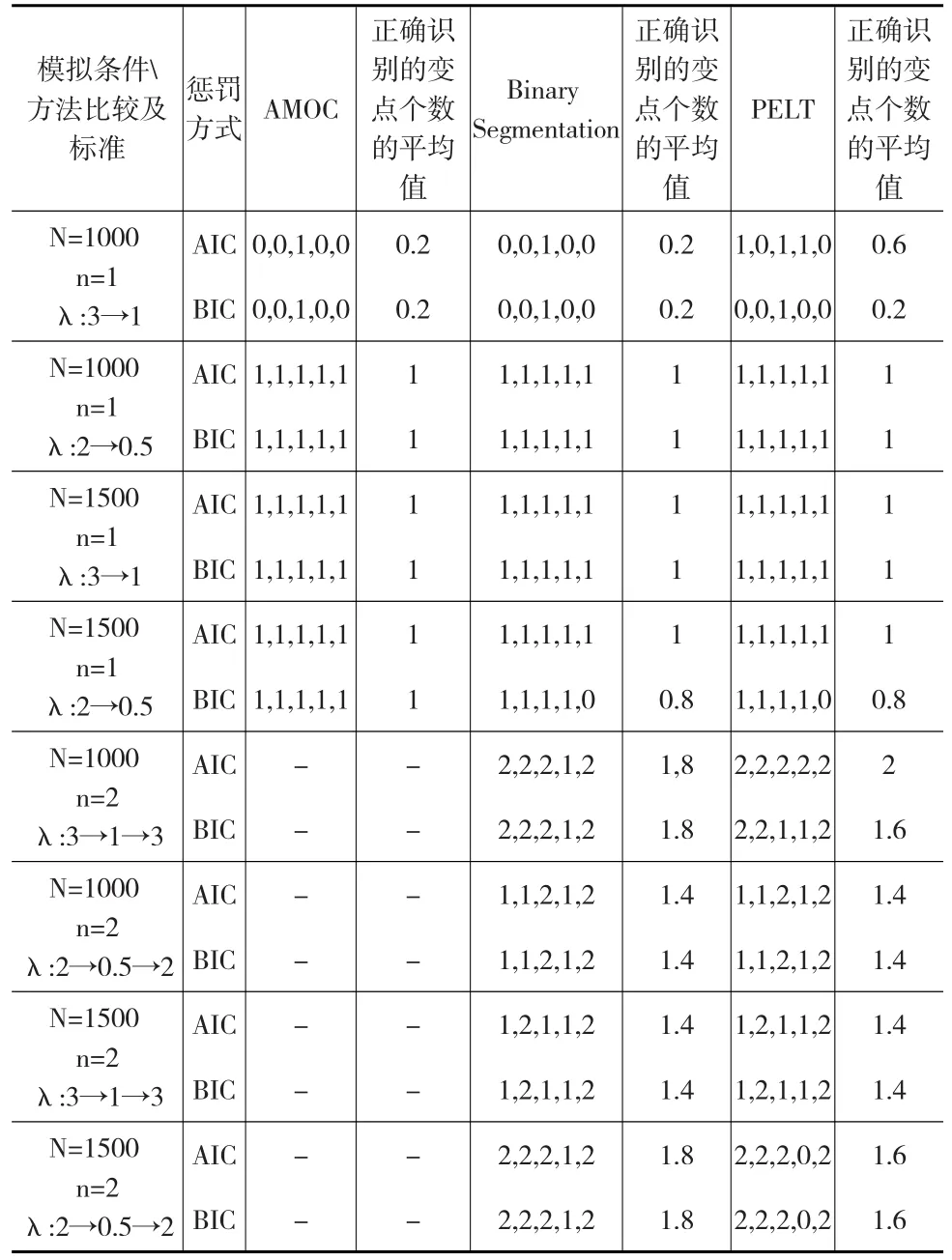
表3 不同方法正確檢測指數(shù)分布序列變點的個數(shù)

由表4看出，類似于泊松序列的研究結果，當真實情況存在一個變點時，顯然AMOC檢測的變點總數(shù)一定準確，而其他兩種方法的變點數(shù)在使用BIC懲罰項比AIC好。若樣本量不同，其他條件相同，使用AIC懲罰項的PELT方法找出的變點數(shù)會隨著樣本量的增大而增大，而其他情況檢測出的變點數(shù)量與樣本量變化無關。當真實情況存在兩個變點時，使用AIC懲罰項的PELT方法明顯比BS方法差，但適用BIC懲罰時二者表現(xiàn)相似。

從負對數(shù)似然值的大小來看（由于篇幅所限，不展示負對數(shù)似然值的表格），N=1500時的負對數(shù)似然值要大于N=1000時的負對數(shù)似然值；若懲罰類型選取不同，其他變量均相同，使用PELT方法時，BIC懲罰下負對數(shù)似然值小于AIC懲罰下的負對數(shù)似然值；若使用BS方法，兩種懲罰方式下負對數(shù)似然值相同。

表4 不同方法檢測的指數(shù)分布序列的變點總數(shù)

3 實證

Carlin等（1992）[3]針對1851—1962年這 112年間英國每年發(fā)生煤礦災難次數(shù)的數(shù)據(jù)，使用貝葉斯方法進行變點檢測并找到一個變點k=41，其對應年份為1891年；每年發(fā)生礦難的平均數(shù)由1891年之前的3.10下降到1891年之后的0.90。圖1為1852—1962年英國煤礦災難每年的發(fā)生次數(shù)時序圖。

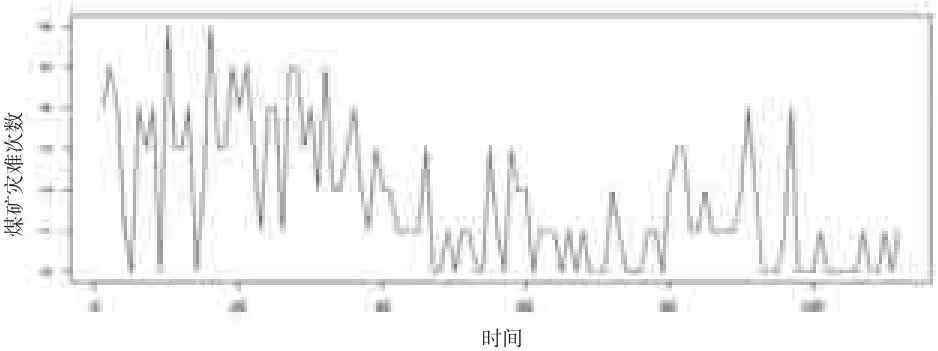
圖1 1851—1962年英國每年發(fā)生煤礦災難次數(shù)的時序圖

根據(jù)該數(shù)據(jù)的產(chǎn)生背景，不妨假設序列中各隨機變量相互獨立并服從泊松分布。這里分別使用AMOC、BS和PELT方法分析該數(shù)據(jù)，觀察不同檢測變點方法及懲罰方式檢測變點的效果，并與Carlin等（1992）的研究結果進行比較。由表5看出，AMOC方法可以較準確地檢測到變點。PELT方法采用AIC懲罰時過于敏感，檢測出的變點數(shù)較多；采用BIC懲罰時可以減輕這種情況。BS方法表現(xiàn)較好，適用BIC懲罰時比AIC懲罰表現(xiàn)更好。

表5 三種方法對英國礦難數(shù)據(jù)的變點檢測結果

進一步，如果對BS方法約束檢測到的變點個數(shù)為一個，BS方法檢測到的變點也是準確的，結果見下頁表6。

表6 約束BS方法僅檢測一個變點的結果

4 結論

本文的研究得到以下結論：首先，對模擬研究，當觀測值服從泊松分布且只有一個變點時，AMOC方法一定可以檢測到準確的變點數(shù)量和位置，并且此時具有較小的負對數(shù)似然值，因此相對其他兩種方法較優(yōu)。若使用另外兩種方法，最好選擇BIC懲罰類型，不論從檢測出的變點個數(shù)準確度或負對數(shù)似然值來看，使用BIC懲罰要優(yōu)于使用AIC懲罰。相對而言，BS方法要優(yōu)于PELT方法。當泊松序列中存在兩個變點時，比較BS方法與PELT方法，看出兩種方法均在BIC懲罰下可以得到較準確的變點數(shù)量和較小的負對數(shù)似然值。其次，指數(shù)分布的結果與泊松分布類似，當變點個數(shù)為一個時，使用AMOC方法可以檢測到準確的變點位置，并且此時具有較小的負對數(shù)似然值，相對其他兩種方法較優(yōu)。當變點數(shù)為兩個時，使用BS方法與BIC懲罰結合使用、PELT方法與BIC懲罰結合使用得到的結果是類似的。再有，通過對實證研究中的變點檢測并與前人研究結果對比，發(fā)現(xiàn)AMOC、BS、PELT三種檢測方法的檢測效果優(yōu)劣與模擬結果類似。總之，泊松序列或指數(shù)序列存在一個變點時，使用均值方差同時變化的AMOC方法相比另外兩種方法更優(yōu)；對存在兩個變點的情況，BS或PELT結合BIC懲罰均較好，前者略優(yōu)于后者。本文的結果對于泊松和指數(shù)分布序列如何選擇三種方法來檢測變點具有較好的指導意義，未來研究還可探索對隨機變量序列服從其他分布類型時上述三種方法的變點檢測效果的比較。