預(yù)折管的耐撞性分析和多目標(biāo)參數(shù)優(yōu)化

劉菲

摘 要：本文主要介紹兩種預(yù)折管，它與傳統(tǒng)薄壁管不同的是其管壁上有一些褶皺。文章首先介紹了兩種預(yù)折管的幾何結(jié)構(gòu)；然后建立預(yù)折管的有限元模型并驗(yàn)證有限元模型的正確性；其次對(duì)預(yù)折管的幾何參數(shù)進(jìn)行參數(shù)分析，發(fā)現(xiàn)b（兩相鄰菱形葉頂點(diǎn)間的長(zhǎng)度），l（兩相鄰菱形葉頂點(diǎn)間的寬度），t（管壁厚度）對(duì)結(jié)構(gòu)的吸能特性有著重要的影響；最后對(duì)預(yù)折管的幾何參數(shù)進(jìn)行了對(duì)多目標(biāo)優(yōu)化，優(yōu)化目標(biāo)是獲得最小的IPF和最大的比吸能（SEA），通過(guò)RBF代理模型和遺傳算法二代（NSGA-II）得到了優(yōu)化的Pareto解集。優(yōu)化結(jié)果顯示預(yù)折管具有更優(yōu)的耐撞性，可以作為一種潛在的吸能結(jié)構(gòu)。

關(guān)鍵詞：薄壁結(jié)構(gòu)；預(yù)折管；碰撞分析；參數(shù)設(shè)計(jì)

中圖分類(lèi)號(hào)：U461.91 文獻(xiàn)標(biāo)識(shí)碼：A 文章編號(hào)：1005-2550（2018）04-0014-11

Abstract： In this study， two different origami pattern tubes are introduced. Unlike existing traditional thin-walled structures， there are some folds around origami tubes' wall. Firstly， this paper introduce the structure of two origami tubes. Next the finite element model of origami tubes are established and validated by experiments. Then， a parameter study on origami tubes indicates that b （the length of two adjacent vertexes）， l （the width of two adjacent vertexes） and t （wall thickness） have significant influence on crashworthiness. Finally， the multiobjective optimization is carried out to obtain an optimized structural configuration for maximizing SEA and minimizing IPF. By adopting RBF surrogate model and NSGA-II，the Pareto optimal solutions are derived. The results show that origami tubes have superior crashworthiness and can be potential energy absorbers.

Key Words： Thin-walled structure； Origami tubes； Crashing analysis； parameter design

引 言

大量的薄壁金屬管因?yàn)槠涓咝У奈苣芰Α⒑?jiǎn)單的制造工藝以及低廉的成本而被廣泛的應(yīng)用在汽車(chē)的吸能結(jié)構(gòu)上[1，2]。在過(guò)去的幾年間，輕量化和耐撞性在汽車(chē)、航天、交通以及國(guó)防工業(yè)取得很多的關(guān)注。薄壁金屬管通過(guò)一種理想的塑形變形來(lái)吸收能量，這比通過(guò)結(jié)構(gòu)屈服而吸能要多很多。因此對(duì)薄壁結(jié)構(gòu)的研究吸引了很多學(xué)者的關(guān)注。

現(xiàn)代的白車(chē)身主要是由薄壁結(jié)構(gòu)所組成，這些薄壁大多數(shù)是由傳統(tǒng)的金屬板沖壓成型的。在國(guó)內(nèi)外有很多學(xué)者都對(duì)汽車(chē)上薄壁結(jié)構(gòu)進(jìn)行分析，以此來(lái)提高汽車(chē)的耐撞性和降低汽車(chē)的重量。其中文獻(xiàn)[3]首先提出了在準(zhǔn)靜態(tài)和動(dòng)態(tài)壓縮過(guò)程中，圓管和方管的平均壓潰力的數(shù)學(xué)表達(dá)式；文獻(xiàn)[4]將連續(xù)變截面板（TRB）應(yīng)用到汽車(chē)前縱梁上并進(jìn)行了仿真優(yōu)化。文獻(xiàn)[5]對(duì)不同截面幾何圖形的薄壁管進(jìn)行了吸能和變形的對(duì)比。文獻(xiàn)[6]也對(duì)國(guó)產(chǎn)某SUV進(jìn)行了B柱的輕量化優(yōu)化。盡管傳統(tǒng)薄壁管已經(jīng)展現(xiàn)出杰出的吸能特性以及輕重量，但是在碰撞過(guò)程中往往會(huì)產(chǎn)生較高的初始峰值壓潰力（IPF， Initial Peak Force）。過(guò)高的IPF會(huì)給乘員帶來(lái)嚴(yán)重的傷害甚至是死亡。而傳統(tǒng)的降低IPF的方法主要是將結(jié)構(gòu)設(shè)計(jì)成有幾何缺陷的，但這樣會(huì)導(dǎo)致整個(gè)吸能能力的降低。隨著研究的不斷深入，有的學(xué)者將連續(xù)變截面板應(yīng)用到薄壁構(gòu)建中。如文獻(xiàn)[7]提出一種連續(xù)變厚度的矩形管，在正面壓潰的過(guò)程中有著更低的IPF。另一些學(xué)者通過(guò)對(duì)薄壁結(jié)構(gòu)的管壁進(jìn)行適當(dāng)?shù)母倪M(jìn)，使其壓潰的變形形式控制在理想的模式下。眾所周知，對(duì)稱(chēng)式的屈服形式要比非對(duì)稱(chēng)式的屈服形式吸收更多的能量?；谶@個(gè)理論，文獻(xiàn)[8]提出兩種預(yù)折薄壁管，其在軸向壓潰過(guò)程中有著更小的IPF。本來(lái)就是在文獻(xiàn)[8]提出的預(yù)折薄壁管的基礎(chǔ)上，對(duì)其進(jìn)行有限元模型的建立，幾何參數(shù)參數(shù)分析和優(yōu)化。

1 兩種預(yù)折管的結(jié)構(gòu)

1.1 兩種預(yù)折管管的幾何結(jié)構(gòu)和材料模型

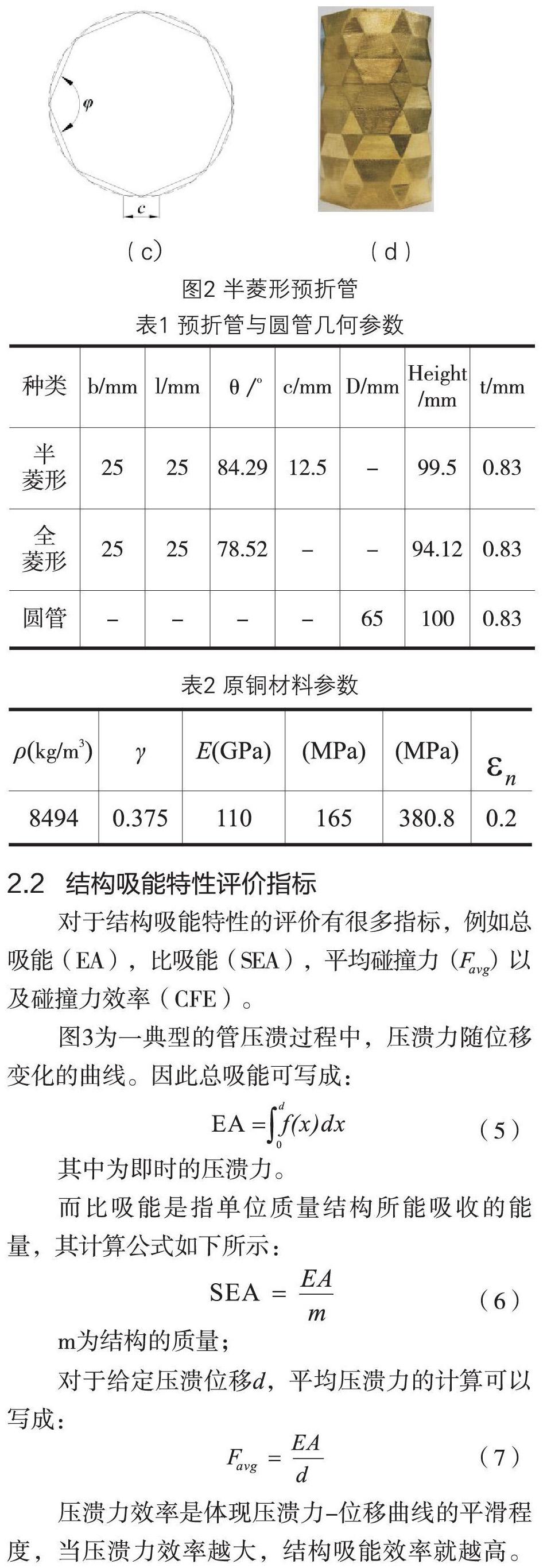
本文所分析的幾何模型是文獻(xiàn)[8]提出的2種截面為正8邊形的預(yù)折薄壁管，如圖1和圖2所示。這種預(yù)折薄壁管是由日本的折紙方法衍生而來(lái)的。圖1所示為全菱形預(yù)折管，圖1a中有一些實(shí)線和虛線，實(shí)線代表突出的部分，而虛線代表凹進(jìn)去的部分。通過(guò)將這個(gè)紙條按照實(shí)線和虛線折起來(lái)，然后將紙片的首尾兩端連接起來(lái)就可以形成如圖1b所形成的小樣本。而圖1c的實(shí)物圖形就是由圖1b鏡像而成。全菱形預(yù)折管中幾何參數(shù)θ表示一個(gè)菱形中，上下兩個(gè)三角形面的二面角；b代表兩個(gè)相鄰菱形葉頂點(diǎn)的長(zhǎng)度，而l代表一個(gè)菱形葉的長(zhǎng)度；α表示在同一菱形葉上折紙實(shí)線在水平面上的投影和虛線在水平面上投影的夾角。因?yàn)轭A(yù)折管的特殊結(jié)構(gòu)，其幾何參數(shù)有一下關(guān)系：

由公式（3）可以看出θ僅僅由b和l所決定，因此截面為正八邊形的全菱形預(yù)折管是不可以展開(kāi)的。預(yù)折管的這種不可展開(kāi)的特性使得其在壓潰過(guò)程比可展開(kāi)薄壁管吸收更多的能量[9]，因此全菱形預(yù)折管是一種更高效的吸能結(jié)構(gòu)結(jié)構(gòu)。對(duì)于半菱形預(yù)折管，其結(jié)構(gòu)與全菱形預(yù)折管相似，如圖2所示。半菱形預(yù)折管比全菱形預(yù)折管要多一個(gè)幾個(gè)參數(shù)c。如圖2a所示，c為一個(gè)菱形葉兩個(gè)頂點(diǎn)的寬度。對(duì)于半菱形預(yù)折管，其幾何參數(shù)滿足以下關(guān)系：

由公式（3）和公式（4）可以看出，其結(jié)構(gòu)非常相似，當(dāng)c=b時(shí)，半菱形預(yù)折管就變成了全菱形預(yù)折管。兩種預(yù)折管具有以下兩種特性：（1） 圖1b和圖2b可以看成是一個(gè)基本部件，本文的預(yù)折管就是由4個(gè)基本部件組成。（2）隨著二面θ的增加，碰撞吸能曲線會(huì)上移，這就意味著吸收更多的能量[10]。

為了對(duì)比預(yù)折管和普通圓管的吸能特性，具有相似參數(shù)的圓形管也被制造。這三種管的幾何參數(shù)如圖表1所示，其中D為圓管直徑，H為管子高度，t為薄壁管的厚度。

2.2 結(jié)構(gòu)吸能特性評(píng)價(jià)指標(biāo)

對(duì)于結(jié)構(gòu)吸能特性的評(píng)價(jià)有很多指標(biāo)，例如總吸能（EA），比吸能（SEA），平均碰撞力（ ）以及碰撞力效率（CFE）。

2 預(yù)折管有限元模型驗(yàn)證及參數(shù)分析

2.1 預(yù)折管有限元模型

本文主要采用顯式有限元求解器LS-DYNA 971用來(lái)模擬預(yù)折管的軸向壓潰。如圖4所示，預(yù)折管的有限元模型主要采用四節(jié)點(diǎn)的殼單元來(lái)模擬，其中每個(gè)點(diǎn)擁有6個(gè)自由度。殼單元的尺寸設(shè)置為1.5mm，殼單元在厚度方向上設(shè)置五個(gè)積分點(diǎn)以防止沙漏的出現(xiàn)。在有限元模型中，質(zhì)量塊和預(yù)折管之間的接觸設(shè)置成自動(dòng)的面-面接觸，動(dòng)靜摩擦因素都設(shè)置為0.25。預(yù)折管自身采用自動(dòng)自接觸，以防止其自身穿透，動(dòng)靜摩擦因數(shù)也為0.25。模型的材料為L(zhǎng)S-DYNA中的彈塑性材料（MAT24）。在軸向壓潰的仿真中，預(yù)折管下端節(jié)點(diǎn)約束其6個(gè)方向的自由度，上端與質(zhì)量塊之前存在一個(gè)0.5mm的間隙，以防止初始穿透。試驗(yàn)時(shí)，質(zhì)量塊以8 m/s壓縮預(yù)折管。為了減小試驗(yàn)中質(zhì)量塊下落時(shí)與預(yù)折管剛接觸時(shí)的應(yīng)力波動(dòng)很大，仿真時(shí)質(zhì)量塊的速度按照如圖所示從0變化到8m/s速度曲線加載。文獻(xiàn)[12]表明，按照這樣的速度曲線加載的結(jié)果和試驗(yàn)的質(zhì)量塊固定速度加載方式得到的結(jié)果吻合度很高。

2.2 有限元模型的驗(yàn)證

文獻(xiàn)[6]做了本文中預(yù)折管的壓潰試驗(yàn)來(lái)驗(yàn)證有限元模型的精確性。如圖6所示，ESA-CU200機(jī)器上放置了一個(gè)半菱形預(yù)折管，而試驗(yàn)樣本的預(yù)折管參數(shù)如表1所示，試驗(yàn)過(guò)程中，ESA-CU200機(jī)器上的質(zhì)量塊以8000mm/s的速度往下移動(dòng)，通過(guò)對(duì)比試驗(yàn)中預(yù)折管的變形（圖6b）與仿真中預(yù)折管的變形（圖6c），發(fā)現(xiàn)兩者基本一致，說(shuō)明有限元模型是準(zhǔn)確的。

圖7所示的為試驗(yàn)和仿真的壓潰力-位移曲線。試驗(yàn)和仿真的初始?jí)簼⒘Ψ逯捣謩e為16.21kN和18.38kN，兩者基本一致。從圖7可以看出，試驗(yàn)壓潰力-位移曲線略低于仿真壓潰力-仿真曲線，這是由于在試驗(yàn)中，預(yù)折管出現(xiàn)了明顯的撕裂，這直接導(dǎo)致其吸能曲線的下降，此外，材料的缺陷也是導(dǎo)致試驗(yàn)曲線略低一個(gè)重要影響因素。雖然試驗(yàn)曲線與仿真曲線有點(diǎn)差距，但是兩者的主要趨勢(shì)是一致的。通過(guò)預(yù)折管的變形圖、壓潰力-位移曲線可以得出，仿真和試驗(yàn)有著很高的一致性。因此有限元模型是精確可靠的。

3 預(yù)折管的耐撞性分析

3.1 兩種預(yù)折管和圓管在不同厚度時(shí)的吸能特性對(duì)比

本部分主要建立了12個(gè)有限元仿真模型來(lái)對(duì)比預(yù)折管和圓管在不同厚度t的吸能能力的對(duì)比。12個(gè)模型的幾何參數(shù)以及仿真結(jié)果圖表3所示。

如表3所示，其中D為圓管的直徑，而對(duì)于兩種預(yù)折管，D為其截面正八邊形的外接圓直徑。在初始峰值壓潰力（IPF）上，全菱形預(yù)折管1和半菱形預(yù)折管1分別為15.704kN和18.422kN，要比圓管分別低41.8%和31.9%；而在比吸能（SEA）方面，全菱形預(yù)折管1和半菱形預(yù)折管1和圓管分別為5.236kJ/kg、4.22kJ/kg和4.58kJ/kg，很顯然全菱形管具有更高的吸能效率。隨著厚度的增加三種管的吸能特性基本一致，例如圓管4，半菱形管4和全菱形管4的IPF分別為88.947kN，88.033kN和86.697kN，基本上沒(méi)有差距。而對(duì)與SEA，圓管4只比半菱形管低1%，比全菱形管高5%。此外，圖8表示了原管、半菱形管和全菱形管在不同厚度下壓潰力和位移的曲線，從圖中可以看出，當(dāng)厚度較低時(shí)，全菱形預(yù)折管的初始?jí)簼⒘Ψ逯底钚。鴪A形管最大。隨著厚度的增加，三種管子的壓潰力-位移曲線基本一致，此時(shí)全菱形管的吸能優(yōu)越性也基本沒(méi)有了。通過(guò)對(duì)比三種管子的吸能特性，全菱形預(yù)折管具有最優(yōu)的吸能特性。

的壓潰力位移曲線

3.2 半菱形預(yù)折管和全菱形預(yù)折管在不同b下吸能特性對(duì)比

為了比較不同b對(duì)其吸能特性的影響，θ應(yīng)該保持不變，對(duì)于全菱形預(yù)折管，由10可以看出，此時(shí)l應(yīng)該保持不變。在這一部分中，b分別設(shè)置成15，20，25，30，35mm，而相應(yīng)的l也設(shè)置為15，20，25，30，35mm。而對(duì)于半菱形預(yù)折管，其直徑也由（9）式計(jì)算得出。根據(jù)公式（4），為了保持θ不變，c和l的比值應(yīng)不變。因此在半菱形預(yù)折管中，c和l分別設(shè)置為12.5mm和25mm，而b也設(shè)置成15，20，25，30，35mm。如圖9所示，兩者預(yù)折管的初始峰值應(yīng)力（IPF）隨著b的增加而增大，并且全菱形預(yù)折管的曲線要低于半菱形預(yù)折管。對(duì)于比吸能（SEA），全菱形預(yù)折管隨著b的增加而減小，而半菱形預(yù)折管則隨著b的增加產(chǎn)生微弱的波動(dòng)。通過(guò)圖9可以明顯的看出全菱形預(yù)折管具有更好的吸能特性。

3.3 半菱形預(yù)折管和全菱形預(yù)折管在不同l下吸能特性對(duì)比

對(duì)于兩種預(yù)折管，b設(shè)置成25mm，l分別設(shè)置成20，25，30，35和40mm。如圖10所示，兩個(gè)預(yù)折管的IPF隨著l的增加而增加，并且全菱形預(yù)折管的IPF曲線要低于半菱形管，這就表明全菱形預(yù)折管具有更高的安全性。在SEA方面，全菱形預(yù)折管在20 < l <25區(qū)域明顯上升，隨著l的持續(xù)增加，SEA在慢慢的下降。對(duì)于半菱形預(yù)折管，其SEA隨著l的增加而產(chǎn)生微小的波動(dòng)。此外從圖10中可以看出，全菱形預(yù)折管的SEA曲面的絕大部分是高于半菱形預(yù)折管，因此說(shuō)全菱形預(yù)折管具有更高的吸能效率。

通過(guò)以上分析可以得到，全菱形預(yù)折管再不同的厚度，不同的b和不同的l時(shí)都具有更高的安全性和吸能效率，因此下一節(jié)的優(yōu)化主要是對(duì)全菱形預(yù)折管進(jìn)行優(yōu)化。

4 全菱形預(yù)折管的多目標(biāo)優(yōu)化

4.1 多目標(biāo)優(yōu)化的描述

其中D為圓管半徑，t為圓管厚度。因?yàn)轭A(yù)折管的長(zhǎng)度都在98-102mm之間，所以圓管的長(zhǎng)度被設(shè)為100mm。

4.2 代理模型

對(duì)于非線性的碰撞接觸、大變形的問(wèn)題很用數(shù)學(xué)公式的方法來(lái)得到多目標(biāo)優(yōu)化函數(shù)的表達(dá)式，而使用代理模型是解決這類(lèi)問(wèn)題的一個(gè)十分有效的方法。本文采用了RBF（radial basis function）模型來(lái)作為代理模型，因?yàn)镽BF模型具有高的效率和計(jì)算速度。為了建立精確的RBF模型，通過(guò)優(yōu)化的超拉丁立方（OLHS）抽樣方法得到了40個(gè)樣本點(diǎn)。通過(guò)計(jì)算得到樣本點(diǎn)的仿真結(jié)果，這樣就可以用RBF模型來(lái)構(gòu)造目標(biāo)函數(shù)SEA和IPF了。表4和表5分別列出了全菱形預(yù)折管和圓管的樣本點(diǎn)以及其仿真結(jié)果。

4.3 優(yōu)化結(jié)果

本來(lái)主要采用了遺傳算法2代（NSGA-II）來(lái)獲得全菱形預(yù)折管的最優(yōu)幾何參數(shù)。由于本文的優(yōu)化問(wèn)題為多目標(biāo)優(yōu)化，因此很難獲得一組最優(yōu)解，但是可以獲得一組Pareto解集，如圖13所示。研究人員可以從Pareto解集中任選一點(diǎn)作為設(shè)計(jì)點(diǎn)。盡管Pareto解集能夠給設(shè)計(jì)人員提供很多種設(shè)計(jì)點(diǎn)，但是最后還是要選擇一點(diǎn)作為最優(yōu)的解（如圖14中的拐點(diǎn)）。本文主要采用了一種最短路徑法來(lái)獲得這個(gè)拐點(diǎn)[14]，其原理為：先將Pareto圖中兩個(gè)目標(biāo)函數(shù)的最優(yōu)值的點(diǎn)作為一個(gè)理想點(diǎn)，然后Pareto曲線中距離理想點(diǎn)最近的點(diǎn)為拐點(diǎn)，也即最終選擇的優(yōu)化點(diǎn)。通過(guò)這種方法我們得到了一個(gè)最優(yōu)解，如表6所示，最優(yōu)的全菱形預(yù)折管的幾何參數(shù)為：b=10.164mm，l=27.152mm and t=1.054mm；相應(yīng)的IPF和SEA分別為14.874kN 和 9.015kJ/kg。

為了驗(yàn)證全菱形預(yù)折管吸能的優(yōu)越性，圓形管的Pareto解集也在圖13中，從圖13中可以看出，圓管的Pareto曲線的絕大部分都在全菱形預(yù)折管的上方，這就意味著菱形管的吸能特性更加優(yōu)越。

此外，本文對(duì)優(yōu)化后的結(jié)果與初始設(shè)計(jì)的結(jié)果進(jìn)行了對(duì)比，如圖15所示。在壓潰力-位移曲線中，優(yōu)化后的IPF值要明顯的比初始值要小。并且優(yōu)化后的壓潰力-位移曲線要比原始曲線要光滑，這就意味著優(yōu)化后的結(jié)構(gòu)的吸能效率更高。表7中對(duì)比了優(yōu)化前后全菱形預(yù)折管的幾何參數(shù)和仿真值，不難發(fā)現(xiàn)b和初始值有了一個(gè)很大的變化。如表6所示，優(yōu)化后的IPF和SEA要比初始設(shè)計(jì)值分別低7%和高65.5%。此外優(yōu)化前的全菱形預(yù)折管質(zhì)量為0.135kg，而優(yōu)化后的結(jié)構(gòu)只有0.079kg。因此說(shuō)優(yōu)化后的結(jié)構(gòu)不僅僅有著更高的耐撞性，而且還有著更低的重量。

4 結(jié) 論

本文主要介紹了兩種預(yù)折管，因?yàn)槠湓谳S向壓潰中具有很低IPF。文中首先介紹了兩種預(yù)折管的幾何模型，材料模型。然后建立預(yù)折管在壓潰過(guò)程中的有限元模型，根據(jù)文獻(xiàn)（6）的試驗(yàn)，驗(yàn)證有限元模型的精確性。之后對(duì)兩種預(yù)折管和普通圓管進(jìn)行吸能特性的對(duì)比，發(fā)現(xiàn)預(yù)折管比普通圓管具有更低的IPF和更高的SEA。隨后對(duì)兩種預(yù)折管進(jìn)行幾何參數(shù)的分析，發(fā)現(xiàn)預(yù)折管的b，l和t對(duì)結(jié)構(gòu)的吸能特性有著很大的影響，并且全菱形預(yù)折管要比半菱形預(yù)折管的吸能特性更加優(yōu)越。所以隨后對(duì)全菱形預(yù)折管進(jìn)行多目標(biāo)參數(shù)優(yōu)化，目標(biāo)為最大化增大SEA和降低IPF。通過(guò)OLHS抽樣方法抽取40個(gè)樣本點(diǎn)，利用樣本點(diǎn)的仿真值和RBF模型，分別建立了IPF和SEA的代理模型，最后使用NSGA-II在代理模型中求出一Pareto解集。隨后對(duì)Pareto解集采用最短路徑方法選取了一組最優(yōu)解。通過(guò)對(duì)比優(yōu)化前后全菱形預(yù)折管的吸能特性，得出優(yōu)化管具有更高的耐撞性和更低的質(zhì)量。因此，全菱形預(yù)折管是一個(gè)非常高效的吸能結(jié)構(gòu)，可以作為汽車(chē)前縱梁的結(jié)構(gòu)。

參考文獻(xiàn)：

[1] Mirzaei M， Shakeri M， Sadighi M， et al. Multi-objective optimization of crashworthiness of cylindrical tubes as energy absorbers[J]. 2011， 12（116）：5-18.

[2] Li G， Zhang Z， Sun G， et al. Crushing analysis and multiobjective optimization for functionally graded foam-filled tubes under multiple load cases[J]. International Journal of Mechanical Sciences， 2014， 89（89）：439-452.

[3] Wierzbicki T， Abramowicz W. On the Crushing Mechanics of Thin-Walled Structures[J]. Journal of Applied Mechanics， 1983， 50（4）：727-734.

[4] 蘭鳳崇，李佳光， 馬芳武，等.連續(xù)變截面板（TRB板）在汽車(chē)前縱梁中的應(yīng)用及優(yōu)化分析[J].機(jī)械設(shè)計(jì)與制造，2014（1）：25-28.

[5] Nia A A， Hamedani J H. Comparative analysis of energy absorption and deformations of thin walled tubes with various section geometries[J]. Thin-Walled Structures， 2010， 48（12）：946-954.

[6] 鐘陽(yáng). SUV側(cè)面碰撞仿真分析及B柱優(yōu)化設(shè)計(jì)研究[D].華南理工大學(xué)，2010.

[7] Sun G， Xu F， Li G， et al. Crashing analysis and multiobjective optimization for thin-walled structures with functionally graded thickness[J].International Journal of Impact Engineering， 2014， 64（64）：62-74.

[8] Yang K， Xu S， Shen J， et al. Energy absorption of thin-walled tubes with pre-folded origami patterns： Numerical simulation and experimental verification[J]. Thin-Walled Structures，2016，103：33-44.

[9] Song J， Chen Y， Lu G. Axial crushing of thin-walled structures with origami patterns[J]. Thin-Walled Structures， 2012，54（2）：65-71.

[10] Ma J.Energy Absorption of Thin-Walled Square Tubes With a Prefolded Origami Pattern—Part I： Geometry and Numerical Simulation[J]. Journal of Applied Mechanics，2014， 81（1）：1003.

[11] Ren X， Shen J， Ghaedizadeh A， et al. Experiments and parametric studies on 3D metallic auxetic metamaterials with tuneable mechanical properties[J]. Smart Material Structures， 2015， 24（95016）：（15pp）.

[12] Hanssen A G， Hopperstad O S， Langseth M， et al. Validation of constitutive models applicable to aluminium foams[J]. International Journal of Mechanical Sciences， 2002，44（2）：359-406.

[13] Guillow S R， Lu G， Grzebieta R H. Quasi-static axial compression of thin-walled circular aluminium tubes[J].International Journal of Mechanical Sciences， 2001， 43（9）：2103-2123.

[14] Sun G， Li G， Gong Z， et al. Multiobjective robust optimization method for drawbead design in sheet metal forming[J].Materials & Design， 2010， 31（4）：1917-1929.