水利水電工程施工多元協同優化模型研究
趙尹利,李艷玲,張 瀚,安慧琳
(1.四川大學水利水電學院,成都 610065; 2.四川大學水力學與山區河流開發保護國家重點實驗室,成都 610065)
0 引 言
水利水電工程地形地質條件復雜、建設周期長、涉及因素廣泛,其施工方案優化必須綜合考慮施工安全、質量、進度、投資、環境之間復雜的制約關系,并對其科學合理的管控,方能保證工程項目建設的科學性和高效性[1]。目前,國內外對五大目標的單項管控理論研究已較成熟,針對每個目標,均提出了許多科學的管理和評價方法[2,3]。近年來,眾多研究者開始針對工程施工進度、質量、成本三大目標,建立起均衡優化模型,并使用遺傳算法[4]、螞蟻算法[5]和微粒群算法[6]等多種算法進行優化求解,但是,此類模型很少定量考慮到施工安全和環境的影響。隨著社會對工程安全和環境保護意識的不斷深化,基于進度、質量和成本的傳統綜合均衡優化模型已不能滿足現代施工管理的要求。因此,本文針對施工安全、質量、進度、投資和環境五大目標,考慮其對立統一關系,選定主控因子,構建主控因子與多目標因子的多元關系函數以定量分析主控因子變化對其他目標因子的影響程度,再利用方案優選步驟實現施工方案的多因子協同優化。此模型能夠針對各個工程的不同特點定制出一套科學的優化方案,也能為其他工程領域的施工方案優化提供一定的參考價值。
1 模型構建
基于主控因子的施工多元協同優化模型的核心是建立施工安全、質量、進度、投資、環境等目標因子間的多元關系函數,實現施工方案的多因子協同優化。
1.1 多元關系函數構建
多元關系函數的構建應首先結合工程實際情況,選擇一個目標作為主控因子p,再分別構建該主控因子和其他協調因子的“目標因子-主控因子”關系函數,從而定量獲取主控因子變化對其他因子的影響程度。本文以施工進度為主控因子,構建“其他因子-進度”關系模型。
(1)質量-進度關系模型。在允許工期范圍內,適當壓縮工期對工程質量影響較小,但一旦超過極限工期,其質量水平則會迅速下降,因此可采用自然對數函數表達質量-工期關系[7],如圖1,從而構建質量-進度關系模型如式(1)。
(1)
式中:ai=(e-eQi)/(tni-tsi);bi=(eQi·tni-e·tsi)/(tni-tsi);r為項目包含的工作數;tni為工作i的正常工作時間;ti為工作i的實際工作時間;tsi為工作i的極限工作時間;φi為工作i質量權重系數;Qi為工作i實際狀態下的質量水平。
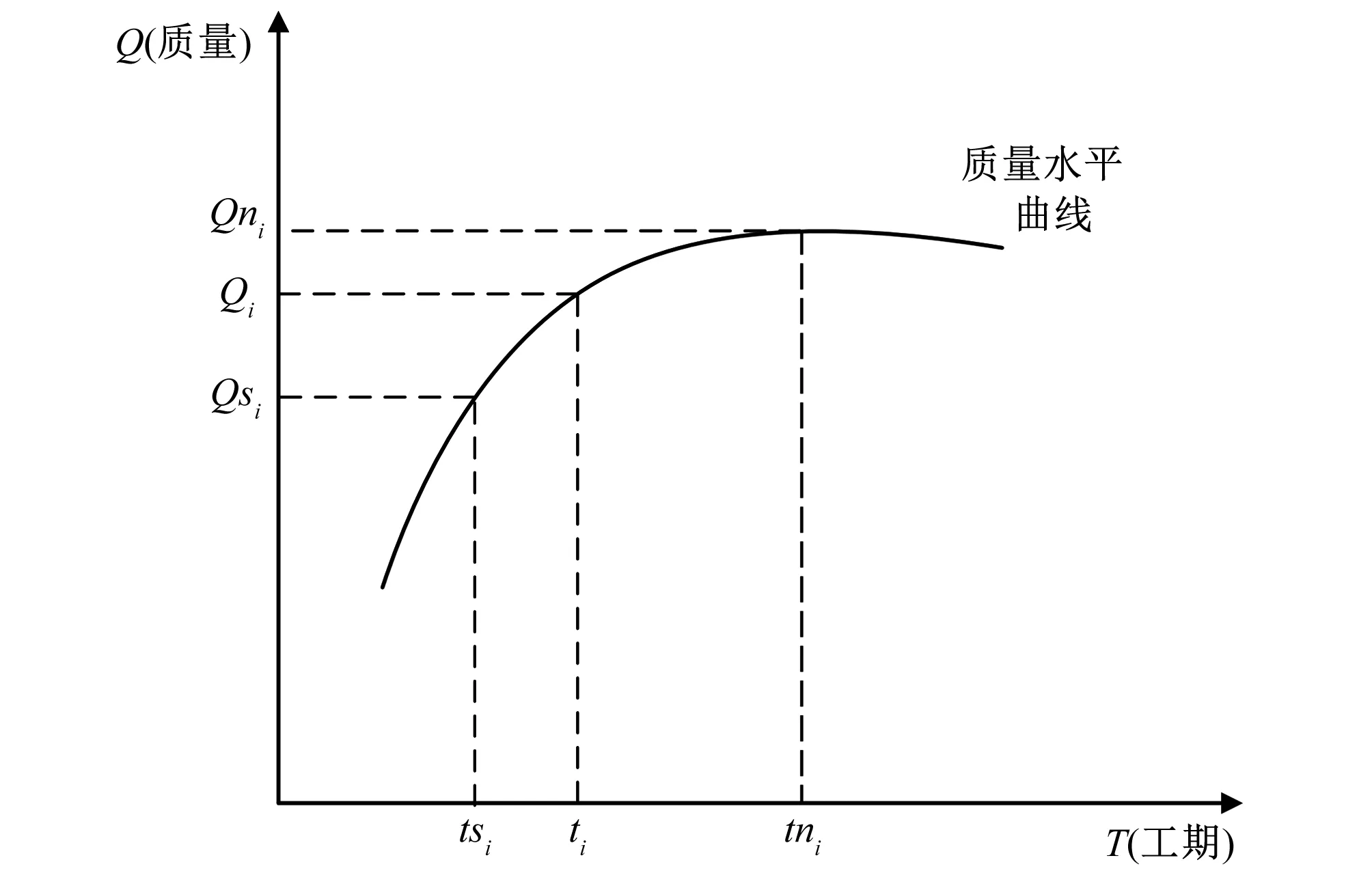
圖1 質量水平與工期關系曲線Fig.1 Relationship diagram of quality level and progress
(2)投資-進度關系模型。工程項目建設的投資費用可分為直接費用、間接費用和工期獎罰費用[8]。直接費用包括直接工程費和措施費,與工期呈二次曲線特性;間接費用包含企業管理費和規費,和工期獎懲費用會隨著工期的縮短成比例的下降,因此,直接和間接費用之和與時間呈開口向上的拋物線關系,拋物線頂點所對應的時間,即工作i的實際工作時間,產生的總投資最優。投資-進度關系曲線如圖2,關系模型如下:
(2)
式中:r為項目包含的工作數;αi為工作i的工作時間壓縮時的費用增加變化率,αi≌(Csi-Cni)/(tni-tsi);tni為工作i的正常工作時間;ti為工作i的實際工作時間;tsi為工作i的極限工作時間;Cni為工作i在正常工作時間下的直接費用;Csi為工作i在極限工作時間下的直接費用;βi為與工期有關的間接費系數(每單位時間的間接費用);β2為計算工期超過或小于合同工期的獎罰系數;T為實際工期;Th為合同工期。

圖2 投資費用與工期關系示意圖Fig.2 Relationship diagram of cost and progress
(3)安全-進度和環境-進度關系模型。安全和環境的量化指標可采用安全可靠度和環境保持度。環境-進度和安全-進度具有相同的變化關系,即工期正常情況下,適當縮短工期,工程的安全可靠度和環境保持度均下降較緩,若繼續壓縮工期超過了極限工作時間,安全可靠度和環境保持度均會直線下降。因此,本文利用線性和二次函數分段模擬其相關關系,得到安全-進度和環境-安全曲線如圖3,關系模式如式(3)。
(3)
式中:r為項目包含的工作數;tni為工作i的正常工作時間;ti為工作i的實際工作時間;tsi為工作i的極限工作時間;wi為工作i安全(環境)的重要程度;Sni為工作i在正常工作時間下的安全可靠度(環境保持度);Si為工作i實際狀態下的安全可靠度(環境保持度);Ssi為工作i極限狀態下的安全可靠度(環境保持度)。

圖3 安全可靠度(環境保持度)與工期關系示意圖Fig.3 Relationship diagram of safety reliability (Environmental retention) and progress
1.2 多因子協同優化方法和步驟
(1)建立多目標方案集。在滿足相關規定、資源可供以及不改變工程特性情況下,改變主控因子量值,得到一系列的計劃方案,再由上述關系模型,得到每個計劃方案所對應的目標因子的量值,構建出多目標方案集。例如,當以進度主控時,首先,將工期由正常工期壓縮至極限工期,得到一系列施工工期;再根據施工網絡計劃圖,利用“進度-目標因子”4個關系模型[如式(1)~式(3)],計算出各個方案施工投資費用、質量水平、安全可靠度和環境保持度,構建多目標方案集為:
(4)
(2)建立規范化賦權矩陣。首先用梯形隸屬度函數[9]將式(4)轉化為規范化矩陣,對越大越優的目標,利用升半梯形;越小越優的目標,利用降半梯形;中性目標P0,利用中間型梯形。再對矩陣進行賦權,可采用主觀賦權和客觀賦權法,其中,客觀賦權主要包括熵權法、標準離差法和CRITIC[10]等,得到加權的標準化矩陣X,xij計算如下式:
xij=wizij,i=1,2,3,…,m;j=1,2,3,…,n
(5)
(3)計算各方案灰色關聯系數。首先確定各個目標所對應的最優解X+=[x+1,x+2,…,x+m]T和最劣解X-=[x-1,x-2,…,x-m]T,其中x+i和x-i元素分別為:
x+i=max{xi1,xi2,…,xin},x-i=min{xi1,xi2,…,xin}
(6)
再計算各方案i分別與最優解和最劣解關于指標i的灰色關聯系數:
(8)
式中:ε為分辨率,0<ε<1,一般取ε=0.5。
(5)得出優化方案,即依據灰色相對貼近度對方案進行優劣排序。計算各方案與最優、最劣解的灰色關聯相對貼近度μj,再從大到小對相對貼近度進行排序,相對貼近度最大的方案即為最優方案,方案j的相對貼近度μj由下式得到:
(9)
2 工程實例
某大壩工程施工進度網絡計劃見圖4,2016年9月至2018年1月之間是該工程施工高峰期。考慮工程特點和施工要求,選擇以進度為主控目標,根據上文所構建的進度主控關系模型,進行參數的設定與生成,得到各項目相關參數如表1。

圖4 某大壩工程施工進度網絡計劃圖Fig.4 network plan of a dam project

表1 建設項目網絡計劃相關參數Tab.1 Related parameters of construction project network plan
綜合考慮施工度汛、資源配置等因素,對正常工期進行壓縮,確定出7種工期可行方案。采用式(1)~式(3)的關系函數,分別計算七種可行方案的工期、質量水平、投資、安全可靠度和環境保持度見表2。

表2 各方案工期、質量水平、投資、安全可靠度和環境保持度量值Tab.2 Project duration, quality level, investment, safety and reliability and environmental maintenance
依據上文構建的進度主控的多元管控模型,多目標矩陣P為:
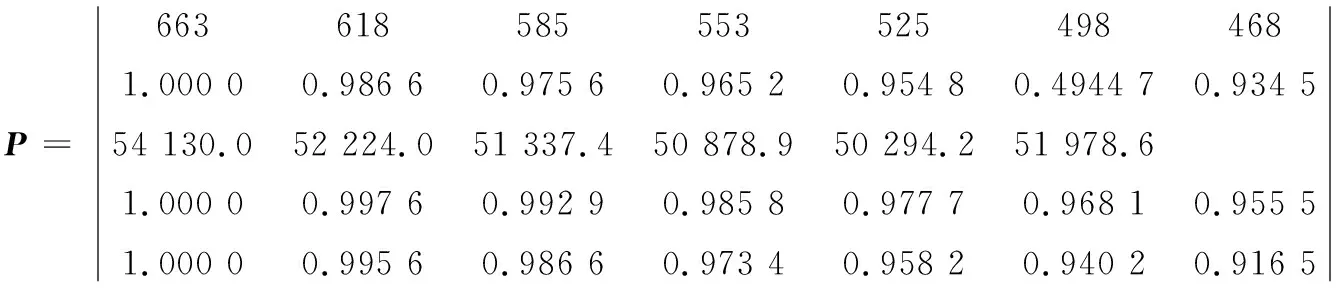
把目標特征值矩陣轉換為規范化矩陣R:
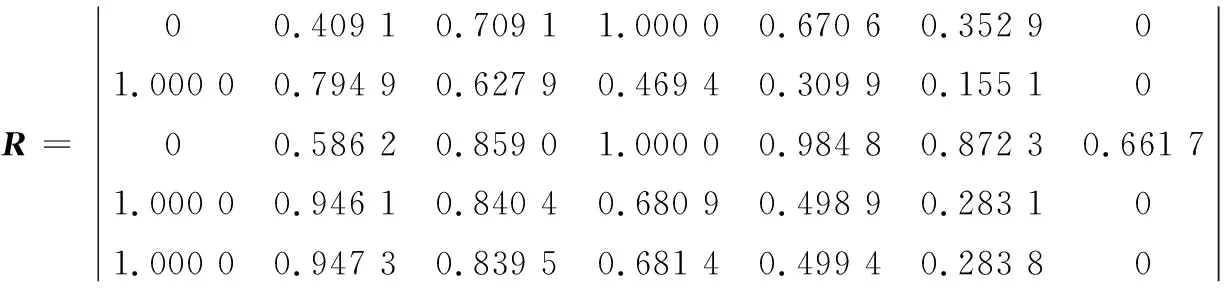
采用標準離差法對工期、質量、投資、安全和環境五個目標進行賦權,再參照本建設項目對五大控制目標的偏好權重,對此權重向量進行修正,其修正后向量為:
C=(0.25,0.25,0.25,0.15,0.10)
根據式(6)可以確定各個目標所對應的最優解X+=(0.25,0.25,0.25,0.15,0.10)T,X-=(0,0,0,0,0)T。
計算各方案與最優解X+的灰色關聯度r+為:r+=(2.676 8,2.625 7,2.829 5,3.276 9,2.738 1,2.908 3,1.929 7),各方案與最劣解X-的灰色關聯度r-為:r-=(3.343 4,2.520 0,2.462 8,2.547 9,2.907 7,3.441 7,4.430 4)。
計算各方案與最優、最劣解的灰色關聯相對貼近度μj:
μj=(0.444 6,0.510 3,0.534 6,0.562 6,
0.485 0,0.401 4,0.303 4)
最后根據其相對貼進度的大小對本建設項目的7個可行的方案進行排序,其排序的結果為:
方案4>方案3>方案2>方案5>方案1>方案6>方案7
相對貼近度最大的方案即為最優方案,因此本建設工程此時間段內進行目標控制的最優方案為方案4,其工期即為553 d,費用為50 878.9 萬元,質量水平為0.965 2,安全可靠度為0.985 8,環境保持程度為0.973 4。
3 結 論
本文提出的基于主控因子的施工多元協同優化模型能定量考慮該五大施工目標的綜合影響,實現施工方案的多因子協同優化,可大幅提升決策結論的合理性和客觀性。該模型運用于實際工程時,可根據每個工程不同的特點和需求選取合適的主控因子,并建立不同主控因子與其他協控因子的關系函數,為施工智能管控系統的研發奠定一定的理論基礎。
□

