平、逆坡渠道中污染物輸移擴散研究

朱 杰，權 錦，龍 巖，雷曉輝，孔令仲

(1.北京工業大學，北京 100022；2.中國水利水電科學研究院，北京 100038)

0 前 言

突發水污染事件一般發生突然，污染危害較大，難以控制[1]。研究突發水污染事件的關鍵，在于研究事故發生后，水流的特性以及污染物在水體中的輸移擴散過程[2, 3]。現階段研究水流特性以及污染物輸移擴散規律的主要方法有：理論分析、模型試驗和數值模擬等[4]。理論分析方法主要是建立水流運動方程和污染物輸移擴散方程，從而得到方程解析解[5, 6]；模型試驗是一種重要研究手段[7, 8]，但是模型比尺效應[9]問題至今未能得到很好解決；數值模擬是一種較高效的研究方法，比物理模型、試驗建模速度快、周期短，計算效率通常取決于計算機的CPU效率，數值模擬便于修改模擬工況，能展現多種工況下的情景，因此，用數值模擬來研究污染物在水體中的輸移擴散過程越來越被廣泛應用[10, 11]。

高學平、張晨[11]等運用數值模型對引黃濟津調水工程河道水質進行了預測，并根據污染物峰值濃度的變化情況，分析了污染物輸移擴散及降解轉化規律。房彥梅等[12]利用一維水力學和水質數值模型方法對南水北調中線工程典型渠段突發性水污染事故應急控制策略進行了數值模擬，分析不同控制策略下渠道退水量、穩定時間、水位變幅、水質等參數的變化情況，制定保證明渠安全運行的水污染事故應急閘控方案，為中線工程應急預案的建立提供參考。宋國棟[13]以南水北調中線污染物運移特性研究為背景，在現場調查及模型試驗模擬的基礎上，研究了突發性水污染事件發生后污染物的輸移規律，并給出了突發性水污染事件發生后的處置措施。王興偉等[14]應用Mike水質模型軟件對污染物在干渠內的污染擴散情況進行模擬，對突發事故的影響范圍、程度、時間做出定量預報，揭示突發事故發生后，節制閘未參與調控情況下的污染物輸移擴散規律。張秋燕[15]研究了河流中污染物隨時間和空間輸移擴散的規律及其影響因素，并建立了一維恒定流水質模型，通過隱式有限差分法求解該模型。此外，張秋燕以BOD5為預測因子，將數值模擬結果與QUAL2K綜合水質模型軟件的模擬結果進行比較，數值模擬與軟件模擬結果基本吻合，表明所建立的水質模型能夠較準確的模擬河流中污染物輸移擴散規律。

突發水污染事件[16]具有突發性、多樣性及不確定性，突發水污染事件發生后，需要快速采取有效的響應措施[17-19]，因而快速預測[20]出污染團的輸移擴散特征指標，對科學、高效的制定出響應策略非常重要。然而目前污染物輸移擴散研究多數集中在天然河流或者人工調水渠道的順坡段，對平坡和逆坡的渠道中污染物輸移擴散研究相對較少。

本文運用HECRAS軟件進行數值模擬，分析平坡和逆坡輸水渠道的污染物輸移擴散規律；并依據現有的長距離輸水渠道污染物輸移擴散快速計算公式(龍巖[21, 22]，主要面向順坡渠道突發水污染計算)，分析該快速計算公式在平坡和逆坡輸水渠道中的適用性，研究結果為長距離輸水工程突發水污染事件應急調控提供快速決策支持。

1 情景設置

1.1 渠段方案設置

南水北調中線全長1 432 km，總干渠渠道主要為全斷面混凝土襯砌的梯形斷面，渠道底寬由28.5 m遞減為7 m，渠道的邊坡系數也是在不斷變化的，渠道的邊坡系數變化范圍是0～3.5，其中邊坡系數為2占44%；中線全線采用順坡渠道，底坡變化范圍大概是1/30 000～1/10 000，渠道底坡有80%以上的位于區間1/30 000～1/2 000。南水北調東線輸水干線總長1 156 km，建設13個梯級泵站，全線最高處東平湖水位與長江水位差約40 m，渠道底坡為逆坡和平坡。本文以南水北調中線干線渠道斷面特征為基礎，分別采用底坡為平坡和逆坡的渠道作為研究對象，渠道的基本要素和初始條件如表1所示。

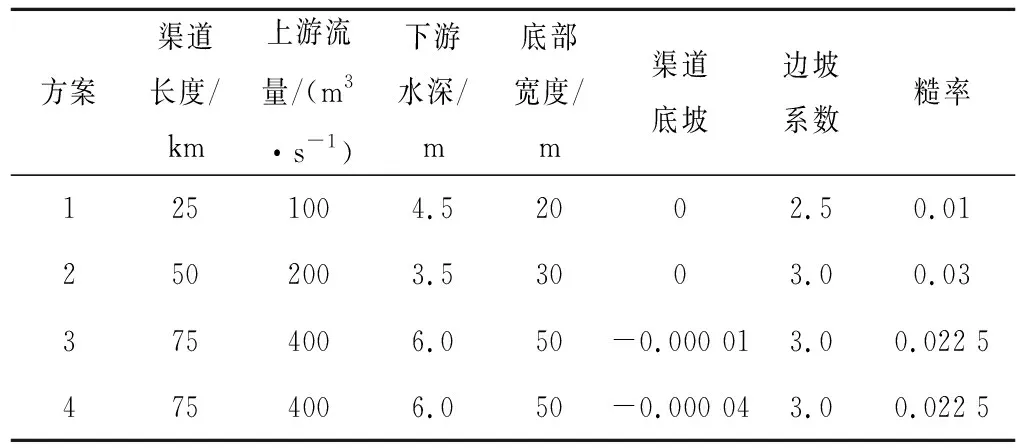
表1 渠道的基本要素表Tab.1 Basic elements of the channel

1.2 污染情景設置

艾恒雨[23]對2001-2011年國內發生的1 176起重大突發性水污染事件進行統計分析，得出突發性水污染事件的主要污染物是工業廢水、綜合廢水和油類，分別占比31%、14%和13%；并且污染水團的排放量一般能達到數百公斤到數十噸之間。

基于此研究，本文假定污染情景為可溶性污染物、量級為10 t。在數值模擬中，渠道的離散系數取值根據經驗公式[21, 24, 25]計算所得。

渠道內突發可溶性水污染事件的污染水團模擬特征如表2所示。

表2 渠道內突發可溶性水污染事件的污染水團模擬特征Tab.2 Simulation characteristics of polluted water masses in sudden water pollution incidents in channel

2 污染物水動力水質擴散模擬模型

2.1 傳統計算：一維水動力水質模型

采用美國陸軍工程兵團開發的河道水力分析軟件HEC-RAS，構建一維水動力水質模型。在軟件中，水動力運動方程和污染物輸移擴散方程為:

(3)

式中：c為污染水團濃度，mg/L；c0為側向入流濃度，mg/L；g為重力加速，m/g2；q為單位長度渠道上的側向入流流量，m2/s；t為時間，s；x為空間距離，m；z為水位，m；A為過流面積，m2；C為謝才系數，m1/2/s；DL為縱向離散系數，m2；Q為渠道流量，m3/s；R為水力半徑，m；S為源匯項。

2.2 快速計算：順坡渠道中污染物輸移擴散快速計算公式

基于正常輸水情況下的污染物輸移擴散規律，通常用污染物峰值輸移距離、縱向長度和峰值濃度來描述污染物的輸移擴散過程。圖1中給出了污染物峰值輸移距離、縱向長度以及峰值濃度的涵義。

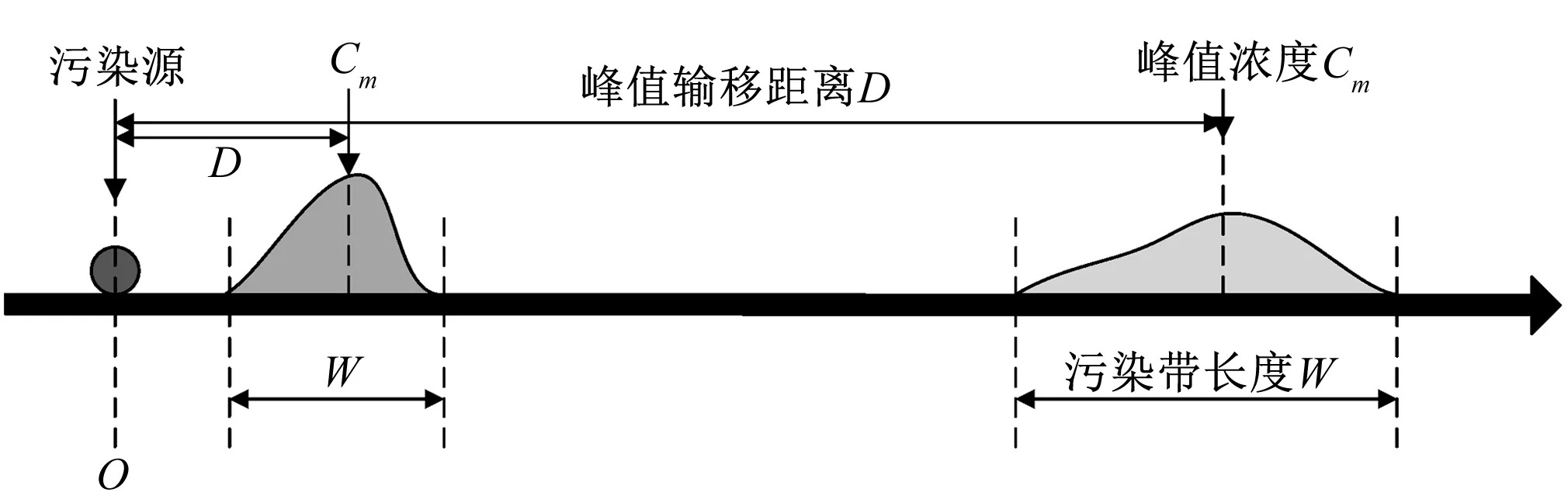
圖1 污染物輸移擴散特征Fig.1 Pollutant transport characteristics

2.2.1 峰值輸移距離快速計算公式

研究發現[22]峰值輸移距離與渠道長度、底坡、流量以及傳播時間成正比，與渠道邊坡系數、底寬和水深成反比，但渠道的長度、底坡對峰值輸移距離影響甚微，而流量與渠道流速成正比，邊坡系數、底寬和水深與渠道流速成反比，因此認為峰值輸移距離與渠道流速、水流的傳播時間成正比，其關系式[22]為：

D=vT

(4)

式中：D為峰值輸移距離，m；v為渠道內水流速度，m/s；T為傳播時間，s。

2.2.2 污染物縱向長度快速計算公式

根據文獻[26]可知，一維瞬時污染物擴散中，污染物濃度隨流動時間呈正態分布。由正態分布曲線間的面積比例可知：在4σ(σ為正態分布的標準差)范圍內包含污染物總量的95.44%，在6σ范圍內包含污染物總量的99.74%，定義kσ為污染物離散寬度(k為離散寬度系數)。

T時間內污染水團沿渠道縱向長度W可表達[27]為：

(5)

式中：DL為縱向離散系數，m2/s；t為時間，s；a為k/2。

2.2.3 污染物峰值濃度快速計算公式

峰值濃度[27]為：

(6)

假設初始濃度為C0，某時刻峰值濃度為Cm，M為污染物投放量，則定義P為峰值濃度與初始濃度百分比，即：

(7)

經該提出者驗證，該公式對突發水污染事件下長距離順坡輸水渠道的污染物輸移擴散模擬效果良好。但并未研究逆坡、平坡渠道中的適用性。

3 平坡渠道中污染物輸移擴散研究

為研究平坡渠道中的污染物輸移擴散，本文設置了兩種平坡渠道方案(渠段長度為25 km和50 km。)和污染情景，平坡渠道參數如表1所示。

3.1 污染物峰值輸移距離研究

經模擬計算及運用快速計算公式計算，污染物峰值輸移距離D模擬值及計算值對比結果如圖2所示。可以看出，當渠道底坡為平坡時，峰值輸移距離D與污染物擴散時間成正比，與渠道長度成反比； HECRAS軟件模擬值與順坡快速計算公式計算值變化過程基本一致，計算結果較為接近，偏差值較小。

計算值與模擬值的偏差如圖3所示。可以看出，渠段長度為25 km時，偏差值小于5%；渠段長度為50 km時，模擬值與計算值的偏差小于20%。因此，在渠道底坡為平坡時，污染物峰值輸移距離可以用順坡渠道峰值輸移距離快速計算公式進行預測，當渠段長度規模為25 km以下時，預測效果較好，渠段越長，偏差值越大。

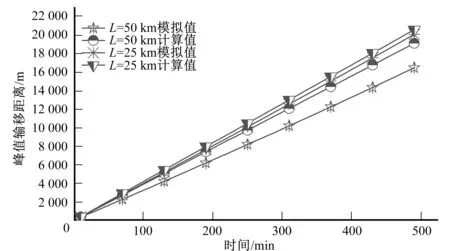
圖2 平坡渠道計算值與模擬值對比Fig.2 Comparison of calculated values of flat slope channels with simulated values

圖3 平坡渠道計算值與模擬值偏差Fig.3 Deviation between calculated value and simulated value of flat slope channel

3.2 污染物縱向長度研究

經模擬計算及運用快速計算公式計算，污染物縱向長度W隨傳播時間的變化過程的模擬結果及計算結果如圖4所示。可以看出，當渠道底坡為平坡時，污染物縱向長度隨時間成正相關變化，且隨時間的增加，渠道越長，污染物縱向長度就越大，但不同長度的渠道間差別較小。模擬值與計算值的變化規律基本相同，數值較為接近。

對模擬值與計算值的偏差進行比較分析(圖5)，可以發現，快速計算公式計算值與模擬值在渠段長度為25 km時的相對偏差在5%左右，在渠段長度為50 km時，偏差值低于10%。因此，順坡渠道污染物縱向長度快速計算公式可用于平坡渠段可溶性污染團的污染物縱向長度指標快速預測，且效果較好。

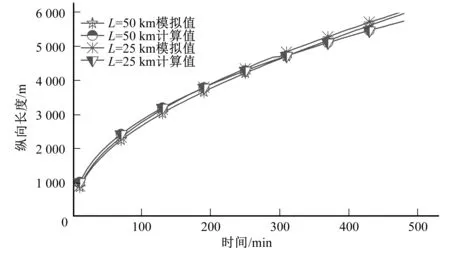
圖4 平坡渠道計算值與模擬值對比Fig.4 Comparison of calculated values of flat slope channels with simulated values

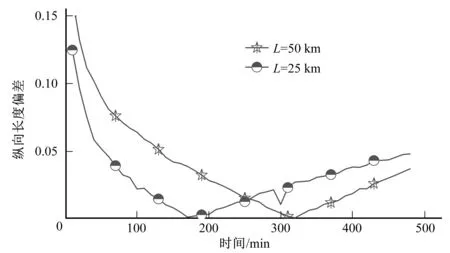
圖5 平坡渠道計算值與模擬值偏差Fig.5 Deviation between calculated value and simulated value of flat slope channel

3.3 污染物峰值濃度研究

經模擬計算及運用快速計算公式計算，污染物峰值濃度C模擬值及計算值對比結果如圖6所示。

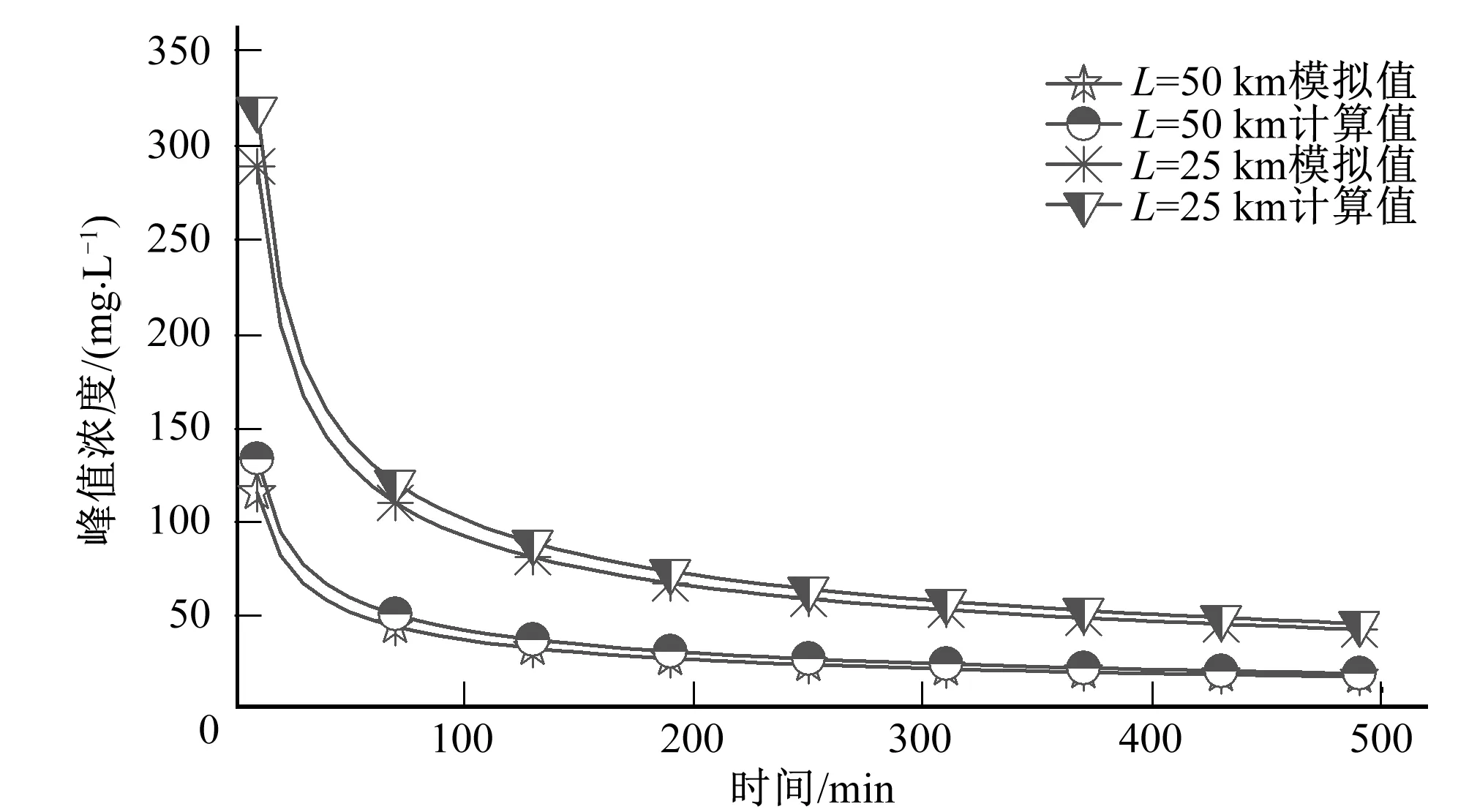
圖6 平坡渠道峰值濃度模擬值與計算值對比Fig.6 Comparison of simulated peak value and calculated value of flat slope channel

從圖中可以看出，相同離散系數下，污染團峰值濃度與時間成反比，同種底坡情況下，污染團峰值濃度與渠道長度成反比。快速公式計算值與模擬值高度吻合，基本一致。圖7反映了平坡情況下，某一時刻的濃度值與初始濃度的比值P的變化過程，可以看出，濃度比值P隨時間的增加逐漸減小，反映了污染物濃度逐漸降低，這與圖6的結果相吻合。同時圖7還可以看出，模擬值與快速公式計算得到的P值結果接近，偏差值較小。因此，在渠道底坡為平坡時，污染物峰值濃度及濃度比值P仍然可以用順坡渠道快速計算公式計算，且效果較好。

圖7 平坡渠道濃度比值P模擬值與計算值Fig.7 Flat slope channel simulation and concentration ratio of P value

對污染團峰值濃度的模擬值與計算值偏差進行比較分析(圖8)，可以發現，快速計算公式計算值與模擬值在渠段長度為25 km時的相對偏差低于10%，在渠段長度為50 km時，偏差值在12%左右，兩種方案的偏差都有逐步減小的趨勢。峰值濃度比值P模擬值與計算值的偏差對比如圖9。從圖9中可以看出，渠段長度為25 km時的偏差在10%以下，渠段長度為50 km時偏差在12%左右，且偏差逐漸減小。因此，平坡渠道污染物峰值濃度及濃度比值P的快速預測可以用順坡渠道快速計算公式，且效果較好。

圖8 平坡渠道峰值濃度模擬值與計算值偏差Fig.8 Simulation flat slope channel peak concentration and calculated deviation

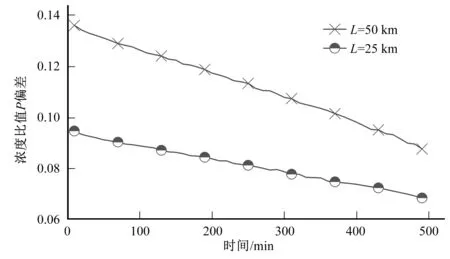
圖9 平坡渠道濃度比值P模擬值與計算值偏差Fig.9 Simulation flat slope channel concentration ratio and the calculated value of the deviation of P

4 逆坡渠道中污染物輸移擴散研究

為研究逆坡渠道中的污染物輸移擴散，本文設置了兩種逆坡渠道方案(渠段底坡為-0.000 01和-0.000 04。)和污染情景，逆坡渠道參數如表1所示。

4.1 污染物峰值輸移距離計算與分析

經模擬計算及運用快速計算公式計算，污染物峰值輸移距離D模擬值及計算值對比結果如圖10所示。從圖結果所可以看出，在逆坡渠道的不同方案下，污染團峰值輸移距離D與污染物擴散時間呈線性關系，并與渠道底坡坡度成反比。

HECRAS軟件模擬值與快速計算公式計算值變化情況一致，變化過程較接近，偏差較小。計算值與模擬值的偏差如圖11所示，渠道底坡為-0.000 04時(方案4)，偏差在20%左右，且隨時間的推移，偏差越來越小；當底坡為-0.000 01時(方案3)，偏差在12%左右，且逐漸減小。因此，順坡渠道峰值輸移距離快速計算公式可用于快速預測逆坡渠道污染物峰值輸移距離，且效果較好。

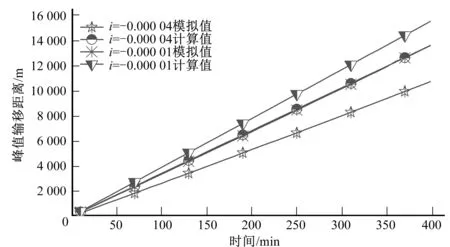
圖10 逆坡渠道計算值與模擬值對比Fig.10 Comparison of calculated value and simulated value of reverse slope channel

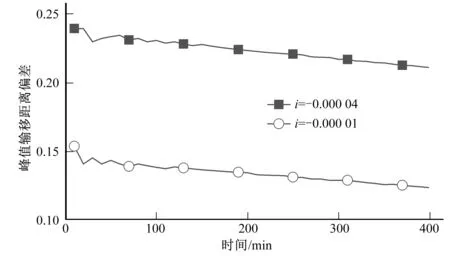
圖11 逆坡渠道計算值與模擬值偏差Fig.11 Deviation between calculated value and simulated value of reverse slope channel

4.2 污染物縱向長度研究

經模擬計算及運用快速計算公式計算，污染物縱向長度W模擬值及計算值對比結果如圖12所示。污染物縱向長度隨時間成正相關變化，不同底坡的渠道間縱向長度差別較小。模擬值與計算值的變化規律基本一致，數值較為接近。

圖13反映了運用順坡渠道污染物快速計算公式計算值與模擬值的相對偏差值，可以發現，渠段底坡為-0.000 01和-0.000 04時，運用快速計算公式得到的結果與模擬結果相對偏差均在10%左右，且隨時間增加，偏差值逐漸減小。因此，可以用順坡渠道污染物縱向長度快速計算公式快速預測逆坡渠道中污染物的縱向長度，且效果較好。

圖12 逆坡渠道計算值與模擬值對比Fig.12 Comparison of calculated value and simulated value of reverse slope channel

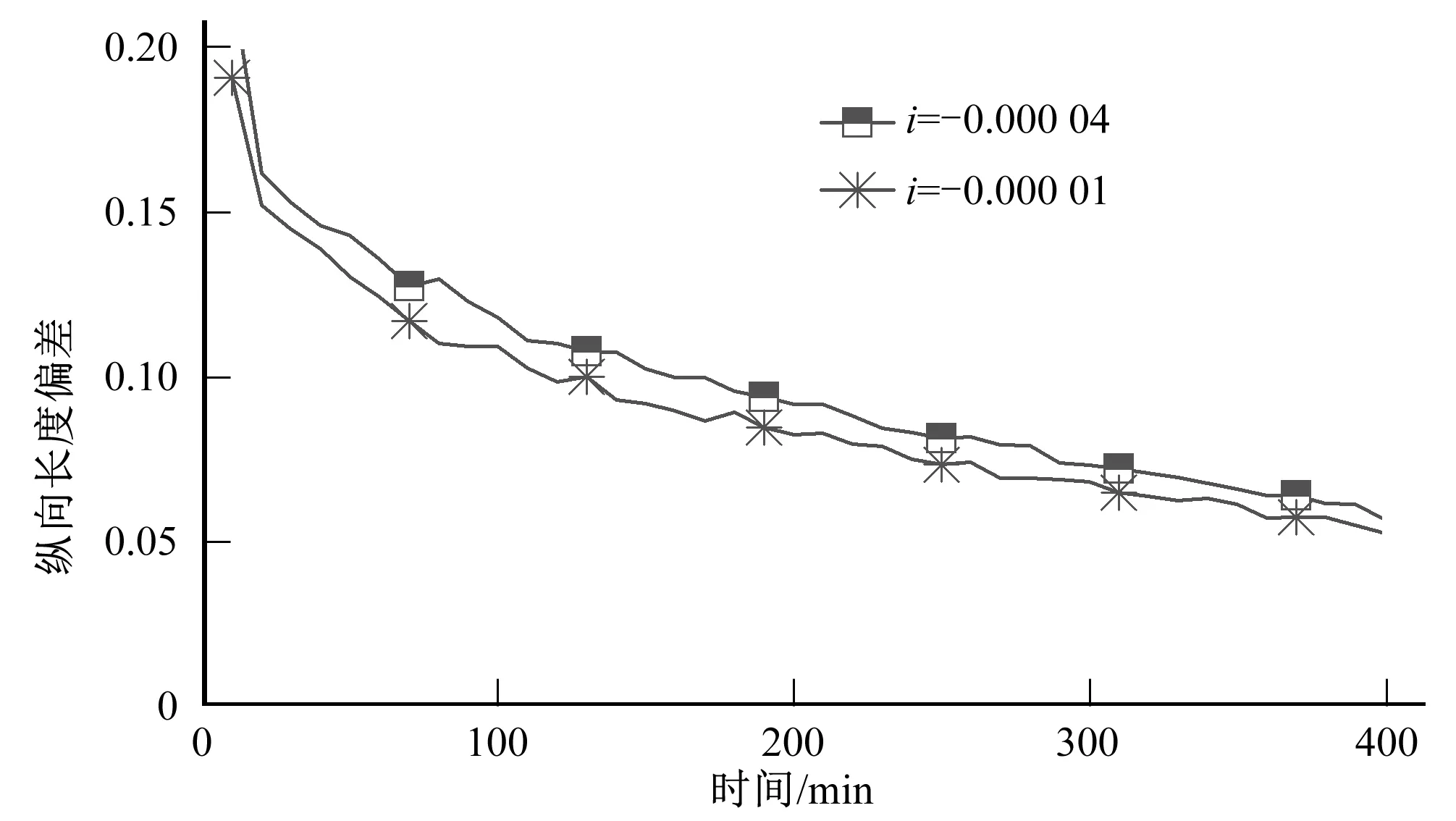
圖13 逆坡渠道計算值與模擬值偏差Fig.13 Deviation between calculated value and simulated value of reverse slope channel

4.3 污染物峰值濃度研究

經模擬計算及運用快速計算公式計算，污染物峰值濃度C模擬值及計算值對比結果如圖14所示。

從圖中可以看出，相同離散系數下，污染物峰值濃度與時間成反比。快速計算公式計算值與模擬值變化過程基本一致，峰值濃度隨時間的增加逐漸降低。圖15反映了逆坡情況下，某一時刻的濃度與初始濃度的比值P的變化過程，濃度比值P隨時間的增加逐漸減小，意味著污染物濃度逐漸降低，與圖14所反映出來的結果一致，圖15中，模擬值與快速公式計算得到的峰值濃度P值結果接近，偏差值較小。

對污染團峰值濃度的模擬值與計算值偏差進行比較分析(圖16)，可以發現，快速計算公式計算值與模擬值在渠道底坡為-0.000 04時的相對偏差低于5%，渠段底坡為-0.000 01時，偏差值在10%左右。峰值濃度比值P模擬值與計算值的偏差對比如圖17。從圖中可以看出，渠段底坡為-0.000 04時的偏差在5%以下，渠段底坡為-0.000 01時偏差在10%左右，且偏差逐漸減小。因此，逆坡渠道污染物峰值濃度及濃度比值P的快速預測可以運用順坡渠道快速計算公式，且效果較好。

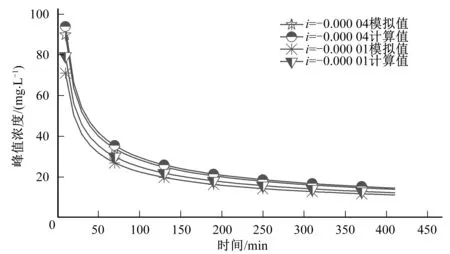
圖14 逆坡渠道峰值濃度模擬值與計算值對比Fig.14 Comparison between simulated value and calculated value of peak concentration in reverse slope channel

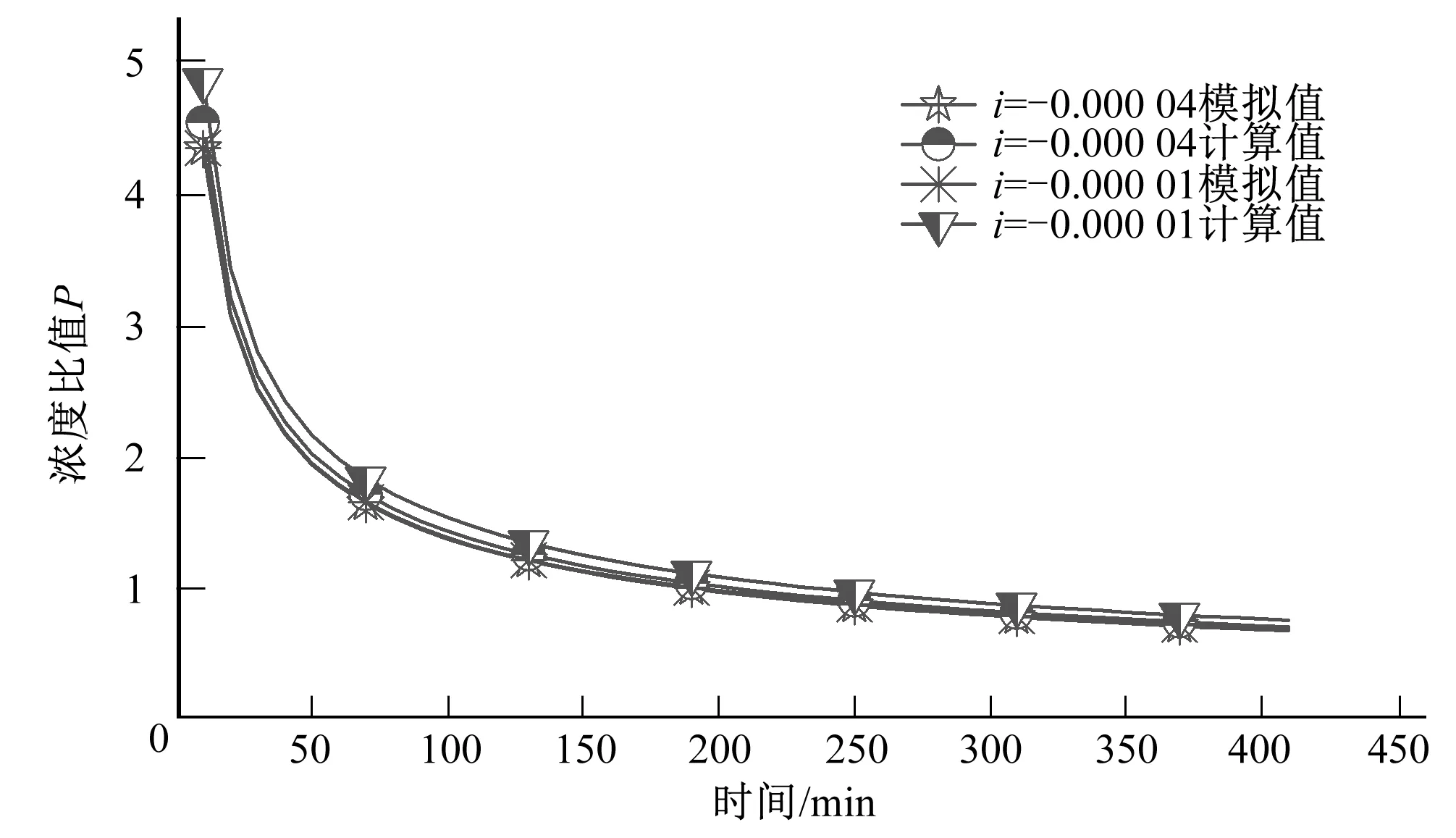
圖15 逆坡渠道濃度比值P模擬值與計算值Fig.15 P simulation value and calculation value of the concentration ratio of reverse slope channel

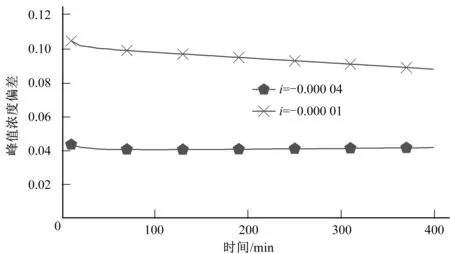
圖16 逆坡渠道峰值濃度模擬值與計算值偏差Fig.16 Deviation between simulated peak value and calculated value of reverse slope channel

圖17 逆坡渠道濃度比值P模擬值與計算值偏差Fig.17 Inverse slope channel concentration ratio P simulation value and calculation deviation

5 結 論

總結國內外對于污染團輸移擴散的研究成果，開展平、逆坡渠道中的污染物輸移擴散研究，基于已有的順坡渠道污染物輸移擴散快速計算公式，研究其在平坡、逆坡渠道情況下的適用性，并將計算結果與HECRAS軟件模擬結果進行對比，嘗試尋求平、逆坡渠道中污染物輸移擴散的快速計算方法；利用HECRAS軟件進行一維水動力水質數值模型模擬，研究了平坡和逆坡渠道中污染物峰值輸移距離、縱向長度及峰值濃度變化規律，并與順坡渠道快速計算公式計算值進行了對比，結果表明：

(1)渠道為平坡和逆坡時，峰值輸移距離的模擬值與計算值有一定差別，當渠段規模為25 km以下時，偏差值在5%以下，當渠段規模為50 km時，偏差值在20%以下，因此，順坡渠道峰值輸移距離快速計算公式適用于平坡或逆坡渠道，并在渠段規模小于25 km時計算效果較好。

(2)在計算平坡或逆坡渠道的污染物縱向長度時，模擬值與順坡渠道計算公式相吻合，偏差值在10%左右，因此，可以用順坡渠道污染物縱向長度快速計算公式快速預測平坡和逆坡渠道的污染物輸移擴散指標，且效果較好。

(3)在相同的離散系數下，平坡或逆坡渠道中，污染物峰值濃度數值模擬值與運用順坡渠道快速計算公式計算值基本一致，因此，在快速預測平坡和逆坡渠道中的污染物峰值濃度及濃度比值P值時，可以用順坡渠道快速計算公式計算。

□