中國綜合運輸網絡拓撲結構及其魯棒性研究*

高 佩 姚紅光

(上海工程技術大學航空運輸學院 上海 201620)

0 引 言

綜合運輸網絡是指包含“鐵路、公路、水路、航空和管道”等多種運輸方式，由多種運輸方式的節點和線路連接而成，通過多種運輸方式相互協作實現“旅客、貨物”從始發地到目的地位移服務的空間網絡結構.

綜合運輸網拓撲結構及魯棒性研究，目前已成為研究熱點：段后利等[1]對城市公交網絡的統計特征進行了實證研究，測算出相關統計特征參數，并通過與隨機網絡對比研究了城市公交網絡的特點.程書恒等[2]對集裝箱海運航線的網絡特征進行了研究，通過數值模擬，計算了網絡的度分布、簇系數、平均路徑長度等指標.田煒等[3]對全球航運網絡特征進行了分析，通過對全球航運網絡節點度分布、度值相關性和度與介數相關性分析發現，度值大的節點優先與度值較大節點連接，度值大的節點介數也較大，因而度值較大的節點對網絡影響程度較大.鄧亞娟等[4]以中國公路網絡為研究對象，分析了公路網絡拓撲結構的統計特征.劉宏鯤[5]則對中國航空網絡的統計特征進行了研究，指出了航空網絡的度分布具有雙截尾冪律分布的特征.文獻[6]采集了中國航空網絡的節點和航線數據信息，測算出了網絡的基本統計特征參數.上述研究都從不同側面反映了開展交通運輸網絡統計特征研究的必要性，然而目前的研究僅限于某一特定運輸領域，對于由多種運輸方式構成的綜合運輸網絡，其網絡的統計特征研究成果尚比較匱乏.

1 中國綜合運輸網絡模型的構建

1.1 中國綜合運輸網絡的數據采集

1) 節點信息的采集 將地級市以上行政區作為綜合運輸網絡的節點，因部分地區與地級市存在包含關系，為統計方便，將二者合并；共采集684個節點城市.

2) 運輸線路信息的采集 以684座節點城市為基礎，采集其之間的“鐵路、公路、航空、水運”線路，供采集到鐵路線路648條，干線(國道)公路68條、高速公路79條、國內航線2 198條、內河航道25條.

1.2 中國綜合運輸網絡的鄰接矩陣的建立

鄰接矩陣是網絡分析中最常使用的數據存儲形式，其特征是正方陣.在此方陣中，行和列都代表完全相同的網絡節點，并且行和列排列的順序相同，矩陣中的要素代表節點之間的關系，以這種形式來表示網絡關系的數據集合被稱為鄰接矩陣，記作X.根據矩陣中要素的不同含義，鄰接矩陣可以分成不同的類別.

1) 結構鄰接矩陣 結構鄰接矩陣主要用來反映綜合運輸網絡中各節點的實際連接狀況，在該矩陣中“空間上有線路直接相連的兩座節點城市對應的元素為1，其余元素為0”，記為X1.

2) 服務鄰接矩陣 服務鄰接矩陣是以能否實現相關服務作為判斷兩個節點城市是否存在相互關系的標準.若兩個節點城市之間可以進行運輸服務，則其對應的元素是否為1；否則為0，記為X2.

3) 頻次鄰接矩陣 頻次鄰接矩陣用來反映綜合運輸網絡中節點間開展運輸活動的便利程度，該矩陣通過以兩點間運輸服務日班次為權重，對“服務鄰接矩陣”加權得到，記為X3.

2 中國綜合運輸網絡結構的基本統計特征分析

2.1 中國綜合運輸網絡中節點“度”值的實證研究

2.1.1復雜網絡中“度”值解析

網絡中節點i的度ki定義為：與節點i相接的邊的總數.在網絡中，一個節點的度越大就意味著與其相連的其他節點越多，其擁有的邊數也就越多，也就意味著該節點在網絡中具有更重要的作用.網絡中所有節點i的度ki的平均值成為網絡的平均度，見式(1).

(1)

式中：N為網絡的節點數

2.1.2中國綜合運輸網絡中節點“度”值測算

不同鄰接矩陣算計出的節點的度值所代表的含義也不相同.其中，根據X1計算出的節點度值表示“網絡中與該節點空間相鄰的節點城市的數量”；根據X2計算出的節點度值表示：“網絡中與該節點有運輸線路相連的節點城市數量，即通過該節點可以不經中轉而直達的城市的數量”.根據X3計算出的節點度值表示：“該節點共擁有的運輸班次總數”.

利用不同的鄰接矩陣，借助復雜網絡專業分析軟件UCINET，計算出綜合運輸網絡中各個節點在不同鄰接矩陣中的度值，度值排名前10的節點城市見表1.

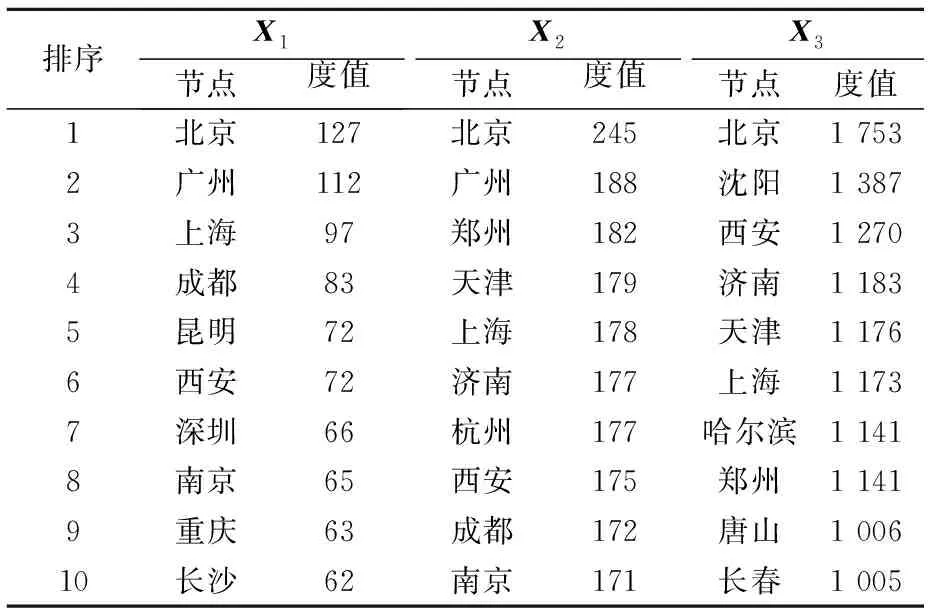
表1 各鄰接矩陣中節點城市的度值

2.2 中國綜合運輸網絡中 “度”分布情況研究

度分布函數反映的是復雜網絡系統的宏觀統計特征.綜合運輸網絡的結構特征可用分布函數P(k)來描述，P(k) 為具有相同度k的節點的出現概率，即一個任意選擇的節點度為k的概率.利用UCINET軟件，通過計算各節點度值，可以統計出網絡的度分布情況.

其中X1的度分布見圖1.該網絡中節點度值服從冪律分布.即

P(K)～ak-r

通過數值擬合得到度分布函數為P(K)=0.404 3k-1.307，其中R2=0.901.

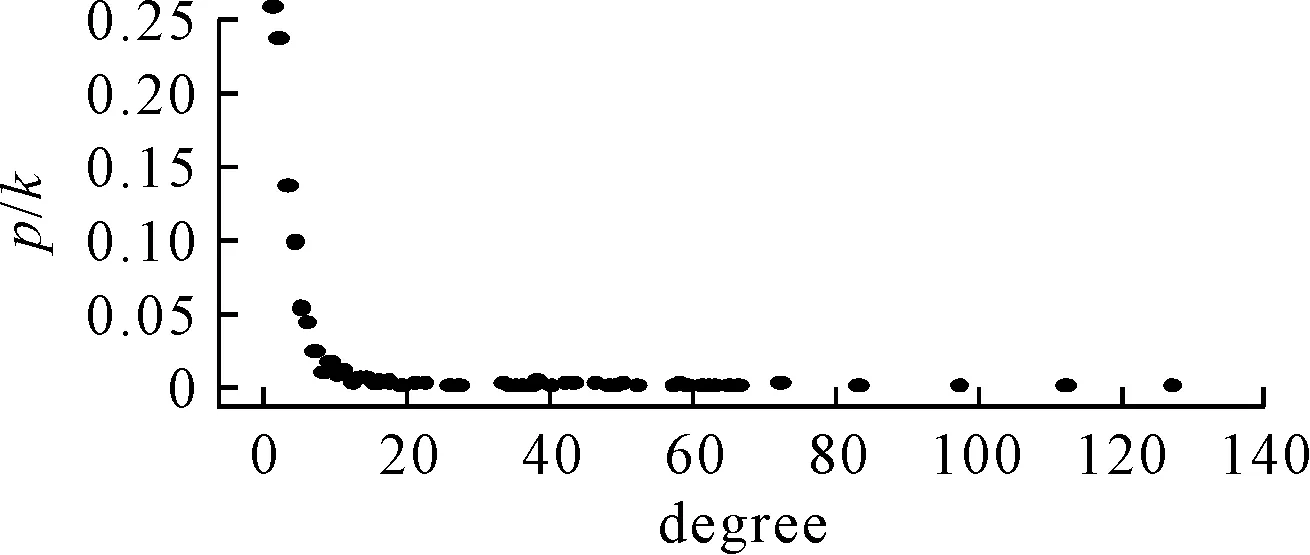
圖1 中國綜合運輸網絡的結構鄰接矩陣度分布圖

對圖1中各節點的橫、縱坐標取對數，可以得到X1對數坐標系下的節點度分布，見圖2.

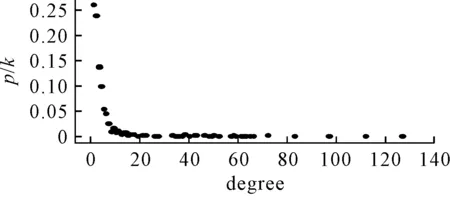
圖2 中國綜合運輸網絡的結構鄰接矩陣度分布圖(對數坐標系)

由圖2可知，中國綜合運輸網絡節點的度分布在對數坐標系下成直線遞減形似，反應了網絡具有顯著的無標度網絡特征.

按照同樣的方法，可以得到X2,X3普通坐標系和對數坐標系下的度分布情況見圖3～4.

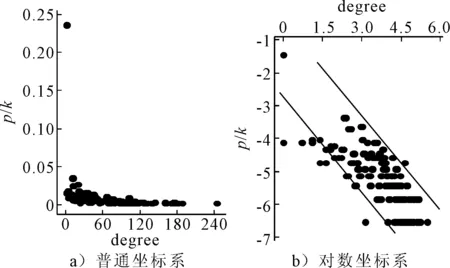
圖3 X2鄰接矩陣度分布圖

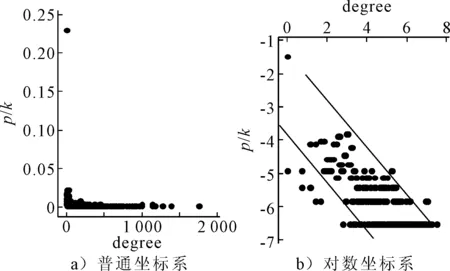
圖4 X3鄰接矩陣中度分布圖

通過數值擬合得到X2矩陣度分布函數為：P(K)=0.1 685k-0.859；X2矩陣度分布函數為：P(K)=0.1 310k-0.784.其度分布函數均隨度值呈顯著線性下降趨勢，因此可判斷上述兩種網絡亦具有顯著的無標度網絡特征.

綜上所述，實證研究結果表明：中國綜合運輸網絡三種鄰接矩陣的其網絡結構特征均表現出顯著的無標度網絡特征，其冪律系數介于[0.7，1.5]之間；上述結果表明：在中國綜合運輸網絡中，節點度值分布極不均衡，少數節點的度值很大，在網絡中發揮著關鍵作用；而大多數節點，度值較少，僅能起到某些方面的輔助作用.

2.3 中國綜合運輸網絡的平均最短路徑長度的實證研究

網絡的平均最短路徑長度L用來反映任意兩個節點之間邊的平均值.在綜合運輸網絡分析中，可以用該參數反映網絡中物資在從始發地到目的地流通過程中的中轉次數.根據鄰接矩陣的含義，應針對矩陣X2測算其平均最短路徑.

利用鄰接矩陣X2，借助復雜網絡專業分析軟件UCINET，計算出中國綜合運輸網絡的平均最短路徑長度L=2.498，中國綜合運輸網絡中不同中轉次數的數量分布見表2.

由表2可知，在中國綜合運輸網絡中97.4%的城市對之間的運輸活動僅需2次以內的中轉即可實現，反應出中國綜合運輸網絡具有較強的服務便捷性.

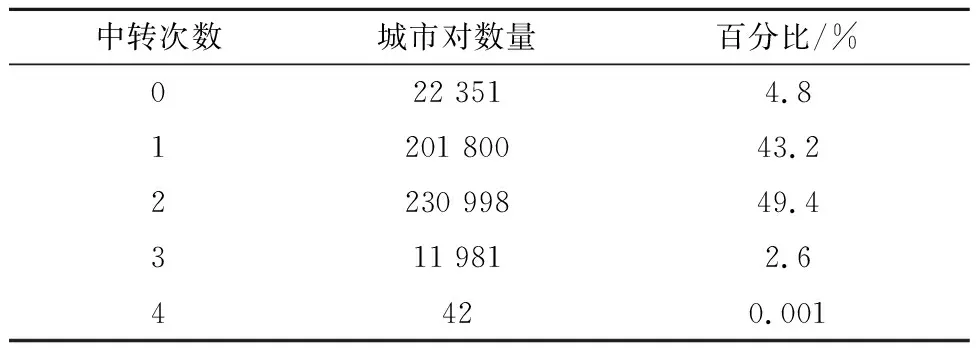
表2 不同中轉次數的城市對數量分布

2.4 中國綜合運輸網絡簇系數的實證研究

簇系數C是用于衡量網絡節點集聚情況的參數.節點i的簇系數是指：它的所有鄰節點之間連邊的數目占可能的最大連邊數目的比值[7].若假設網絡中的一個節點i有ki條邊將其和其他節點相連，顯然，在這ki個節點之間最多可能有ki(ki-1)/2條邊；而這ki個節點之間實際存在的邊數Ei和總的可能的邊數ki(ki-1)/2之比就定義為節點i的簇系數，見式(2).網絡的簇系數C則是所有節點簇系數ci的平均值.

Ci=2Ei/ki(ki-1)

(2)

簇系數代表節點城市與相鄰節點所構成的網絡的平均聚集程度，代表綜合運輸網絡的廣度[8].利用鄰接矩陣X2，借助復雜網絡專業分析軟件UCINET，計算出中國綜合運輸網絡的簇系數C=0.677，表現出很強的集聚性.

中國綜合運輸網絡具有小的平均路徑長度和大的簇系數，表明該網絡具有小世界網絡特征.也就是說，盡管中國綜合運輸網絡本身很大，但是在網絡中任意兩個節點之間存在相對較短的路徑.

2.5 中國綜合運輸網絡“介數及分布”的實證研究

一個節點的度值可以從一個角度反映出這個節點在所在網絡中的重要性，但是度值不能完全反映出某一個節點在網絡中所處的地位和扮演的角色.節點u的介數是指網絡中經過u的所有最短路徑的數量，見式(3).它反映了節點u對其他節點之間聯絡的控制作用[9].

(3)

式中：Sij為(i，j)之間最短路徑的集合.

在綜合運輸網絡中，一個節點城市的介數越大表明該城市中轉的能力越強，在綜合運輸網絡中的地位越重要.利用鄰接矩陣X2，借助復雜網絡專業分析軟件UCINET，計算出介數排名前30的城市見表3.

由表3可知，介數排名靠前的城市多為我國的省會城市，這些城市在“本省地級市與外省城市的連接”中發揮了重要作用.

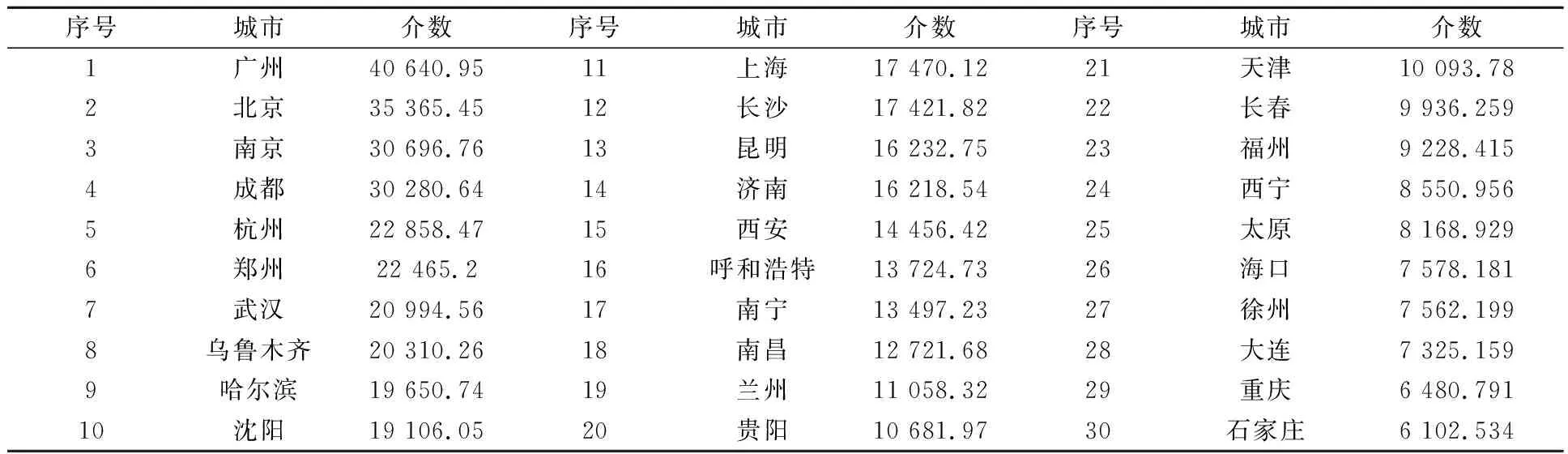
表3 中國綜合運輸網絡中介數排名前30位的節點城市

3 中國綜合運輸網絡的魯棒性分析

3.1 綜合運輸網絡魯棒性的內涵

綜合運輸網絡的魯棒性是指網絡對來自于外界的各種影響的阻抗性能.一般可以用網絡中部分節點城市陷入癱瘓后，綜合運輸網絡連通性來反映[10].如果某個節點城市因各類突發事件陷入癱瘓，意味在網絡中同時取消了與該節點城市相連的所有的線路，從而有可能使得綜合運輸網絡中其他節點城市從網絡中分離出去.如果在移走部分節點城市后綜合運輸網絡中絕大部分節點仍是連通的，那么就稱綜合運輸網絡的連通性對節點城市的故障具有較強的魯棒性.

在一定的連通性水平下，可取消的節點城市越多，綜合運輸網絡的魯棒性就越強；反之，則越差.魯棒性直接反映了綜合運輸網絡的穩定狀態以及對突發事件的兼容能力，是網絡整體性能的關鍵指標之一[11].

3.2 綜合運輸網絡魯棒性的度量指標

1) 連通魯棒性的度量指標 連通魯棒性是指網絡連通狀態對去除一定數量的癱瘓節點的阻抗程度.一般用“最大連通子圖的相對大小(s)”和“癱瘓節點數占綜合運輸網絡節點總數的比例f”的相對關系來反映.

“最大連通子圖”是指網絡中包含節點最多的連通圖.“最大連通子圖”越大表示網絡連通性越好，當“最大連通子圖”與網絡節點數相等時，表明網絡中所有節點間都是相互連通的.

“最大連通子圖的相對大小”的計算方法為[12]

(4)

當綜合運輸網絡受到外界干擾時，部分節點可能陷入癱瘓而失去原有的服務功能；隨著陷入癱瘓的節點的不斷增加，綜合運輸網絡中的“最大連通子圖”將不斷減小，甚至會形成數個孤立的子網絡.當一定時，s值越大，表明綜合運輸網絡的連通魯棒性越好.

2) 功能魯棒性的度量指標 功能魯棒性是指綜合運輸網絡的流通功能對去除一定數量的癱瘓節點的阻抗程度.經濟、便捷、快速的實現物資流通是綜合運輸網絡的基本功能,因此，可用“平均路徑長度l”作為綜合運輸網絡的功能魯棒性的度量指標.其中，“平均路徑長度l”平均路徑長度則是指網絡中所有節點對之間的最短線路數量的平均值.應用Ucinet軟件和鄰接矩陣X2，可計算出綜合運輸網絡的平均路徑長度為2.498，即在綜合運輸網絡中任意兩個節點平均只需要進行2.5次中轉即可到達.

3.3 中國綜合運輸網絡魯棒性的仿真系統設計

1) “隨機干擾型”仿真系統設計 “隨機干擾型”是指隨機的對綜合運輸網絡中的某個或某些節點進行干擾，使其陷入癱瘓狀態，喪失與其他節點間進行物資流通的能力，也就是意味著將該節點和其所有的邊從網絡中刪除.

“隨機干擾型”仿真系統的設計思路是：由于存儲綜合運輸網絡數據的鄰接矩陣X2的行和列中，節點城市都是按照一定的次序排列的，所以以隨機數的方式，確定鄰接矩陣X2的行和列受到影響的節點，并在矩陣X2中刪除該節點所有的邊，受到隨機干擾的綜合運輸網絡鄰接矩陣記為R.不斷重復上述步驟，直到網絡中癱瘓節點數量達到要求，該系統的基本流程見圖5.

2) “定向干擾型”仿真系統設計 “定向干擾型”是指有明確目標的對綜合運輸網絡中的某個或某些節點按照某一次序進行干擾.

“定向干擾型”仿真系統的設計思路是：以節點的“度”或“介數”值的大小次序，作為對網絡中節點進行定向干擾的次序.即根據節點“度”或“介數”值大小次序，逐個選擇節點城市進行干擾，受到定向干擾的綜合運輸網絡鄰接矩陣記為Y，重復上述步驟，直到網絡中癱瘓的節點數量達到要求，該系統的基本流程見圖6.

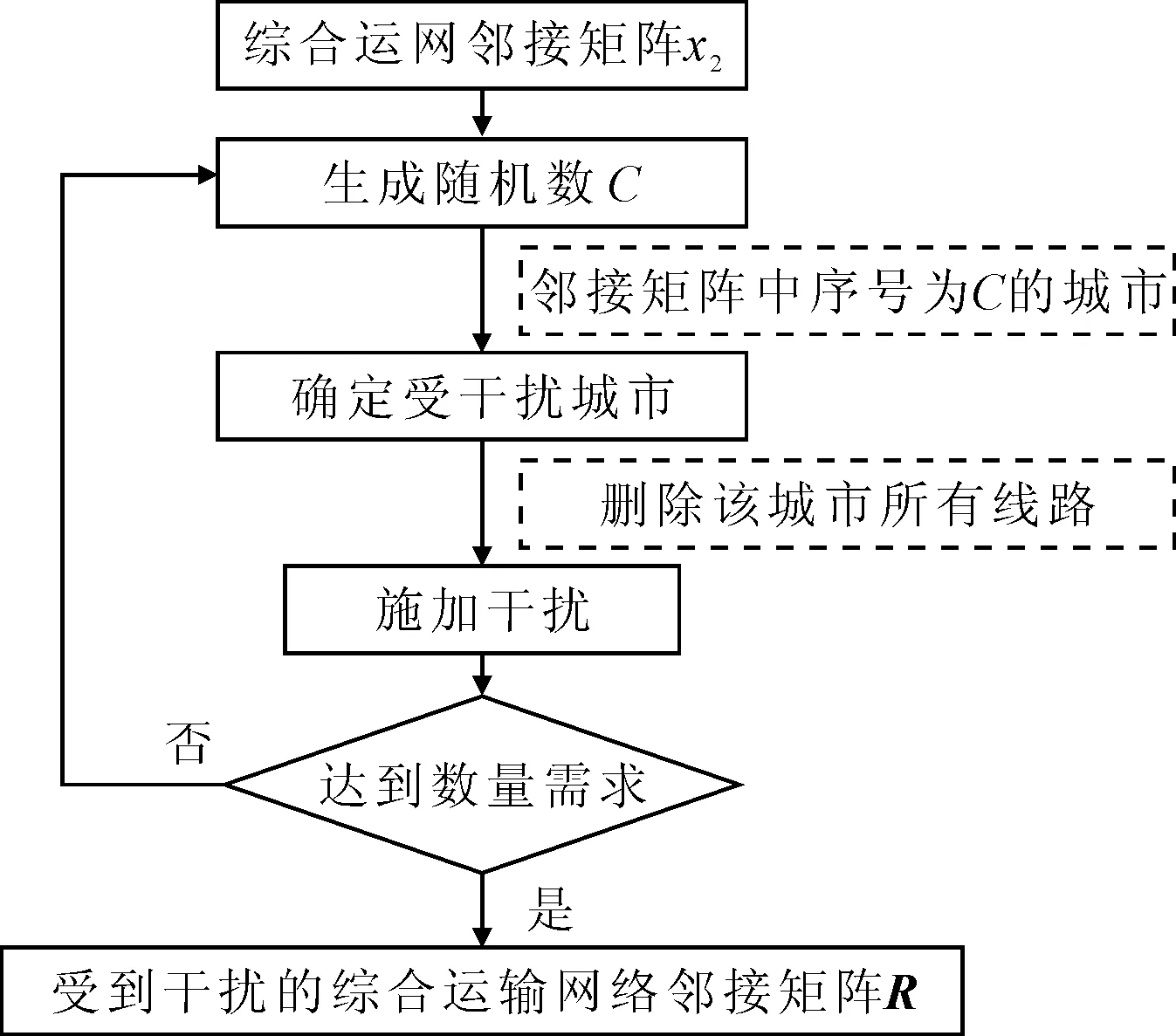
圖5 “隨機干擾型”仿真系統流程圖

圖6 “定向干擾型”仿真系統流程圖

3.4 中國綜合運輸網絡的魯棒性分析

1)f與s的對應關系分析 分別采用“隨機干擾”和“定向干擾”兩個仿真系統，計算684次干擾后對應的f和s值，其對應關系見圖7.

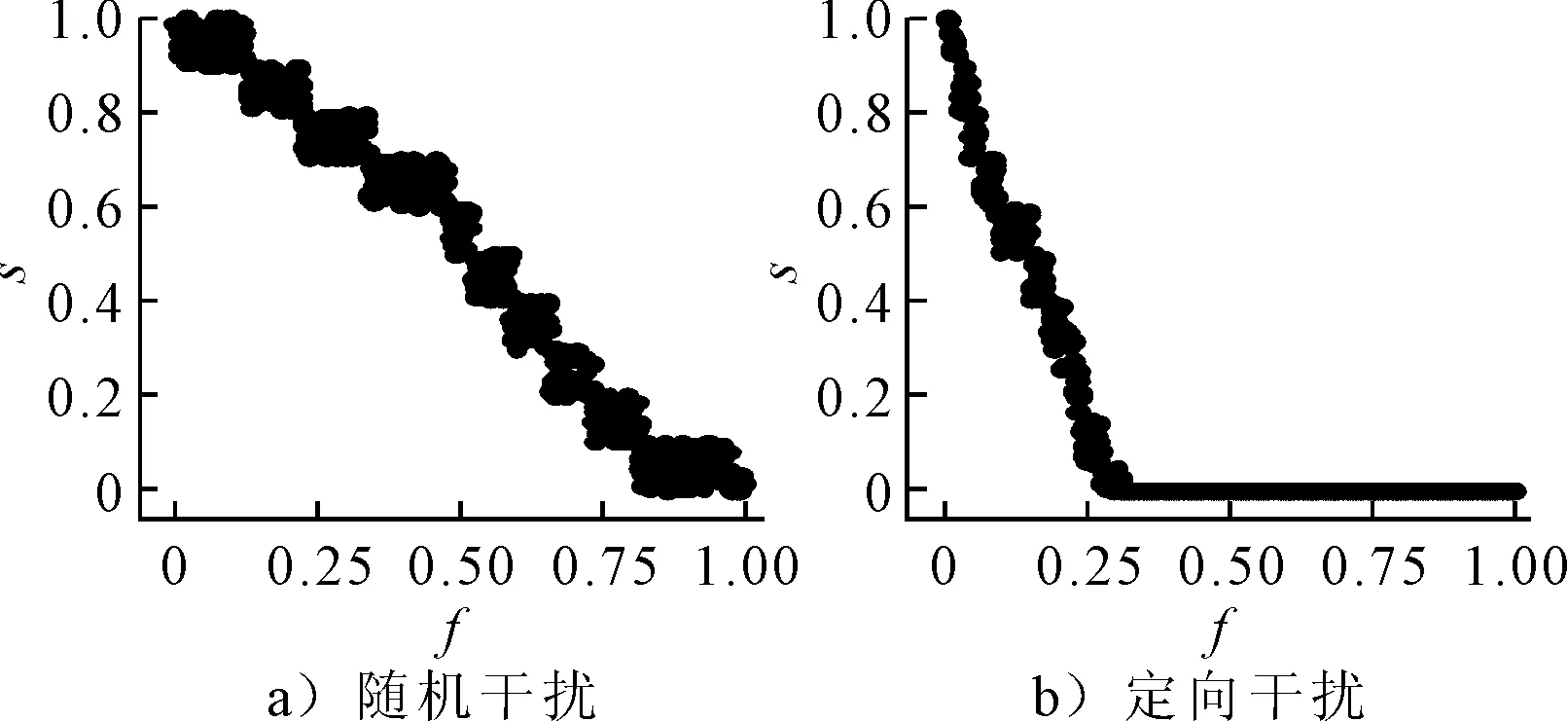
圖7 兩種干擾模式下f與s的對應關系圖

由圖7可知，在“定向干擾”系統中下降的速度明顯快于“隨機干擾”系統；若按照度值次序進行依次干擾，當大約30%的節點陷入癱瘓后，網絡便完全喪失服務功能.進一步說明：當節點因各類突發、偶發事故隨機陷入癱瘓時，綜合運輸網絡具有較強的魯棒性，而有針對性的進行定向干擾，將對綜合運輸網絡造成較大的影響.

2)f與l的對應關系分析 在“隨機干擾”和“定向干擾”兩個仿真系統，經過684次仿真干擾，f與l的對應關系見圖8.

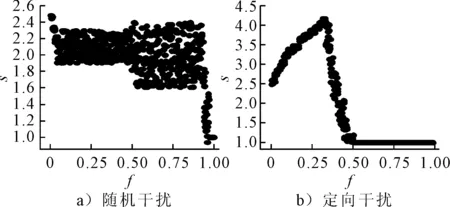
圖8 兩種干擾模式下f與l的對應關系圖

平均路徑長度l反映的是綜合運輸網絡中任意兩個節點城市間進行物資調運的中轉次數.由圖8可知，在“隨機干擾”和“定向干擾”兩種模式下，f與l的對應關系呈現出巨大差異.

在“隨機干擾”模式下，l值隨陷入癱瘓的節點的增加，在開始呈現出震蕩形式，并且震蕩幅度不斷加大；這表明隨機干擾并未對綜合運輸網絡物資調運的便利程度造成顯著的影響.在最終階段l降為1.這是因為隨著受干擾的節點不斷增加，網絡中相連的節點數量不斷減少，當所有節點都彼此孤立時，l值為1.

在“定向干擾模式”下，l值呈現出先快速增加后迅速下降的趨勢.表明對綜合運網的便利性影響顯著，后期快速下降的原因是由于網絡功能的快速喪失造成的，也就是說在“定向干擾”模式下，當受到定向干擾的節點達到節點總數的35%左右的時候，網絡的功能就受到了較大的影響；而“隨機干擾”模式下，這一比例大約是84%左右.

通過兩種模式的仿真實驗表明：節點的度和介數是影響綜合運網魯棒性的重要因素；綜合運網無論是網絡的聯通性還是網絡功能都體現出對隨機干擾的較強魯棒性，也就是說各種隨機發生突發、偶發類事故不會對綜合運網整體造成太大的影響；但是綜合運網針對定向干擾的魯棒性較差，應針對關鍵節點采取適當的預防與管理措施，以保證綜合運網的可靠性.

4 結 論

1) 從網絡節點的度分布上看，中國綜合運輸網絡三種鄰接矩陣的其網絡結構特征均表現出顯著的無標度網絡特征，其冪律系數介于[0.7，1.5]之間.

2) 中國綜合運輸網絡具有小的平均路徑長度和大的簇系數，表明該網絡具有小世界網絡特征；即在網絡中任意兩個節點之間存在相對較短的路徑.

3) 網絡中節點的“介數”與“度”值的大小存在加強的關聯性，我國的省會城市的介數值普遍較大，反應了這些城市在“本省地級市與外省城市的連接”中發揮了重要作用.

4) 節點的度和介數是影響綜合運網魯棒性的重要因素；綜合運網針對隨機干擾的較強魯棒性，但對定向干擾的魯棒性較差.