基于無跡卡爾曼濾波的巡飛彈氣動參數在線辨識方法

涂海峰 賈生偉 陽豐俊 呂 瑞

中國運載火箭技術研究院，北京100076

系統辨識是建立模型、改進模型以及驗證仿真模型精度的重要手段[1]。依靠系統辨識，僅通過飛行試驗中的輸入輸出觀測信息就可獲取系統的模型，其優勢尤其體現在飛行器平臺的開發上[1-5]。系統辨識可以代替風洞試驗獲取飛行器系統的氣動參數，縮短設計周期，降低設計成本，因而被廣泛應用于飛行器系統仿真平臺搭建和控制器設計。對于追求低成本的巡飛彈藥來說，如何通過系統辨識來獲取巡飛彈藥的氣動參數，以減少研發成本，縮短研發周期是值得探索的問題。

經過多年的發展，已經發展出多種常用的系統辨識算法，按照參數獲取的時間可分為離線辨識法和在線辨識法。其中，在線辨識法可以在線實時地估計模型參數，用于控制系統模型或參數在線修訂，因而比離線辨識法得到了更為普遍的應用。在線辨識算法中擴展卡爾曼濾波(EKF)辨識算法是使用較多的方法。1971年，Chen、Eulrich等人[6]在研究報告中將EKF辨識方法應用于某垂直起降飛機的控制導數和穩定導數的辨識。之后的若干年中，Jategaonkar、Walker、Speyer和Chowdary等人[7-11]進一步研究了EKF辨識方法在飛行器氣動參數估計中的應用。

雖然，EKF是目前針對非線性系統應用最為廣泛的狀態估計算法，但是它存在計算量大、估計精度低等缺陷[12-13]，同時部分復雜非線性系統很難求得系統的Jacobian矩陣和Hessian矩陣。為了避免這些問題，本文采用無跡卡爾曼濾波(UKF)實現飛行器的氣動參數估計，并將該方法應用于巡飛彈藥氣動參數估計，通過與EKF氣動參數辨識結果的對比分析，可知UKF在氣動參數辨識方面優于EKF，實現氣動參數的在線估計。

1 無跡卡爾曼濾波

UKF核心是通過一種非線性變換——無跡變換來進行非線性模型的狀態與誤差協方差的遞推和更新。對于非線性問題，相比EKF，UKF至少為二階近似，而且避免了計算系統的Jacobian矩陣和Hessian矩陣，拓展了適用于非線性系統的范圍。

無跡變換(Unscented Tranformation，UT)是UKF算法的重要環節，其基本原理為：在原先狀態分布中按某一規則取一些確定性的點集，稱為Sigma點，來表征輸入分布或部分統計特性，即使這些點的均值和協方差等于原狀態分布的均值和協方差；參數化的采樣點通過非線性變換進行傳播，利用變換后變量的均值和協方差近似采樣空間的均值和協方差[14]。因此UKF和EKF的區別如圖1所示。

圖1 實際采樣、EKF近似與UKF近似的區別

(1)

(2)

(3)

2 巡飛彈藥氣動參數辨識模型

飛行器的氣動參數辨識過程中，為了便于分析，一般將縱向和側向相關的氣動參數分開辨識。縱向和側向氣動參數辨識所采用的方法相同，這里只對巡飛彈藥縱向模型的氣動參數進行辨識。當巡飛彈藥在鉛垂面運動時，便可得到辨識所用的巡飛彈藥縱向非線性模型為：

(4)

式中,升力、阻力、俯仰力矩與攻角的計算公式如下：

(5)

D=CDQSw=QSw(CD0+CDosw(α-CDmin)2)

(6)

(7)

(8)

假設在飛行過程中沒有風的干擾，則可用式(8)來計算攻角。另外，式(6)存在2階項，對于最小二乘算法將是不可辨識的，需要對阻力系數的計算公式做如下變換：

D=CDQSw=QSw(CDα2α2+CDα1α+CDα0)

(9)

由式(5)到(7)可知，需要辨識的氣動參數為CL0,CLα,CLδe,CLq,CDα2,CDα1,CDα0,Cm0,Cmα,Cmδe和Cmq共11個氣動參數，這些參數構成待辨識參數向量θ為：

(10)

以上得到了巡飛彈藥的縱向非線性模型，以及待辨識氣動參數。下面將詳述基于UKF的氣動參數具體辨識過程。

3 基于UKF的巡飛彈藥氣動參數辨識

卡爾曼濾波只能實現狀態的最優估計，要實現未知參數辨識，需要將待辨識的參數增廣到狀態向量中，有：

(11)

為了保證所有狀態可觀測性，其輸出方程為：

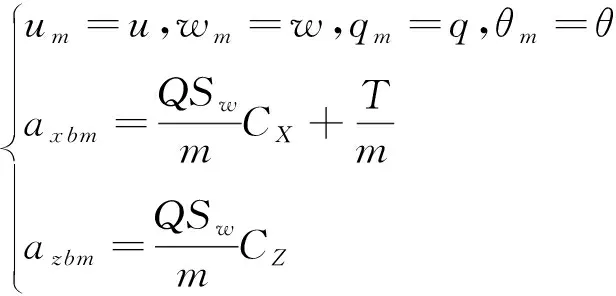
(12)

其中，CX和CZ分別表示在彈體坐標系下的氣動力系數，其計算公式如下：

1)輸入信號設計

為了實現參數的可辨識性需要設計控制輸入以充分地激發辨識對象的動力學特性。輸入信號設計的目的，就是設計飛行器執行機構的運動規律，使飛行試驗過程可以激發出與待辨識參數相關的運動模態，為辨識提供足夠的信息量。因此輸入信號應盡量包含多種頻率成分，滿足要求的常用的輸入信號有：階躍輸入、方波輸入、偶極方波輸入、“3211”多級方波輸入、振蕩型輸入和閉環控制輸入。

考慮到實際操作的簡便性，同時為保證輸入信息包含足夠的頻率以激發出縱向運動的所有模態，本文的輸入信號選擇為升降舵執行“3211”多級方波輸入，其數學模型為：

(13)

其中，Δt表示一個時間周期；δe0為平衡點處升降舵

輸入；Δδe為“3211”輸入的擾動量。為了充分地激發縱向運動短周期和長周期模態，升降舵采用如圖2所示的控制指令輸入，首先加入2個不同時間周期Δt不同擾動量Δδe的“3211”多級方波的信號，以激發短周期運動模態，然后加入一個周期較長的方波信號，以激發長周期運動模態。

2)辨識結果

將升降舵的信號輸入到巡飛彈藥六自由度非線性仿真平臺中，其它輸入如油門、方向舵和副翼則采用平衡點處的控制輸入。EKF和UKF待辨識氣動參數收斂情況如圖3所示，氣動參數的辨識結果如表1所示。

圖2 升降舵的輸入信號

圖3 Hybrid EKF和UKF待估計參數收斂圖

表1 參數辨識算法辨識結果對比

由圖3和表1的對比結果可以看出，EKF和UKF在有控制激勵輸入的情況下，兩者的收斂速度相當，然而對于阻力相關氣動參數CDα0，CDα1和CDα2的收斂結果來看，UKF明顯要比EKF算法更加接近于真值。因此可以得出對于在線辨識算法，UKF性能優于EKF。

4 結論

參數辨識能通過實際的飛行數據修正飛行器的氣動參數，使得仿真所用模型更加準確，本文研究在線參數估計算法，采用UKF實現對非線性系統的在線參數辨識，相比于EKF，其辨識精度要更高，同時避免了求解Jacobian矩陣和Hessian矩陣的問題。通過巡飛彈藥的仿真試驗，驗證了UKF在在線氣動參數估計領域優于EKF。