GPS在高鐵控制測量中的精度分析
——以西成高鐵為例

夏海寧，張帆宇揚，袁德寶，王 杰，龐世晨

(1. 廊坊市水利勘察規劃設計院,河北 廊坊 065000； 2. 中國礦業大學(北京)地球科學與測繪工程學院,北京 100083； 3. 滄州水利勘測設計院,河北 滄州 061000； 4. 廊坊市禹達勘測設計有限公司,河北 廊坊 065000)

隨著我國高鐵技術的不斷成熟[1]，越來越多的城市間依靠高鐵變的緊密起來，但西安與成都之間由于地形地貌復雜，給西城高鐵的建設帶來了很大挑戰。與其他高鐵線路相比，西成高鐵需要穿越秦嶺和大巴山區等地質地貌條件極為復雜的區域。線路主要由橋梁和隧道連接，超過10 km的特長隧道共有7座，最長的秦嶺天華山雙線隧道，距離超過15 km[2]，路線中隧道較多，其中密集隧道群長度達到了110 km，在工程西段、漢中境內和秦嶺山區的橋隧比分別高達92.1%、95%、94%，可以說整條高鐵線基本上是靠橋梁和隧道連接起來的。同時西成高鐵首次采用長達47 km、25‰的大坡度設計[3]，如此長距離、大跨度的橋隧工程線路是我國最具山區特點的高標準現代化高鐵建設項目，因此如何在險峻復雜山區為修建高速鐵路進行高精度的控制測量是保證高鐵順利建設的關鍵性問題。

1 高鐵控制測量

1.1 試驗區介紹

本文試驗區選擇在整條西成高鐵[4]中地質地貌復雜、具有代表性，且為全線設計建設的難點和重點區域的陜西境內的西安至陜川縣標段，技術設計書要求分CP0、CPⅠ和CPⅡ三級進行布設，CPⅠ網采用CP0點成果進行約束，CPⅡ網采用CPⅠ點成果進行約束，起訖里程為DK0+000～DK343+900，沿設計線路兩側帶狀分布，實際可用CPⅠ點8個。本次復測工作對CPⅠ級控制點采用同級校檢，由于CP點沿設計線路帶狀分布，為加強三角網網型強度，提高解算數據精度，需在遠離線路的合適位置架設輔助點。

1.2 控制測量的意義

由于西成高鐵施工測量環境復雜，受限于觀測條件，測量時不可避免地會產生誤差，因此需要在合適的地質地貌區域選擇穩固的點作為控制點。若干個控制點構成符合幾何條件的控制網型，作為西成高鐵在西安至陜川縣標段測區測量的骨架，控制累積誤差到限差范圍內。由于不同網型結構的測量精度、穩定性及成本不同，因此設計出合適的網型至關重要。

1.3 數據來源及質量

本文選擇西成高鐵CPⅠ點復測5月7日同步觀測數據進行GNSS網型布網設計分析。

外業觀測時，選取8臺雙頻Trimble GPS接收機，該款雙頻接收機具有優于5 mm+2×10-6D等級的靜態定位標稱精度。嚴格按照《全球定位系統(GPS)測量規范》(GB/T 18314—2009)中E級網規范，針對CP點的復測要求，外業觀測時段定為2 h，保持開關機同步、同步觀測同一衛星組。

西安至陜川界共分為10個投影帶[5-7]，本次試驗復測的CP點采用平面坐標系統，按高斯投影的方法建立工程獨立坐標系，投影分帶以按照對應的西成高鐵路線每千米平均高程變形值小于或等于10 mm的標準進行設計。

2 基線向量設計及解算

2.1 GNSS基線向量網的設計原則

衛星間同步測量不要求通視[8]，其測量得到的點位精度與所布設的幾何網型有很大關系。GNSS網的圖形設計[9-11]需要在考慮工程項目需求、成本預算、施工時長、GNSS接收機類型等條件的同時，也要保證測站點交通便利、有足夠的重復設站數等。

2.2 GPS網基線向量的解算

GPS網基線向量采用三差模型法求解，三差是不同歷元同一組衛星的雙差之差，三差方程消除了模糊度參數，并且進一步削弱了衛星軌道誤差和大氣折射誤差。

2.2.1 三差法解算函數模型

利用三差法來解算函數，能夠消除衛星定位中的多數誤差影響因素，獲得更為精確穩定的測量結果。設測站1、2分別在t1、t2觀測歷元同步觀測了編號為p、q的衛星，根據雙差觀測方程求差，得三差模型

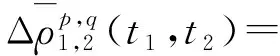
(1)

式中

2.2.2 三差法解算隨機模型

設某觀測歷元t1同步觀測衛星數為n，則可將基準站T1、測站T2至各衛星的非差相位觀測值先驗方差定義為

(2)

式中，a、b為常數；E為相應站點的衛星高度角。

假設不同衛星與測站之間的相位觀測值不具有相關性，同時歷元間的雙差觀測值不相關。因此可以通過誤差傳播定律[12]，在ti觀測歷元雙差相位觀測值的方差-協方差矩陣(式(3))的基礎上，獲得三差法解算的隨機模型(式(4))。

(3)

式中,⊙為克羅內克積；ln-1表示n-1維元素均為1的列向量；In-1為n-1階單位矩陣。

(4)

3 GPS網布設方案及布網特點

在本文試驗方案中，采用了以下4種網型設計進行分析試驗，其平差綜合情況見表1。

方案Ⅰ：全面網結構。所有測量的基線向量均參與網平差[13]，其布網方案如圖1所示。

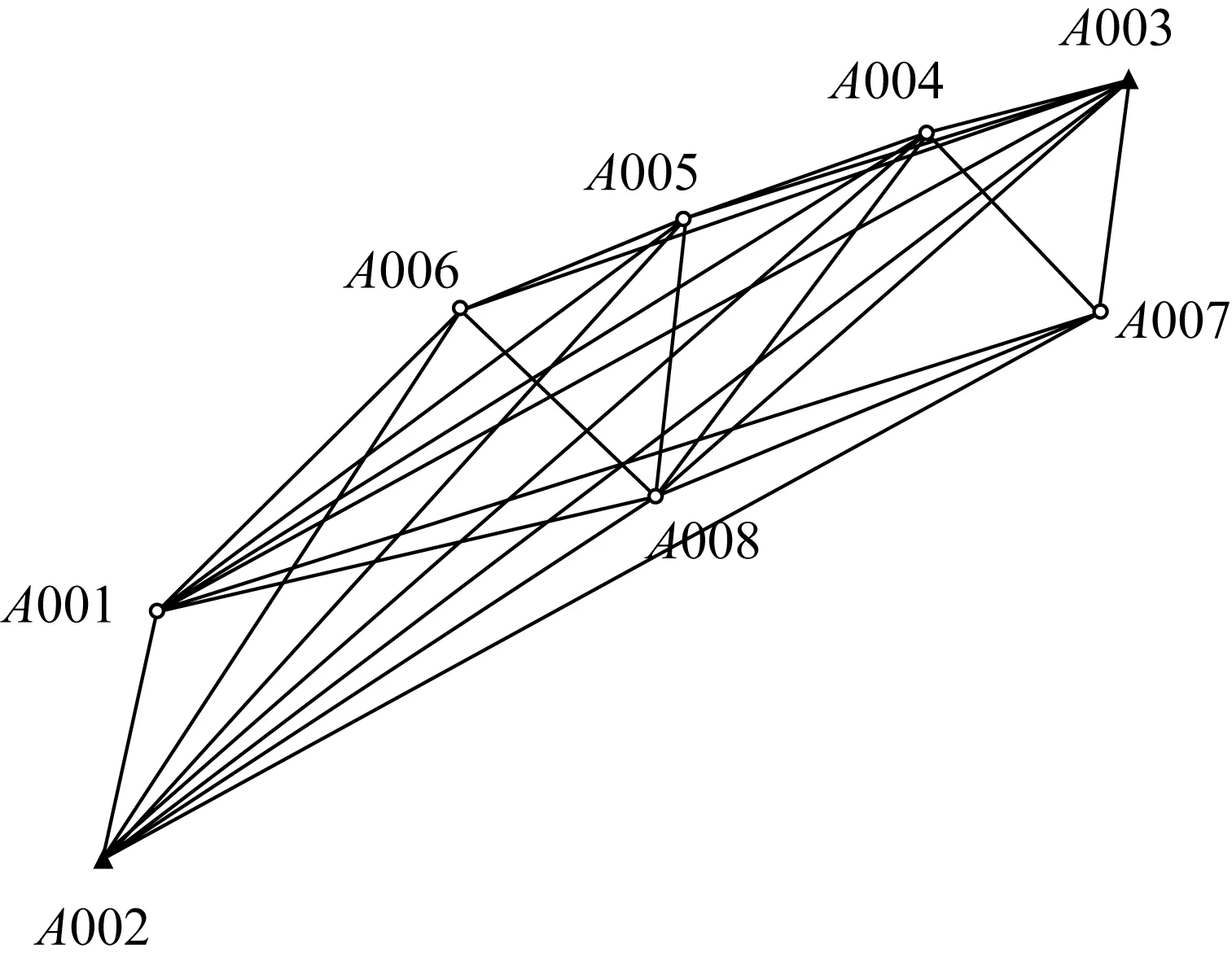
圖1 全網式示意圖

方案Ⅱ：邊連式結構。選擇部分基線向量參與網平差，依靠共用的基線相聯系。由于其有較多的復測邊和非同步圖形閉合條件[14-15]，故而在其余條件相同的情況下，該網型需觀測的時段數較另外3種網型有所增多，網型可靠性較高，其布網方案如圖2所示。

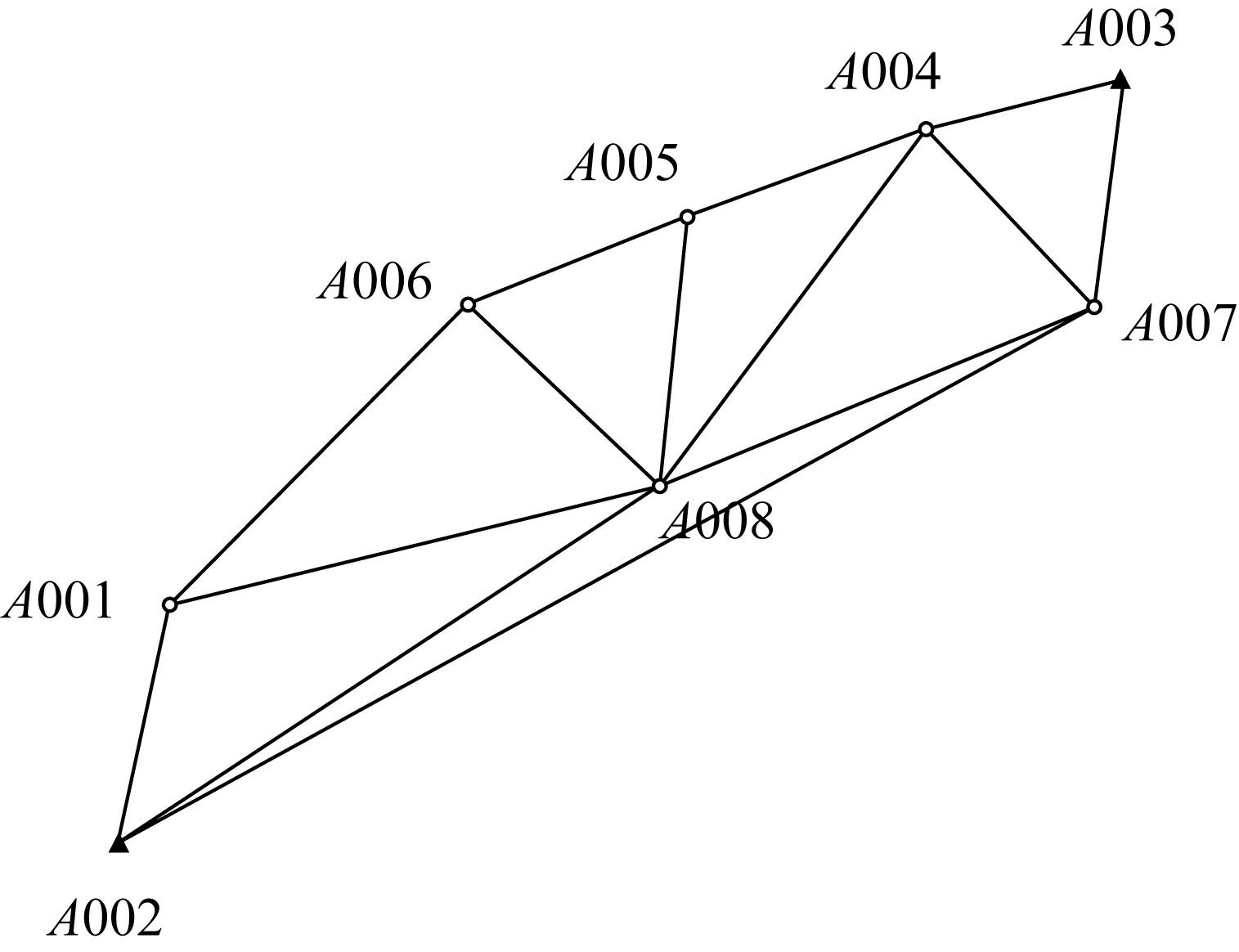
圖2 邊連式示意圖

方案Ⅲ：點連式結構。選擇部分基線向量參與網平差，只靠一個點連接，不具有較高的幾何強度，在工程實踐中也很少單獨使用，其布網方案如圖3所示。

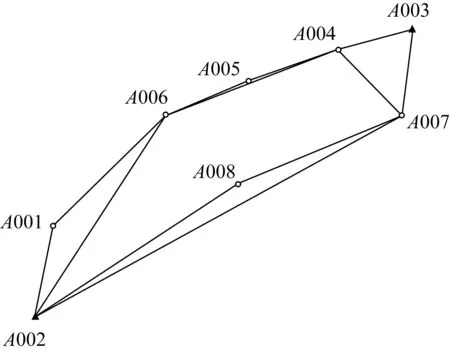
圖3 點連式示意圖

方案Ⅳ：導線網結構。根據實際情況，選擇部分基線向量參與網平差，利用邊連式與點連式兩種布網方式的特點，將兩者結合起來。該網型呈封閉狀，邊網混合使其不僅幾何強度較高，而且減少了外業工作量，在工程測量中有著較多的應用，其布網方案如圖4所示。

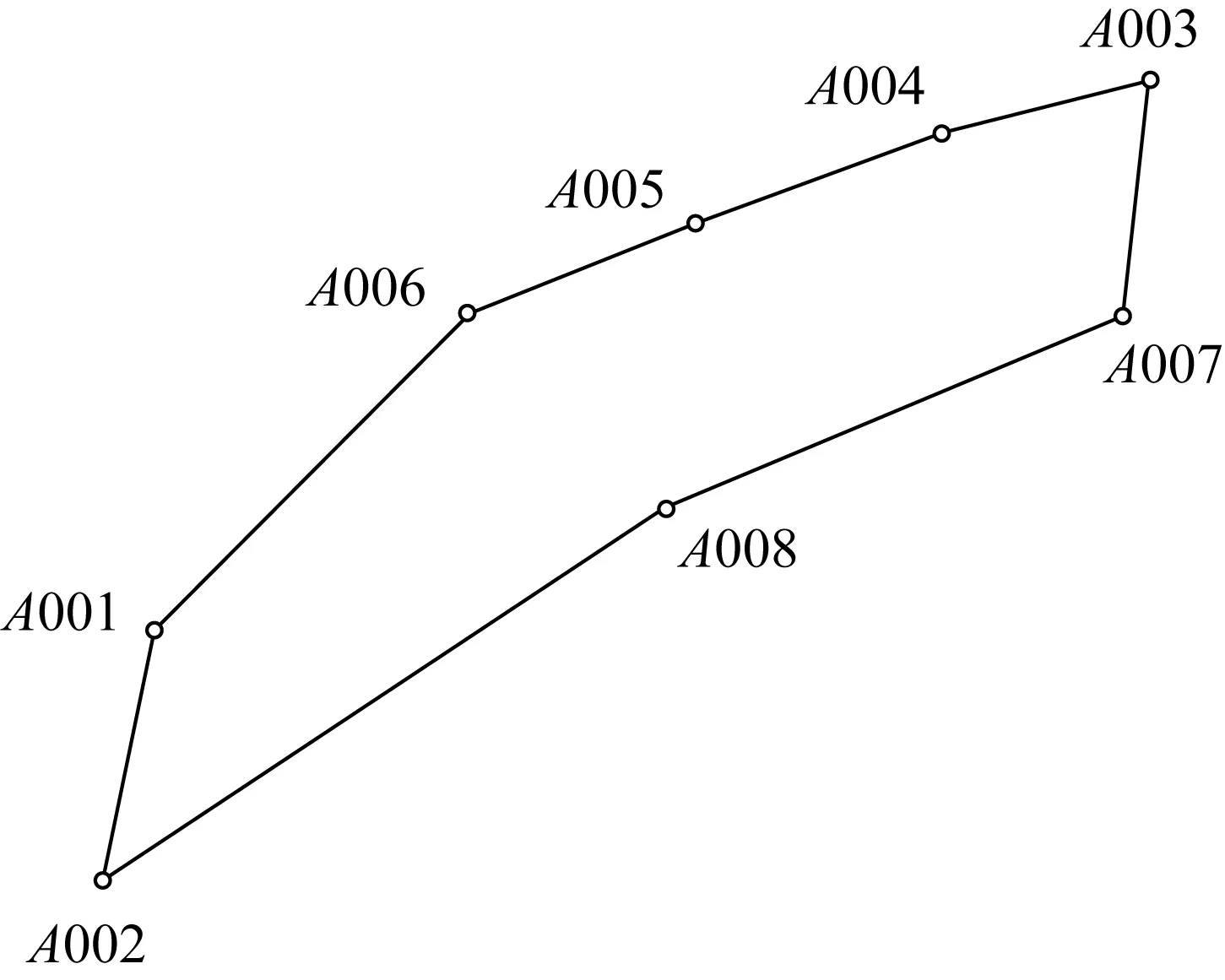
圖4 邊網式示意圖

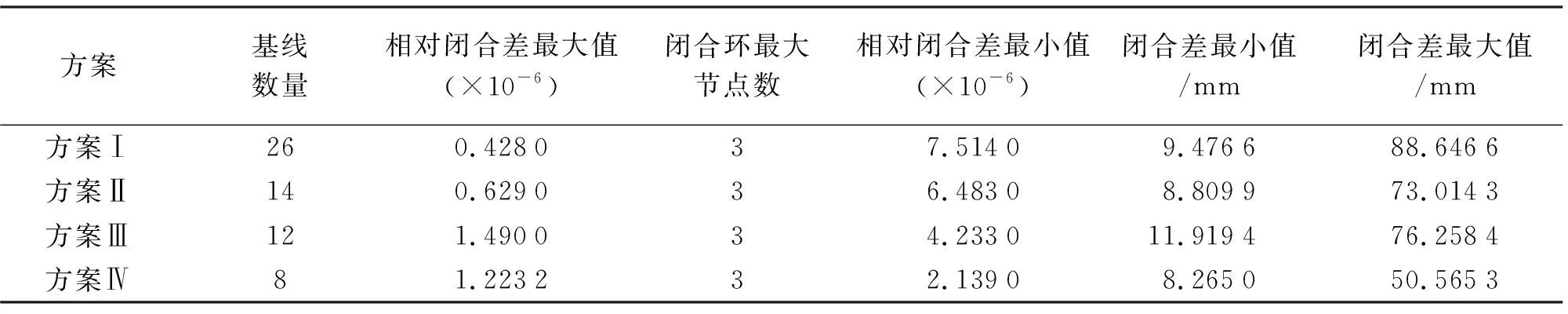
方案基線數量相對閉合差最大值(×10-6)閉合環最大節點數相對閉合差最小值(×10-6)閉合差最小值/mm閉合差最大值/mm方案Ⅰ260.428037.51409.476688.6466方案Ⅱ140.629036.48308.809973.0143方案Ⅲ121.490034.233011.919476.2584方案Ⅳ81.223232.13908.265050.5653

4 高鐵CPⅠ的復測結果分析

4.1 平面控制GPS測量精度指標及限差

(1)平面控制GPS測量的精度指標見表2。

(2)CPⅠ、CPⅡ復測的結果與相應的設計指標的坐標差值需滿足下列規定(見表3)。

此外，選取滿足要求的基線觀測值進行平差計算，由于國內測繪行業數據平差處理的規范標準要求，本試驗采用科傻平差軟件進行平差處理，觀測數據記錄和計算成果取位滿足相應的技術要求。

表2 GPS測量控制網的主要技術指標

表3 CPⅠ、CPⅡ控制點復測坐標較差及相對精度限差[18]

4.2 基線平差處理后的點位精度分析

以方案Ⅰ全面網的平差結果作為最或然值，將其他方案平差結果分別與方案Ⅰ的平差結果從水平方向進行點位坐標較差精度對比分析。

復測結果點位差值如圖5所示。

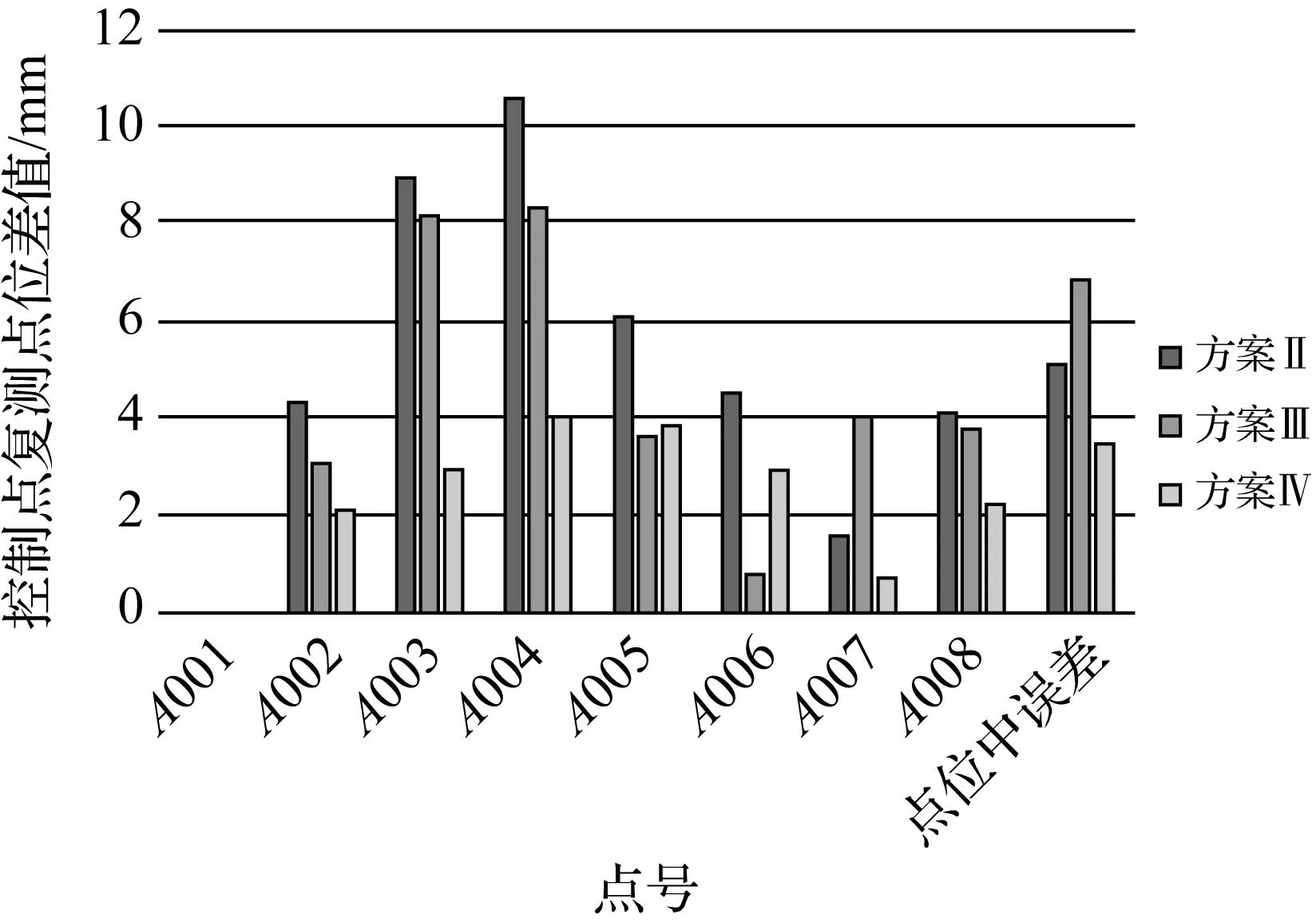
圖5 控制點復測點位差值

圖5中用到的計算公式有

(5)

式中，ds為點位差值。

(6)

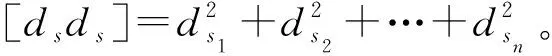
從圖5中可以看出，方案Ⅳ邊網式布網結構與方案Ⅰ全面網結構平差處理得到的點位坐標較為接近，方案Ⅱ邊連式布網結構解算得到的點位坐標與方案Ⅰ全面網結構之間較差在0.4～7.9 mm之間，而方案Ⅲ點連式布網結構得到的較差在0.3～6.2 mm之間。

相鄰點坐標差之差相對精度要求為1/130 000[19]，控制點復測坐標較差不超過20 mm。由以上數據分析可知，方案Ⅰ、Ⅱ、Ⅲ、Ⅳ均能夠滿足CPⅠ的精度要求。

4.3 基線平差處理的最弱點邊精度對比

由表4、表5可以看出，方案Ⅰ全面網的平差結果最優，方案Ⅳ導線網次之，方案Ⅱ邊線網與方案Ⅲ點連式的精度稍低，但以上4種布網方案均能夠滿足1/180 000的限差要求。

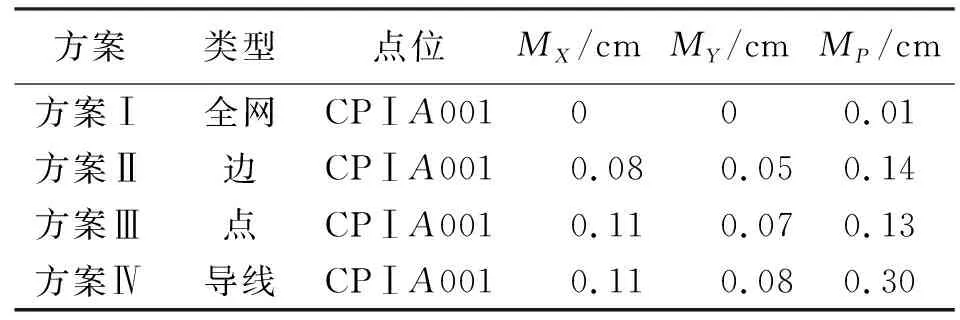
表4 平差處理后的最弱點精度

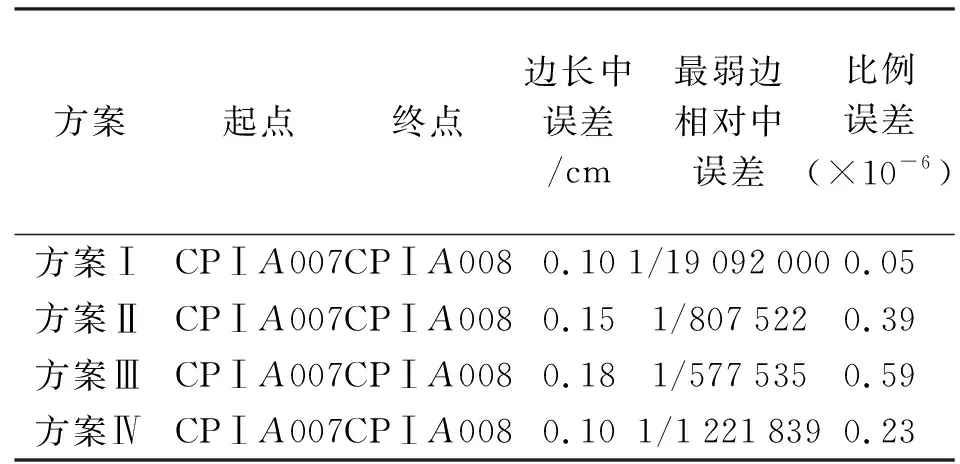
表5 平差處理后的最弱邊精度

5 結 語

本文以西城高鐵為例，利用GPS接收機所采集的數據，通過三差模型法對數據進行處理，分析了4種不同GNSS布網結構的CPⅠ控制點復測網平差解算成果，并采取多種不同的指標進行對比分析，可知GNSS網精度和可靠性的主要因素是基線向量的觀測精度。在小區域工程測量中，如果人員和儀器有限制，地質地貌環境不允許，可以考慮使用方案Ⅳ邊網式布網結構，適當減少重測點數，也能滿足精度要求，同時，在對采集到的數據進行內業處理時，可以剔除不滿足精度要求的基線，構成混連式布網構型或邊連式進項平差，以得到理想精度。