電熱法測熱功當量實驗數據處理方法
何建勛,唐 芳
(北京航空航天大學 a.能源與動力工程學院;b.物理科學與核能工程學院,北京 100191)
熱功當量實驗是驗證能量守恒和轉化定律的基礎實驗[1],其在裝置的設計、操作技能的訓練和數據處理方法的研究等方面都有助于對學生能力的培養[2],因此無論在物理學的發展還是在實驗教學中,熱功當量的測量實驗均具有較大的意義[2]. 目前實驗教學中普遍采用電熱法測量熱功當量,我校教材中該實驗的數據處理采用“差分代替微分”法求解熱功當量[3],這種方法只需記錄加熱升溫數據,但從我校實驗經驗上看,實驗所得的線性相關系數較低、且熱功當量測量誤差通常較大[4].
本文基于溫度補償原理和牛頓冷卻定律,對電熱法測量熱功當量實驗提出了2種散熱修正方法,即溫度補償法和線性回歸法. 首先簡單介紹電熱法測量熱功當量和2種新的散熱修正方法;然后對同一批數據用不同的方法處理并比較;最后針對線性回歸法,討論測點數目和測點時間間隔對實驗準確度的影響,給出實驗方案選擇建議.
1 電熱法測量熱功當量的基本原理
熱功當量可定義為傳熱量和做功量單位之間的數量關系[1]. 電熱法測量熱功當量實驗在量熱器中進行,用電阻加熱器向量熱器系統加熱,加熱過程中電流做功為
(1)
式中,U為加熱器兩端的電壓,R為加熱器的電阻,t為加熱時間. 在不考慮散熱的情況下,即假設電流做功全部轉化為熱量,使盛水的量熱器系統由初溫T0升到T,系統吸收的熱量為
Qab=(c0m0+c1m1+c2m2)(T-T0)=Cm(T-T0),
(2)
式中c0,c1,c2分別是水、量熱器和電阻加熱器的比熱容;m0,m1,m2分別為其相應的質量;Cm為系統的總熱容. 所以熱功當量J滿足:
(3)
即
如果各量均取國際單位,則熱功當量理論值J=1. 然而,即使實驗在量熱器中進行,系統和外界不可避免地會發生熱量交換,一般會根據牛頓冷卻定律進行散熱修正[3,5]. 當系統和環境溫差較小時,牛頓冷卻定律可表述為[6]:
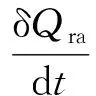
(4)
其中δQra為系統的散熱量,T和T∞分別為系統和環境的溫度,k為系統的散熱常量. 依據能量守恒關系,系統熱力學能增量等于其從加熱器的吸熱量與其和外界散熱量的代數和,綜合式(1),(3)和(4),系統溫度需滿足
(5)
式(5)為按照牛頓冷卻定律修正的熱功當量測量公式.
2 2種散熱修正方法的基本原理
2.1 溫度補償方法的原理
溫度補償法借鑒了測量冰的熔解熱實驗中廣泛使用的補償原理[2]. 在熱源供熱速率恒定且不大、系統導熱性能良好、攪拌充分均勻的條件下,系統的溫度變化過程可以認為是準靜態過程,即在任意時刻系統都處于平衡狀態[7],可以通過測量系統內一點的溫度來代替系統溫度.
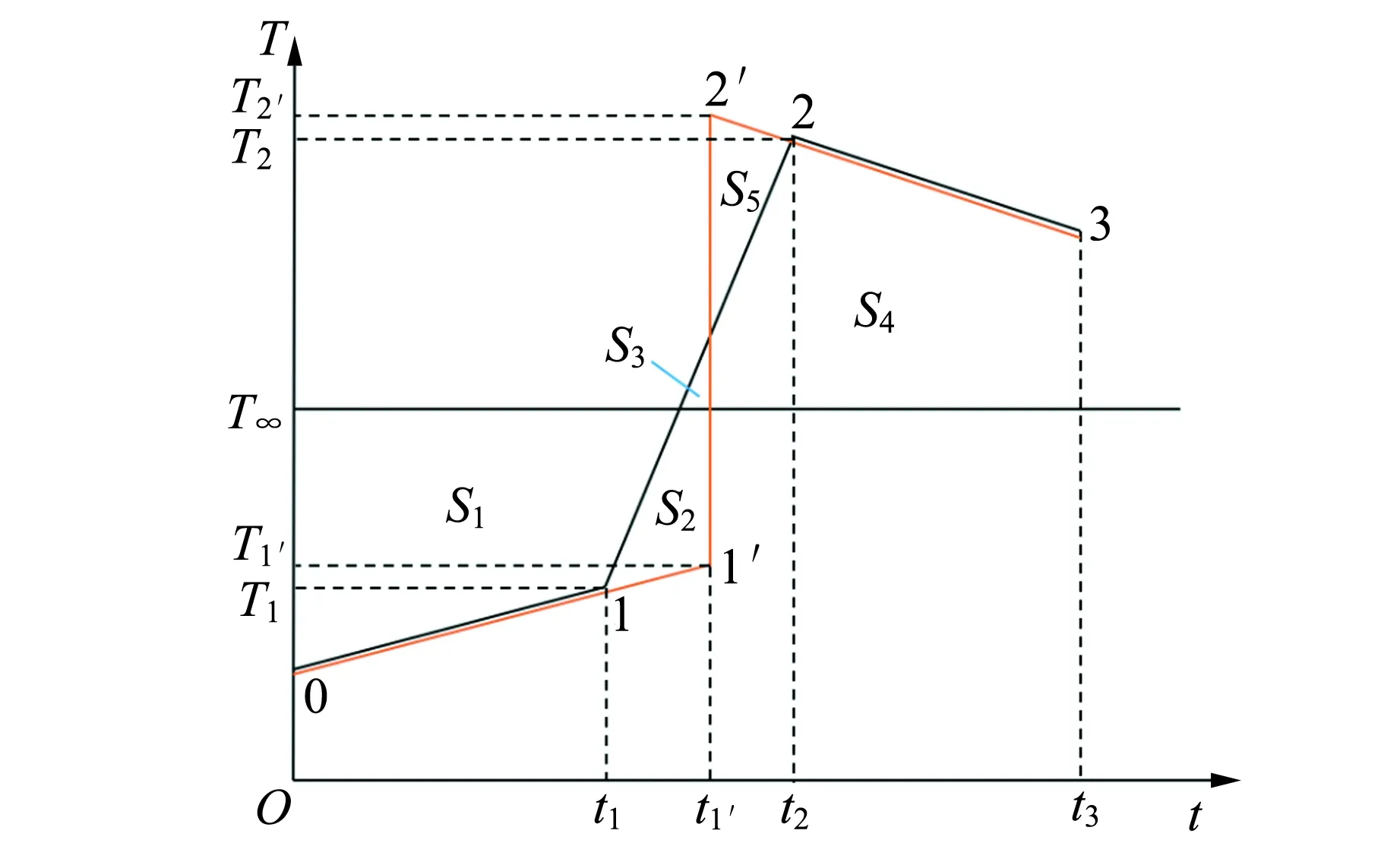
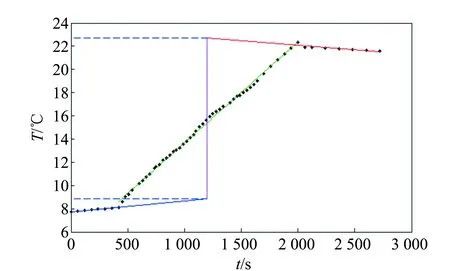
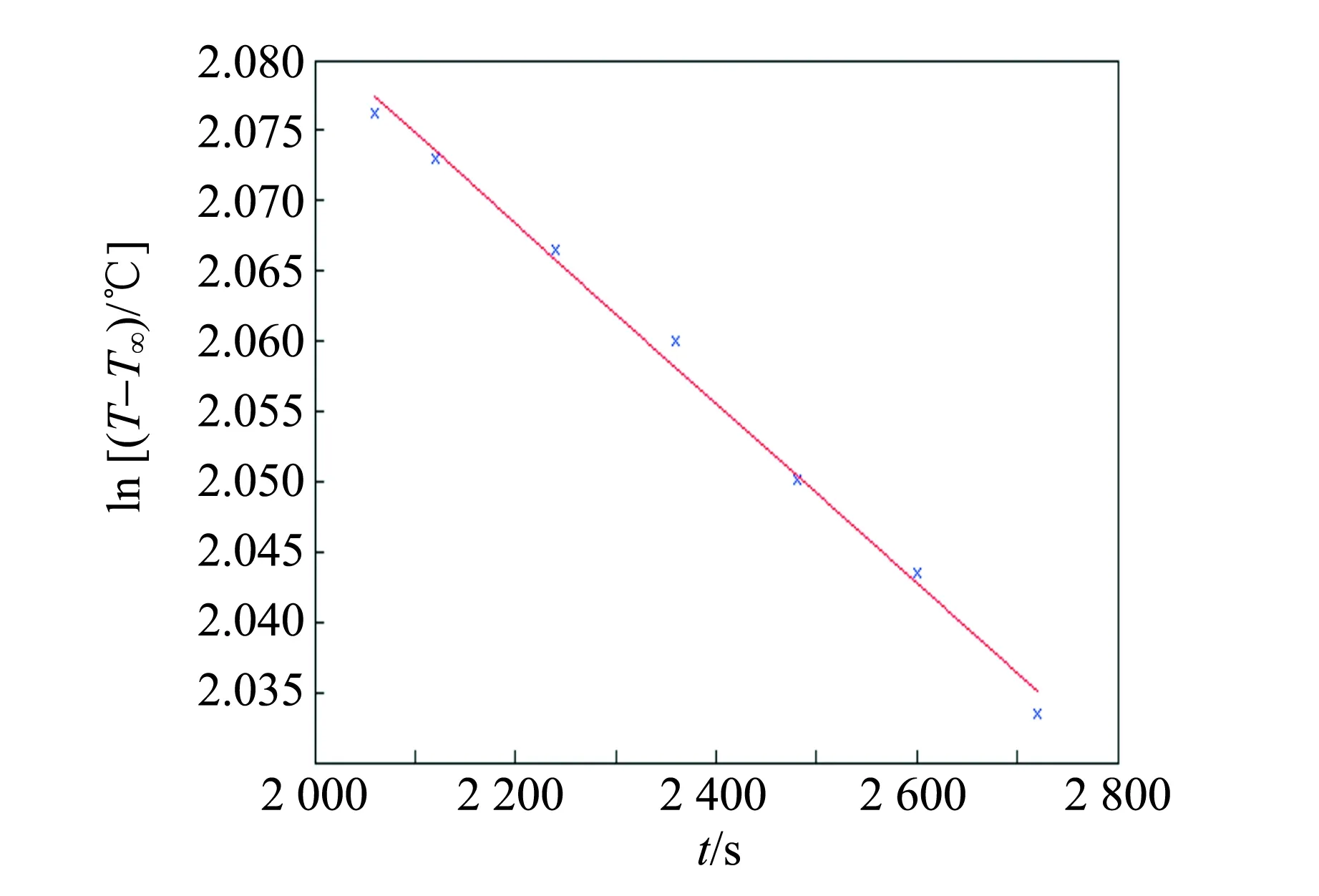
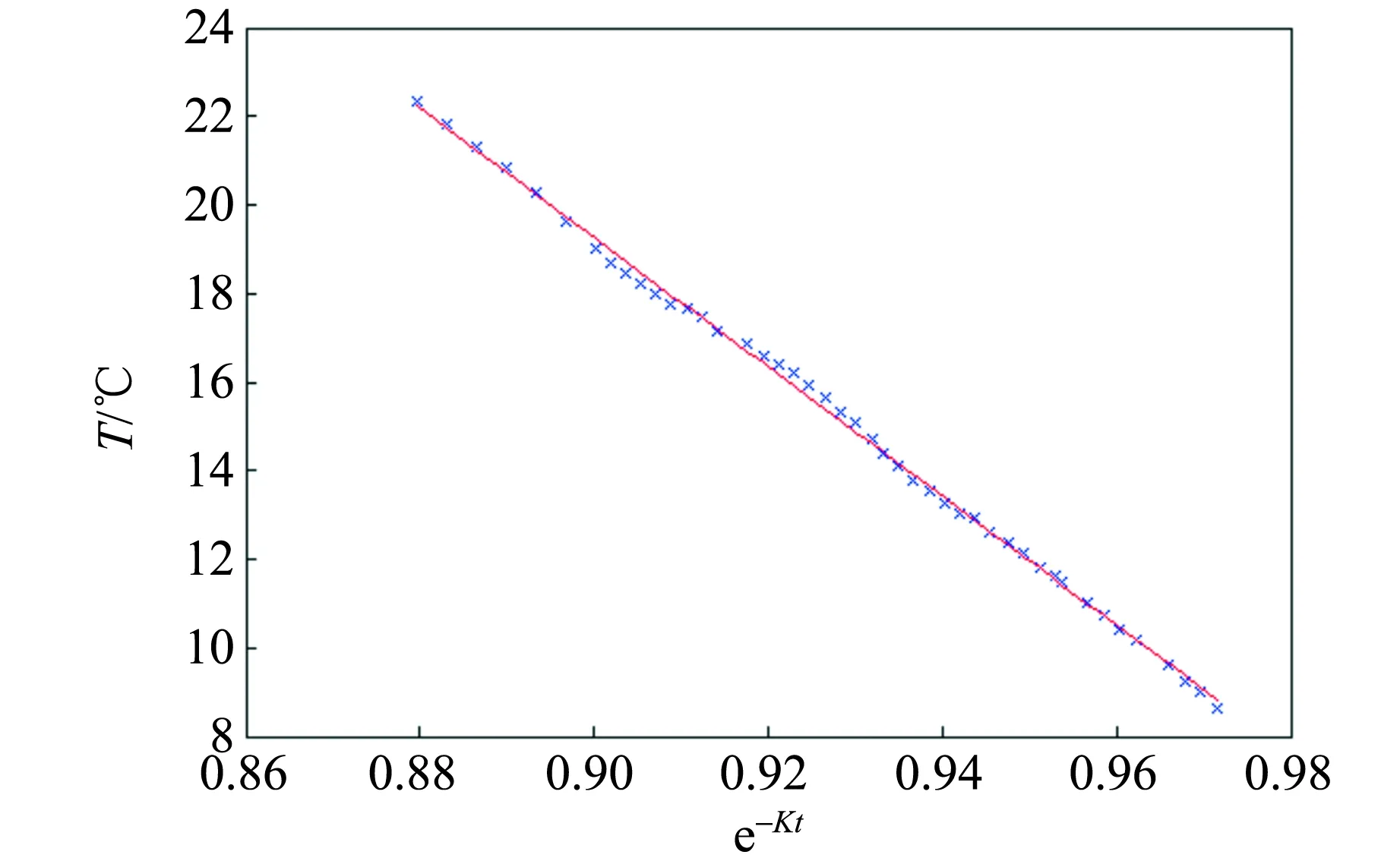
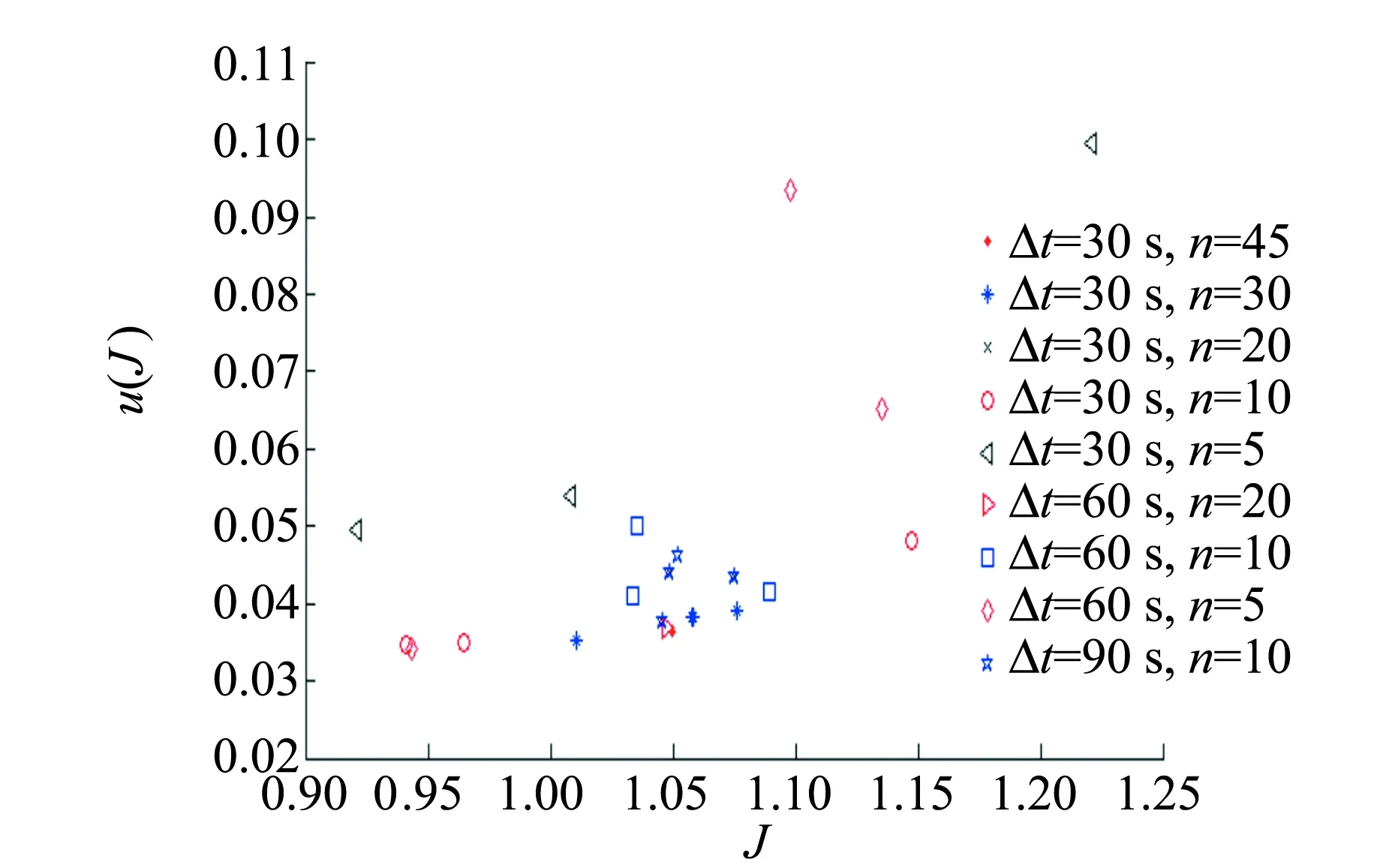
設實驗中系統溫度隨時間變化的大致趨勢如圖1中黑線所示,其中0-1段為加熱前的過程,由于此時各時刻系統溫度低于環境溫度,即T (6) 式(6)中等式左邊為全過程中系統的熱力學能增量,等式右邊第一項為系統對環境的散熱量δQra,第二項為系統從加熱器吸熱量δQab. 根據積分定義,等式右邊第一項可用系統的T-t圖像和T∞所圍面積的代數和表示. 若用圖1所示的面積定義,則: (7) 在T-t圖像上取一時刻t1′,過t1′作垂直于t軸的直線,并延長線段0-1和2-3,使得其與T-t圖像所圍面積S2,S3和S5滿足S2+S3=S5,則存在一假想加熱過程,系統溫度隨時間的變化如圖1中紅線所示. 其中0~t1′為加熱前的自然升溫,電加熱過程在t1′時刻瞬間完成,t1′~t3為加熱后自然降溫. 由于加熱過程在瞬間完成,所以系統與環境間的傳熱不發生在電加熱過程中,而僅發生在0~t1′、t1′~t3兩過程中. 在假想加熱過程中,系統和環境的傳熱可用圖1所示面積表示為 (8) 圖1 實驗溫度隨時間變化的趨勢和補償原理 由于作圖保證S2+S3=S5,由式(7)和(8),在圖1所示的0-1-2-3過程和0-1′-2′-3過程中,系統向環境間的散熱量相等,又因為系統的初末狀態相同(均為0狀態和3狀態),依據能量守恒關系,系統向外界的吸熱量等于初末狀態熱力學能的增量與系統向外界做功量之和[8],所以兩過程中系統從加熱器的吸熱量Qab相等,可以用0-1′-2′-3過程代替實際過程進行研究. 而且,因為在0-1-2-3和0-1′-2′-3過程中,僅有1-2段和1′-2′段存在從加熱器吸熱的過程,所以1-2段和1′-2′段的加熱量相等. 又因為1′-2′段的加熱過程無時間積累,不存在對環境的散熱,所以無論是0-1-2-3還是0-1′-2′-3過程,加熱量Qab均等于1′狀態和2′狀態熱力學能的差,即 (9) 在實驗數據處理時,延長2個散熱過程的溫度曲線,并在t軸上取t1′時刻,使得T-t圖像上的面積滿足S2+S3=S5,得到修正后的初末溫度T1′和T2′,代入式(9)即可計算熱功當量. 上述溫度補償方法可以修正實驗中的散熱,其原理清晰且計算量小,可行性強;但必須測量自然升溫和自然降溫過程,所以嘗試基于牛頓冷卻定律的二重線性回歸法. 由實驗條件可得,本實驗中系統和環境的換熱可近似看作大空間內的自然對流換熱. 由傳熱學實驗關系式[6],大空間自然對流換熱的散熱常數k與系統和環境間的溫度差ΔT有關,為 k=Cn(ΔT)n 其中n為由實驗確定的指數,操作中根據特征格拉曉夫數Gr的范圍而取不同的值,可取區間為(0.25,0.33),Cn為指前系數. 對本實驗對應的對流換熱條件,n取值應為0.33[6]. (10) 求解式(10)微分方程,可得加熱過程中溫度的變化為 (11) 同理可解得自然對流過程中溫度的變化 T=C2e-Kt+T∞, (12) 式(11)和(12)中的C1和C2均為積分常量,由初始條件確定. 對式(11)和(12)進行線性化變換,將式(12)移項并取對數得 ln (T-T∞)=-Kt+lnC2. (13) 令Y=ln (T-T∞),X=t,則式(13)滿足Y=-KX+c的形式. 所以在自然對流過程中對ln (T-T∞)和t做線性擬合,由擬合系數可求得K. 在加熱過程中令Y=T,X=e-Kt,則式(11)同樣滿足Y=aX+b的形式. 所以,在加熱過程中對T和e-Kt做線性擬合,由擬合結果可以計算熱功當量: (14) 而且,由于假設全過程中系統與環境的散熱常量保持不變,所以第二次擬合中的K值可用第一次擬合的結果代替,即第二次線性擬合和計算時的K值已知. 以下分別用溫度補償法和二重線性回歸法,對同一組實驗數據進行處理,并對處理結果進行比較. 取某次實驗測量結果,作出加熱前自然升溫過程、加熱過程和加熱后自然降溫過程中的T-t圖像,并對自然升溫和自然降溫過程做線性擬合,對加熱過程做多項式擬合. 可以得到,擬合相關系數均在0.99以上. 根據2.1節的溫度補償原理,做出類似圖1的假想過程,用紅線表示,即延長自然升溫和自然降溫過程,并使加熱升溫瞬間完成,如圖2所示. 圖2 某次實驗數據及其溫度補償結果 由溫度補償法可得出已修正的加熱初溫T1′和末溫T2′,代入式(9)即可求熱功當量. 修正后的加熱初末溫度分別是:T1′=8.81 ℃,T2′=22.34 ℃,求得熱功當量結果為J=1.03. 為方便比較,現選用與3.1節相同的測量數據,用二重線性回歸法進行處理. 全過程升溫范圍約13 ℃,散熱常數k在全過程中可看作常數. 根據自然降溫過程的T-t測量結果,對ln (T-T∞)和t做線性擬合,擬合結果如圖3所示. 圖3 自然降溫過程中ln (T-T∞)和t的線性擬合結果 擬合相關系數為r=-0.997 1,線性關系良好,由擬合斜率可以求得K=6.413 7×10-5. 假設全過程中K保持不變,在加熱過程中對T和e-Kt做線性擬合如圖4所示. 圖4 加熱升溫過程中T和e-Kt線性擬合結果 擬合相關系數r=-0.999 2,線性關系良好,理論推導與實際測量結果無明顯偏差,由擬合截距結合式(14)可計算熱功當量,計算結果為 J=1.049 7. 現考慮由此方法求得熱功當量的不確定度估計,測量結果的不確定度主要有儀器誤差造成的B類不確定度和由擬合誤差造成的A類不確定度. 相較于擬合誤差,溫度、時間、質量等測量的儀器誤差很小可忽略不計. 所以這里在進行不確定度合成,僅對擬合誤差造成的A類不確定度進行合成. 由第一次擬合關系式(12),結合回歸系數不確定度的計算方法可求得 (15) 同理由第二次擬合關系式(11)可求得 (16) 由式(15)和(16)結合式(14)以及不確定度的合成原則可求得 按照上述方法,本節算例中的不確定度u(J)計算結果為u(J)=0.036 2≈0.04,所以本算例熱功當量的最終表達為J=1.05±0.04. 2種方法均可對散熱進行修正,得出較準確的熱功當量結果,在原理和具體實踐中都是可行的. 相較而言,溫度補償方法借助圖形工具,將系統與環境的散熱量轉化為T-t圖像中的面積,省卻了復雜的散熱微分方程的求解,使數據處理更加直觀簡便. 二重線性回歸法可通過求解散熱常量恒定假設下的散熱微分方程,得出完整而嚴格的數據處理原理. 然而該方法處理過程相對較復雜計算量大. 并且實際過程中的散熱常量并非恒定,而是和系統與環境的溫度差有關[6],由此引入的近似也會帶來實驗誤差. 二重線性回歸方法可以得到完整嚴格的數據處理原理,但計算量過大的問題仍需解決. 理論上,在不影響結果準確度的前提下適當減少測量點的數目可以減少數據處理的工作量. 一般而言,在總時間不變的前提下增大相鄰測點的時間間隔Δt,或在時間間隔不變的情況下減少測點的數目n均可減少測量點的數目. 為討論這2種方法對準確度的影響,在相同條件下改變測點數目進行了多次實驗,圖5為加熱升溫階段測點間隔及測點數目同計算結果的關系對比. 圖5 加熱升溫測點間隔和測點數目對計算結果影響 總體而言,測點數目和相鄰測點的時間間隔對實驗結果存在影響. 加長實驗時間并密集測點有助于降低實驗結果的誤差,提高實驗結果的準確度. 然而過長的實驗時間將會增加實驗過程中環境因素的不確定性,不利于結果的準確. 由圖5可得,當Δt取為30 s時,在n≥20的情況下實驗結果的分布較密集,數據的重復性好;在n=10或5時,實驗結果分布則較分散,數據的穩定性欠佳,且出現了較大不確定度的情況,說明擬合相關性不好. 當Δt由30 s增加到60 s而n不變時,計算結果的重復性和準確度即可得到改善,說明在測點數量不變時,適當增加實驗的總時間,即增加相鄰測點的時間間隔可降低實驗結果的不確定性,使結果更穩定. 當Δt=60 s時,若n減小至5則同樣會出現結果分散,此時實驗結果的可信度低. 所以為了保證實驗結果的準確性,測點間的時間間隔不宜過小,一般不能小于60 s;測點數量不宜過少,一般不能小于10;當時間間隔加長至90 s時,測點數量也需為10. Δt和n的最佳取值分別為Δt=60,n=10. 基于牛頓冷卻定律,提出了2種對熱功當量實驗的數據處理方法,即溫度補償法和二重線性回歸法,二者均可降低散熱帶來的系統誤差,得到較準確的實驗結果. 溫度補償法不涉及復雜的數學推導,數據處理更加直觀和簡便;線性回歸方法來源于對散熱微分方程的求解,在數學上更加嚴格,且能給出實驗結果的不確定度估計. 為解決線性回歸方法數據處理工作量大的問題,可在保證實驗準確度的前提下適當減少實驗測點的數目,合適的Δt和n取值為:Δt=60,n=10. 使用此方法進行數據處理,可以明顯解決“差分代替微分求解散熱量”方法中線性相關系數低、誤差較大的問題,得到準確的結果.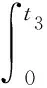

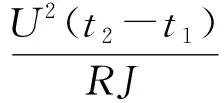
2.2 二重線性回歸方法的原理
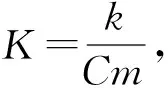
3 結果與討論
3.1 溫度補償法的處理結果
3.2 二重線性回歸法的處理結果
3.3 2種方法的比較
4 關于二重線性回歸方法的進一步討論
5 結束語

